峰回路转 天堑通途

许银伙

(福建省泉州外国语中学 362000)

(2)若存在不过原点的直线l使M为线段AB的中点，求p的最大值.

(2)设点A(x1,y1)(x1>0,y1>0)，B(x2,y2)，M(x0,y0)，由椭圆C1和抛物线C2的对称性得：直线l的斜率存在且不为0，设直线l方程：y=kx+m(k>0).

思考一联立椭圆C1和抛物线C2方程，可得点A关于参数p的坐标.联立直线l与椭圆C1方程，运用韦达定理可得点M(x0,y0)坐标.联立直线l与抛物线C2方程，运用韦达定理可得点A坐标，由点A是直线l椭圆C1和抛物线C2的公共点，得到p关于某个已知范围的未知数的关系式.

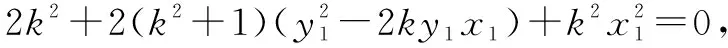
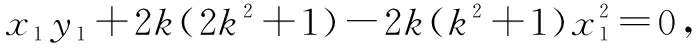
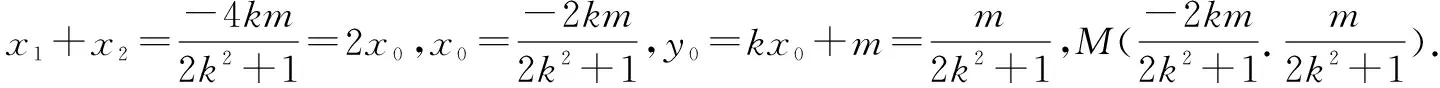
经过上面的分析和解答，可以体会到：入手思维层次的高低，极大影响解答的运算量.方法一属于浅层次分析，边摸索边解答，走了弯路；方法二是经过数理分析，借助参数方程的知识，摸索出了利用比例值减少参数量；方法三和四是利用方法二的结果进一步提升优化；方法五是在入手时提高思维的深度，简化解答难度.从方法二三四中，总结出普遍性的规律：凡是可化为关于某两个量的齐次方程，都可以考虑比值换元解决.本题还可以设直线l方程为x=my+t(m>0)，此时相应的方法五就是参考文[1]高考参考解答的思路.

解题能力的提升，需要磨炼，需要对问题充分的研究与探索，即使失败，即使走弯路.弯路可能成为风景，如上面利用比例值减元，失败和弯路都是进步的基石.正所谓：千淘万漉虽辛苦，吹尽狂沙始到金；美人首饰侯王印，都是沙中浪底来.