亚轨道飞行器返场技术研究

汪保旭，孙歌苹

(南京航空航天大学 飞行控制研究所，江苏 南京 210016)

0 引言

亚轨道飞行器(SRLV)是一种在亚轨道空间飞行、可重复使用的多用途飞行器。相比于轨道飞行器，亚轨道飞行器具有系统结构、发射条件简单、飞行成本低等特点，因而在军事和民营领域，亚轨道飞行器已经成为研究的热点。

根据不同的飞行任务，亚轨道飞行器在上升段与结束时状态差异巨大，高度的变化范围为30 km～70 km ,速度的变化范围为0.76 m/s～1.27 m/s。不同的初始返回状态对应不同的航程，制导系统需根据初始返回点的状态判断飞行器能否返回着陆场。

亚轨道飞行器返回阶段通常分为3个阶段：初期返回段、能量管理段和着陆段。X-34应急返场方案[1]可推算飞行器在能量管理段入口飞行状态，比较该状态下可飞行的航程以及到各个着陆场的待飞距离，选择合适的着陆场并返回。航天飞机的GRTLS(glide return to launch site)即滑翔返回发射场制导[2-3]是在上升飞行的前4 min内因发动机故障无法正常入轨，实施应急策略，使航天飞机进入能量管理段窗口，并最终返回预先设计的发射场。

由于亚轨道飞行器的初期返回段高度较高，空气稀薄，气压低，虽然待飞距离可以由横侧向制导算法计算出，但纵向无法规划高度和动压剖面，因而无法根据初期返回点的能量状态判断飞行器的航程能力，进而判断能否返场。

本文将初期返回段当作能量管理段的延伸，参考能量管理段的判断方法[4]，设计制导参数迭代算法，分别通过调整初期返回段的迎角指令、航向校准圆柱(heading align column, HAC)位置和切换进场方式来判断飞行器能否从最高点返回着陆场，最后进行实例仿真验证。

1 质点动力学方程

亚轨道飞行器初期返回段主要考虑纵向运动，忽略横侧向的影响。由于地球自转引起的哥氏力、重力加速度变化较小，假定重力加速度为常数，忽略地球曲率，忽略自转的影响，简化后的质点动力学方程为：

(1)

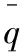
2 制导问题描述

根据不同的飞行任务，亚轨道飞行器从最高点返回时的状态不同。高度越高，速度越大，飞行器的能量越大，可飞行的航程越远，反之航程越近。因此，当初始返回点的位置、速度和高度确定时，制导系统就能够判断当前状态能否返回着陆场。

参考能量管理段的判断方法，速度一定时，由初始返回点到着陆场的待飞距离计算出高度指令。若当前高度小于高度指令，则飞行器到不了着陆场；若当前高度大于高度指令，则飞过着陆场。由上文知，无法单独根据初期返回点的能量状态判断飞行器的航程能力，进而判断能否返场。

初期返回段纵向制导采用的是跟踪开环迎角指令，调整迎角指令可以改变初期返回段结束时的高度。另一方面，由于初期返回段的航程受迎角指令变化影响较小，因而调整返回段的待飞距离主要影响能量管理段后面的飞行阶段。制导系统通过调整初期返回段的迎角指令和返回段的待飞距离来验证给定状态的飞行器能否返回着陆场。

3 迎角指令对高度的影响

在初期返回段，亚轨道飞行器的轨迹角为负，升力和阻力在纵向的分力竖直向上，平衡重力，从而降低垂直加速度，抑制下沉率[5]。下沉率的公式为：

(2)

式中V为空速。

(3)

式中：L为升力；D为阻力。

由于CL、CD是迎角α、马赫数Ma和气动舵面的函数，当马赫数和气动舵面一定时，迎角越大，CL、CD越大；升力越大，阻力越大，两者竖直向上的合力越大。从而垂直加速度越小，下沉率变化越小，初期返回段结束时高度越高；反之，迎角越小，初期返回段结束时高度越低。

同一初始返回状态，不同初始迎角条件下，图1是初期返回段的航程变化曲线，图2是下沉率变化曲线，图3是高度变化曲线。可知，初期返回段航程受迎角指令变化的影响较小，下沉率和高度影响较大。

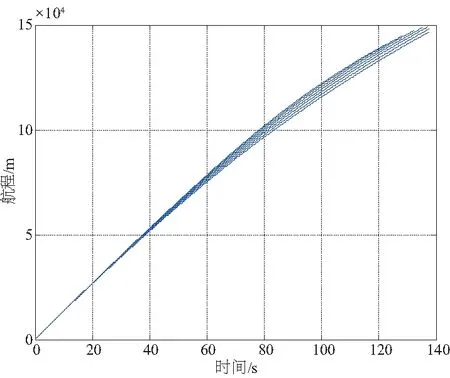
图1 初期返回段航程变化曲线

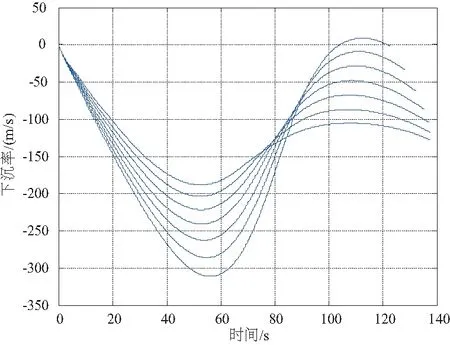
图2 初期返回段下沉率变化曲线

图3 初期返回段高度变化曲线

4 调整待飞距离的影响

当初期返回段的迎角指令调整到边界值时，再通过调整HAC位置和切换进场方式来改变整个返回段的待飞距离。

由第3节可知，初期返回段不同的迎角指令对航程影响不大，因而调整HAC的位置主要影响能量管理段后面的待飞距离。当初期返回段结束时，实际高度低于高度指令，将HAC调整到最小位置，减少待飞距离；反之，实际高度大于高度指令时，将进场方式由直接进场改为间接进场，增大待飞距离。由表1可知，HAC距离跑道越近，返回段的待飞距离越小，剩余的待飞距离越短，计算出的高度指令越低。图4是进场方式示意图，由图可知，间接进厂的待飞距离远，剩余飞行的距离多，计算出的高度指令高。

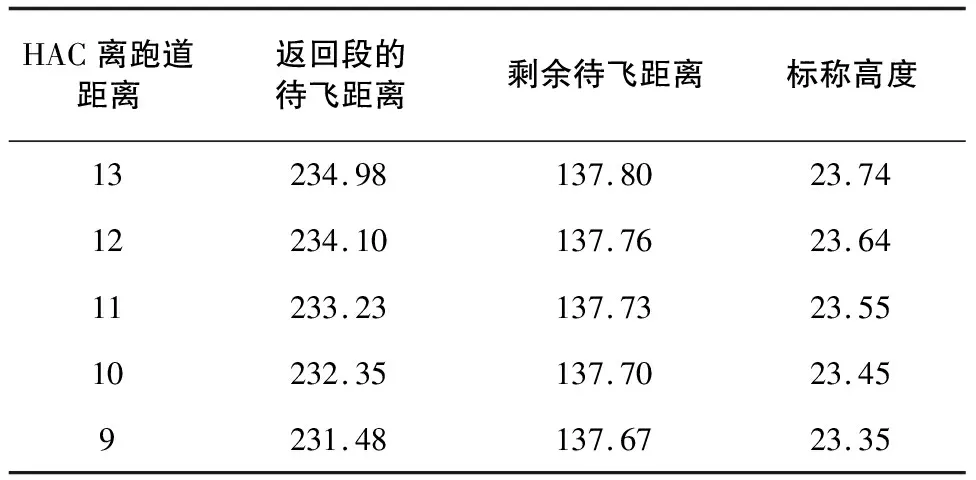
表1 初始返回点状态 单位：km

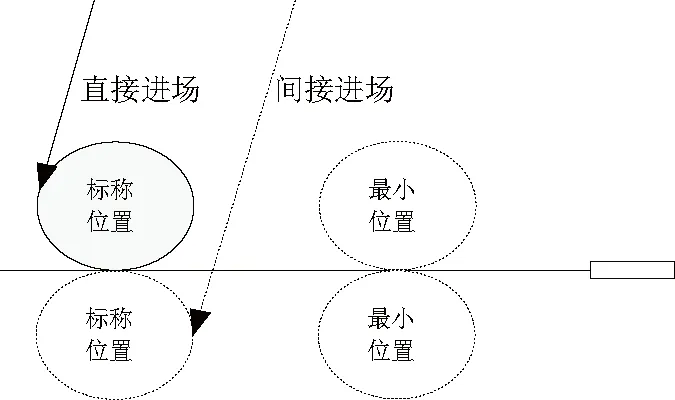
图4 进场方式以及HAC位置示意图

5 设计制导参数迭代算法

上文分别分析了RLV返回过程中，迎角指令对再入段结束时高度的影响以及调整HAC位置、切换进场方式对返回段待飞距离的影响。基于此，设计了制导参数迭代算法。

具体算法如下：任意给定一个初始返回状态，首先初始化HAC和着陆机场，制导系统计算出到着陆场的待飞距离，并根据初始速度计算出迎角指令，接着进行时间迭代。当初期返回段结束时，可以得到初期返回段的航程，用总的待飞距离减去初期返回段的航程得到剩余的待飞距离。再由剩余的待飞距离插值出标称高度指令，比较实际的高度和标称高度，判断能否返回着陆场。

当实际高度高于标称高度时，能量过大，飞过着陆场，将初始迎角指令减少1°，进行时间迭代。再次判断两者的关系，若实际高度已经小于标称高度，或者实际高度比标称高度仅高不到500 m，则该迎角指令可以满足返场条件，飞行器可以返回着陆场；若实际高度还远大于标称高度，重复上步骤进行迎角迭代，直到迎角指令<16°时跳出迎角迭代(迎角指令下边界取16°，上边界取29°)。同样，当实际高度小于标称高度时，迎角反向迭代。

当迎角迭代到达边界值时，进入调整待飞距离阶段。当迎角指令迭代到16°时，实际高度依然远大于标称高度，切换进场方式为间接进场；当迎角指令迭代到29°时，实际高度依然小于标称高度，调整HAC位置到最小位置。若实际高度与标称高度之差依然>500 m，则飞行器无法返回着陆场，算法结束。轨迹迭代算法流程图如图5所示。

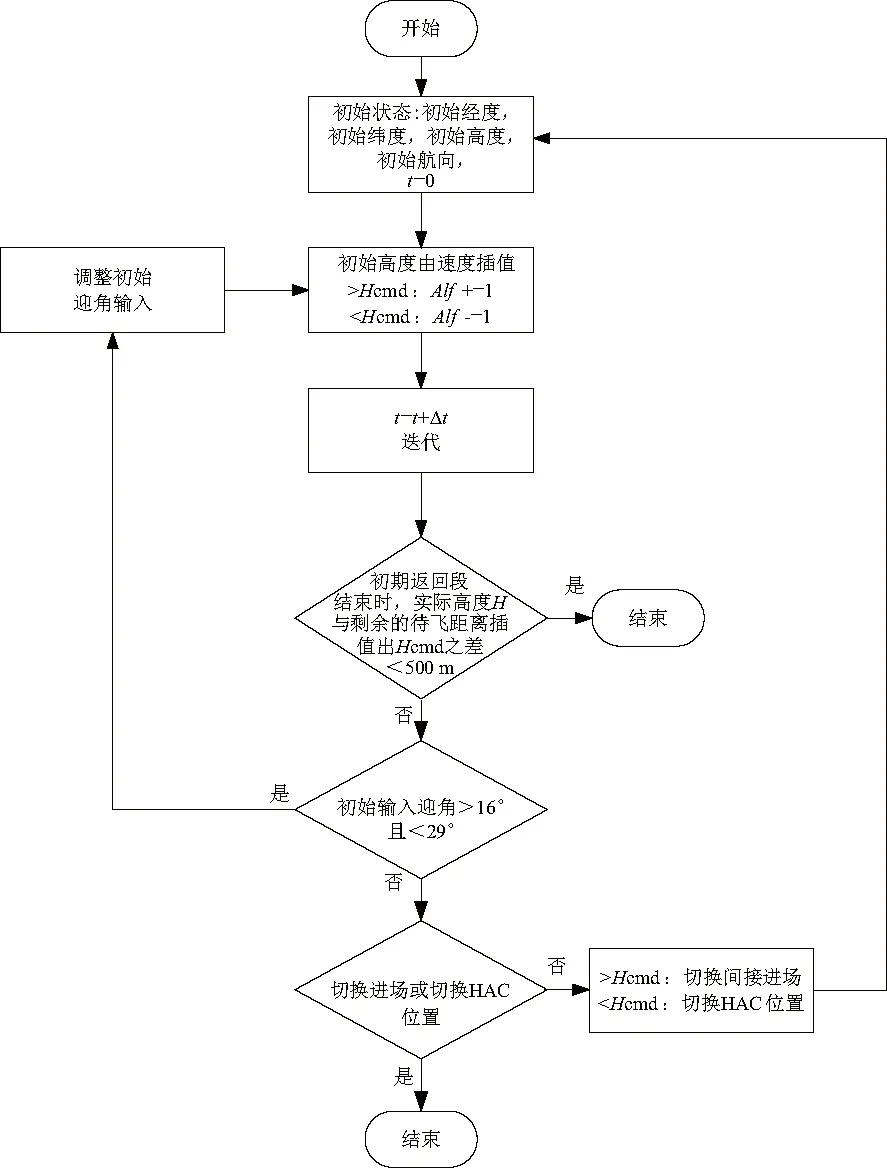
图5 轨迹迭代算法流程图

6 仿真实例验证

给定3个初始返回状态A、B、C，如表2所示，通过上述轨迹迭代算法判断这3个不同的状态能否返回着陆场。

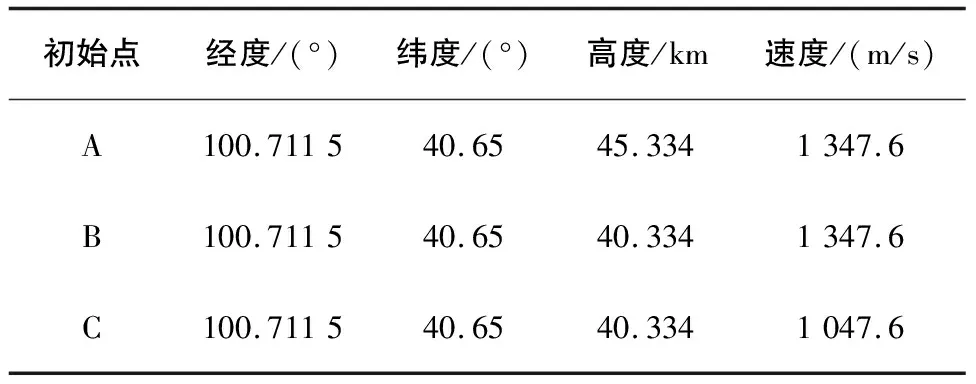
表2 初始返回点状态

图6是A点的返场状况、图7是B点的返场状况、图8是C点的返场状况。蓝色线是调整迎角指令时的状态变化，绿色线是初期迎角指令一定，调整HAC位置的状态变化，红色线是最后一次轨迹迭代的结果。从图6中可以看出，调整迎角和HAC位置可以显著改变返场能力，但因为初始返回点高度、速度过大，初期返回段结束时，高度远远大于指令高度，因而在迎角指令和HAC位置的可调范围内，飞行器不能返回着陆场；相比较状态A、状态B初始高度降低，初期返回段结束时高度更低，由最后一条红线所示，经过迭代，飞行器正好可以返回着陆场(本刊为黑白印刷，如有疑问请咨询作者)。

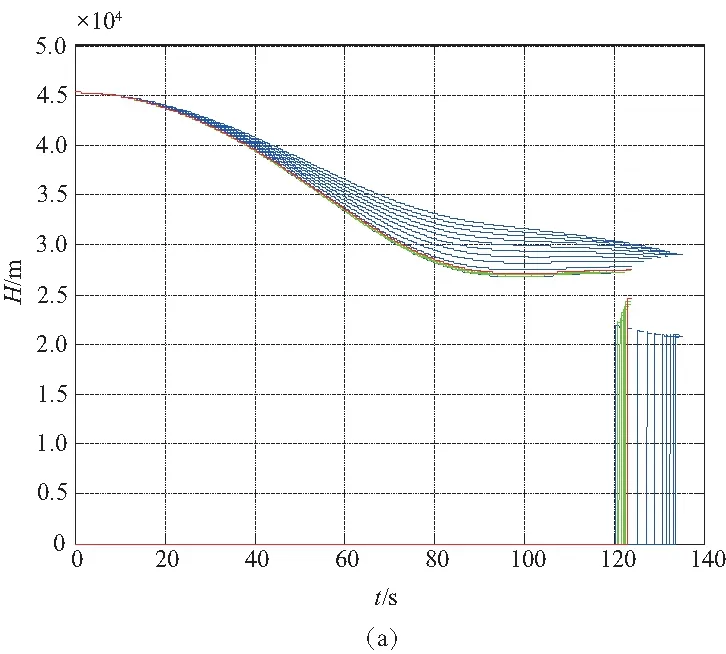
图6 A点返场曲线

图7 B点返场曲线

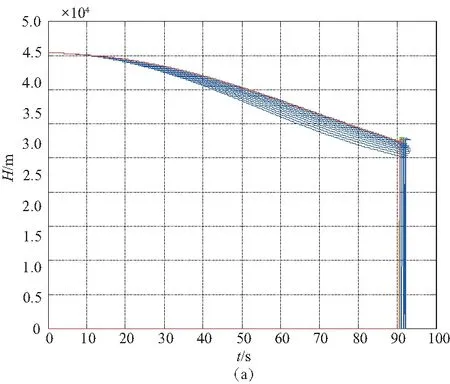
图8 C点返场曲线

相比较状态A和状态B，状态C的初始高度和速度均低，初期返回段结束时的高度明显低于指令高度。由上文知，增大初期返回段的迎角指令，调近HAC的位置更低，经过迭代，发现飞行器依旧不能返回着陆场。

7 结语

本文设计一种制导参数迭代算法，用来判断亚轨道飞行器能否返回着陆场。由于初期返回段高度较高，空气稀薄，气压低，制导系统纵向无法规划高度和动压剖面，无法根据初期返回点的能量状态判断飞行器的航程能力，进而判断能否返场。通过调整初期返回段的迎角指令，调整HAC位置和切换进场方式改变待飞距离，在制导算法的迭代次数内找到一组参数满足高度的判断条件，则当前状态的飞行器能返回着陆场，否则算法结束迭代，不能返场。最后通过具体的实例验证制导参数迭代算法的准确性。