平纵组合路段事故严重程度致因辨识模型

戢晓峰，吴亚欣，郝京京，房 锐，胡澄宇

(1.昆明理工大学交通工程学院，昆明650504；2.西南交通大学交通运输与物流学院，成都610031；3.云南省交通规划设计研究院陆地交通气象灾害防治技术国家工程实验室，昆明650200)

0 引 言

平纵组合路段(Combined Horizontal and Vertical Alignments，CHVA)具有平曲线与纵坡组合的特点，是公路运输安全的瓶颈路段[1].尤其是山区公路，由于地形陡峭常出现弯道与长大下坡或曲线组合的情况[2]，因线形参数对行车安全有显著影响，其安全形势更为严峻.相关统计表明，约15%的交通事故发生在CHVA.因此，对平纵组合路段事故严重程度(Severity of Traffic Accident on Combined Horizontal and Vertical Alignments，STACHVA)致因进行辨识，可有效保障公路行车安全.

近年来，国内外学者深入探索道路事故严重程度与人、车、路及环境之间的关系，但主要集中于高速公路，鲜有对STACHVA 的影响研究.Benlagha等[4]研究车辆、驾驶员等因素对事故严重性的差异性影响机制，冯忠祥等[5]发现时间和天气是影响绕城高速事故严重程度的关键致因.上述研究均可为CHVA 的事故致因分析提供理论依据，但对于CHVA来说，数据获取难度及其致因与高速公路存在显著差异，故影响高速公路事故严重程度的关键因素并不能直接应用于CHVA.此外，关于事故严重程度的致因研究多基于有序概率模型，该类模型的自变量选择具有局限性，往往忽略了不满足某些假设但对因变量有显著效应的自变量.Kalyani等[6]通过构建有序Probit模型表明受害人性别、车辆类型等因素对3种严重程度等级事故的不同影响，王鹏等[7]应用有序Probit 模型识别出道路线形、交通量等5个因素可显著影响追尾事故严重程度.上述有序模型均进行了比例优势假设(Proportional Odds Hypothesis，POH)，即相同自变量对因变量的影响不会随着等级的不同而变化，但从交通事故的随机性来看，部分自变量因违反该假设而被忽略，进而影响模型整体拟合度和科学性.

综上，针对传统模型无法精准识别及量化STACHVA 致因的不足，本文建立有序Logit 模型(OLM)选取影响事故严重程度的显著自变量，通过构建偏比例优势模型(PPOM)进行优化，形成STACHVA 致因辨识的TSM 模型，进一步获取各关键自变量对不同等级事故严重程度的边际效应.最后，选取元双公路元谋—牟定段进行案例分析，旨在为交通安全部门制定针对性的管控政策提供理论依据.

1 变量选取

1.1 因变量选取

根据公安部发布的《交通事故统计暂行规定》，我国按每起事故的伤亡人数及财产损失，将事故严重程度划分为死亡、重伤、轻伤和财产损失事故4类.因此，本文结合实地监测的事故数据，将事故严重程度划分为轻微、一般及严重3类，如表1所示.

表1 STACHVA划分标准Table 1 Classification of STACHVA

1.2 自变量选取及测量

结合道路交通安全影响机制，本文从人[4]、车[6]、路[5]、环境[8]这4 个子系统中选取事故严重程度的影响变量，如图1所示.首先，对选定的32 个变量进行预处理，连续变量采用实际变量值进行赋值；对于分类变量，二分类变量赋值为0 和1，多分类变量需引入哑变量，生成预处理后的自变量38 个.其次，利用SPSS 对38 个自变量进行多重共线性检验，并采取逐步剔除、多次迭代的方式依次删除小车平均小时交通量、空间占有率、总流量及V/C 等4 个VIF 大于10 的自变量，最终形成34 个自变量.

2 模型构建

由于有序模型在自变量选择上的局限性及参数估计上的粗放性，本文建立事故严重程度致因辨识的TSM模型，如图2所示.第1阶段构建OLM获取显著影响STACHVA的自变量，为第2阶段提供变量基础，采用Brant 对关键变量进行POH 检验；第2 阶段构建PPOM，可运用自动拟合选项对未通过POH 检验的自变量放宽比例优势，使模型拟合度更优.最终，通过TSM 精准识别影响STACHVA的显著自变量，进一步获取各自变量对因变量的边际效应[9].

图1 STACHVA 致因Fig.1 Cause of STACHVA

图2 STACHVA 致因辨识的TSM 模型Fig.2 TSM model for cause identification of STACHVA

2.1 模型定义

OLM是一种用于因变量有次序且多分类的回归模型.交通事故第j等级严重程度的OLM为

本文3类事故严重程度对应的OLM分别为

式中：Yi为第i起事故的严重程度；Xi为自变量向量；βi为相应的参数估计向量；αj为第j等级事故严重程度的截距；J为事故严重程度等级数；K为自变量总数；xk为第k个自变量，k=1,2,…,K；βk为xk的估计参数.

OLM 的前提条件是满足POH，该假设因过于严格常常很难满足，出现部分自变量违反POH 的情况.因此，在OLM 的基础上运用PPOM 进行优化，即

不同等级事故严重程度PPOM分别为

式中：Xi′，Ti′分别为满足、违反POH 的自变量向量；βj，γj分别为第j等级中Xi′、Ti′对应的参数估计向量.

OLM 中参数值估计采用最大似然法，似然函数ln(L)计算公式为

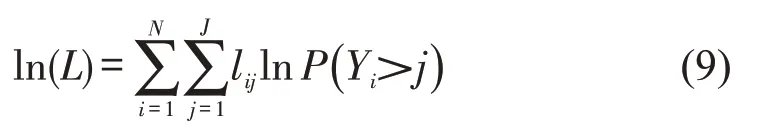
式中：N为事故数量；lij表示第i起事故严重程度为j时，lij为1，否则为0.PPOM 中运用伽马参数化对违反POH的自变量参数值重新估计.

为进一步反映Xi对Yi的影响方向和程度，计算二分类及连续变量的边际效应，即

式中：为影响第j等级事故的第k个自变量；a，b表示为二分类变量对应的不同取值；为的边际效应值，表示从a到b或每单位变化时，对第j等级事故的影响.

2.2 模型检验

本文用似然比指数表征似然比检验结果，即比较最终模型对数似然函数值Lβ与基准模型对数似然函数值L0的相对大小，越接近0，表示模型拟合程度越高，各参数显著性采用t检验方法.采用赤池信息量准则(AIC)和贝叶斯信息准则(BIC)检验模型简约性与拟合数据优良性.

3 实例分析

3.1 研究路段及数据来源

(1)研究路段概况.

相较于单一平曲线与竖曲线，CHVA的车辆运行风险更高[3].为保证行车安全，应合理规定CHVA线形参数，但现有公路设计规范对CHVA 线形参数的规定缺乏定量标准，易出现单一线形要素满足规定而CHVA 事故居高不下的情况.本文以元双公路元谋—牟定段为例，其全长约77.8 km，设计速度60 km/h，为典型的山区二级公路，具体几何特征如表2所示.

表2 研究路段的几何特征Table 2 Geometric characteristics of investigative sections

由表2可知，部分CHVA平曲线半径及纵坡坡长的最小值未满足单一线形规范要求；经统计可知，不满足纵坡坡长及平曲线最小半径要求的分别占14.38%、6.07%；通过调研可知，本文涉及的CHVA 约占元谋—牟定段全长的42.3%.因此，该路段行车环境相对复杂，对行车安全极为不利，是公路运输的高风险路段.

(2)数据来源.

本文获取元谋—牟定段平纵组合路段2013—2017年的交通事故、道路属性、历史天气及交通流数据，如表3所示.经数据集匹配，初始数据共315条，剔除信息不全的数据，最终形成匹配数据集313条，数据有效率达99.4%.

3.2 模型估计结果

运用STATA15.0 进行求解，同时采用反向逐步选择法，经过13次迭代最终筛选出OLM中置信度大于95%的10 个自变量，分别为驾驶人性别(Fdg)、涉及车辆数(Fnv)、平曲线曲率(Fchc)、竖曲线曲率(Fcvc)、竖曲线长度(Flvc)、纵坡坡度(Fdls)、接入口(Fas)、阴天(Fc)、大车比例(Frlv)及小车与无防护型车的平均车速差(Fsuv).经Brant检验发现Fnv、Fchc、Fcvc、Flvc及Fdls这5 个变量的p值均小于0.05，表明在95%置信水平下，这5 个自变量统计性并不显著，违反了POH，故通过构建PPOM进行参数优化，结果如表4所示.

表3 数据来源Table 3 Sources of data

表4 TSM 模型估计结果Table 4 Estimation results of TSM model

由表4可知，TSM 较OLM 而言，AIC、BIC、分别下降了14.924%、12.742%、17.500%，故模型更简约且拟合程度更优.对TSM 参数估计结果进一步分析，可得10 个显著自变量对事故严重程度的影响机制如图3所示.

由图3可知：

(1)除驾驶人性别、小车与无防护型车的平均车速差、接入口等对STACHVA 有显著负效应，其余变量对STACHVA均呈现正效应.

(2)如图3(a)所示，从轻微事故对一般和严重事故的PPOM来看，大车比例、平曲线及竖曲线曲率对STACHVA的影响较大；如图3(b)所示，从轻微和一般事故对严重事故的PPOM来看，大车比例、纵坡坡度及平曲线曲率对STACHVA的影响较大.

图3 STACHVA 影响机制Fig.3 Influence mechanism of STACHVA

(3)总之，大车比例对STACHVA的影响最大，主要是大车在特定速度下具有更大的动量，使发生严重事故概率更高；而线形因素对STACHVA的影响较大，说明CHVA 因降低了驾驶员的可见度和机动性，使行车风险性增加.

3.3 边际效应分析

根据3.2节的分析，计算显著自变量对因变量的边际效应，说明各自变量对STACHVA的影响方向和程度，如表5所示.

表5 显著自变量对因变量的边际效应Table 5 Marginal effect of significant independent variables on dependent variable

由表5可以看出：

(1)从驾驶人层面来看，与女性相比，男性驾驶员发生一般和严重事故的概率分别减少10.181%和0.400%，说明男性较女性驾驶情绪稳定及身体承受创伤力强.

(2)从车辆层面来看，与单车事故相比，多车事故由于涉及车型各异、事故形态复杂，发生一般和严重事故的概率分别增加5.183%和0.465%.

(3)从道路属性层面来看，接入口使一般和严重事故的发生概率分别减少10.855%和3.611%，说明驾驶员对接入口的危险感知较敏感，行车较谨慎，故事故严重程度减轻；平曲线曲率、竖曲线曲率、竖曲线长度及纵坡坡度等4个变量每增大一个单位，发生一般和严重事故的概率均会不同程度地增加，说明线形条件较差显著加重事故后果，从而验证了线形对STACHVA影响重大，改善道路线形是减轻事故严重程度的关键举措.

(4)从环境层面来看，阴天较晴、雨天发生一般和严重事故的概率分别增加2.899%和1.212%，这主要是因为晴天对较高严重程度的事故影响较小，而雨天等恶劣天气下驾驶员警惕性高，一定程度上可减轻事故严重程度；大车比例每增加一个单位，车辆间车头时距减小，发生一般和严重事故的概率分别增加3.788%和1.374%；小车与无防护型车的平均车速差每增加一个单位，发生一般和严重事故的概率分别减少0.604%和0.021%，主要是由于车速差异性较大，车辆间相互影响小，可减少恶性交通事故的发生.

4 结 论

CHVA交通安全一直是痛点问题，本文通过构建STACHVA致因辨识的TSM模型，对STACHVA致因的影响方向和程度进行精准识别和定量解析.研究发现：所构建的TSM 模型相比传统的有序概率模型拟合度更优；驾驶人性别、小车与无防护型车的平均车速差、接入口对一般及以上事故严重程度具有负效应，涉及车辆数、平曲线曲率、竖曲线曲率、竖曲线长度、纵坡坡度、天气、大车比例对一般及以上事故严重程度具有正效应；就影响程度来看，从高到低依次是接入口、驾驶人性别、竖曲线曲率、平曲线曲率、涉及车辆数、大车比例、纵坡坡度、天气、小车与无防护型车的平均车速差、竖曲线长度.本研究可为交通安全部门开展CHVA风险监管工作提供决策参考.本文仅分析了单一变量对STACHVA的影响，未来将进一步探究多变量间的耦合作用对STACHVA的影响机理.