冰雪条件下中国驾驶员跟驰行为及模型研究

杨龙海，张 春，仇晓赟，吴应涛，李 帅，王 晖

(1.哈尔滨工业大学交通科学与工程学院，哈尔滨150090；2.深圳市城市交通规划设计研究中心股份有限公司,广东深圳518000；3.深圳高速工程顾问有限公司，广东深圳518000；4.中国路桥工程有限责任公司，北京100011)

0 引 言

冰雪条件下，由于不同驾驶员感知和反应状况不同[1]，在跟驰行驶过程中对速度、间距等因素的控制较正常天气条件产生各异性变化，对交通流运行造成不同程度干扰.学者研究了冰雪条件对平均行车速度[2]、通行能力[3]、平均车头时距[4]等宏观交通流参数的影响，受实验数据获取困难等因素影响，对冰雪条件下微观层面驾驶员行为特性的研究较少.Hjelkrem等[5]定义了跟驰情况下驾驶员选择风险等级指标(Chosen Risk Index，CRI)，以正常条件为参考，发现冰雪条件下驾驶员会调整自己的行为，CRI 降低，寓意着驾驶员在冰雪条件下会降低所选择的风险指数.跟驰行为建模方面：多数跟驰模型没有对驾驶人如何思考及采取措施的过程进行合理阐述[6]，尤其是在冰雪条件这一复杂驾驶环境下.Yang等[7]考虑冰雪条件下实时最大减速度的影响改进了智能驾驶员(Intelligent Driver Model，IDM)模型，并将改进模型应用于自适应巡航系统，在两种场景下进行仿真，改进模型显示出比IDM 模型更好的效果，但该模型未考虑驾驶员的行为特性.为更真实地描述不同驾驶员在冰雪条件下的跟驰行为，需考虑冰雪条件这一环境因素，引入对比研究，结合不同驾驶员行为特性，构建新的车辆跟驰模型.

本文组织驾驶员进行正常条件和冰雪条件下的车辆跟驰试验，采集驾驶员驾驶行为数据，采用任务难度均衡理论构建人类因素模块，将其引入改进的IDM 模型中，从而构建冰雪条件下考虑驾驶员行为特性的跟驰模型.使用实车跟驰试验采集到的轨迹数据对模型进行标定和验证.结果显示，引入人类因素参数可以较好地体现冰雪条件下驾驶员行为特性的变化，新模型在6个仿真场景中的表现都优于传统IDM 模型，且表现出更好的鲁棒性.

1 冰雪条件下考虑驾驶员行为特性的跟驰模型构建

1.1 数据来源

在哈尔滨市长江路禧龙大街至绕城高速间的路段上开展实车跟驰试验，试验设备采用厘米级P3-DT 北斗高精度定位测向接收机，采样频率5 Hz.试验包括不同速度下的稳定跟驰试验及不同幅度的加减速试验.招募哈尔滨市本地驾驶员11人，分别在正常条件和冰雪条件下开展试验.11名驾驶员均为男性，年龄在24～32 岁(均值Mean 为27.4 岁，标准差STD 为2.69)，均持有C1 及以上驾驶证，驾龄均大于3年.

每种条件下，试验分2组进行，第1组6人(1～6号)，第2 组6 人(1 号，7～11 号)，1 号为头车，预先对1号车设置速度值以进行车队速度控制.稳定跟驰状态下，头车开启定速巡航系统，此时头车速度标准差小于0.09 km⋅h-1，以既定速度匀速行驶，后随车辆以近似速度跟随行驶.稳定跟驰数据是从后随车辆速度与头车速度近似时提取出来的.正常条件下，试验共采集有效数据点284 218 条，每名驾驶员平均驾驶时间1.4 h，平均行驶里程30 km.

北方寒冷地区降雪后冰雪路面形态通常经历如下过程：开始降雪之后，路面积雪受车辆碾压首先形成一层粗糙的冰膜；随着降雪继续和车辆碾压，路面形态变为轻度压实雪；而后由于城市大规模清雪措施的开展，覆雪冰膜路面成为冰雪条件下最常见的路面形态，存在时间也相对较长，对城市交通的影响较大.因此，本文选取覆雪冰膜路面形态作为研究重点，在这该种冰雪路面形态下进行车辆跟驰试验.6号驾驶员因个人原因未参与试验，其余均与正常条件一致.冰雪条件下，试验共采集有效数据点313 890条，每名驾驶员平均驾驶时间1.7 h，平均行驶里程35 km.

1.2 数据分析

对比分析驾驶员在稳定跟驰状态下的车头时距，车头时距标准差及两个参数在冰雪条件下的变化幅度，结果如表1所示.

表1 车头时距变化对比Table 1 Comparison of time headway changes

稳定跟驰状态下：除4 号、9 号外，其余7 名驾驶员在冰雪条件下均选择更大的车头时距；除7号驾驶员外，其余8 名驾驶员的车头时距波动幅度(标准差)出现不同程度的降低.这说明绝大部分驾驶员在稳定跟驰过程中采取了明显的风险补偿行为，且操作更加谨慎.

分析前、后车速度差与后车加速度的分布区间及频率，如图1和图2所示.发现，速度差与加速度的分布区间均收窄，中心区域出现频率上升，这说明冰雪条件下驾驶员更倾向于采取与前车一致的速度行驶，从而避免频繁的加减速操作.图3和图4是对加速度分布区间的统计，表明正常条件下驾驶员的加减速度区间宽而分散，而在冰雪条件下驾驶员的加减速度的分布区间窄而集中(均值μ相同，均方差σ由0.447 降低至0.347)，说明冰雪条件下驾驶员采取的加减速度值更小，这也符合冰雪条件下驾驶员的谨慎心理及其外在表现.

1.3 理论背景

Fuller[8]从人类因素的角度提出任务能力交互(Task Capability Interface,TCI)模型，其中，驾驶任务的难度主导着驾驶员行为.该模型中，任务难度(Task-Difficulty,TD)产生于驾驶能力与任务需求之间的动态交互作用.驾驶员的驾驶能力受驾驶员结构特征(如通过教育和培训而形成的知识和技能)和生物学特征(如感知敏锐度、反应时间和视觉敏锐度)限制.

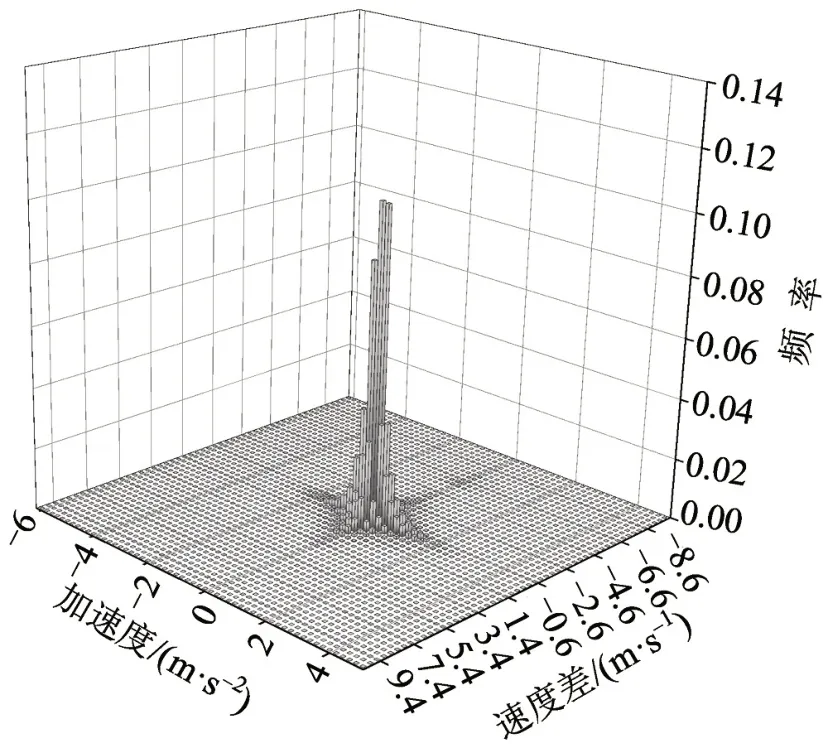
图1 正常条件速度差与加速度分布Fig.1 Velocity difference and acceleration distribution under normal conditions

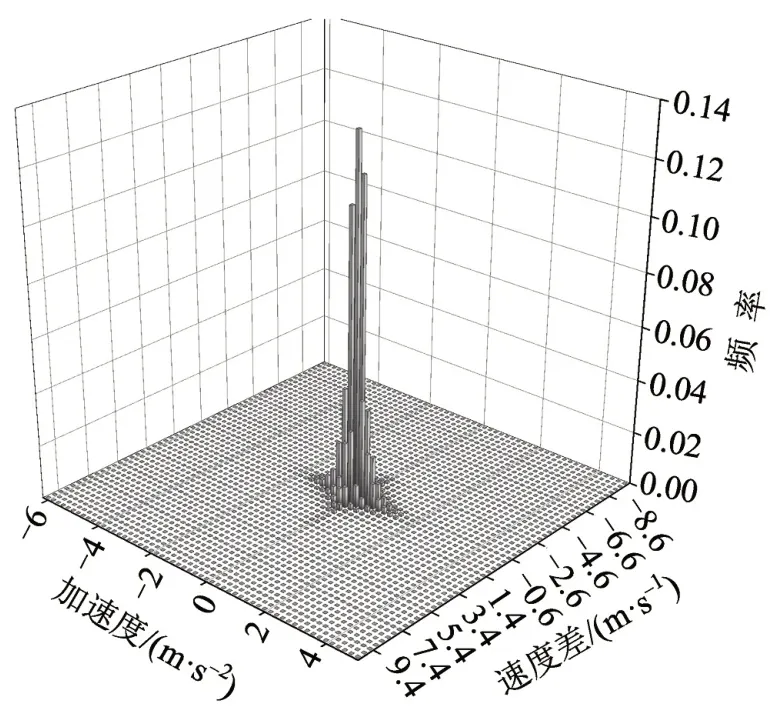
图2 冰雪条件速度差与加速度分布Fig.2 Velocity difference and acceleration distribution under snow and ice conditions

任务需求则受环境条件(如路面条件、能见度)，车辆特性(如发动机功率、制动和驾驶员辅助系统)，车辆相对于其他道路使用者的速度和位置等因素综合作用.TCI模型通过驾驶能力与任务需求之间的交互作用体现车辆的受控或碰撞的状态.当驾驶能力超过任务需求时，驾驶任务难度低，车辆运行处于驾驶员的控制之下；当因多种可能原因导致任务需求超过驾驶能力时，驾驶任务难度升高，车辆会有失控风险.TCI模型机理如图5所示.

图3 正常条件加速度频率分布直方图Fig.3 Frequency distribution histogram distribution under normal conditions

图4 冰雪条件加速度频率分布直方图Fig.4 Frequency distribution histogram distribution under snow and ice conditions

图5 TCI 模型机理图Fig.5 Task-capacity interface mode

TCI模型的关键假设是任务难度均衡理论.根据该理论，驾驶员通过调节车速、车头时距等控制变量，持续实时地做出决策，将感知到的驾驶难度维持在其可接受的范围内.如果感知到的任务难度高于可接受的极限，例如在冰雪路面条件下，由于路面冰滑，驾驶员大多会降低速度，增大间距，以降低任务难度水平至可接受极限内.驾驶员所针对的任务难度范围是由他们感知到的从事某一特定难度水平任务的能力和动机决定的.

1.4 跟驰模型构建

1.4.1 任务难度模块构建

本文参考Saifuzzaman[9]的假设，将任务需求与驾驶能力之间动态交互视为任务需求和驾驶能力的比值.Fuller指出，在任何情况下，任务需求都可以用车辆的速度和与前车的间距来解释.在其他条件相同的情况下，速度越快或间距越小，用于决策和响应的时间就越短，从而导致任务需求增加.

驾驶员的驾驶能力因存在很多难以观测变量(如生物学特征)，难以测量.有研究发现，驾驶经验与车头时距选择之间存在负相关，经验丰富的驾驶员比新手更有可能保持较短的车头时距[10].跟驰行驶过程中，车头时距骤减会使认知和心理方面的风险感知上升，感知到的风险越大越耗费精神来应对，在这种情况下驾驶员会认为驾驶任务困难、危险、不舒适.因此，本文假设驾驶员能力与驾驶员期望车头时距选择负相关，即驾驶能力越强，期望车头时距越小.

冰雪条件下驾驶员对自身驾驶行为进行修正，引入认知风险参数(δn)捕捉冰雪条件对不同驾驶员驾驶行为的影响.δn＞0 表示驾驶员受冰雪环境影响，感知到驾驶能力降低的风险；δn=0 表示驾驶员未受当前冰雪环境的影响；δn＜0 表示驾驶员不仅未采取风险补偿措施，反而表现出更激进的行为.综上，构建任务难度模块为

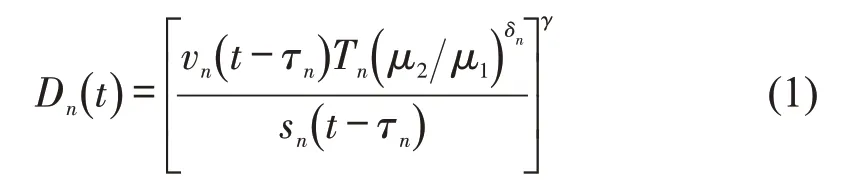
式中：Dn(t)为第n号驾驶员在t时刻感知到的任务难度；vn为第n号车辆的瞬时速度；Tn为第n号驾驶员期望车头时距；μ1为冰雪条件下的路面附着系数(覆雪冰膜路面取值为0.3)；μ2为标准路面条件下的路面附着系数(正常沥青路面取值0.6)；δn为冰雪条件下第n号驾驶员的认知风险感知系数；sn为第n号车辆与前车间距；τn为修正后第n号驾驶员的反应时间，τn=τ+φ，其中，τ为正常反应时间，φ为受外界驾驶环境变化影响产生的反应时间变化量；γ为驾驶员对任务难度水平的敏感系数.

将任务难度模块引入跟驰模型中，根据任务需求和驾驶能力之间的关系，对原跟驰模型中输出的速度/加速度进行动态修正.

1.4.2 智能驾驶员模型改进

选择智能驾驶员模型(IDM)[11]作为基础模型，其形式为

式中：an(t)为t时刻第n号车辆采用的加速度；a1为最大加速度；vn(t)为t时刻第n号车辆的速度；sn(t)为t时刻第n号车辆与前车的间距；vn-1(t)为t时刻前车速度；Vn为第n号驾驶员期望速度；st(t)为t时刻期望间距；s1为拥挤交通中车辆所需的最小间距；b为舒适减速度；Δvn(t)为第n号车辆与前车速度差.

原始IDM模型中，Δvn(t) 为较大负值时，期望间距产生负值，本文修正期望间距公式为

当实际间距大于跟驰阈值s2时，驾驶员以期望的最大速度vmax行驶，即vn(t)=vmax，车辆处于均衡状态.因此，当实际间距远大于期望间距时，修改模型为

将车辆跟驰中的交通状态划分为4个状态，令参数a1=0.8 m⋅s-2，T=1.5 s，b=1.5 m⋅s-2，利用式(5)计算期望间距，进一步推算期望间距与实际间距的差值，绘制间距差与速度差关系，研究驾驶员在不同驾驶任务需求时的驾驶行为.以5号驾驶员数据为例，其在低速、中速、高速3种跟驰状态下的间距差与速度差关系如图6所示.

由图6可知，驾驶员在跟驰行驶过程中受间距及速度差的外界刺激及自身驾驶能力的影响实时对车辆行驶状态进行动态调整，从而保持间距在期望间距，速度与前车一致的状态，间距差—速度差围绕中心点震荡，进一步证明了任务难度均衡理论的正确性.图7总结了驾驶员在不同交通状态下的驾驶行为表现.

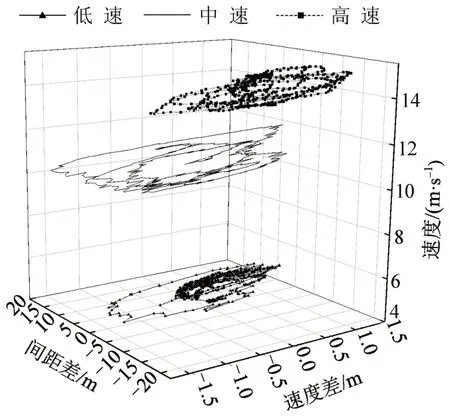
图6 间距差与速度差关系Fig.6 Relation between distance difference and velocity difference

图7 不同交通状态下的驾驶员操作Fig.7 Driver operation in different traffic conditions

结合驾驶员在不同交通状态下的操作表现，对IDM模型添加约束条件，得到改进IDM模型为

1.4.3 考虑驾驶员行为特性的跟驰模型构建

从图6可以看出，在不同行驶速度下，驾驶员的期望间距不同；另外，由于期望间距式(8)得出的期望间距存在偏差，导致本应原点对称的图形出现上下位移.因此，在改进IDM 模型中引入TD 修正期望间距，得到TDIDM模型为

限于冰雪条件下高速巡航的危险性，本文未开展高速巡航状态下的行驶实验，但对跟驰状态下，即sn(t)＜s2的情况进行模型标定和验证.

2 跟驰模型标定

2.1 数据预处理

通过等帧间隔采样可以在一定程度上避免得到过多的冗余轨迹点，但帧间的不稳定特性仍会使获得的采样点中存在不能正确反映车辆运行趋势的噪声轨迹点.为此，采用巴特沃斯滤波器对轨迹序列进行平滑去噪处理，继而推算得到间距、速度、加速度等数据，部分参数滤波后效果如图8所示.

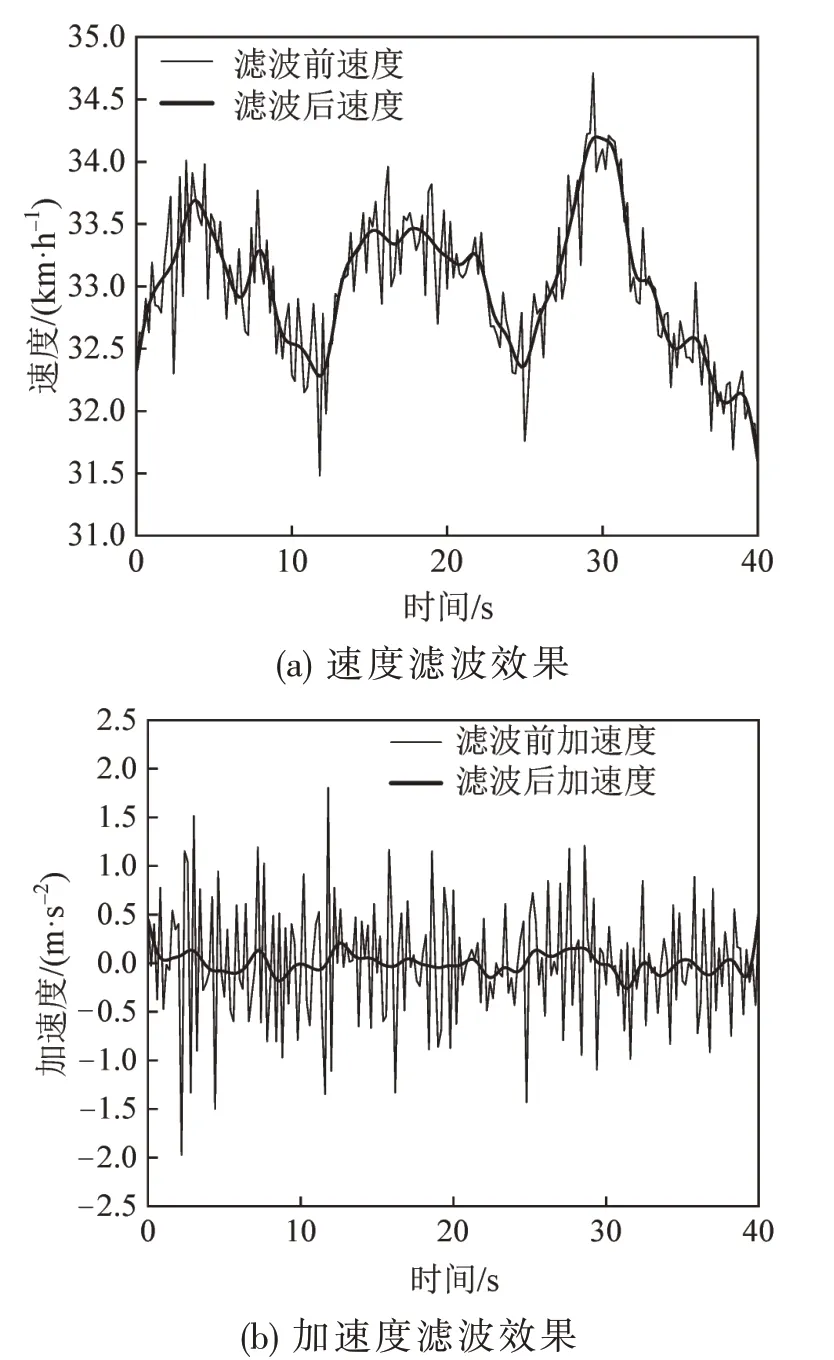
图8 滤波效果图Fig.8 Filtering effect diagram

2.2 目标函数选择

以均方根归一化误差ERMSNE作为目标函数.

式中：为间距仿真值；为间距实际观测值；N为车辆编号

模型标定使用MATLAB 中遗传算法工具箱，设定种群规模为200，最大迭代数为600，停滞代数为100.此外，为提高计算效率，设置标定参数的上下界，如表2所示.

表2 模型标定参数设置Table 2 Parameter settings for model calibration

由于遗传算法是随机的，每次优化计算得到的解略有不同，为找到更接近全局最优的解，每位驾驶员的数据重复优化计算20 次，选择误差(即ERMSNE)最小的一组参数.

2.3 标定结果

分别使用正常条件和冰雪条件下的轨迹数据标定原始IDM 模型.TDIDM 的两个人类因素参数(反应时间变化量、认知风险参数)使用冰雪条件下的轨迹数据进行标定，其余非人类因素参数均使用正常天气条件下的轨迹数据进行标定.标定结果如表3～表5所示.

表3 原始IDM 模型标定结果Table 3 Calibration result of IDM

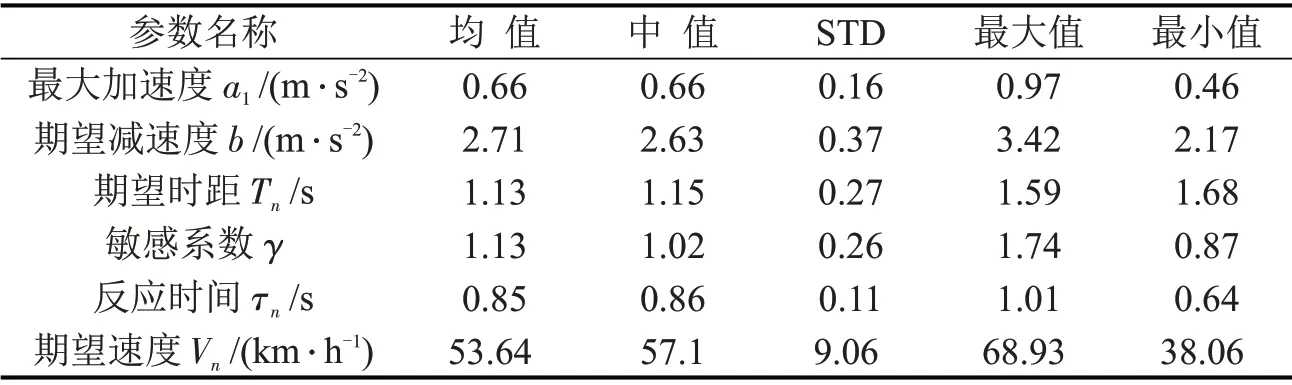
表4 TDIDM 标定结果(正常条件)Table 4 Calibration result of TDIDM(normal conditions)

表5 TDIDM 标定结果(冰雪条件)Table 5 Calibration result of TDIDM(snow and ice conditions)

9 名驾驶员的两个人类因素参数标定结果如表6所示.除3、4、10 号驾驶员外，另外6 名驾驶员的反应时间在冰雪条件下均出现不同程度的增加，但这与驾驶次任务导致的反应时间延长不同，冰雪条件下驾驶员操作更加谨慎，倾向于在准确判断前车驾驶意图之后再采取加减速操作.4号和9号驾驶员的认知风险系数为负数，未感知到冰雪条件的风险，其余7 名驾驶员认知风险系数为正数，说明这7 名驾驶员采取了风险补偿措施(车头时距增加)，这一结论与实际数据统计结果(表1)完全一致.

为更清晰地解释认知风险系数的作用，选择认知风险系数最低(-0.12)的9号及最高(1.76)的10号以9 m⋅s-1稳定跟驰时的轨迹数据进行对比分析，结果如图9所示.

从图9可以看出，冰雪条件下，9 号和10 号驾驶员在面对相同驾驶环境(跟驰行驶速度相同、天气条件相同)时，由于风险认知不同，驾驶行为变化存在显著差异.10 号驾驶员采取明显的风险补偿措施，跟驰间距出现明显上升(均值由17.89 m上升到28.5 m)；9号驾驶员并未采取相应的风险补偿措施，其驾驶行为没有出现明显变化.

表6 9 名驾驶员反应时间变化量及认知风险系数标定结果Table 6 Calibration results of reaction time variation and cognitive risk coefficient of 9 drivers

3 有效性验证

利用驾驶员剩余轨迹数据进行仿真，以验证模型的有效性.考虑6个验证场景，如表7所示.这6 个验证场景可对正常条件和冰雪条件驾驶场景下的模型有效性进行仿真验证，并可以检验模型对不同标定参数的鲁棒性.

图9 9 号和10 号驾驶员行为特性对比Fig.9 Comparison diagram of NO.9 and NO.10 drivers'behavior characteristics

验证场景1 和验证场景2 可评估模型在正常条件下的表现，其他验证场景均为评估模型在冰雪条件下的表现.有效性验证结果如表8所示.9名驾驶员，6个仿真场景共计54个仿真实例中，有53例TDIDM模型误差水平优于IDM模型.

表7 仿真场景设置情况Table 7 Simulation scenario settings

此外，总结每种验证场景中9名驾驶员的平均验证误差，如表9所示.可以看出，在每个验证场景中，TDIDM的表现均优于原始IDM.

根据表9可得：TDIDM 模型使用同一标定参数集即可描述正常条件和冰雪条件下的驾驶员行为，引入两个人类因素参数可以很好地捕捉驾驶员在冰雪条件下驾驶行为变化；在验证场景3 和4中，对比有无人类因素参数，即认知风险系数和反应时间变化量参数的TDIDM模型，有人类因素参数的TDIDM 产生了较小的误差；参数值变化对TDIDM 模型影响较IDM 模型更小，这说明由于TD的引入，TDIDM模型的鲁棒性更好.

表10统计分析表明，原始模型和改进模型的ERMSNE具有显著性差异.

表8 验证场景ERMSNE 对比Table 8 Validation ERMSNE comparison (%)

统计检验进一步证实，有人类因素参数TDIDM模型的ERMSNE显著低于无人类因素参数模型(t=12.75,p＜0.001).因此可知，引入两个人类因素参数能够捕获冰雪条件下驾驶员的风险补偿行为.

最后，以2 号驾驶员为例，绘制正常条件和冰雪条件下速度和间距的实际观测值与仿真值的对比图，如图10所示.

表10 每种验证场景两个模型的ERMSNE 差异水平Table 10 ERMSNE differences between two models for each validation scenario

图10 2 号驾驶员速度、间距观测值与仿真值对比图Fig.10 Comparison between observed and simulated values of NO.2 driver's speed and distance

由图10可以看出，TDIDM模型的表现始终优于IDM 模型.虽然在验证场景1 中IDM 模型仿真效果也比较合理，但当使用相同模型参数描述验证场景3冰雪条件下的驾驶员行为时，IDM模型并没有很好的效果，这是因为它没有捕捉到驾驶员在冰雪条件下的风险补偿行为.相反，TDIDM模型的人类因素参数成功地捕捉到了这种风险补偿行为，使验证误差较小.在验证场景5中，使用正常条件数据标定的TDIDM 模型甚至比用冰雪条件数据标定的IDM模型表现更好.

4 结 论

本文在正常条件和冰雪条件下分别开展实车跟驰试验，通过对实验数据的分析，构建冰雪条件下考虑驾驶员行为特性的跟驰模型，并对模型进行标定及有效性验证，得到结论：

(1)在跟驰行驶过程中，驾驶员会根据外界刺激及自身驾驶能力实时调整车辆行驶状态：驾驶员尽量保持间距在期望间距、速度与前车保持一致的状态，其间距差—速度差图像围绕中心点震荡，从数据上证实任务难度均衡理论的正确性.

(2)冰雪条件下驾驶员采取风险补偿行为，更倾向于采取与前车一致的速度行驶，避免频繁的加减速操作.其车头时距波动幅度、速度差与后车加速度的分布区间均较正常条件收窄.

(3)所构建的TDIDM 模型及标定结果与实际数据统计结果一致，验证了引入人类因素参数可以较好地捕捉冰雪条件下驾驶员行为特性的变化.有效性验证结果显示TDIDM模型在6种仿真场景下的ERMSNE水平都显著低于IDM 模型，且TDIDM模型表现出更好的鲁棒性.