利用强部分平衡t-设计构造分裂认证码
王秀丽,曹 苗,王利娜
1.中国民航大学理学院,天津300300
2.北京师范大学静海附属学校中学部, 天津301600
随着信息技术的快速发展,信息安全问题在人们的生活中变得越来越重要.信息安全的两个主要研究内容是信息的保密和认证.信息保密是通过对所需传送的信息进行加密来保护信息,防止信息被他人窃取.信息认证的目的在于防止非法用户进入认证系统,防止接收不明身份的信息,使接收方在收到信息后能够确认信息的来源是正确的.此后,对两个方面进行认证:对信息的发送者和接收者的身份进行验证;对信息的完整性进行验证,验证信息在信道传输过程中,是否有被篡改或延迟的情况发生.
在研究保密问题中,Shannon[1]于20世纪40年代首次利用信息论的方法并提出了完善保密系统的概念.Simmons[2]在研究信息的认证问题时也应用了信息论的方法.这些工作为信息认证奠定了理论基础.1985年,Simmons[2]首次提出了认证码的概念,现在认证码已成为研究认证理论的重要问题之一.1974年,Gilbert 等[3]第一次进行认证码的构造.
有限几何是研究认证码的有力工具.2014年,邱双月[4]利用有限域上参数δ=0 的奇异酉空间构造了Cartesian 认证码,但这种方法对于参数δ=1 的奇异酉空间计算较为复杂.2015年,邱双月等[5]对此进行了改进,在参数δ=1 的奇异酉空间中构造了Cartesian 认证码.此外,陈尚弟等[6]利用有限域上的酉几何构造了具有可信仲裁的认证码.代数组合方法是研究认证码的重要方法.2010年,李殿龙[7]利用代数学中的立方幂零矩阵的若尔当标准型构造了Cartesian 认证码,该方法在同等条件下能够认证更多的信源,从而节省了通信成本,并且认证码的安全性得到进一步提升.2009年,裴定一[8-9]在消息认证码中详细介绍了完善认证系统和组合设计之间的关系,并给出了最优认证码、完善认证码的定义及实例.2015年,Safavi-Naini 等在文献[10]中讨论了敌方对接收方进行攻击的最优策略,给出了认证码欺骗成功概率的下界,得到了最优认证码的组合特征.
在传统的认证码中,主要考虑模仿攻击和替换攻击成功的概率,但是在实际通信中,收发双方一般是彼此不信任的[11],Simmons[12]提出了认证码的扩展-带仲裁的认证码,而分裂认证码是研究带仲裁的认证码的一种重要手段.Simmons[12]首次提出分裂认证码的定义,后来众多学者尝试利用各种方法构造性能优良的分裂认证码.Kurosawa 和王永传等[13-14]给出了分裂认证码和带仲裁认证码之间的对应关系.
组合设计作为一种重要的组合结构,在构造认证码和分裂认证码[15-16]中也被广泛采用.其中用带约束的部分平衡t-设计(restricted strongly partially balanced design, RSPBD)构造带仲裁的认证码,是由裴定一等[17]首次提出和运用的,而在利用分裂不平衡区组设计(splitting balanced incomplete block design,SBIBD)构造分裂认证码方面,Huder 和Ogata等[15,18]都进行了开创性的研究并得到了重要的成果.2012年,Liang 等[19]利用可裂设计研究了三重完善分裂认证码.近年来,关于分裂认证码的新成果也很丰硕:2015年,Chen[20]利用射影空间中的特殊子空间及线和面的关联关系,构造了分裂认证码;Matsubara 等在文献[21]中主要研究了可裂平衡区组设计(splitting block design, SBD)的可分解性,提供了具有可分辨性的SBD与其他组合设计的一些等价性,还提供了可解的SBD与其他组合设计的一些等价性.2017–2018年,Liang[22]、Li[23]和王利娜[24]继续利用特殊的组合设计分别构造了几类新的最优分裂认证码,但所用到的理论稍显复杂,组合技巧不易掌握.
本文所构造的认证码创新性主要体现在:基于有限域Fq上的二维向量空间,巧妙地借助线性方程组的理论,构造了带约束的强部分平衡设计;相对于文献[22-23],本文所用理论简单易懂,模拟仿真易于实现;本文是文献[24]研究方法的继续,研究结果同时也将文献[8]中关于完善认证码的构造推广至完善c-分裂认证码;通过举例与文献[15]的相关结果对比发现,在编码规则数目相同的前提下,本文的信源数目大于文献[15]的信源数目;本文所构造的认证码的各阶攻击成功概率都达到了最小.
1 预备知识
本节给出认证码的相关概念,组合设计和分裂认证码的相关定义,两者的关系以及所需结论.
1.1 分裂认证码及Cartesian 认证码的定义
定义1[11]对于一个认证码(S,E,M,f),若编码规则e将信源s编码成多个消息m,则称之为分裂认证码.
此时,对任意消息m ∈M,有m=e(s,r),其中r ∈R,R是特殊的有限集合.对于∀s ∈S,∀e ∈E,定义

分裂是指对于某些信源s ∈S和编码规则e ∈E,有|e(s)| >1.为了能够顺利译码,规定若则有
定义2[11]对于每一个信源s ∈S和每一个编码规则e ∈E,如果|e(s)|=c,那么这个分裂认证码就称为c-分裂认证码.
定义3[8]对于任意信源s ∈S,令M(s)={m ∈M|∃e ∈E,e(s)=m},M(s)是能代表s的所有报文的集合.如果对于任意两个不同的信源s1和s2,M(s1)与M(s2)没有公共元,那么这时认证码(S,M,E)就称为Cartesian 认证码.
1.2 带约束的部分平衡t-设计
定义4[20]设v,b,k,c,λ,t为正整数,tk.一个带约束的部分平衡t-设计RPBDt −(v,b,k×c;λ,0)是一个二元组(X,B), 其中X具有v个元素,B是区组集且满足以下条件,
1)每个区组Bi ∈B(1i|B|=b),都可以表示成长度为c的k个互不相交的子区组的并,即Bi=Bi,1∪Bi,2∪···∪Bi,k,其中|Bi,1|=|Bi,2|=···=|Bi,k|=c;
2)X中任意t子集{x1,x2,···,xt},或在λ个区组Bi=Bi,1∪Bi,2∪···∪Bi,k中同时出现,且xm ∈Bi,jm(jm=1,2,···,k),其中j1,j2,j3,···,jt互不相同,或它们不在任一区组中出现.
定义5[20]一个带约束的部分平衡t−(v,b,k×c;λ,0)设计,如果同时也是带约束的部分平衡r −(v,b,k×c;λr,0)设计,1rt −1,则称(X,B)为带约束的强部分平衡t-设计(RSPBD),记为t −(v,b,k×c;λ1,λ2,···,λt,0).
定理1[20]假设存在一个RSPBDt −(v,b,k×c;λ1,λ2,···,λt−1,1,0)设计,其中t2,则对于k个等可能出现的信源,存在一个t-阶完善c-分裂认证码,具有v个信息和b个编码规则的.相反,如果有一个具有k个信源,v个信息和b个编码规则的t-阶完善c-分裂认证码,那么也就存在一个RSPBDt −(v,b,k×c;λ1,λ2,···,λt−1,1,0),其中λr=(PrPr+1···Pt−1)−1,1rt −1.
Pr为r-阶最佳欺骗攻击成功的概率,r-欺骗攻击是指敌方在观察方使用相同的编码规则,取M为认证码的信息的集合,也是区组设计中样本的集合.取信源S=Fq,在观察到发方发送r(r0)个消息后,敌方在信道中放入不同于发方发送的r个虚假消息,试图使收方接收,并认为它们是真实可靠的.
定义6[8]设Mi1,···,it={mt=(m1,m2,···,mt)|mr ∈M(sir),1rt},在一个t-阶完善Cartesian 码中,假设存在信源集S的一个固定子集si1,···,sit,使任一mt ∈Mi1,···,it,其中Mi1,···,it={mt=(m1,m2,···,mt)|mr ∈M(sir),1rt},都有|E(mt)|=1,那么称这个认证码是I 型完善认证码,否则为II 型完善认证码.
定义7[8]设t为正整数,当编码规则的数目|E|达到下界(P0P1···Pt−1)−1,即|E|=(P0P1···Pt−1)−1,这个认证系统称为t-阶完善认证系统.
对于认证码的构造,主要考虑下述问题:1)Pr尽可能小,保证安全性;2)编码规则尽可能少,减少传输过程中的存储量;3)信源数目尽可能多,增大传输的信息量;4)与普通认证码相比,可裂认证码需增加一定的变量,对消息进行合理的划分,这样有利于实现对高阶攻击的保护.而利用带约束的强部分平衡t-设计构造分裂认证码的关键问题是:样本中任意t个元素恰好出现在所构造出来的区组中的λ个中,且这t个元素中的每一个又恰好分别出现在这λ个区组划分出来的不同的t个子区组中.
2 在有限域Fq 上的二维向量空间中构造分裂认证码
本节研究分裂认证码的构造.根据1.2 节所述,一个完善认证系统与一个带约束的强部分平衡t-设计有一一对应关系,也就是构造完善分裂认证码等价于构造一个带约束的强部分平衡t-设计.本文就是在有限域Fq上的二维向量空间中构造一个带约束的强部分平衡t-设计,从而由这种设计构造两个完善分裂认证码.下面给出分裂认证码的具体构造.
2.1 分裂认证码的构造I
在Fq上的二维向量空间中,利用线性方程组的知识,将

作为编码函数,常数变量λj用来实现可裂.
2.1.1 一种带约束的强部分平衡t-设计的构造
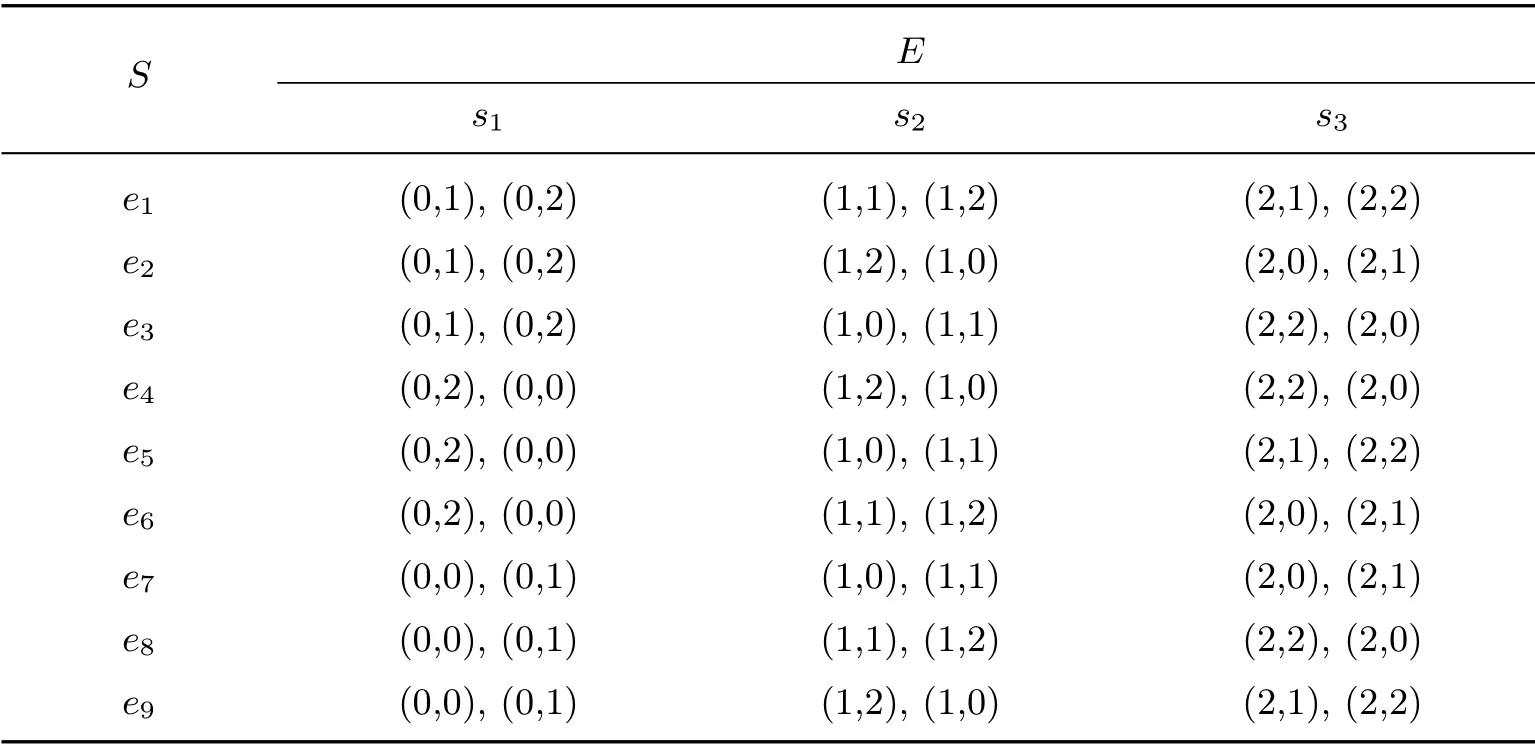
设Fq为含有q个元素的有限域,t为正整数且t < q,取样本集X为{(x,y)|x,y ∈Fq}.对Fq上的任意t元组(at−1,at−2,···,a0),取定任一λj ∈ Fq,定义区组为其中u=1,2,···,q;j=1,2,···,c,且满足c 记B为Fq上的任意t元组(at−1,at−2,···,a0)的集合,即为区组的集合,这样的t元数组数目为qt,即|B|=qt. 每一个区组Bi可以表示为互不相同的长度为c的q个子区组的并Bi=Bi1∪Bi2∪···∪Biq,其中 对于每一个区组B(at−1,at−2,···,a0),取Fq中t个互不相同的元素x1,x2,···,xt,对于M中任意t个点 它们满足 方程组(5)看作以at−1,at−2,···,a0为未知数的线性方程组,其系数矩阵为 显然,式(6)的行列式不为0.因此秩为t,故线性方程组(5)有唯一解,那么这t个点就被包含在由at−1,at−2,···,a0所定义的唯一区组里.根据Bi=Bi1∪Bi2∪···∪Biq的定义可知:(xu,yuj)恰好出现在Bi=Bi1∪Bi2∪···∪Biq的某个子区组Biu(=1,2,···,q)中.因此二元组(M,B)是一个RPBDt −(q2,qt,q×c;1,0). 对于M中的任意s(1st −1)个点, 如果它们在一个区组B(at−1,at−2,···,a0)中,则有以at−1,at−2,···,a0为变量的方程组 由于方程组(8)的系数矩阵中存在s阶范德蒙德矩阵,所以秩是s,从而该方程组刚好有qt−s个解,这就意味着|λs|=qt−s. 因此二元组(M,B)是一个RSPBDt −(q2,qt,q×c;λ1,λ2,···λt−1,1,0),其中λs=qt−s(1st −1). 2.1.2 分裂认证码的构造 本节研究目标是利用2.1.1 节中所构造的带约束的强部分平衡t-设计构造分裂认证码.设认证码的信源集合为S=Fq,消息集合M,编码规则的集合E分别为上述设计中样本的集合X和区组的集合B.对于每一个区组B(at−1,at−2,···,a0)和Fq中给定的λj ∈Fq ,可定义一个编码规则e ∈E,使得 因此,编码规则e的数目|E|取决于t元数组(a0,a1,···,at−1)的数目.这样的t元组数目为qt,即|E|=qt.由2.1.1 节可知:对任意s个消息有效的密钥数为|E(ms)|=λs=qt−s. 根据定理1,由2.1.1 节中所构造的 可以得到一类t-阶完善c-分裂认证码,其中信源数|S|=q,消息数|M|=q2,编码规则数|E|=qt.假设编码规则E和信源S具有一致分布,则有 通过消息(xu,yuj)就可以知道对应的信源xu,所以这个码是一个Cartesian 认证码.因此这个Cartesian 认证码是t-阶完善c-分裂认证码. 如果s=t,那么方程组(8)存在唯一的解,由定义6 可得,该码是I 型的完善认证码. 式中,u=1,2,···,q, j=1,2,···,c,满足c 对于每一个区组(at−1,at−2,···,a0),定义一个编码规则,使得 即一个信源xu被加密成消息(xu,yuj),j=1,2,···,c,编码规则的数目即为Fq中t元组(at−1,at−2,···,a0), at−10的数目.这样的t元组的数目为(q −1)qt−1,所以编码规则数目=(q −1)qt−1. 对于区组(at−1,at−2,···,a0), at−10,在Fq中取t个互不相同的元素x1,x2,···,xt,对于M中任意t个点 适合下列方程组 在方程组(16)中,未知量为at−1,at−2,···,a0.设 有|E(ms)|=qt−1−s(q −1). 故(M,B)是一个RSPBDt−(q2,(q −1)qt−1,q×c;λ1,λ2,···,λt−1,1,0),根据定理1,一 个新的t-阶完善c-分裂Cartesian 认证码可以被得到. 假定编码规则E和信源Sr满足等概率分布,可以得到 与构造I 类似,该码也是一个t-阶完善c-分裂Cartesian 认证码.根据定义6,该认证码是II 型的完善认证码. 在构造I 中,令q=3, c=2, t=2.由构造可知其中x ∈F3.λj分别取1 和2,信源S={s1,s2,s3}=F3.对应的设计为RSPBD 2-(9,9,3×2;3,3,10),所构造的分裂认证码的编码矩阵如表1所示. 表1 分裂认证码构造I 的编码矩阵Table 1 Coding matrix of splitting authentication code I 值得说明的是,当λj分别取0,1 和0,2 时,又会得到其他两种编码矩阵.根据构造,对于固定的λj,由编码矩阵也可看出,两种攻击成功概率都是.取λj=1,对编码矩阵进行数值仿真,结果如图1所示. 图1 编码矩阵仿真Figure 1 Coding matrix simulation 仿真分析:图1以信源S作为横坐标,编码函数e(s)为纵坐标.任意选取消息(0,2),通过图像可知,有三条线通过该点,即对消息(0,2)有效的编码规则数目为3,总的线数即为编码规则数目为9,从而模仿攻击成功的概率为;任意选取两个消息(0,2),(1,2),通过图像可知,只有一条线通过这两点,即对消息(0,2),(1,2)都有效的编码规则数目为1,从而替换攻击成功的概率为.通过仿真图像所得的结论与构造方案结果一致,故本文的构造合理可行. 在构造I 的基础上,要求a10可得到构造II,因此上例对应的构造II 的编码矩阵如表2所示. 值得说明的是,当λj分别取0,1 和0,2 时,又会得到其他两种编码矩阵.根据构造,对于固定的λj,由编码矩阵也可看出,两种攻击成功概率都是.取λj=1,对编码矩阵进行数值仿真,结果如图2所示. 表2 分裂认证码构造II的编码矩阵Table 2 Coding matrix of splitting authentication code II 图2 编码矩阵仿真Figure 2 Coding matrix simulation 仿真分析:图2以信源S作为横坐标,编码函数e(s)为纵坐标,任意选取消息(0,2),通过图像可知,有两条线通过该点,即对消息(0,2)有效的编码规则个数为2,此时编码规则个数为6,从而模仿攻击成功的概率为.任意选取两个消息,通过图像可知,只有一条直线通过这两点,即对消息(0,2),(1,2)都有效的编码规则个数为1,从而替换攻击成功的概率为.通过仿真图像所得的结论与构造方案结果一致,故本文的构造合理可行. 性能分析: 1)在上例中,将所构造的分裂认证码的相关参数与文献[15]中利用可裂设计构造的分裂认证码进行比较可知,在编码规则数目|E|=9 相同的前提下,本文的信源数目为3,大于文献[15]的信源数目2. 2)本文以线性方程组的理论为基础,构造了带约束的强部分平衡设计,与文献[15,21-23]相比,构造方法相对简单易懂,编码复杂度较低. 4)本文将文献[8]中关于完善认证码的构造推广至完善c-分裂认证码,即本文所构造的分裂认证码满足|E|=(P0P1···Pt−1)−1,达到了组合论中完善的界. 本文主要利用有限域上二维向量空间,借助线性方程组的理论,构造了带约束的强部分平衡设计,在强部分平衡设计的基础上构造了两类t-阶完善c-分裂认证码. 优点主要体现在三方面:1)用线性方程组求解等简单的理论知识使编码算法相对简单,复杂度较小;2)在编码规则数目相同的前提下,本文的信源数目大于文献[5]的信源数目,有利于提高信息传输的效率;3)认证码的各阶攻击成功概率均达到了最小,且满足完善性的条件,从信息安全性的角度来看,也是较好的. 不足主要体现在两方面:1)在构造组合设计时样本选择的条件可以更严谨一些,在后续的研究中将继续进行改进;2)Cartesian 认证码对信源不具有保密性,用类似方法构造对信源具有保密功能的非Cartesian 认证码,在后续的研究中将继续进行探索.
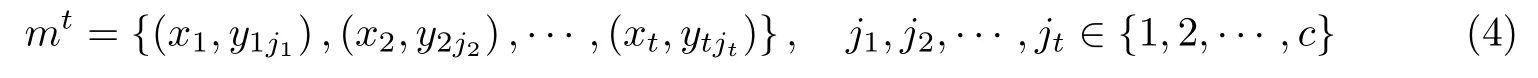
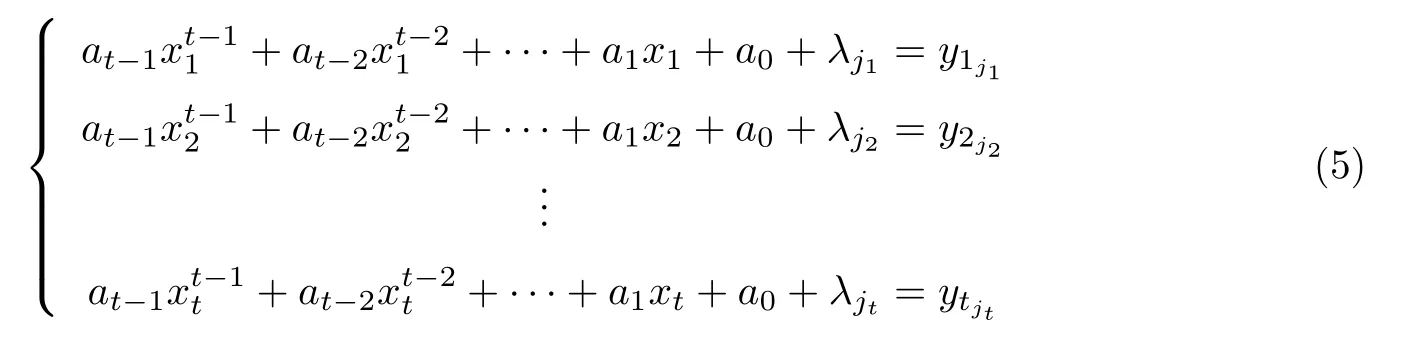




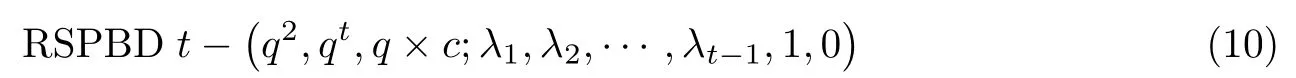

2.2 分裂认证码构造II
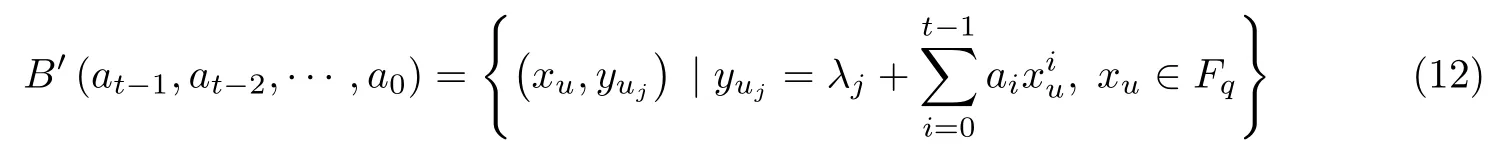


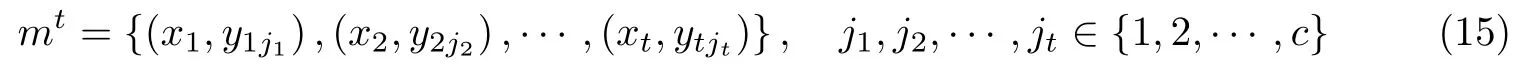
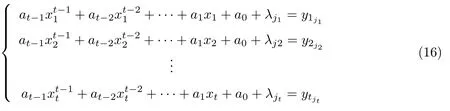



2.3 实例验证和性能分析



3 结 论
——平衡不完全区组设计定量资料一元方差分析

