基于快速特征欺骗的通用扰动生成改进方法

韦健杰，吕东辉，陆小锋，孙广玲

上海大学通信与信息工程学院，上海200444

近年来，深度神经网络已经被广泛应用于图像分类[1]、目标检测[2]和自然语言处理[3]等领域.然而网络的输出非常容易受到输入端微小扰动的影响，如果把特定算法生成的微小扰动添加到图像上，容易使网络输出错误的结果[4].这种以攻击性为目的的扰动称为对抗扰动[5].对抗扰动已经对人工智能系统的安全性和可靠性构成严重威胁，例如在交通指示牌上添加了刻意设计的贴纸，容易使自动驾驶的汽车错误地识别交通标志信号，因而导致重大的交通事故.除此之外，对抗扰动具有跨模型攻击能力，可以通过已知模型进行训练优化以实现对未知模型的攻击[6].因此，深入研究对抗扰动的存在根源和生成方法，对构建安全可靠的人工智能系统至关重要.

面向深度神经网络生成对抗扰动的研究成果较多，包括快速梯度符号法[7]、基本迭代法[8]、CW攻击法[9]和深度欺骗法[10]等，这些方法只针对单幅图像和单个网络模型生成对抗扰动，效率不高.文献[11]基于深度欺骗法针对特定的样本集和特定的网络模型，生成了一幅可作用于所有输入图像并且可以将攻击成功迁移到其他网络模型上的通用扰动图像.文献[12]提出了快速特征欺骗（fast feature fool, FFF）方法，该方法不必学习图像数据，在仅知网络模型内部结构和参数的情况下即可生成通用扰动.文献[13]在FFF 方法的基础上引入了数据集的信息，提出了通用扰动生成方法的一个系列.该系列共包含3 种方法：数据无关的特征欺骗方法；基于统计特征的特征欺骗方法；基于输入样本的特征欺骗方法.

在对抗扰动的防御方面，文献[14]考虑到自然图像的特殊属性，如像素的空间相关性和高频中的低能量性，提出了利用图像预处理的方法如滤波器滤波来去除扰动的干扰.文献[15]用对抗训练的方法来提高神经网络的鲁棒性，将添加扰动后的对抗样本重新输入到神经网络中进行训练，从而降低错误率.文献[16]提出集成对抗训练方法，将用于固定预训练模型的干扰添加到训练数据中来提高训练效果.文献[17]提出网络蒸馏法，将第1 个神经网络输出的分类结果输入到第2个网络中进行训练以降低模型对小扰动的敏感度，从而提升模型的鲁棒性[17].

研究基于FFF的通用扰动生成方法时发现，与基于深度欺骗法的通用扰动生成方法相比，前者有着攻击成功率更高、训练时间更短及迁移攻击效果更好的优点，它们都通过最大化卷积层输出特征的方式来实现攻击，可以认为是简单有效地增大对抗图像与原始图像之间特征差异的方法.然而，如果原输入图像在某一层的输出特征大到接近饱和时，该方法就无法达到欺骗神经网络分类器的目的.另外该方法将所有卷积层的输出特征以相同权重求和，没有考虑不同卷积层对于生成扰动的不同影响.事实上，网络模型中往往存在少数可以对预测结果造成较大影响的卷积层，只要攻击这些卷积层就可以提高扰动的攻击效率.

针对卷积层输出特征最大化的问题，本文不再通过最大化卷积层输出特征的方式来训练扰动，而是注意到输入图像在网络中的实际激活状态，寻求对抗图像与原图像在各卷积层输出特征之间差异的最大化.针对各卷积层权重相同的问题，本文将考虑不同卷积层对于生成扰动的不同影响，在损失函数中对不同卷积层附以不同权重.针对不同的图像分类网络模型进行攻击可以说明，改进后的方法更加有效，也具备了更强的迁移攻击能力.

1 快速特征欺骗

快速特征欺骗是一种基于梯度下降的迭代优化算法，其原理如图1所示.该方法提取网络模型各卷积层的输出特征，通过最大化各卷积层的输出特征之和来优化网络模型的输入，最后生成一幅可以对神经网络模型的特征提取造成最大影响的通用扰动图像.该系列一共包含3种方法，下面分别加以介绍.

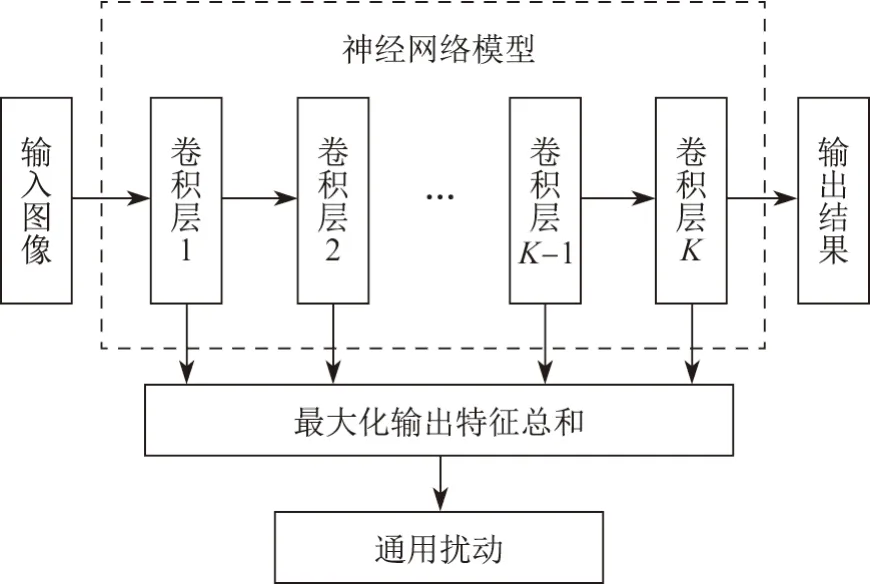
图1 FFF 原理框图Figure 1 Diagram of FFF

1.1 数据无关的特征欺骗方法

该方法无需任何图像数据，仅将随机初始化扰动输入到网络模型中进行训练.设δ为对抗扰动，ξ为扰动的最大强度，li(·)是网络第i层卷积层的输出，K为被攻击的层数，则该方法的损失函数为

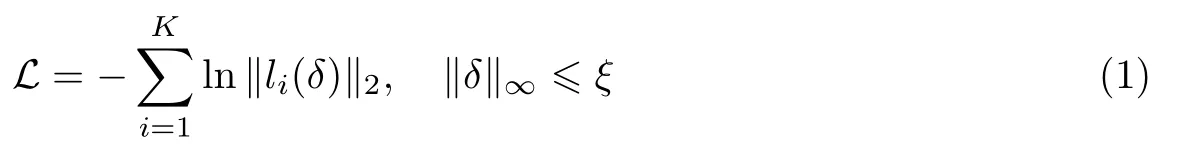
1.2 基于统计特征的特征欺骗方法

该方法预先生成一幅呈现高斯分布的伪数据样本，其均值为图像数据集的均值，并为其指定方差使得绝大多数采样点都在0∼255 范围内，然后将此样本和随机初始化扰动叠加，输入到网络模型中进行训练.伪数据样本具有与数据集相同的统计特性，可以为扰动的生成提供方向.该方法的损失函数为

式中，d为呈现高斯分布的伪数据样本.

1.3 基于输入样本的特征欺骗方法

该方法将图像数据集中的原始图像和随机初始化扰动叠加，输入到网络模型中进行训练.与1.2 节中基于统计特征的特征欺骗方法不同的是该方法直接使用了真实的图像数据，因此扰动的训练更具有针对性，其损失函数为

式中，x表示原始图像样本.

2 改进的快速特征欺骗

在第1 节中介绍的3 种方法存在以下问题：1）它们都以最大化对抗样本在各卷积层的输出特征为目标对扰动进行优化，从而造成对抗样本和原始图像在对应卷积层上的特征差异，但输出特征不可能无限增大，当原始图像的输出特征足够大时，该方法无法达到欺骗神经网络分类器的效果.2）各卷积层的输出特征以相同权值相加，而神经网络不同卷积层的输出特征是有差异的，简单求和的方式无法体现各卷积层之间的差异.针对以上两个问题，本文在FFF 系列3 种方法的基础上进行改进，下面加以介绍.

2.1 改进的FFF 原理

改进的FFF原理如图2所示.1）采用特征差异最大化的方式代替原本特征最大化的方式，将原始图像和对抗样本分别输入到网络模型中，计算原始图像和对抗样本在对应卷积层的输出特征差异.2）考虑不同卷积层之间的差异，采用各卷积层加权求和的方式代替各卷积层的简单求和，对网络输出结果影响较小的卷积层给予较低的权重，而对网络输出结果影响较大的卷积层则给予较大的权重，图2中的α1、α2、αK−1和αK分别表示卷积层1、卷积层2、卷积层K −1 和卷积层K的权重.最后以最大化该特征差异总和为目标进行优化得到通用扰动.

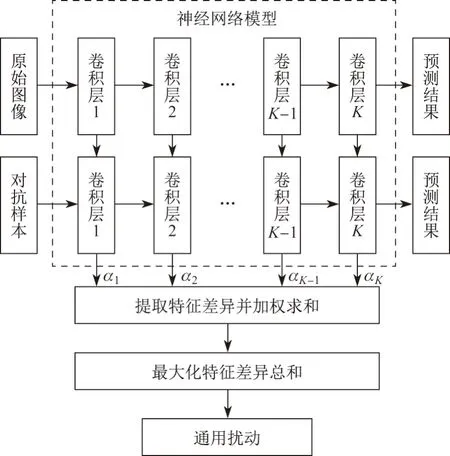
图2 改进的FFF 原理框图Figure 2 Diagram of improved FFF

基于原理框图可将改进方法的损失函数设计为

式中，li(x+δ)−li(x)为对抗样本和原始图像在第i层上的特征差异，αi为第i层输出特征的权重，并且所有权重之和为1.经实验发现，卷积层层数越高对网络模型输出结果的影响越大，于是采用权重逐层递增的规则设置权重.卷积层权重与其对应的层数满足如下关系：

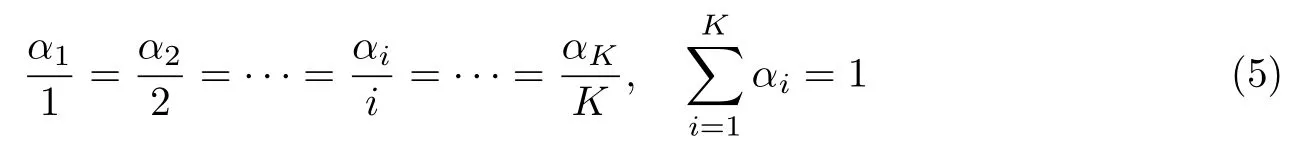
2.2 通用扰动生成过程

通用扰动生成的流程图如图3所示，其中Sati表示扰动在第i次迭代时的“饱和度”，即扰动图像中达到扰动最大强度ξ的像素的比率，SatCi表示前后两次迭代“饱和度”的变化率.首先随机初始化扰动，根据式(4)计算当前损失函数并对扰动进行更新，每次迭代完成后计算当前的Satt和SatCt，当Satt >0.5 且SatCt <0.000 01 时，认为训练达到了“饱和状态”.在验证集上对此时的扰动进行测试，如果新的扰动在验证集上能够得到更高的欺骗率，则覆盖之前的结果并保存此时的扰动.然后将扰动大小压缩至原来的一半，继续训练，直至到达下一个“饱和状态”或最大迭代次数，即可得到通用扰动.

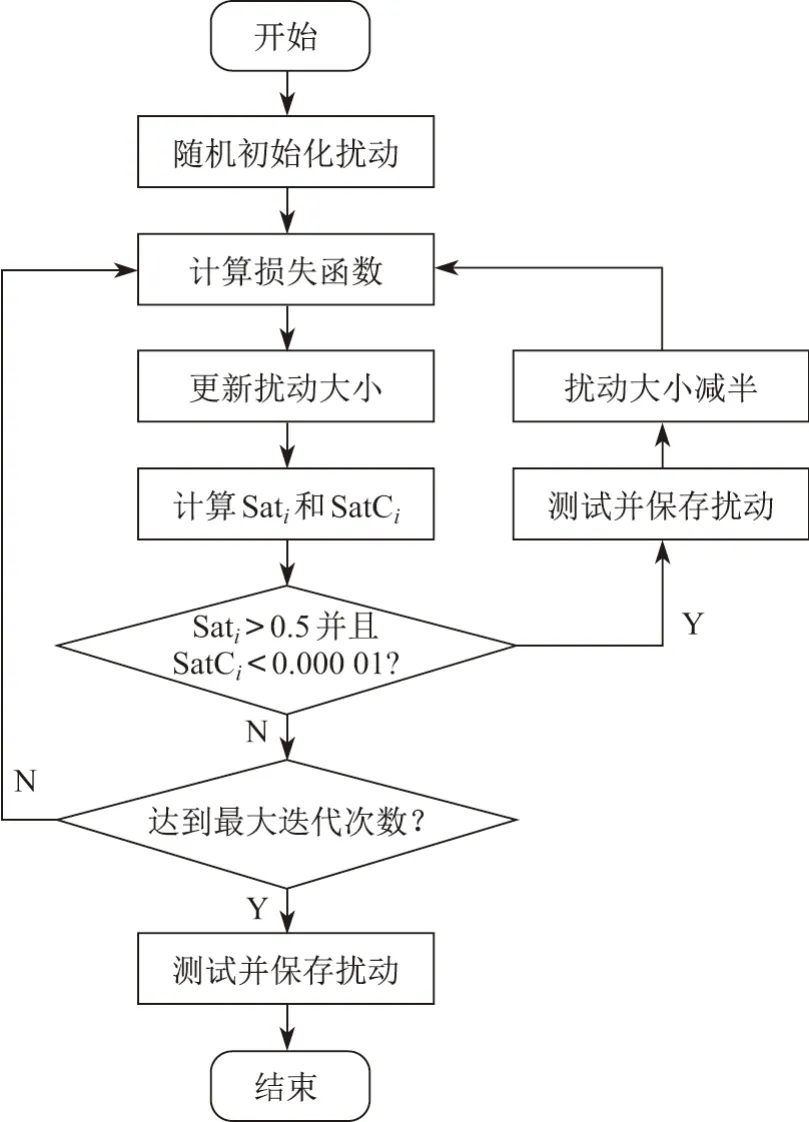
图3 通用扰动生成流程图Figure 3 Flow chart of crafting universal perturbations

3 实验结果及分析

3.1 实验设置

本文选取图像分类任务中比较经典的5 个网络模型作为本次实验的目标攻击模型，这5个网络模型分别是Caffenet、Vggf、Vgg16、Vgg19和Googlenet，并且预先在ILSVRC 图像数据集中训练完成.在通用对抗扰动训练过程中，将学习率（learning rate, LR）设置为0.1，将最大迭代次数设置为40 000；扰动强度可设置为10，即扰动图像上每个像素点的值在[–10,10]之间.

实验使用PC 的硬件配置为Intel core i7-8750H 处理器、NVIDIA GTX1060 独立显卡、16GB 内存；软件配置为python3.7 版本、pycharm 开发环境、pytorch＆tensorflow 深度学习框架.

3.2 改进的快速特征欺骗的实验结果

采用改进的FFF 方法分别针对5 个不同的网络模型训练生成通用扰动，结果如图4和5 所示.图4为改进的FFF 方法训练生成的通用扰动示意图，对应的网络模型标注在图像正下方.可以观察到：在不同网络模型下训练生成的通用扰动有着不同的视觉纹理特征，同一扰动的纹理特征则呈现出一定的规律性.图5为添加了本文生成的通用扰动的对抗样本与其对应的原始图像的主观视觉差异对比，其中第1 排代表原始图像，第2 排代表对抗样本，图5(f)∼(j)的图名为Googlenet 网络模型对图像的预测结果.此时人的肉眼几乎无法辨别对抗样本和原始图像之间的视觉差异，而网络模型却对所有的对抗样本给出了错误的分类结果，说明了改进方法所生成的通用扰动在满足扰动的视觉不可感知性的同时能够达到欺骗网络模型的效果.

图4 改进的FFF 生成的通用扰动Figure 4 Universal perturbations crafted by improved fast feature fool

3.3 相关方法性能比较

在图像分类任务上，通用扰动的攻击效果的评价指标为欺骗率（fooling rate, FR），FR 表示添加通用扰动后会造成模型分类错误的图像占整个测试集图像数的比例，FR 越高，说明通用扰动的攻击效果越好.

本文在已有的FFF 系列方法上进行了两点改进，即考虑特征差异最大化和考虑层间差异.将本文方法与只考虑特征差异最大化的改进方法、只考虑层间差异的改进方法以及快速特征欺骗系列的3 种方法进行比较，采用上述6 种方法分别针对5 个不同的网络模型进行训练，共生成30 幅通用扰动图像，在包含50 000 幅图像的测试集上对扰动的攻击效果进行测试并对比统计FR 值，实验结果如表1所示.

在表1中，第1 行为扰动训练及攻击的网络模型，第1 列为扰动生成方法.对比前3 行已有方法可知，数据信息的引入能在一定程度上提升通用扰动的FR 值，数据信息引入得越多，FR值越高，通用扰动的攻击效果就越好.另外只考虑层间差异的改进方法和只考虑特征差异最大化的改进方法的FR 值在5 个不同的网络模型上均高于已有的3 种方法，说明本文提出的两点改进措施都是有效的.最后，本文方法同时考虑了两点改进，其FR值相较于已有表现最好的基于输入样本的特征欺骗方法，平均提升了5.3%.

图5 原始图像和对抗样本的主观视觉差异对比Figure 5 Comparisons of subjective visual difference between original images and adversarial samples

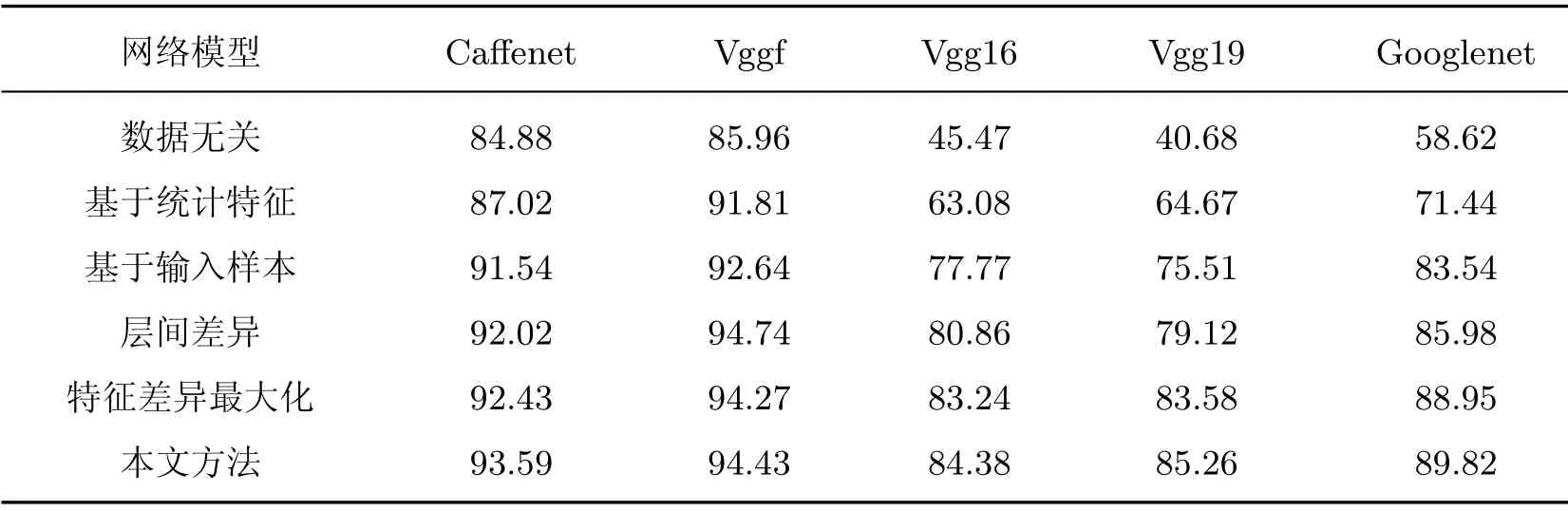
表1 不同策略FFF 的欺骗率Table 1 FR of FFF using different strategies

3.4 跨模型性能比较

为了进一步说明本文方法的有效性，将本文方法与已有表现最好的基于输入样本的特征欺骗方法的跨模型攻击效果进行比较，结果如表2∼4 所示.

在表2和3 中，列代表扰动生成网络，行代表目标攻击网络，Average 表示攻击5 个网络模型的平均欺骗率.由表2和3 可知：对于绝大部分通用扰动来说，攻击自身的成功率高于攻击其他模型的成功率，说明了白盒攻击能力总是强于黑盒攻击能力.表4对比了两种方法的平均跨模型欺骗率，因为Caffenet 网络结构简单，且与其他网络模型之间结构差异较大，所以改进方法的跨模型攻击效果并没有得到明显的提升.然而，在其他4 个网络模型中，本文提出的改进方法在跨模型攻击效果方面明显优于FFF 系列中基于输入样本的特征欺骗方法，进一步验证了本文方法的有效性.

表2 基于输入样本的特征欺骗方法的跨模型欺骗率Table 2 Cross-model FR of FFF using input samples %

表3 本文方法的跨模型欺骗率Table 3 Cross-model FR of the proposed method %

表4 平均跨模型欺骗率对比Table 4 Comparisons of average cross-model FR %

4 结 语

FFF 系列的3 种通用扰动生成方法的不足之处在于：1）没有考虑添加扰动后的输出特征与原始图像输出特征之间的差异.2）没有考虑不同卷积层之间输出特征的差异.对此，本文提出了一种基于FFF 的通用扰动生成改进方法，在特征差异最大化和层间差异两方面对原有方法进行改进.实验表明，本文提出的改进方法相较于原有方法，其扰动攻击成功率有了较大提升，并且改进方法在图像分类任务的不同网络模型之间具有良好的迁移攻击能力.

本文提出的改进方法目前仅仅在图像分类任务上被证明是一种高效的通用扰动生成方法，尚不能证明该方法在其他计算机视觉任务中也具备良好的攻击效果.未来工作还可以结合其他计算机视觉任务如语义分割和目标检测等展开研究，以探究该方法的通用性.