基于EMD优化NAR动态神经网络的地铁客流量短时预测模型
马飞虎,金依辰,孙翠羽
华东交通大学土木建筑学院,江西南昌330013
随着城市化进程的飞快推进,城市交通堵塞现象越来越严重.大力推进公共交通的蓬勃发展是舒缓城市拥堵压力的有效方法.地铁作为城市主要公共交通工具之一,因其准点率高、运量大等特点受到广泛青睐,但地铁站客流量过于饱和的情况也时有发生.为了更加合理地进行车辆调度和制定人员配置方案,并在满足人们出行需求的基础上实现资源利用最大化,准确的地铁客流量短时预测是非常必要的[1-2].
目前地铁客流量的短时预测是一个研究热点,很多学者运用了不同的方法构建模型从而进行客流量预测研究.文献[3]采用了自回归滑动平均(auto-regressive moving average,ARMA)时间序列模型对地铁的客流量进行预测,结果表明ARMA 模型较适用于平稳的客流量数据,当客流量受外界因素(如天气、周末、节假日等因素)影响发生较大变化时,ARMA 模型会出现较大的预测误差;文献[4]提出了基于卡尔曼滤波算法的轨道交通短时换乘客流预测模型,但该模型对突变点的预测精度不达标,且部分预测结果存在时滞问题;文献[5]应用Elman 神经网络预测模型进行了地铁短时客流预测,研究显示,该模型针对含有非线性特征的地铁客流数据的短时预测有良好效果.
神经网络因其具有可探索数据间的复杂关联、拥有良好的数据处理能力、对样本数据的质量要求较少、运算灵活机动的特点在数据处理与运算方面广泛使用[6].由于地铁客流数据具有非平稳非线性且有时序性的特点,本文选用NAR 动态神经网络算法进行客流预测.
1 NAR 动态神经网络
NAR 神经网络基于NAR 非线性自回归模型,以自身作为回归变量,通过一段时间内的随机变量的线性组合来表示之后某一时刻的随机变量.作为一种基于时间序列的动态神经网络,其输出不只是一种静态映射,还是之前动态结果的综合利用,因此具有反馈与记忆功能[7-8].NAR 神经网络模型可以描述为
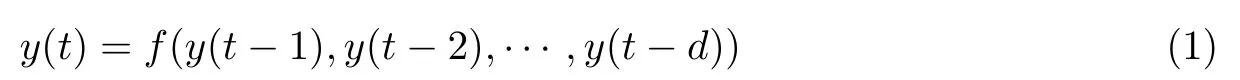
式中,y(t)为当前时刻的输入值,y(t −1),y(t −2),···,y(t −d)为历史时刻的输出值,d为延迟阶数.
NAR 动态神经网络一般由输入层、时滞层、隐藏层与输出层构成,如图1所示,数据y(t)从输入层输入,经过时滞层和隐藏层进行处理、训练、学习,最后由输出层输出预测结果.其中y(t)为输入数据,为输出数据,1∶4 为延时阶数,W为连接权值,b为阈值.

图1 NAR 神经网络Figure 1 NAR neural network
2 EMD 经验模态分解算法
经验模态分解(empirical mode decomposition, EMD)是一种可以处理非线性和非平稳数据的信号分析算法.该算法是根据数据本身的时间尺度特征对一组信号进行分解,其核心思想是把一组复杂信号中的不同波形分解成若干个分量,这些分量包含了原始序列中不同特征尺度的本征模态函数(intrinsic mode function, IMF).与原始信号对比,IMF 本征模态函数表现出更加平稳的特征[9-10].EMD 经验模态分解处理结果如图2所示.

图2 EMD 分解Figure 2 EMD decomposition
与其他数据预处理方法不同,EMD 算法在分解过程中并不改变原始数据的属性,即所有原数据拥有的特性都会被保留下来,而且每个分量都可以体现出原始数据的部分特性.因此,EMD 算法适用于各种类型的信号分解,在非平稳与非线性的数据处理上优势突出,信噪比较高.
3 EMD-NAR 组合客流预测模型
从预测的角度来讲,短时地铁客流预测在时间维度上具有不同的特性,在不同时间会有不一样的走势.一个好的预测模型要综合工作日特性、节假日特性、周特性、月特性等数据.地铁客流数据是非线性非平稳数据,在预测这类数据时,考虑到NAR 神经网络的特性以及EMD 方法的独特优势,结合NAR 动态神经网络良好的非线性动态表述能力和EMD 算法把复杂信号分解为更加平稳分量的特点,针对性地将两者融合在一起,提出EMD-NAR 神经网络组合预测模型[11-13],模型结构如图3所示.
EMD-NAR 神经网络组合模型的工作步骤如下:
步骤1EMD 分解,将原始的地铁客流量数据经EMD 算法分解成多个IMF 分量,使数据平稳化,降低原数据的波动性和复杂性;
步骤2分量重构,将IMF 分量根据其皮尔森相关系数进行分类整合,简化步骤且减少预测误差;
步骤3NAR 动态神经网络预测,把经过归一化处理的分量逐一输入到NAR 神经网络模型中进行训练、学习、预测;
步骤4输出结果,将NAR 神经网络预测出的数据分量进行整合,得到预测结果并输出.
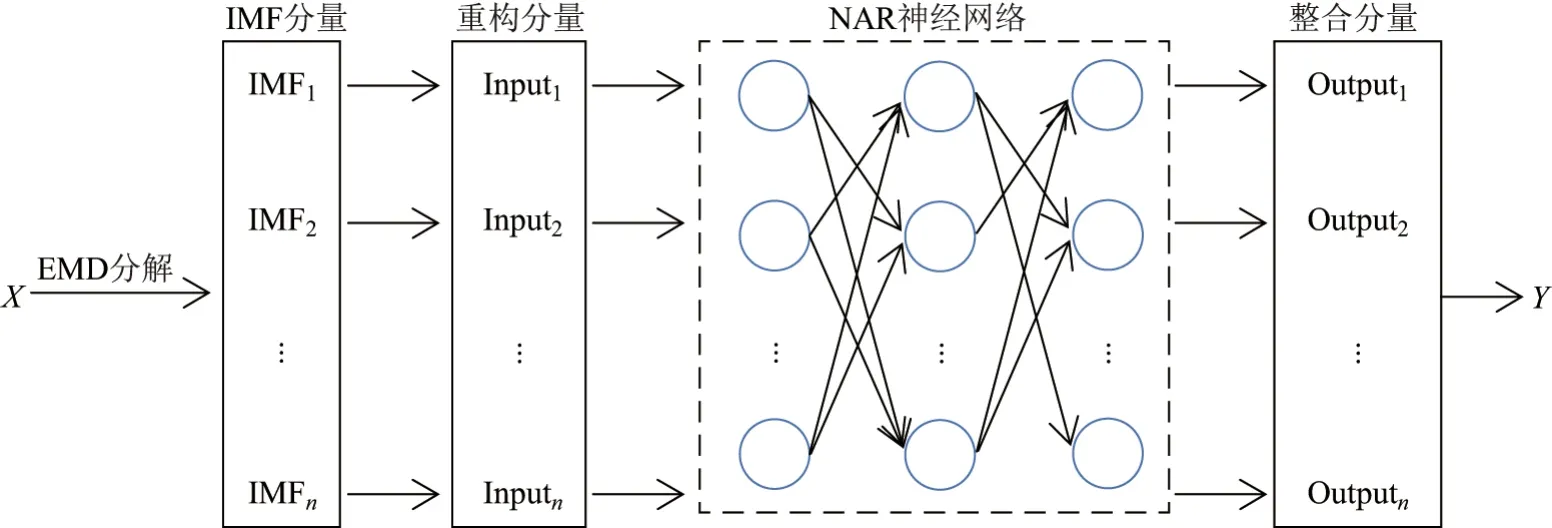
图3 EMD-NAR 组合预测模型Figure 3 EMD-NAR combined prediction model
4 预测实验与结果分析
4.1 基于EMD-NAR 组合模型的地铁客流量预测实验
本次预测实验在Matlab R2016a 平台上编程实现.以合肥地铁2018年1月1日—9月22日的265 组地铁总客流量数据作为训练模型的输入数据,以2018年9月23日—29日的7 组数据为验证数据,测试模型的预测精度.
建立EMD-NAR 神经网络组合预测模型,具体步骤如下:
步骤1确定输入数据,设置训练集、验证集和测试集,本次实验设置输入数据分配占比为训练集70%、验证集15%、测试集15%.
步骤2数据分解,利用EMD 算法处理输入的原始地铁客流量数据,获得IMF 分量集合,其中包含了6 个IMF 分量和1 个剩余分量.IMF 分量集合是由原始信号数据根据其自身时间尺度特征分解而得,不改变原始数据自身特性,因此IMF 分量数据之和即为原始signal 数据.分解后的各分量如图4所示.
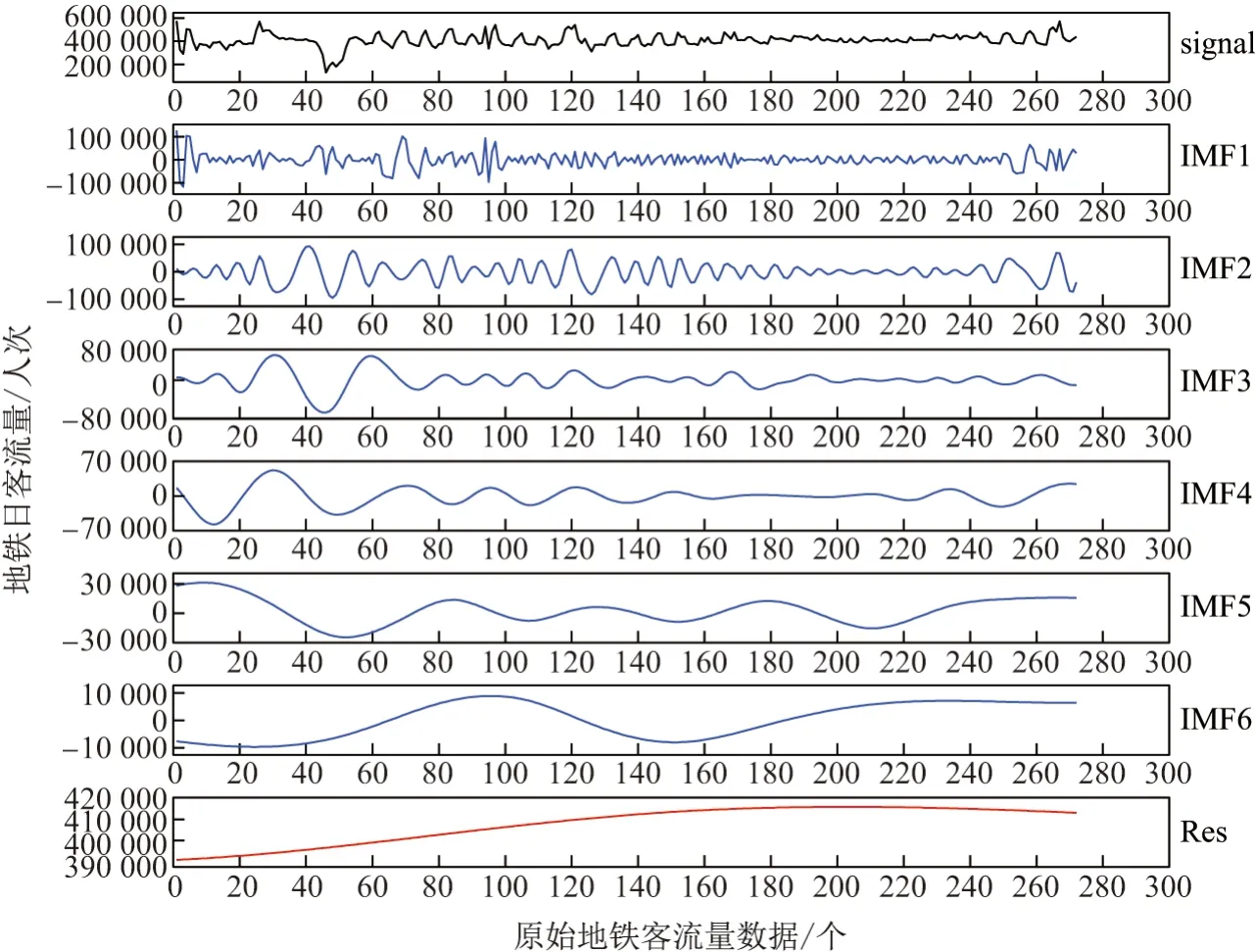
图4 地铁客流量的EMD 分解Figure 4 EMD decomposition of metro passenger flow
步骤3分量重构,根据皮尔森相关系数判断IMF 分量与地铁客流量数据之间的关联程度进行重构分量,关联结果如表1所示.

表1 皮尔森相关系数分析结果Table 1 Analysis results of Pearson correlation coefficient
从表1数据可以看出,地铁客流分量中IMF1、IMF2、IMF3和IMF4的相关系数较高,说明这些分量与原始地铁客流量数据的关联程度更大,而IMF5、IMF6、IMF7这3 个分量关联程度较弱.经验证,采用误差最小且操作较为简洁的分量重构方法,将关联程度大的分量代入Input1∼Input4分量并输入到NAR 神经网络进行预测,而关联程度较小的3 个分量相加重构为新的分量Input5输入神经网络.
步骤4数据归一化,为了降低源于输入信号之间的数量级差别过大导致预测结果误差增大的风险,需要对神经网络的输入信号进行归一化处理,将数据控制在[−1,1]之间.本文采用min-max 线性函数归一化法[14],公式为

步骤5构建NAR 动态神经网络,设定隐含层神经元数目,由于此数目无法通过具体数学公式计算获得,只能采用经验公式[15]进行选值参考,即

式中,m为隐含层的神经元数目,n为输入层的神经元数目,l为输出层的神经元数目,a为1∼10 之间的一个常数.以经验公式所得结果作为初始值,再采用试验法来不断调整数值以选取最合适的数值.经反复实验比较分析,本实验中不同分量对应的隐含层神经元设定如表2所示:

表2 不同分量对应的隐含层神经元数目Table 2 Number of hidden layer neurons corresponding to different components
步骤6训练神经网络,将归一化处理后的分量分别导入NAR 神经网络中训练、学习,NAR 神经网络模型的学习效果如图5所示,模型平均拟合误差约为6.63%.
步骤7预测结果导出,所得预测数据通过反归一化运算后重构生成最终预测结果.预测结果如图6所示.
4.2 预测结果精度评定
将7 组真实数据分别与使用NAR 神经网络模型预测和EMD-NAR 组合模型预测所得的数据进行比较,结果如图7所示.

图5 预测模型拟合结果Figure 5 Predictive model fitting results
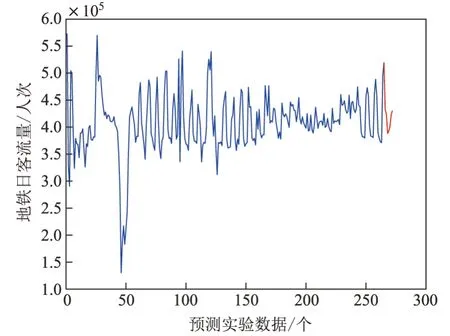
图6 预测结果输出Figure 6 Output of prediction results
选用均方根误差(root mean square error, RMSE)、平均绝对百分误差(mean absolute percentage error, MAPE)两项评判指标来判定模型的预测效果.公式为

结果如表3所示.

图7 预测结果与真实值对比结果Figure 7 Comparison of predicted results with real values

表3 模型预测效果Table 3 Effect of model prediction
RMSE 与MAPE 的值越小,说明预测结果的误差越小,预测值的精度越高.比较数次预测实验结果发现,EMD-NAR 神经网络组合模型的预测精度要优于单一NAR 神经网络模型.根据MAPE 值来判别预测精度,组合模型预测精度约达93%,满足对地铁客流量预测的精度要求.
5 结 语
本文对历史地铁客流量数据进行挖掘,针对其日客流变化规律特性设计了EMD-NAR 动态神经网络组合预测模型.对单一的NAR 神经网络预测模型而言,EMD-NAR 组合模型拥有更优的预测精度,且适用性较好.本研究在地铁的合理计划调度方案、安排人员配置、资源利用最大化等方面都具有积极意义,能为地铁的短时客流预测提供一种新的方法.地铁客流量受到很多因素的影响,具有高度不确定性,下一步的研究将考虑加入对时间、天气、节假日、特殊事件等影响因素,进一步提高客流预测精度.

