基于局部加权低秩先验的高光谱稀疏解混方法
黄 伟,伍飞扬,孙 乐
1.郑州轻工业大学计算机与通信工程学院,河南郑州450001
2.南京信息工程大学计算机与软件学院,江苏南京210044
高光谱图像(hyperspectral image, HSI)是由数十甚至上百个连续波段(通常小于10 nm)图像组成的三维数据立方体,其波段范围涵盖400∼2 500 nm,每个像元可以看成是连续的光谱曲线[1].由于具有丰富的空间光谱信息,高光谱遥感已在诸多领域中获得了广泛应用[2],如矿物勘探、环境监测、城市规划、食品安全、军事目标识别等.然而,受成像元件和复杂环境的影响,高光谱图像的空间分辨率普遍较低,图像中大部分像元包含多种地物的反射信息,使图像存在混合像元的现象[3].图像处理时通常采用光谱解混的方法,即通过反演图像中的端元及其对应的丰度系数来解决混合像元问题,可见解混是高光谱遥感图像后续应用的一个重要基础.
高光谱解混可分为线性光谱解混[4]与非线性光谱解混[5].与非线性光谱解混模型相比,线性光谱解混模型具有简单、高效以及物理意义明确的优点,该模型假设高光谱图像中的每个像元光谱都由端元光谱线性组合而成.传统的基于线性混合模型(linear mixture model,LMM)的解混方法首先进行端元提取[6],然后进行丰度估计[7]或者两者同时进行[8].
早期的线性光谱解混模型主要有几何方法与统计学方法[3],这些方法尽管只需高光谱图像数据少量的先验知识,但要假设场景中包含纯净的像元(即“端元存在假设”),如顶点成分分析方法(vertex compoent analysis, VCA).然而,受空间分辨率限制,这一假设在很多数据集中并不成立.一些研究人员也提出一系列“端元不存在假设”方法[7],但这些方法在高度混合或噪声较强的高光谱数据中表现较差.于是有学者提出了非负矩阵分解的方法(nonnegative matrix factorization, NMF)[8-9],该方法能够同时反演得到端元矩阵和丰度系数,但受制于模型的非凸性,该方法通常需要增加较为复杂的端元约束和丰度系数约束条件,使模型的收敛速度相对较慢.
近年来,随着稀疏表示与压缩感知理论的不断发展,以及美国地质调查局(United States Geological Survey, USGS)光谱库的出现,高光谱图像的稀疏解混方法越来越受到学者的关注[10].稀疏解混模型的优点是不需要进行端元提取,而是直接利用已知光谱库中的光谱信号构成端元矩阵,就能反演出丰度系数.由于光谱库中的光谱特征曲线数目远远大于真实场景中端元的数目,每一混合像元光谱曲线在光谱库下的丰度系数向量是“稀疏的”[11].为了精确地反演出丰度系数,通常需要在稀疏解混方法中加入一些附加信息作为先验知识.例如:文献[12]提出了利用交替迭代思想的SUnSAL (sparse unmixing by variable splitting and augmented Lagrangian)算法,采用L1 范数对丰度系数的稀疏性进行刻画,并通过变量分离与增广拉格朗日乘子法求解模型,取得了一定的成效;此外,协同SUnSAL 解混算法[13](collaborative SUnSAL, CLSUnSAL)利用了丰度系数的行稀疏特性,采用L2,1 混合范数对丰度矩阵施加协同稀疏约束,能够比L1 范数更有效地刻画丰度矩阵的稀疏性质,但该方法在一个端元仅存在于局部的像元而不是整个场景的像元时效果不太理想;由于地物分布的局部连续性,文献[14]采用了局部协同稀疏算法来克服CLSUnSAL 的局限性.然而SUnSAL,CLSUnSAL 以及局部CLSUnSAL 等算法只考虑了光谱的稀疏性,而没有利用到高光谱图像的空间相关性.
为了进一步挖掘光谱的空间相关性,文献[15] 提出了基于全变差正则项的SUnSALTV(total variation regularized SUnSAL)算法,该方法利用各向异性全变差(total variation,TV)刻画相邻像元的局部平滑特性,取得了较好的效果,但其局限性在于可能会导致边缘区域过度平滑.在高光谱图像高度相似的区域块中,像元光谱特征之间的相关性与相应丰度向量之间的相关性是一致的,且这些丰度向量组成的丰度矩阵具有局部低秩性质[16],说明像元对应的丰度向量在该区域中具有高度的空谱相关性[17].近年来,高光谱图像的低秩性质已广泛应用于去噪、分类、解混等方面,并取得了较好的效果.
本文提出了一种基于局部加权低秩先验的高光谱稀疏表示解混方法(hyperspectral sparse unmixing based on local weighted low-rank prior, HSULWLrP).高光谱图像作为一种自然图像,在局部区域中相邻的像元包含相同物质的可能性非常高,因此该局部区域中的丰度矩阵可以用低秩性质来估计.针对每个局部图像块用加权核范数来促使该图像块保持低秩结构,同时使用行稀疏对光谱信息进行约束和TV正则化项来提取空间信息.本文算法在现有解混方法的基础上考虑了协同稀疏性和空间差异性,采用模拟数据集和真实高光谱数据集进行测试.与其他稀疏解混算法(SUnSAL, CLSUnSAL, SUnSAL-TV, J-LASU)进行比较的结果表明,本文算法能够更好地保持数据的细节信息,提升解混精度.
1 相关工作
1.1 高光谱线性解混
在线性混合模型中假设每个像元光谱可以由像元中存在的所有端元光谱线性组合而成[3],则每个像元的线性模型可以描述为
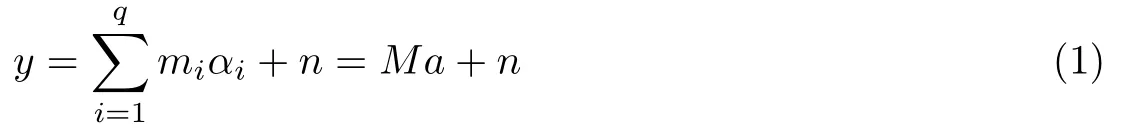
式中:y ∈Rl×1是一个l波段的列向量,表示混合像元;M ∈Rl×q是含有q个端元的光谱矩阵;a ∈Rq×1表示该像元对应的丰度向量;n ∈Rl×1是在观测过程中所产生的误差和噪声.
考虑到丰度系数的物理意义,在线性混合模型中引入了丰度非负限制(abundance nonnegative constraint, ANC)和丰度系数和为一的限制(abundance sum-to-one constraint,ASC)条件[4],分别表示为
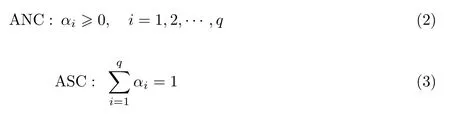
在一个高光谱场景中,Y ∈Rl×s为观测的高光谱图像数据,X ∈Rq×s为丰度矩阵,s是场景中的像元总数,则式(1)还可以表示为

式中,N ∈Rl×s为噪声和模型误差.
1.2 稀疏性解混
稀疏性解混模型假设用一个已知的光谱库A ∈Rl×t代替端元矩阵,t为光谱库A所包含的地物光谱数目,则线性混合模型可以改写为

式中,X ∈Rt×s为光谱库A对应的丰度矩阵.
一个高光谱图像中所包含的端元光谱数量远小于光谱库A中的地物光谱数量,因此丰度矩阵X中包含很多的零值,即丰度矩阵是强稀疏的.稀疏解混模型可以表示为

式中,||AX −Y||2F为模型的重构误差,为丰度矩阵X的Frobenius 范数,||X||0表示丰度矩阵X的L0 范数,即X中非零元素的数目.
因为L0 范数是非凸的,所以式(6)的最小化问题是一个NP-hard问题[11],求解比较困难.目前有理论证明,当光谱库矩阵A满足有限等距性质(restricted isometry property, RIP)条件时[11,13],L0范数问题可以等价转换为L1 范数的凸优化问题,即
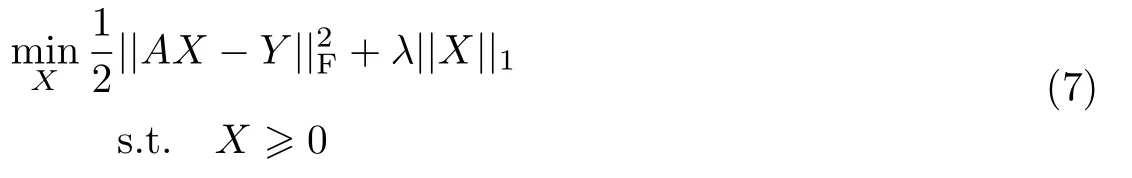
1.3 协同稀疏正则项
在实际的解混中,光谱库A足够大,场景中的端元数必然远小于光谱库A中地物光谱数量,因此丰度矩阵从全局上体现出行稀疏的特性,这意味着丰度矩阵X仅有少量的行有非零值,行稀疏性比L1 范数具有更强的稀疏性,于是CLSUnSAL算法用混合范数代替L1 范数得

1.4 空间正则项
式(6)∼(8)只从丰度系数的稀疏性角度考虑了解混问题,而实际上除了利用光谱体现出的性质之外,考虑空间信息也有利于提升解混结果.高光谱图像中的相邻像元通常包含相似的物质,这些像元间的光谱特征是相似的,而这种相似性通常表现为丰度系数间的分片平滑性,因此,文献[15]在式(7)的基础上提出了利用总变差TV 这一正则项来刻画空间信息,模型表示如下:


式中代表各向异性TV,用于促进相邻像元间平滑过渡,λ0 与λTV0 都是正则化参数,ε表示图像中水平和垂直相邻像元的集合.
令Hh: Rr×s →Rr×s,Hv: Rr×s →Rr×s分别表示丰度矩阵中相邻像元的水平和垂直差分线性算子[21-22],HhX=[d1,d2,···,dn],计算X的每个分量与其水平相邻像元的差分,即di=xi −xih,ih代表像元i的水平相邻像元.同理,HvX=[v1,v2,···,vn]为垂直差分算子,其中vi=xi −xiv,iv代表该像元i的垂直相邻像元.通过水平和垂直这两种运算可得
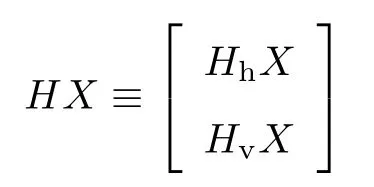
因此,式(9)又可以写为

与模型(7)相比,模型(11)同时考虑了光谱稀疏性和丰度系数在空间域上的分片光滑性,能够取得更精确的解混结果.然而,以TV 刻画的局部光滑性具有一定的局限,如对于边缘的刻画不够准确,容易导致过平滑现象.因此,迫切需要更精确的先验信息来挖掘丰度系数在空间分布上的细节信息.同时,如果能考虑更强的稀疏性,如加权L2,1 范数来刻画行稀疏性,将使得解混结果更加精确.
2 本文方法
2.1 加权低秩正则项

对局部丰度矩阵使用加权核范数来保持低秩,设中共有R个奇异值,则加权低秩正则项可以表示成

式中,||X||w,∗是矩阵X的加权核范数,w=[w1,w2,···,wR]T为矩阵X中R个奇异值对应的权重向量且wr0(r=1,2,···,R),σr()是的第r个奇异值.
一般地,局部块的丰度矩阵的奇异值大,说明该奇异值是该局部块丰度矩阵的主成分.在解混的过程中,应尽可能多衰减较小的奇异值而少衰减较大的奇异值,因此第p个奇异值的权重wr应该与奇异值成反比,即

式中,c>0 是一个常数,ε=10−16用来保证分母不为0.

式中,Sw(Σ)表示在权重w下的软阈值函数.
2.2 本文提出的模型及算法
在稀疏解混模型的框架下,本文方法添加了协同稀疏、TV、局部低秩这3 个正则项,称为HSULWLrP 模型,可以表示为
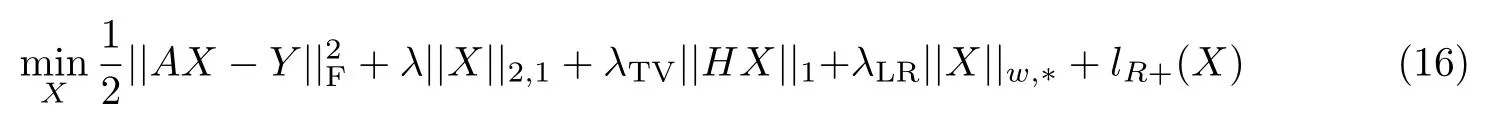
式中,λ,λTV,λLR分别是协同稀疏、TV、加权局部低秩这3 个正则化项的参数;lR+(X)是一个指示函数,当x0 时,lR+(X)=0;在其他情况下,lR+(X)=+∞,用来保证丰度非负限制这一先验条件.
直接求解式(16)比较困难,于是本文采用交替方向乘子法(alternating direction method of multipliers, ADMM)方法[12]来迭代求解,其核心思想是通过引入一些新的变量,可以把一个难以求解的问题转化为几个容易求解的子问题,对于这些子问题,逐个进行求解,相互交替进行更新.首先,引入变量V1,V2,V3,V4,V5,V6,则式(17)可以转化成

式(17)的拉格朗日函数为

式中,D1,D2,D3,D4,D5,D6为拉格朗日乘子,µ为拉格朗日惩罚因子.
算法1 给出了HSULWLrP 求解过程的伪代码,在ADMM 算法的每次迭代中,按顺序优化X,V1,V2,V3,V4,V5,V6,然后更新拉格朗日乘子,当满足停止条件时结束迭代.

接下来将讨论算法1 中第3 行的解,该步骤用于计算每次迭代过程中变量X的值.关于步骤3 的优化问题可以写成

式(19)的解为

算法1 中第5 行用来计算每次迭代过程中变量V1,V2,V3,V4,V5,V6的值.V1的优化问题可以写为

其解为

V2的优化问题可以写为

V2的解可以用著名的vect-soft threshold[13-14]函数得到
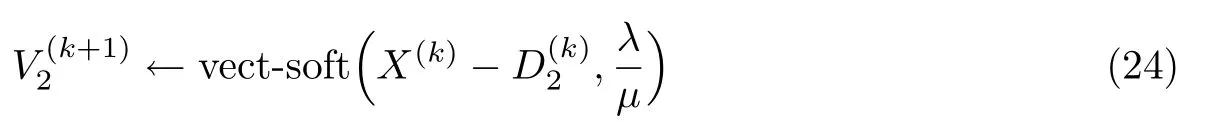
式中,vect-soft(·,τ)表示向量软阈值(vect-soft threshold)函数,可由(max{||y||2−τ,0}/max{||y||2−τ,0}+τ)求得.
V3的优化问题可以写为
性质II. GMC与Pearson相关系数rXY之间存在一定关系,当rXY=±1时,GMC(Y|X)=GMC(X|Y)=1;当rXY≠0时,GMC(Y|X)≠0,GMC(X|Y)≠0;当GMC(Y|X)与GMC(X|Y)二者其一为零时且
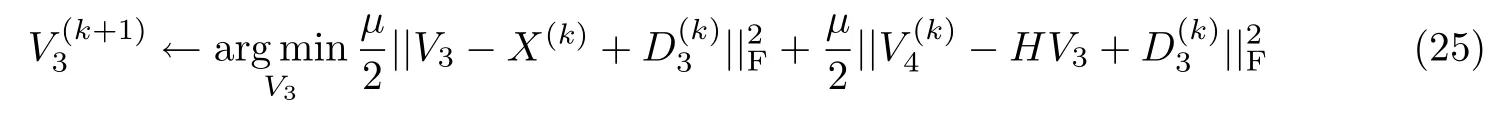
其解为

式中,H为差分算子,相当于卷积运算,仅作用于空间域,并且可以逐个光谱波段独立应用.
V4的优化问题可以写为

V4的解可以由软阈值(soft threshold)得到
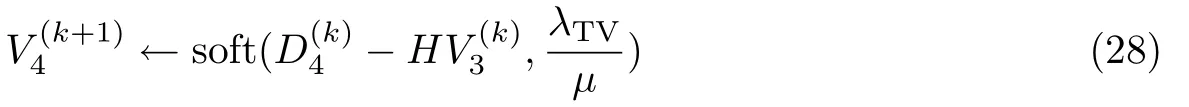
V5的优化问题可以写为

对于每个图像块的丰度矩阵,采用加权核范数最小化,然后输出重建的丰度矩阵.V5的解可以表示成
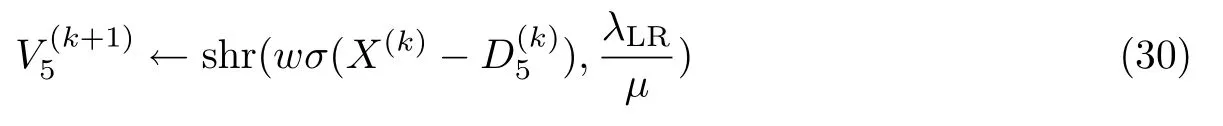
式中,shr(·,τ)表示的奇异值收缩函数diag(max{SVD(y)−τ,0}).
最后,V6的优化问题写为
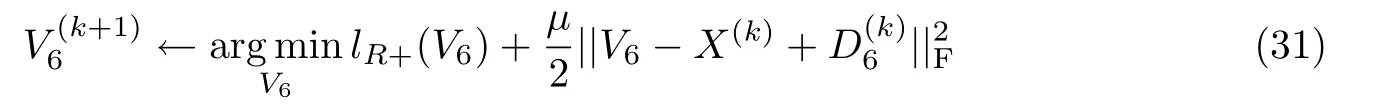
V6的解为
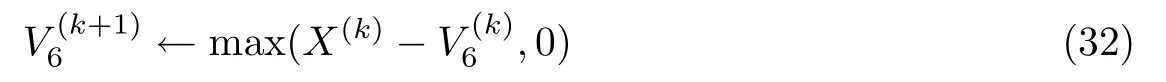
在本文算法中,每次迭代最耗时的部分是计算V5,即低秩项.该项中对于每个图像块奇异值分解(singular value decomposition, SVD)分解的时间复杂度为O((mp)2(np)2),其中np为窗口的空间维度大小,mp为窗口的光谱维度大小,整个图像共划分为P个局部图像块,每个局部图像块在光谱维度上被划分为t/mp个小图像块,该项的复杂度为O((mp)2(np)2t),其中t为光谱库中光谱曲线的条数,本文算法的总体复杂度为O(P(mp)2(np)2).
3 实验及结果
3.1 模拟数据实验
实验采用2 个模拟数据集和1 个真实的高光谱数据集来测试本文算法,其中2 个模拟数据集在3 种不同信噪比(SNR≡E||AX||22/E||N||22,其中E(.)为均值函数)的噪声环境下进行了实验(信噪比分别取10 dB、15 dB、20 dB).本文算法(HSULWLrP)将与最近流行的解混算法如SUnSAL[12]、CLSUnSAL[13]、SUnSAL-TV[15]和J-LASU[17]进行对比实验.
3.1.1 模拟数据集设置
实验从2007年9月发行的splib06 USGS 光谱库中随机选择240 种不同的地物光谱组成实验光谱库,即A ∈R224×240,这些地物光谱含有224 个波段,光谱覆盖范围为0.4∼2.5 µm.由于光谱特征之间的互相关性较高,为了使解混结果更精确,将两条光谱曲线之间的光谱角度设置成大于4.4◦.
1)模拟数据集1(simulated data set 1, DS1):从光谱库A中随机选择了5 个光谱特征作为端元,生成模拟数据集.DS1 有75×75 个像元,每个像元有224 个波段,该数据生成的是线性混合模型,并且对每个像元施加ANC 与ASC 约束.图1展示了DS1 的图像以及5 个端元的真实丰度图.在模拟图像中,一些像元是纯像元,也有一些像元是由2∼5 个端元混合而成的混合像元,这些像元均匀地分布在方形区域中.该数据集的背景像元由5个相同的端元混合而成,且这5 个像元的丰度系数随机固定为0.114 9, 0.074 1, 0.200 3, 0.205 5, 0.405 1.生成DS1 后,采用3 个不同信噪比的噪声(10 dB, 15 dB, 20 dB)对数据集进行高斯噪声污染.
2)模拟数据集2(simulated data set 2, DS2):考虑到大部分场景下不存在纯像元这一条件,DS2有58×58个像元,224 个波段;场景中不包含纯像元,丰度系数满足ANC 和ASC 约束,并且是分段平滑的.与DS1 一样,从光谱库A中随机选择了5 个光谱特征作为端元.图2展示了9 个端元的真实丰度图,并对其添加与DS1 相同强度的高斯噪声.
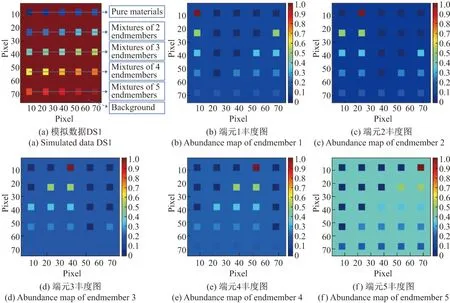
图1 DS1 模拟数据集中的丰度图Figure 1 Abundance maps of the simulated data set DS1
3.1.2 参数设置与评价指标
将每种算法的相关参数调整至最优.表1展示了本文方法与其他对比算法使用的参数.
为了定量地对算法进行评价,实验采用了信号重构误差(signal reconstruction error,SRE)[10]和均方根误差(root mean square error, RMSE)[11]两个量化指标.SRE 表示重建的丰度矩阵与误差之间的比率,SRE 的值越高,说明解混的效果越好.令X为真实的丰度矩阵,为估计的丰度矩阵,则SRE可定义为

RMSE 表示真实的丰度矩阵与估计的丰度矩阵之间的均方根误差,RMSE 的值越低,说明估计的丰度矩阵越准确.RMSE 可以定义为

式中,xij和分别表示真实的丰度矩阵和估计的丰度矩阵中的元素.

表1 对比算法的最优参数设置Table 1 Optimal parameters setting of the comparison algorithms
3.1.3 实验结果与分析
为了验证本文算法的有效性,本节将4 种流行的解混算法与本文方法进行对比,且以SRE 和RMSE 的值来定量地比较5 种方法的解混精度,同时给出了解混得到的丰度图,便于直观地进行对比.
图3展示了在DS1 数据集SNR=20 dB 情况下SRE 关于参数λ、λTV和λLR的函数图.模型共有3 个参数,分别考虑λ和λTV、λ和λLR、λTV和λLR对SRE 的影响.从图3中可以看出参数值对解混结果影响较大,且参数值越小,SRE 值越高,意味着解混结果越精确.
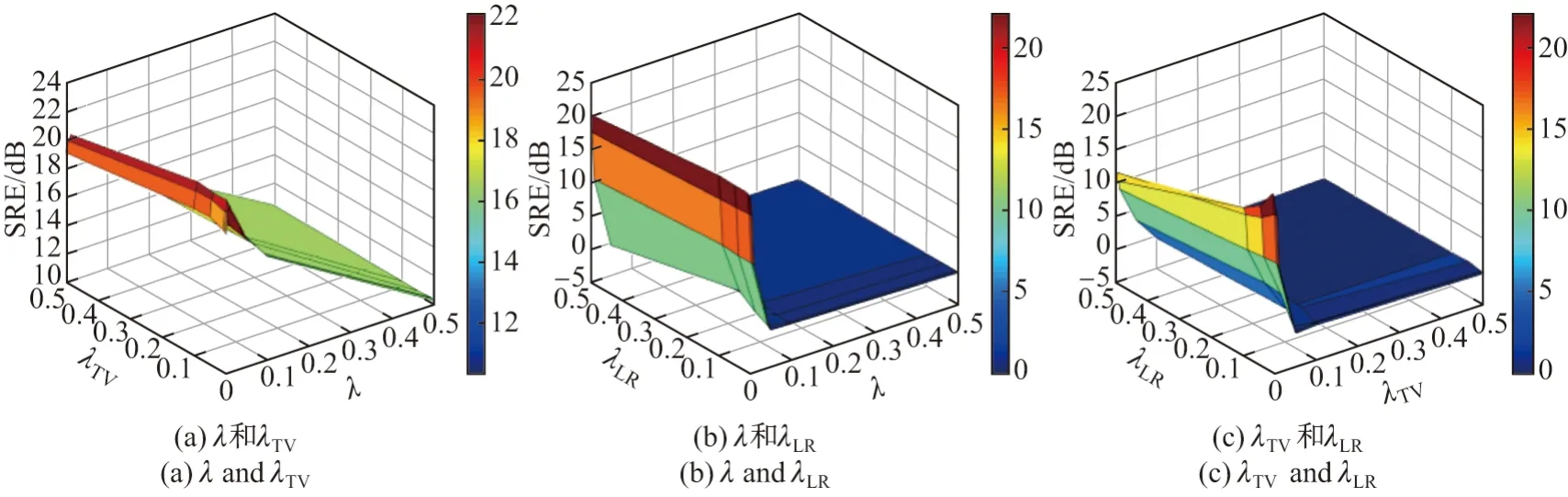
图3 在DS1数据集SNR=20 dB 情况下本文方法中的SRE与参数λ, λT V 和λLR的关系Figure 3 In the case of SNR=20 dB in DS1 data set, the relationship diagram between SRE value and the values of λ, λTV, λLR in the proposed method
图4和5 展示了5 种算法在信噪比为20 dB 的情况下解混得到的丰度图,这里随机给出了一个端元的丰度图.可以看到SUnSAL 和CLSUnSAL 对噪声的抑制效果很差,而施加了TV 项的几种算法对噪声的抑制效果都比较好,然而SUnSAL-TV 仅考虑了TV 项在一些区域造成的过平滑,本文方法不但对噪声的抑制效果很好,而且相比其他算法更好地保留了局部区域的细节信息,避免了仅使用TV 项造成的过平滑现象,所得解混结果也最接近真实的丰度图.表2和3 分别给出了5 种算法的SRE 和RMSE 值,可以看出本文方法的解混结果最好.
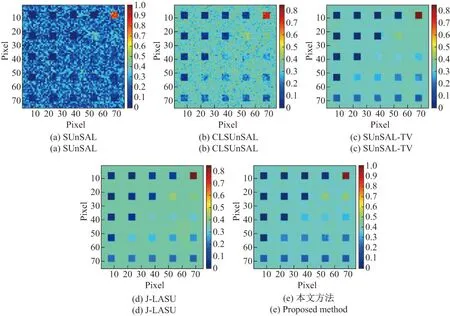
图4 5 种解混算法在SNR=20 dB 时对DS1 中端元5 的解混结果Figure 4 Unmixng results of endmember 5 by the five algorithms with SNR=20 dB in DS1

图5 5 种解混算法在SNR=20 dB 时对DS2 中端元9 的解混结果Figure 5 Unmixng results of endmember 9 by the five algorithms with SNR=20 dB in DS2
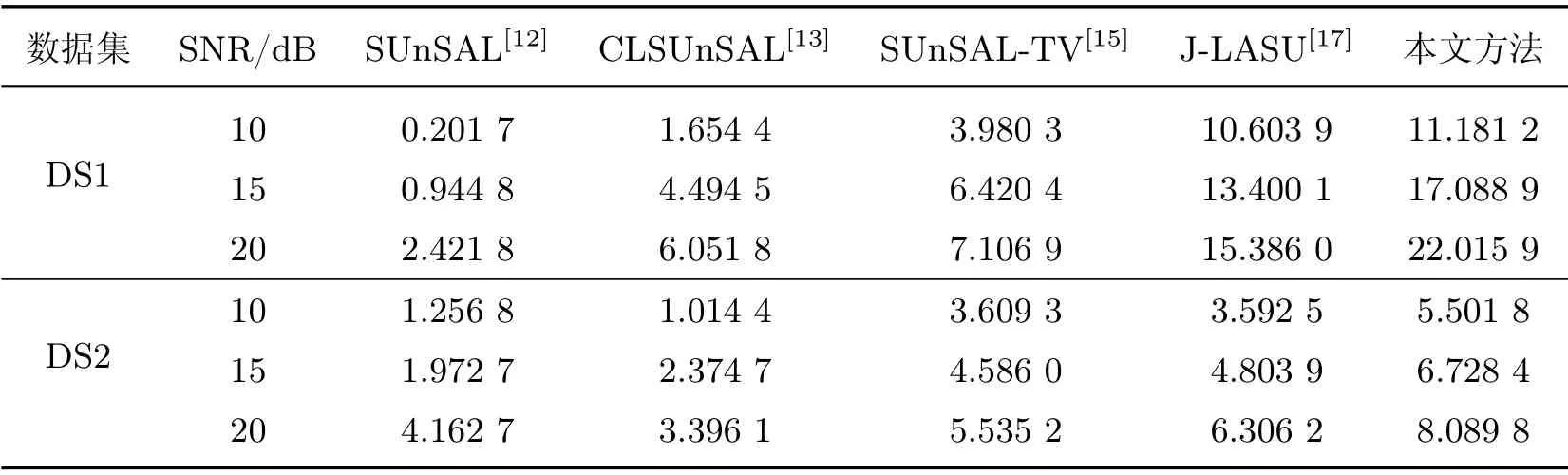
表2 各算法在模拟数据集上的SRE 结果Table 2 SRE results of the algorithms in simulated data dB

表3 各算法在模拟数据集上的RMSE 结果Table 3 RMSE results of the algorithms in the simulated data
3.2 真实的高光谱数据实验
本节利用著名的AVIRIS Cuprite 矿区的数据集来进行真实的高光谱数据实验.该数据集包含了224 个光谱波段,范围在0.4∼2.5 µm,AVIRIS Cuprite 矿区的高光谱图像包含250×191个像元,去除了噪声影响非常大和水吸收影响的波段1、2、105∼115、150∼170、223、224,剩余188 个波段,所采用的光谱库仍然是USGS 的光谱库.图6为5 种算法解混得到的丰度图,从左到右分别是明矾石(alunite)、水铵长石(buddingtonite)、玉髓(chalcedony)3种矿物的解混结果,第1 行是3 种矿物实际的丰度图,需要注意的是实际的丰度图是由Tricorder 3.3 软件于1995年生成的,而实验所使用的公开数据集是在1997年发行的,因此无法进行量化分析,只能作为参照对比,后面几行依次是SUnSAL、CLSUnSAL、SUnSALTV、J-LASU 以及本文方法的解混结果.尽管不能进行量化分析,但从图中可以看出SUn-SAL、CLSUnSAL 对噪声的抑制较差,解混效果并不是很好.SUnSAL-TV、J-LASU 以及本文方法考虑了空间信息,解混结果明显优于前两种算法,但是SUnSAL-TV 在部分区域有过平滑的现象出现,而本文方法对噪声抑制以及局部信息的保留均为最佳,解混结果也更接近于真实丰度图,体现了本文方法的优越性.
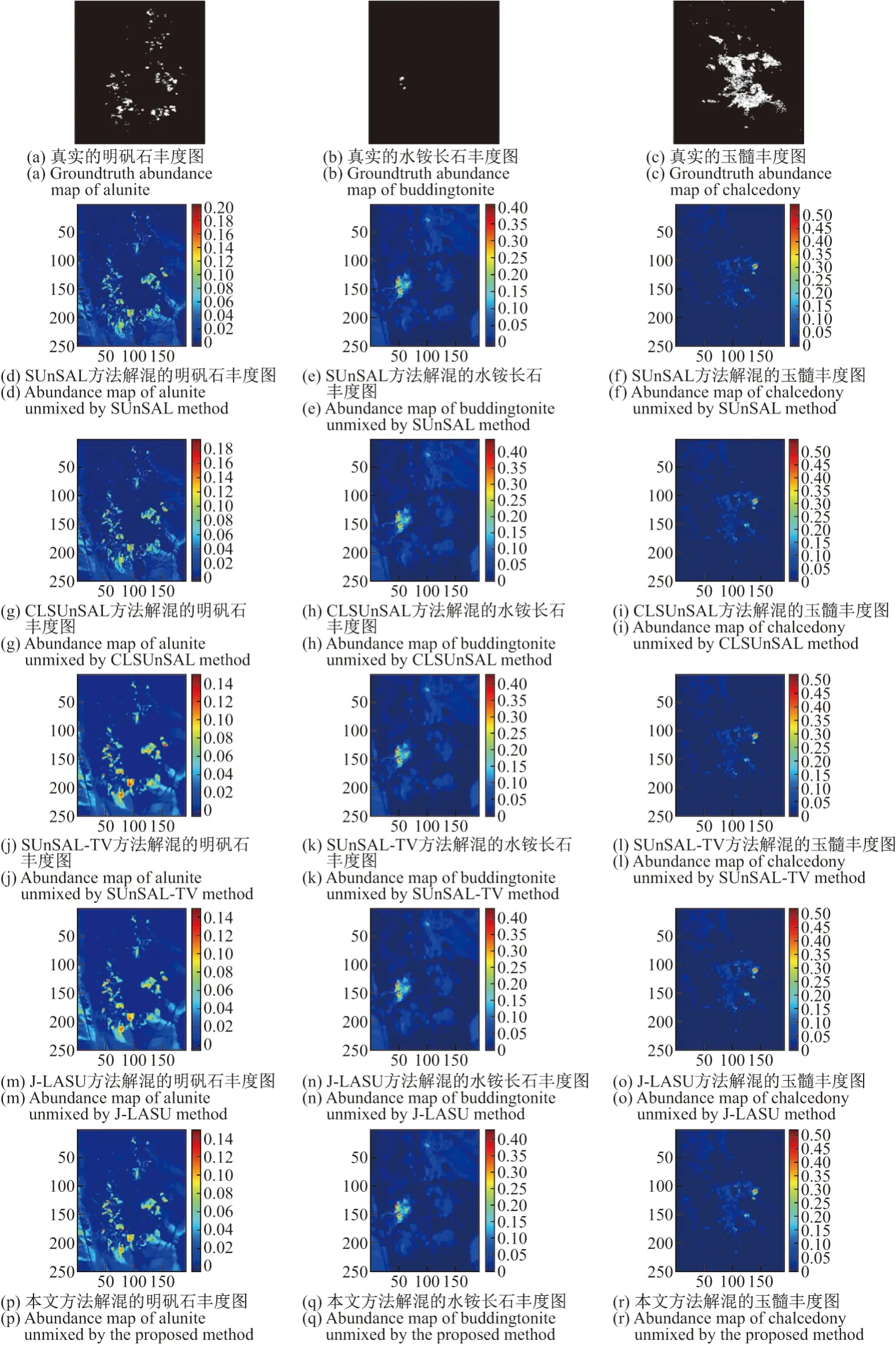
图6 3 类矿物数据真实的丰度图及其由5 种解混方法解混得到的丰度图Figure 6 Groundtruth abundances of three kinds of mineral data and their abundance maps obtained by five unmixing methods
4 结 语
本文提出了一种基于局部加权低秩先验的高光谱稀疏表示解混方法,同时考虑了局部区域的空间信息和光谱信息,在局部区域中相邻的像元包含相同物质的可能性非常高,因此,利用低秩性质可以很好地保留丰度图像的细节信息,同时能够很好地抑制噪声.此外,本文使用了行稀疏对光谱信息进行约束和总变差TV 正则化项来提取空间信息,采用了2 个模拟数据集和1个真实的高光谱数据集进行测试,实验结果显示本文方法优于现有的流行解混算法.

