波浪模式的变分多尺度方法模拟

刘小刚，任睿超，王震，惠小健，章培军

(1.西京学院 理学院，陕西 西安 710123；2.西北大学 数学学院，陕西 西安 710127)

1 引言

波浪模式是流体力学中的一个研究热点[1-5]，水波自由晃动和波浪传播是典型的波浪模式问题，它的性质和规律很大程度上反映了自由面问题的性质和规律，所以对其数值方法进行深入研究具有重大意义。用标准的有限元方法模拟自由面问题时，当对流项或反应项占优时，数值结果会伴随着剧烈的数值伪振荡。这种无任何物理意义的数值伪振荡可以使数值结果严重失真[6]。变分多尺度方法通过对“细”尺度解的近似自动获得稳定化结构的稳定化因子，并把“细”尺度上的近似解代入原偏微分方程对应的Galerkin 变分弱形式以修正“粗”尺度上的解，使得“粗”尺度上的解包含“细”尺度上解的特性，从而提高了数值求解过程的数值稳定性[7-8]，并基于变分多尺度方法，研究波浪模式问题。

2 波浪模式的模型描述

波浪模式的模型方程是一个非定常黏性不可压Navier-Stokes 方程，即

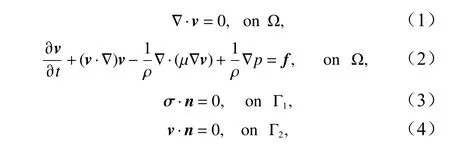
式中，v=(u,v)T为流体的速度向量；p为压力；f=(f1,f2)T为体积力；ρ为密度；μ是运动黏度系数；t为时间；σ为应力张量；Ω为二维求解区域；Γ1为区域 Ω的自由面边界；Γ2为区域 Ω的固壁边界；Γ=Γ1∪Γ2为求解区域的边界；n是边界Γ的单位外法向量。公式中ρ=1 000 kg/m3，μ=1.0×10－2m2/s，重力加速度f2=9.8 m/s2，f1=0.0 m/s2。其中，速度v=(u,v)T、应力张量 σ和法向量n为矢量，其他变量为标量。

3 数值算法

空间离散采用正规网格剖分T={Ωe|,e=1,2,···,nel}，Ω表示计算区域，nel为网格数，h=max{hΩe}，hΩe是网格Ωe的直径。试验函数空间取为

相应的检验函数空间取为

式中，PK(Ωe)是网格 Ωe上的K阶完全多项式。压力空间的试验函数和检验函数空间取为

式（1）和式（2）的变分弱形式为

式中，q是压力的试验函数和检验函数；w、v分别为速度的检验函数和试验函数。

式（2）是一个非线性方程组[9]，对其进行线性化可得

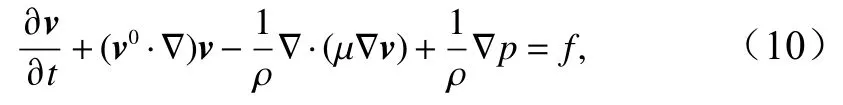
式中，v0为Picard 循环迭代中的前一步数值解。

下面根据变分多尺度的思想建立求解方程（9）的“细”尺度模型。首先把检验函数和试验函数分解到“粗” “细”两种尺度上，即

取如下的空间B={b|b∈(HK/PK)(Ωe),b=0,on∂Ωe;e=1,2,···,nel}，并要求w′(x),v′(x)的每个分量均属于B，即用高阶“泡”近似“细”尺度上的解[10]。

把式（12）代入式（8）可得

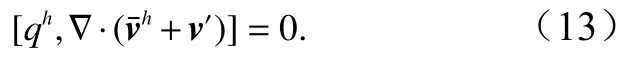
式（12）中的细尺度v′(x,t)可用在时间域上间断、空间域上连续的高阶分段多项式表述。特别地，细尺度v′(x,t)可用时间域上为常数的分段函数表示。因此令于是把式（11）式（12）代入式（9），并分解[10]，可得

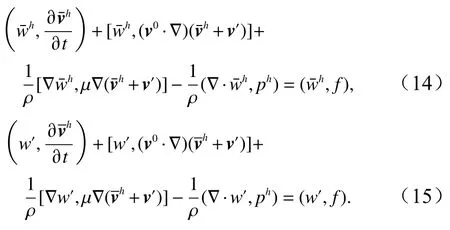
式（14）和式（15）就是动量方程在“粗” “细”两种尺度上满足的控制方程。

下面通过Petrov-Glerkin 方法求解“细”尺度方程（15）。

为简单起见，“细”尺度上的试验函数和检验函数均取一个基函数[10]，分别为则将其代入式（15），由 β的任意性可得“细”尺度上的近似解为

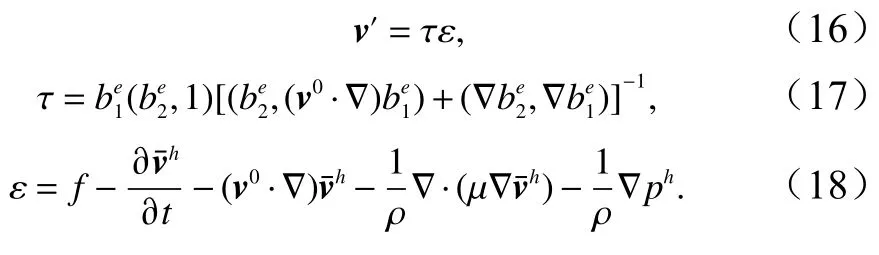
式（16）至式（18）即为基于原偏微分方程残差的“细”尺度上的近似解。

再建立总体变分多尺度方程。把式（16）至式（18）代入式（14）中，由散度定理，可得

将式（16）代入式（13），并运用散度定理，有

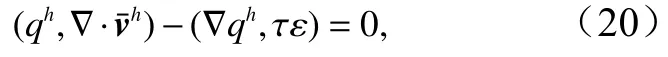
方程（19）和（20）就是要求解的整体变分多尺度方程。

这里采用修正迭代技术确定自由面的位置。自由面上具有如下3 个边界条件：

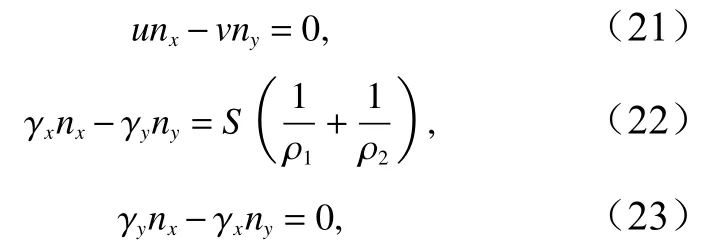
式中，u,v分别为x轴（、y轴）上的速度；nx,ny为垂直于自由面的单位法线，γx,γy是垂直于自由表面力；S为表面张力系数；(ρ1,ρ2)是曲面的主曲率半径。定义h=h(x,t)为t时刻x处的自由面高度函数，则微分形式下的自由面运动条件为

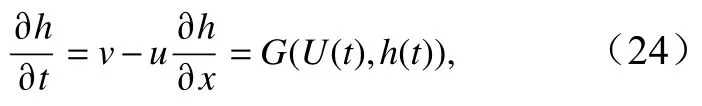
式中，U=(u,v)。选取一阶Euler 格式

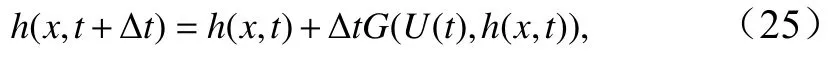
作为自由面运动条件式（24）的更新格式。

4 数值模拟

4.1 水波自由晃荡

计算中采用的时间步长为Δt=0.01，这里计算了一个周期T内自由面的变化趋势，计算区域为1 m×3 m，网格步长为0.1 m，上边界为自由面边界，其他边界为固壁边界，初始波形为η=cos(kx)，从初始波形到恢复初始波形的晃动为1 个周期T。图1 至图5 分别给出了初始时刻和T时刻的速度及压力。

前面在初始时刻指定的初始速度为0，而图1a 和图1b 却给出了非零的速度，这是由于在保持初始自由面位置不变的条件下迭代求解了15 次控制方程，使之达到稳态。

从图2 可以看出，在水体重力的作用下，微幅波左侧水面下降，右侧水面在左侧水体的推动和挤压下上升，并在时刻达到水平状态。由于动力惯性的作用，左侧水面继续下降而右侧水面继续上升，经过约周期的运动后呈现图3 所示的状态。在这一时刻水的速度方向发生改变，开始了新一轮半个周期的运动，如图4 和图5 所示，其分析结果同前所述。由图1至图5 可以看出，水的运动速度呈现周期性变化的规律，压力随着水深的增加而逐渐增大。

4.2 波浪的传播

波浪的传播是海浪模式的一个主要研究内容。图6 至图8 给出了波浪传播的数值模拟结果，其中每个图分别给出了波浪的水平速度、垂直速度和压力。在初始时刻，波浪位于计算区域的中间（图6），随后波浪向左传播。由图7 可见，在波浪向左传播的过程中，波峰向左移动，波峰两边的垂直速度方向相反。图8 显示了波峰传播到左边界的模式。这个算例可以推广到研究海浪与海岸相互作用实际问题中。

5 结论

图1 初始时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.1 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at the initial moment

图2 T/4时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.2 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at the T moment

图3 T/2时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.3 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at the T/2 moment

图4 3T/4时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.4 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at the 3T/4 moment

图5 T时刻波浪的水平速度（ u ）、垂直速度（v）和压力Fig.5 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at the T moment

图6 初始时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.6 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at the initial moment

图7 t=0.8 s 时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.7 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at t=0.8 s moment

图8 t=1.6 s 时刻波浪的水平速度（u）、垂直速度（v）和压力Fig.8 The horizontal velocity (u),the vertical velocity (v),and the pressure of the wave at t=1.6 s moment

变分多尺度方法可以有效地处理具有多尺度效应的数学物理问题。本文在变分多尺度的理论框架内将变分多尺度方法与自由面技术相合，提出了模拟波浪模式的一种新的数值方法，其中自由表面位置的确定由自由面运动条件控制。作为算例，应用此技术数值求解了水波自由晃动问题和波浪传播问题，得到了如下结论：

（1）通过Petrov-Galerkin 方法，用“泡”函数近似“细”尺度上的解，变分多尺度方法可以消除由对流项占优和速度-压力失耦引起的数值伪振荡，并得到满意的数值结果。

（2）对水波自由晃动问题，结合自由面运动条件的变分多尺度方法能很好地模拟自由面的周期性变化趋势，而且速度、压力的分布也呈现周期性变化的规律。

（3）变分多尺度方法能够有效地模拟波浪传播问题，可以进一步推广到研究海浪与海岸相互作用的实际工程问题。