失稳背景流下对称型海洋内波的生成演变

赵艳玲，卢姁，黄泓，刘赛赛，张铭

(1.中国人民解放军31010 部队，北京 100081；2.中国人民解放军32021 部队，北京 100094；3.国防科技大学 气象海洋学院 大气环流与短期气候预测实验室，江苏 南京 211101)

1 引言

海水密度稳定层化海洋中普遍存在海洋内波，其对人类的海洋活动有很大影响。内波对海洋中的混合有重大贡献，其生成机制一直是物理海洋学的重要研究课题之一[1-3]。潮汐与地形相互作用是内波在陆架区的主要生成机制[4-5]。不过，在无潮汐与地形相互作用时，海洋内波也常被观测到[6-7]。Mack 和Hebert[8]通过分析热敏电阻测温资料后，认为剪切背景流的不稳定是赤道东太平洋上层内波产生的主要机制。Lozovatsky[9]在孟加拉南部湾做了观测，揭示了受剪切流不稳定影响的密度跃层中高频内波的基本结构和特征。Zhang 和Alford[10]考察了华盛顿大陆架上非线性内波的不稳定性，在监测到的130 个不稳定内波中，有108 个被确定为剪切不稳定。Yuan 等[11-12]利用内波线性理论模型，分析了黑潮的不稳定性，研究了黑潮附近内波的生成机制。研究指出，对于向西传播的扰动，由南向北的黑潮流场是不稳定的，此时内波从黑潮吸收能量并增长，并提出了黑潮流场不稳定性可激发内波的新观点。他们还用该理论模型解释了卫星SAR 图像观测到的内波与黑潮西边界共存的现象，从而验证了黑潮流场的不稳定性确实可激发出内波。

初始扰动的存在和海洋内波振幅的增长是内波产生的重要条件，而后者与垂向剪切背景流的不稳定性密切有关。对于波动的线性不稳定问题，背景流的失稳与波动的不稳定两者是等价的；可利用标准模方法，将波动的线性不稳定问题转化为一个常微分方程与其边界条件构成的特征值问题，并可离散化为矩阵的特征值问题来数值求解，这也是求解此问题的常用方法[13]；然而对非线性稳定性问题这种方法失效，此时必须采用另外的办法[14]。利用数值实验方法能够研究线性和非线性波动的发展演变问题[15]；故对海洋内波的发展演变，同样可采用数值实验的方法来研究[16-17]。

波动与背景流的配置关系是背景流失稳及波动稳定性问题研究的重要方面。当波动传播方向与背景流方向相同（垂直），即波动的波阵面与背景流方向垂直（平行）时，则该波动称为横波（对称）型波动[13,18]。有关在失稳垂向剪切流下线性和非线性海洋内波生成发展的理论研究及数值实验有不少[16-17,19-20]。然而对于对称型海洋内波的理论研究不多[21]，这方面的数值实验至今也尚未见到。因此，对垂向失稳剪切流下对称型海洋内波的振幅增长形态、波动结构和传播特征、跃层附近波动的表现图像、波动增长的最优尺度，以及线性与非线性波动表现异同等重要问题均需研究和回答。为此，本文利用一个自研的非静力数值模式，对失稳垂向剪切背景流下线性和非线性对称型海洋内波的生成演变做了数值实验，试图回答以上重要问题，并进行讨论。

2 数值模式和实验方案

采用无海底地形的二维非静力准不可压缩方程组，考虑了海洋跃层和剪切背景流的作用，并设扰动（内波）传播方向为x方向，水平背景流的流向垂直于该扰动的传播方向，即该流向为y方向；再设该扰动（内波）沿背景流的流向是均匀的，也即对该扰动（内波）有∂()/∂y=0，而y方向也是该扰动（内波）波阵面的方向。z方向由海底垂直指向海面，并设海底为z=0。这样依据文献[22-23]，并取对称型扰动形式后，该数值模式所使用的控制方程组为

式中，ζ=∂w′/∂x－∂u′/∂z为等y面上的涡度，且满足泊松方程ζ=∇2ψ，ψ为流函数；u′、v′、w′分别为x、y、z方向的扰动流场；σ′=－gρ′/ρ0，σ′为位密度扰动，ρ′为密度扰动，在此 ρ0为海水标准密度，取为常数；N2=N2(z)为海洋层结参数；f为地转参数；g为重力加速度，对海洋内波均取为常数。在式（1）中，非线性项为u′∂()/∂x（平流项）和w′∂()/∂z（对流项），若略去这两项就成为线性模式，否则为非线性模式。因不考虑海底地形以及本模式海面采用刚盖近似，故上、下边界条件为

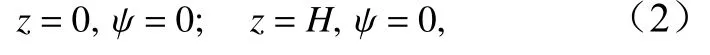
在数值求解该控制方程和边界条件时，首先对该方程做数值积分，得到下一时刻的ζ、v′、σ′值；然后用超松弛迭代法解泊松方程ζ=∇2ψ得到 ψ；再由u′=－∂ψ/∂z，w′=∂ψ/∂x通过差分求得u′、w′，由此得到该时刻的所有变量值；之后再对该方程继续进行数值积分，如此循环往复，直至积分至指定的时刻终止。模式水平范围为48 km，水平方向取601 个格点，格距为80 m；垂直范围（海深）取1 840 m，分23 层，有24 个层次，第1 层次为海底（下边界），第24 层次为海表面（上边界），层次间距也为80 m。水平侧边界取海绵边界条件。空间差分取中心差，时间积分取前差迭代方案，积分时间步长取12 s。

模式在第22 层次有跃层存在，在该层次取层结参数N2=10－4s－2，而其他层次均取N2=10－8s－2。之所以这样取是因实际海洋中除跃层外，其他地方密度垂向变化都很小。因实际海洋中往往存在跃层以下流动与表层相反的情况，故本文中取该模式的背景流为：在海底为-0.5 m/s，之上至海表面呈线性变化，海表面其值取0.5 m/s。模式中取地转参数f=0.694 0×10－4s－1（28.5°N 处的值）。

本文用流函数来表示流场扰动，在其正、负中心的外围分别有顺、逆时针旋转的环流圈，扰动速度的大小则由流函数等值线的疏密程度来反映。在下文流函数与位密度分布图中，横坐标为x方向（指向右方），x值为距左边界（x=0处）的距离，单位为80 m，此值也可视为x方向的水平格点数（以下简称格点），左、右边界的格点分别为0、600；纵坐标为z方向（指向天顶），其值为垂向层次数；y方向则由页面之外垂直穿透页面。这些以下都不再赘述。本文数值实验中模式的积分终止时刻：线性情况为30 h，非线性情况为72 h。

模式初始无流场扰动。初始位密度扰动场在垂直和水平方向分别呈半个简谐波形态，垂直和水平半波长分别为1 840 m（海深）和320 m（4 个格距），其中心在距左边界20.08 km（格点251）的海深一半（水深920 m）处；半个简谐波范围在格点249～253 间的各层次之内，而之外，初始位密度扰动的值都为0；该范围中心处的位密度扰动值，也是最大值（振幅）为10－3m/s2。

以上数值实验中所用的背景流、层结等环境参数以及初始场均取理想而非实际值，但大多符合实际海洋的典型情况[17]。

3 线性模式内波生成发展

3.1 速度场演变

现利用上述线性模式来分析剪切背景流的失稳和内波的发展过程。本文取是格点总数）来反映全场扰动速度随时间的变化，并用以分析波动的发展演变过程，在此表示对该模式范围的所有格点求和。因本文初始场仅有位密度场扰动而无流场扰动，故开始积分后，流场和位密度场会相互调整，激发出重力惯性波，并向周围传播。

图1a 给出了E值随积分时间的变化。由图1 可见，在积分的前12 h，E值大致呈指数形式很缓慢地增加，12 h 后E值则呈指数形式急剧增大，这表明该系统进入迅速发展阶段，也即该系统明显存在不稳定，对线性模式，背景流的失稳与扰动的不稳定是等价的；因在此层结是稳定的，故从该扰动系统与背景流的配置来看，该不稳定属对称不稳定，其是重力惯性内波的不稳定。

南宋时期，东西部文化差异及差距客观存在，而陆游以东部吴越文化的视角考量西部，将一些差异也变成差距，无疑加深了其差距的尺度，增加了地理学的人文情感因素。

3.2 流函数

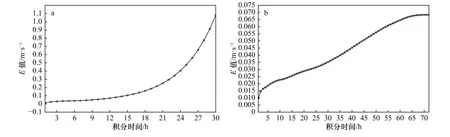
图1 线性(a)和非线性(b)模式中E 值随时间变化Fig.1 The variation of E values over time in linear (a) and nonlinear (b) models

图2 给出了流函数的空间分布。积分3 h（图2a）可见，在初始位密度周边，原先静止的流场现已出现了两个流动方向相反的环流圈，两环流圈之间有几乎垂直的较强上升流，而其他各处流动微弱。积分6 h（图2b），该两个环流圈由原来的一个中心现演变为在其上、下部各有中心，且上部中心在左，下部中心在右，环流的强度也在增加，此时模式范围内扰动速度场u′的最大值为0.61 m/s。积分12 h（图2c），以上两个环流圈又演变成倾斜环流系统，该系统由具有正、负中心的两个倾斜环流圈组成，在系统正、负中心之间从海底向上至跃层之下有强倾斜上升流，且该系统已演变成经典的对称不稳定环流系统[22]，此时为0.80 m/s。积分18 h（图2d），该对称不稳定环流系统强度持续增加，形态变化不大，仅在其左、右两侧有新的倾斜扰动出现，此时为1.33 m/s。积分24 h（图2e），该系统强度继续迅速增加，但形态仍变化不大，在其左、右两侧的倾斜扰动持续发展，此时为3.45 m/s。积分30 h（图2f），该系统形态仍维持，强度还在迅速增强中，此时增至8.91 m/s，已高出海洋典型流场10 cm/s 约2 个数量级，为此结束该数值实验。

由图2 可见，积分12 h 后流函数的主体形态即正、负倾斜环流圈的水平尺度维持大体不变，此时该主体形态的水平尺度约为6.4 km，其远大于初始扰动尺度320 m；这表明该尺度是在本文所取环境场（即地转参数，层结参数和背景流，其与典型值相差不远）下，线性对称不稳定的最优增长水平尺度。从该主体形态的位置看，在扰动发展中其位置不变，这表明线性对称不稳定是原地增长的。

3.3 位密度

图2 线性模型中流函数的空间分布（等值线表示流函数，单位：m2/s）Fig.2 The distribution of stream functions in linear models (isolines represent stream functions,unit:m2/s)

因位密度扰动 σ′与密度扰动 ρ′成正比，比例系数－g/ρ0为常数，故可分析 σ′的演变来得知 ρ′的演变。图3给出了各时刻 σ′的空间分布，初始时其空间分布如上文所述。积分3 h（图3a）可见，σ′的分布与初始时截然不同，其扰动中心已由海深一半处垂向移至初始扰动上方的跃层（22 层）及之上，并向左右传播。积分6 h（图3b），σ′这种态势分布大体维持，并出现了从左至右的负、正、负的3 个扰动中心，扰动强度也有所增强。积分12 h（图3c），跃层及附近 σ′分布的态势仍基本维持，其强度还在增加，此时原先3 个扰动中心，现在最右边的消失，成为一对扰动中心，并与之相应在海底附近也开始出现扰动中心。积分18 h（图3d）跃层及附近 σ′的分布态势依然维持，强度进一步增加，原在海底附近的扰动中心加强并向斜上方伸展，构成倾斜方向贯穿整个水体的正扰动带。积分24 h（图3e），σ′的分布大体态势不变，仅强度进一步不断增强。积分30 h（图3f），σ′的分布态势仍大体不变，但强度迅速加强，此时在原先倾斜贯穿水体的正扰动带两侧又出现了贯穿水体的负扰动带，该正扰动带与从海底向上至跃层之下的倾斜强上升流相配合，而负扰动带则与该强上升流两侧的倾斜下沉流相配合。

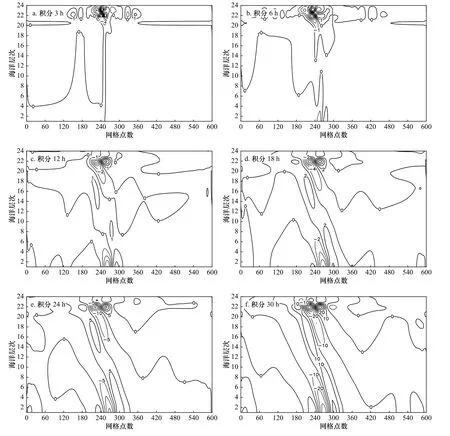
图3 线性模型中位密度扰动场的空间分布（等值线表示位密度，单位：10-4 m/s2）Fig.3 The distribution of potential density perturbation in linear models (isolines represent potential density,unit:10-4 m/s2)

综上，线性对称不稳定12 h 后位密度扰动 σ′的大值中心位于初始扰动水平位置上方的跃层附近，以后位密度扰动 σ′的分布形态也大致不变，仅强度增加。这表明海洋内波被跃层所俘获，并与实际海洋内波的观测相一致。与流函数相应，位密度扰动也呈原地增长，其最优增长水平尺度同流函数。

4 非线性模式内波生成演变

本节分析非线性模式中内波的生成演变规律。该模式中因存在扰动与扰动的相互作用，故背景流的失稳与扰动的不稳定并不等价，这与线性模式不同。这里非线性模式中的环境条件（背景流和层结参数等）以及初始场均取得与线性模式相同。

4.1 速度场演变

在此与线性模式相同，也用E值随时间的变化来反映波动的发展演变过程。由图1b 可见，扰动在开始的6 h 内E值变化较激烈，以后E值大体按线性形式增长，这与线性的情况有很大不同，到65 h 后，增长几乎停止甚至出现衰减。将图1b 与图1a 相比较可见，在积分30 h 前，非线性的内波增长要较线性慢，且12 h 后其增长仍呈准线性形式，这与线性的指数增长不同，并由此可见非线性效应有维稳作用。

4.2 流函数

图4 给出了流函数的空间分布。由积分3 h（图4a）可见，此时其流函数分布与线性情况大体相同，不再赘述。积分6 h（图4b），此时流函数的分布已与线性情况有所不同，在海洋中层原初始扰动场位置及两侧出现了4 个从左至右的负、正、负、正的环流中心，及与这些中心相对应的垂向环流圈，此时模式范围内扰动速度场u′的最大值为0.17 m/s。积分12 h（图4c），以上4 个环流圈中原先左边第3 个环流圈发生了倾斜，在该环流右下方的海底之上出现了垂向等值线的密集带，表明该处垂直运动强，此时仍为0.17 m/s。积分24 h（图4d），原先倾斜环流圈左、右两侧的环流圈也发生倾斜，原先的垂向等值线密集带现已消失，不过在格点210 附近的海底之上又出现了新的垂向等值线密集带，表明此处垂直运动很强，此时仍维持在0.17 m/s。积分36 h（图4e），在原先较强的负环流圈的左、右两侧又形成了较强的负环流圈，这表明负环流圈在总体增强，而垂向等值线密集带的位置则基本不变，此时增加到0.20 m/s。积分48 h（图4f），负环流圈总体增强的趋势仍维持，左侧的负环流圈强度增至最大，右侧的强度也明显增加，不过中间的负环流圈强度减弱，3 个负环流圈的倾斜度都略有增加，而原先垂向等值线密集带则略有右移，此时为0.19 m/s。积分60 h（图4g），原先最左边正环流圈左侧很弱的负环流现明显增强，在模式范围水体内现有4 个负环流圈，原先垂向等值线密集带的位置仍略有右移，不过在该密集带左边的海底之上又新生了垂向等值线密集带，这表明扰动向左、右跳跃式传播，此时则为0.22 m/s。积分72 h（图4h），流函数分布态势变化不太大，扰动仍向左、右方传播，并已覆盖至模式的全部范围，两条垂向等值线密集带的位置仍都略有右移，此时为0.19 m/s。

综上，在此流函数的发展演变与线性情况不同，流函数向左、右方的传播明显，流函数环流圈的正、负振幅也不对称，负振幅要更大，并在海底之上会生成流函数垂向等值线密集带，其可看成间断；然而流函数的倾斜环流圈以跃层为顶盖这一点，则对线性和非线性情况都适用。

4.3 位密度

图5 给出了各时刻位密度扰动 σ′的空间分布，初始的空间分布见上文。由积分3 h（图5a）可见，σ′的分布与线性情况也大体相同，不再赘述。积分6 h（图5b），与线性情况相比，在跃层及之上的 σ′扰动向左、右方传播较快，并出现多个正、负扰动中心。积分12 h（图5c），在初始扰动中心之上的跃层及附近，σ′出现了一个负中心，其左、右侧各有一个正中心，左侧的正中心倾斜向下伸展，在跃层之下又形成一个较强的正中心；与跃层上负中心的水平位置相应，在海底也有一个负中心向上伸展，在其左侧海底之上出现了位密度垂向等值线的密集带，表明该处位密度水平梯度很大。积分24 h（图5d），σ′分布的变化不很大，原海底的负中心明显加强，与跃层之下海洋上部的正中心形成正、负中心倾斜对峙的形态，在海底该负中心的左侧又出现一个较弱的正中心，在该较弱正中心左侧海底之上新生了一条位密度垂向等值线密集带，而原先的那条消失。积分36 h（图5e），σ′分布的变化仍不太大，原先在海底的负中心明显加强，原先新生的垂向密集带现在其位密度水平梯度还在加剧。积分48 h（图5f），在原先 σ′正、负中心倾斜对峙位置的左、右方分别又出现了同样的倾斜对峙形态，这样就总共有3 个该对峙形态，原先的垂向密集带略有右移。积分60 h（图5g），原先3 个对峙形态的负扰动中心均增强，正扰动中心均减弱，在原先左边对峙形态的左侧又新生成一个对峙形态；原先的垂向密集带仍略有右移，在其左边又新生了一条垂向密集带。积分72 h（图5h），扰动继续向左、右方传播，最右边又新增加了一个对峙形态，现对峙形态已增加到5 个，并总体上保持负中心强，正中心弱的态势，原先的两条垂向密集带依然略有右移，但右边的那条水平梯度有所减弱，此时位密度扰动 σ′已覆盖该模式的全部范围。

综上，非线性情况当存在跃层时，海洋内波同样会被跃层所俘获，在跃层上始终也都存在位密度扰动的大值中心，并最终形成多个正、负中心倾斜对峙的形态；每个对峙形态中位密度扰动的正、负中心分别对应于流函数环流圈上的倾斜上升、下沉流；非线性效应也会造成位密度等值线的密集，形成垂向密集带，其也可看成间断。

5 讨论

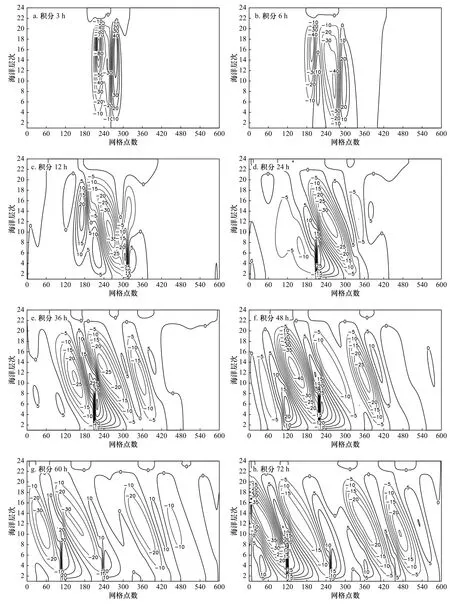
图4 非线性模型中流函数的空间分布（等值线表示流函数，单位：m2/s）Fig.4 The distribution of streamfunctions in nonlinear models (isolines represent stream function,unit:m2/s)

图5 非线性模型中位密度场的空间分布（等值线表示位密度，单位10-4 m/s2）Fig.5 The distribution of potential density perturbation fields in nonlinear models (isolines represent potential density,unit:10-4 m/s2)

首先，比较本文取同一失稳垂向剪切背景流下，线性与非线性对称型内波的差异。线性内波强度呈指数增长态势，该内波是对称不稳定的。而非线性内波的强度有很长一段时间大体呈线性增长，可看作该内波的发展期，此时的增长要比线性的指数增长小很多，以后该内波进入稳定期，不再增长甚至略有衰减（图1）。这表明非线性效应抑制了内波增长，最终使扰动趋于稳定，非线性效应具有维稳作用。之所以这样是因为在非线性模式中，除了存在线性模式中的背景流与波动的作用，背景流将能量输送给波动，使之发展（不稳定）之外，还存在因非线性项（平流项和对流项）引起的波波相互作用；该作用使某个从背景流获得能量而发展的波又会将能量转移到其他波上，从而因能量的流失而抑制了自身的发展；该非线性过程十分复杂，难以解析求解。文献[14]曾讨论了正压大气的非线性不稳定问题，然而本文所用的控制方程组是非静力的，远较正压大气的复杂，故对本文控制方程组的非线性稳定性至今尚无理论证明，这也是本文要进行数值研究的原因。对线性内波的对称不稳定，随着积分时间增加，扰动波形基本不变，正振幅和负振幅两者大体相同，且呈符号相反原地增长的倾斜环流圈，在该环流圈之间则有强倾斜上升流，理论分析的情况也是如此[21,24]。非线性内波情况有所不同，因非线性项的平流和对流作用，其波形随积分时间的增加而发生变化，倾斜环流圈数目也在增加，并最终形成负环流强度大于正环流强度的结果，即非线性内波的负振幅要大过正振幅[25]。由于非线性追赶效应（主要由平流项造成），随着积分时间增加，会导致流函数及位密度扰动水平梯度越来越大，形成等值线密集带，并可视为间断[25]，而线性情况因无平流项不会出现此情况。

其次，讨论该对称型不稳定波动的性质。由上可知，无论是线性还是非线性内波，都有正、负位密度扰动区对应于上升、下沉运动区。注意到位密度扰动与密度扰动正、负符号相反，这样就有负密度扰动区对应于上升运动，正密度扰动区对应于下沉运动，故而此种运动属于对流；然而这时层结是稳定的，这样就不可能有纯垂直对流的发生，此时只有倾斜对流才能得到维持和发展。大气中对称不稳定也称之为斜对流不稳定，并可用等熵面（等位温面）上的微团运动来讨论[24]，对海洋而言，等位密度面则起到了等位温面的作用。

最终，要讨论实际海洋中是否存在内波对称不稳定的问题。黑潮是一支强西边界流，其在跃层之下的流向与跃层上的流向相反，表现为一支垂向剪切流。引言中已提到Yuan 等[11-12]指出，对于向西传播的扰动，由南向北的黑潮流场是不稳定的，并解释了观测到的内波与黑潮西边界共存的现象。由于黑潮自南向北流，而扰动向西传播，显然扰动（内波）的传播方向与背景流（黑潮）垂直，而观测到的内波与黑潮西边界共存则表明该内波波阵面平行于背景流（黑潮），故该内波为对称型内波；因背景流（黑潮）的失稳，致使该内波得以生成和发展。如此看来，在实际海洋中垂向剪切流的失稳造成对称型内波的生成发展应该确实存在，并值得进一步研究。

6 结语

本文采用无海底地形但考虑海洋跃层和背景流的二维非静力准不可压缩方程组，以及据此自研的数值模式，对失稳垂向剪切背景流下线性及非线性对称型海洋内波的生成发展做了数值实验，所得主要结论有：

（1）失稳垂向剪切背景流下，对称型内波得以生成发展，线性情况则有内波的对称不稳定，该内波强度呈指数增长；非线性情况内波强度在发展期呈准线性增长，最终进入稳定期；线性增长比非线性增长要快得多，而非线性效应具有维稳作用。

（2）对该生成发展的线性、非线性对称型内波，在跃层处的位密度扰动均存在大值中心，即其为跃层所俘获，这与实际观测相一致；流函数与位密度扰动有很好匹配，位密度扰动的正、负中心分别相应于流函数的上升、下沉运动，这表明有斜对流发生，且该斜对流以跃层为顶盖。

（3）随积分时间增加，该线性对称型内波的波形大体不变，正、负振幅也大体相同，且呈现符号相反原地增长的两个倾斜环流圈，在它们之间有强倾斜上升流；而非线性对称型内波的波形则随积分时间改变，倾斜环流圈数目也在增加，最终形成负环流强于正环流的态势，并有流函数、位密度扰动的水平梯度剧增，其可视为间断。

最后要指出的是，关于实际海洋背景流、环境参数和初始场的数值实验，则是我们今后进一步要开展的工作。