海底峡谷内浊流流动与沉积特征数值模拟研究

王越，孙永福,2*，修宗祥，宋玉鹏，王柯萌，谢秋红

(1.自然资源部第一海洋研究所，山东 青岛 266061；2.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室，山东 青岛 266237；3.中国海洋大学 工程学院，山东 青岛 266100)

1 引言

海底浊流是陆源物质向深海输运的重要营力，形成的浊积岩为重要的油气储层已成为业界共识，现代实测资料证明浊流可由地震、滑坡、高浓度河流入海等因素触发，经大陆架或大陆坡的海底峡谷流入深海，在坡度平缓处形成巨大的海底扇[1-4]。故研究海底峡谷中浊流的流动过程与沉积特征对理解现有沉积结构的沉积过程、反演深海水动力环境及探测海底油气储层具有重要意义。

自1887 年Forel[5]发现浊流以来，Daly[6]、Kuenen[7]、Bell[8]等人逐渐将浊流与海底峡谷成因、深水沉积物输运联系在一起，从理论与实验的角度发表了一系列成果[9]。随着探测手段的发展，相关的研究学者相继在峡谷中观测到浊流活动，并对浊流的触发机制、速度等特征剖面进行了深入研究[10-14]。但由于浊流偶发性强、破坏性大，高速、偶发性浊流的实地观测难以解决[9,14]，水槽实验与数值模拟仍是研究浊流的重要方式。

自Kuenen 和Migliorini[15]开展水槽实验对浊流的流动过程进行了研究，Middleton[16]针对浊流与密度流的自异性展开研究。各国学者相继对坡度、速度、浓度等参数对浊流特征剖面的影响进行了系统性的研究[3,17-19]，推动了浊流理论的长足发展。但因水槽实验的尺度限制，浊流的数值模拟研究迅速进入到蓬勃发展时期。Britter 和Simpson[19]研究了浊流在斜坡上的流动过程，并探讨了坡度、沉积物交换与流体夹带对浊流流动的影响。Huang 等[20-25]、Kassem 和Imran[26]、Strauss 和Glinsky[27]、Serchi 等[28]学者相继对浊流的数值模型、溢流现象、侵蚀性进行了数值模拟研究，极大丰富了现有的浊流理论。姜涛等[29-30]和Jiang 等[31]基于FLUENT 对浊流形成的水动力条件以及浊流机制的沉积物波进行了模拟。Georgoulas 等[32]构建三维数值模型，对比前人实验，验证浊流三维模拟的可行性，并分析了浊流对海底的冲击作用。郭彦英和黄河清[33]模拟了不同坡度下浊流的流动与沉积过程，发现坡度对浊流的沉积位置起关键性作用。

由上述相关的研究概述可知，海底浊流及其沉积的数值模拟多为斜坡-平滑水平坡的研究。但实际海底峡谷地形复杂，单坡折带无法展现浊流在复杂地形下的流动与沉积情况。故研究浊流在陆坡峡谷-大陆架沉积扇-平缓斜坡等连续坡折地形下的流动与沉积特征，对预测浊流沉积特征，反演浊流沉积环境及探测海底油气储层具有重要意义与参考价值。本文借助CFD 软件FLUENT，基于双欧拉（Euler-Euler）多相流与湍流k-ε 模型，求解不可压缩流体Navier-Stokes（RANS）方程，对浊流在二维连续坡折地形下的流动与沉积过程进行了数值模拟，探讨浊流在连续坡折地形下的流动特征与动力地貌过程。

2 数值计算模型概述

2.1 控制方程

浊流属沉积物重力流的一种，由悬浮沉积物引起的密度差异所驱动[34]。本文将悬浮颗粒物设为固相，为保证初始条件不受太大限制，采用双欧拉多相流法对浊流进行数值模拟[31-32]。

2.1.1 体积分数方程

Euler-Euler 两相流中，两相看做可相互穿插的连续流体，体积不可互相占据，故模型构建时引入体积分数的概念。体积分数视为时间与空间的连续函数，不同相体积分数之和为1，每相的体积分数可表达为

式中，aq是q相的体积分数。故q相有效密度为

式中，ρq是q相的密度。

2.1.2 质量方程

每相的连续性方程，通过经验方程或运动学方程而封闭[29]，基于体积分数的概念，浊流的连续性方程由下式给出：

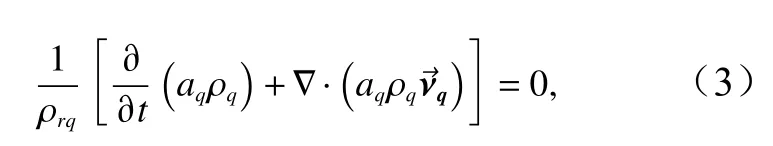
式中，ρrq是q体积平均密度；为q相速度。

2.1.3 动量方程

本文采用基于固-液两相流的双欧拉方法对浊流进行模拟，其动量方程由以下方程给出：

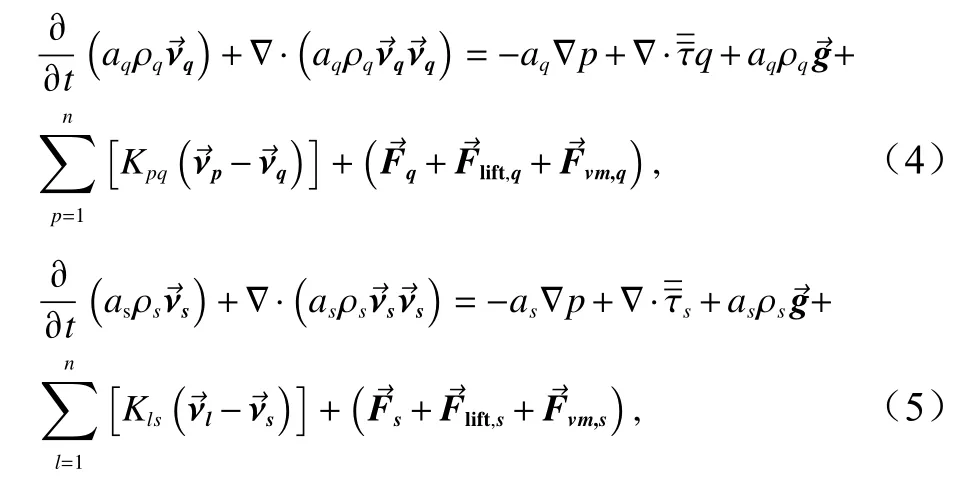
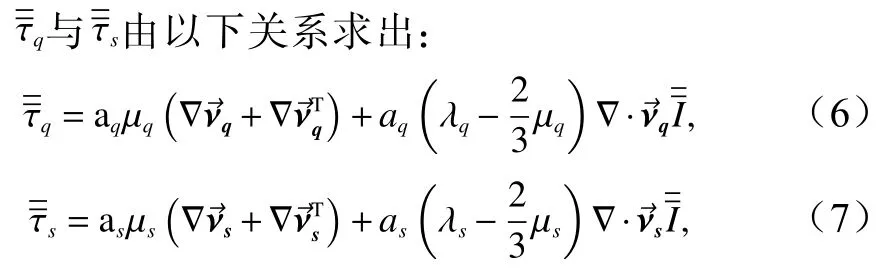
2.2 模型建立

考虑大陆坡的平均坡度在4°～5°之间，同时为方便与前人水槽实验数据比对，本文建立了长5 m，坡度为4.6°的斜坡连接6.5 m 水平坡，水平坡接2°缓斜坡的几何模型模拟浊流在陆坡峡谷-大陆架沉积扇-平缓斜坡地形上的流动与沉积过程（图1）。入流口设定0.10 m 水平段以调整入流方向，2°缓斜坡确保浊流在流动过程中不会出现回流的情况。浊流入流高为0.03 m，悬浮颗粒密度为2 650 kg/m3。如图1 所示，为保证计算精度同时节省计算时间，按0.05 m 的网格尺寸对该模型进行网格划分，近壁面区域按0.01 m 的精度进行局部网格加密（图1 中加粗区域），采用有限体积法对网格离散，以计算流体区域的流动情况。

2.3 边界条件

浊流入流流速与悬浮颗粒体积浓度由初始条件给出（表1），湍动能与湍流耗散率则由经验公式推算给出[17]。入口边界为速度入射边界，不考虑两相滑移速度。出口为压力出口，流量全部由流域内流出，为开放型流动边界。自由水面采取对称边界，由于浊流触发水深常在500 m 以下的深海，故该边界对深海浊流的流动几乎没有影响。底部边界为粗糙无滑移的固定边界。

图1 计算网格（加粗区域为近壁面网格）Fig.1 The mathematic grid (the bold area is the near-wall grid)

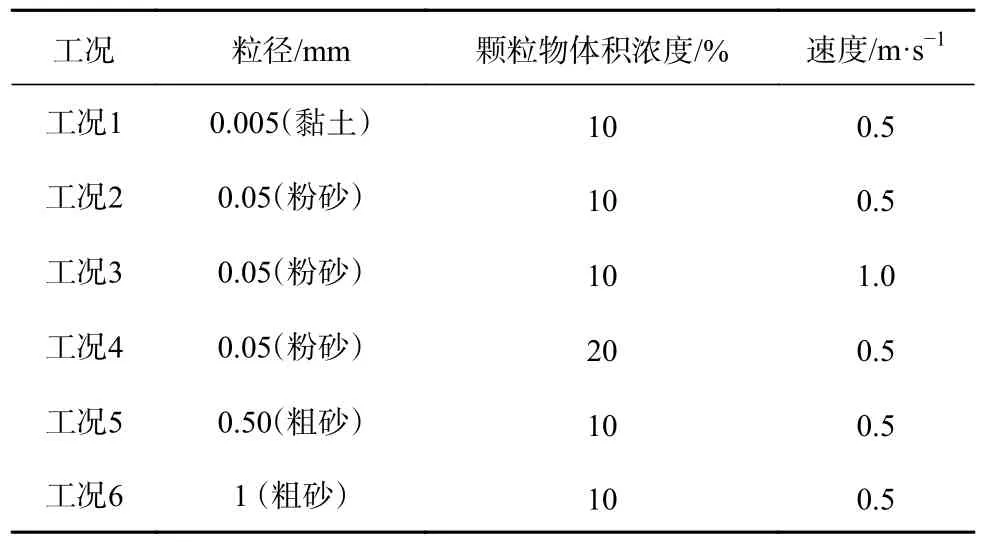
表1 初始入流条件Table 1 Numerical simulation initial conditions

2.4 模型验证

为验证该模型的可行性与可靠性，本文采用Garcia和Parker[3]浊流实验组数据对该模型进行验证。Garcia和Parker[3]所用实验装置如图2 所示，左侧为流体混合装置，保证浊流以均匀浓度注入水槽，右侧供应清水以保持自由水面不变，为实现数值模拟，将主要流动区域简化为斜坡与水平面相连的几何模型。

参照浊流实验组NOVA7 设定相同浓度、速度与颗粒密度等参数，将数值模拟结果与实验结果进行对比研究（图3）。比对得出两点的浊流速度剖面与Garcia和Parker[3]实验情况基本吻合，斜坡下的流速模拟结果与实验吻合较好，坡上数模浊流厚度较厚，可能是由于数模中浊流沿斜坡流下，而实验室则为跌落式排出。

3 模拟结果

3.1 浊流头部特征

浊流可划分为浊流头部与浊流本体两个部分，在流动过程中，浊流头部排开环境流体，引导浊流沿海底流动，其形态与结构受到浓度、速度及悬浮颗粒物粒径等参数的影响。

3.1.1 浊流头部速度分布

驱动浊流流动的悬浮颗粒物粒径与浊流头部结构密切相关，浊流头部的速度分布如图4 所示，黏土等细粒物质驱动的浊流头部较粉砂与粗砂更易发生混合化作用，自由剪切层由于湍流运动产生的不稳定的横向涡旋而形成“云状拖曳”现象更为明显（图4a）。且细粒悬浮物驱动的浊流具有明显的速度核心，层级特征显著。随粒径增大，浊流的头部特征逐渐弱化，层级化逐步模糊至消失。环境水体夹带系数可能与粒径有关，粒径越大系数越小，浊流厚度随之减小，故粗砂驱动的浊流呈现散乱细长的头部特征。

随入流速度增加，浊流头部表现出更强的层级结构（图4b，图4c），自由边界层的悬浮颗粒物由于环境水体的夹带，具有清晰的湍流扩散层。相似的结构特征变化也体现在入流浓度上（图4b，图4d）。

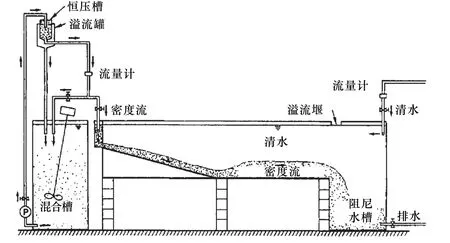
图2 Garcia 和Parker[3]实验装置图Fig.2 The experiment device schematic of Garcia and Parker[3]

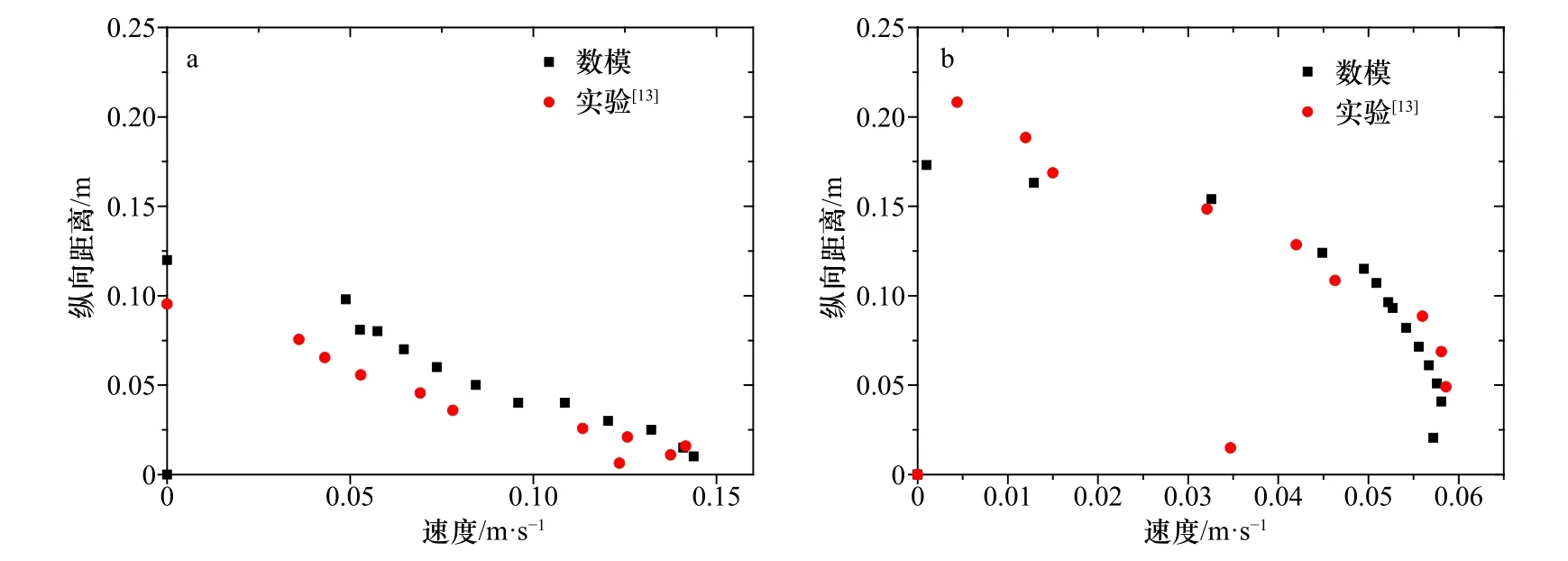
图3 实验中模型3 m 处（a）和8 m 处（b）浊流垂向速度剖面与模拟结果对比（坡折带在模型5 m 处）Fig.3 Comparison the vertical velocity profiles of laboratory and simulation results at the sites 3 m (a) and 8 m (b) from the inlet(the break in slope is at 5 m from the inlet)

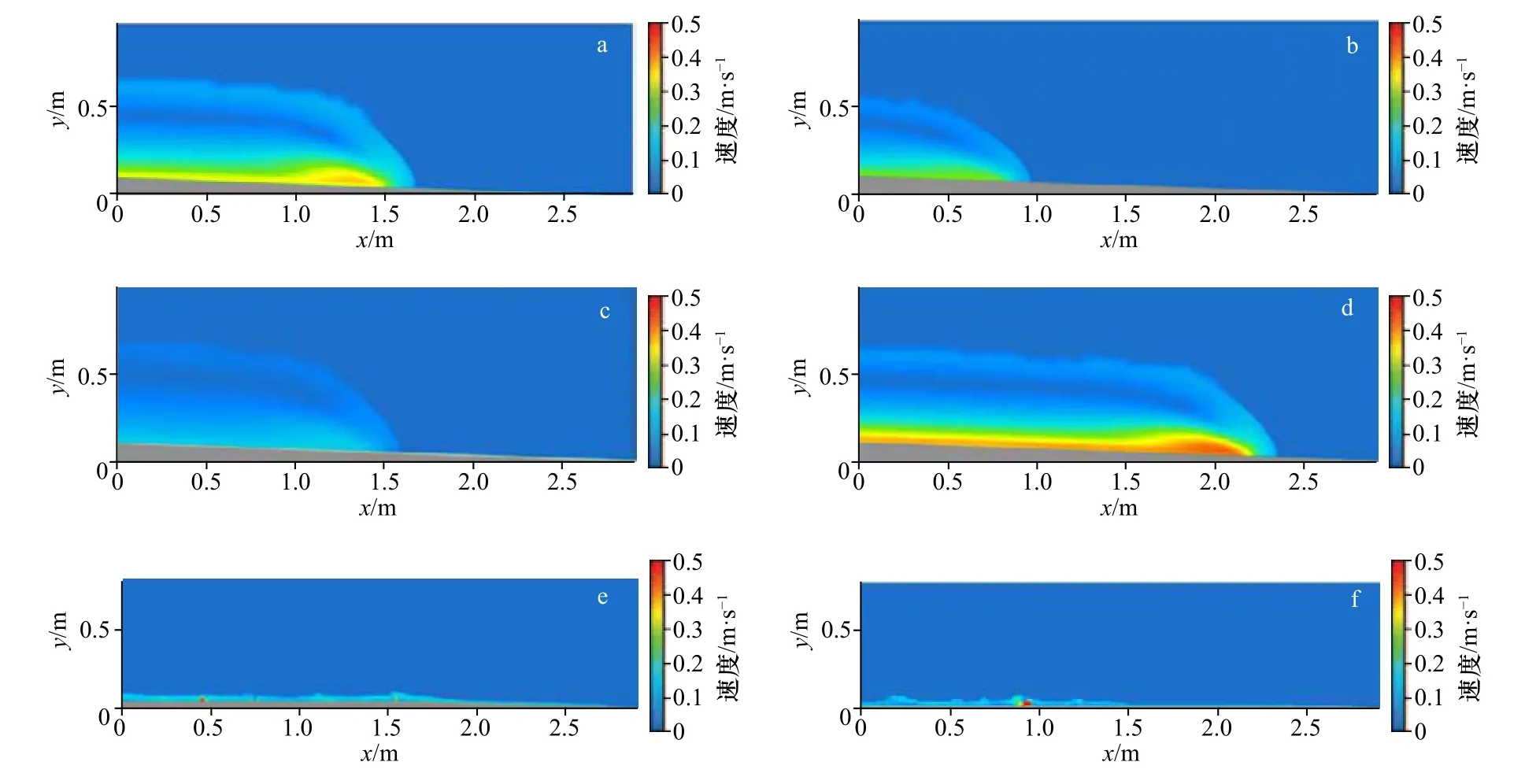
图4 200 s 时浊流头部的速度分布（图a-f 对应工况1-6）Fig.4 Velocity profile of turbidity current head at 200 s in each case (a-f corresponds to case 1-6)

3.1.2 浊流头部的密度分布

浊流头部的密度分布如图5 所示，在持续入流的浊流流动过程中，浊流头部的密度远小于浊流本体，低浓度的高速头部排开环境流体，由其后密度与浓度均较大的浊流本体推动浊流向前流动，与突然释放型浊流表现出明显差异[25]。

3.2 浊流速度特征

浊流沿斜坡流下，坡折带前坡上1 m 处的速度剖面如图6 所示，接近海床处存在速度的极大值，向上速度逐渐减小，至浊流顶层存在反向加速现象。该速度拐点由浊流扩散至环境流体中的“云状拖曳”所贡献，其速度一般较小。

斜坡上浊流受重力作用加速，一定的粒径范围内（黏土与粉砂），粒径（图6a）与初始入流速度（图6b）对流速影响较小，速度变化在0.05 m/s 之内。但粗砂颗粒浓度使流速表现出较大差异，流速变化可达0.10 m/s（图6c）。初始入流速度与浊流厚度呈正相关（图6b），但粗砂驱动的浊流厚度远小于细粒悬浮物驱动的浊流厚度，速度较细粒沉积物的速度小0.07～0.09 m/s，且不同粒径粗砂驱动的浊流的速度曲线近乎重合（图6a）。

坡度转换后，浊流发生水力跃变，跃变期间速度较坡前减小50%或以上（图7），该数值与Muck 等[35]计算结果相同。浊流的速度剖面随粒径表现出不同特征，粗砂驱动的浊流由于粒径过大，环境水体夹带系数过低，呈现薄而尖锐的特征（图7a）。粉砂与黏土驱动浊流随速度增大，浊流厚度减小（图7b），随入流浓度增大，浊流厚度也随之增大（图7c）。

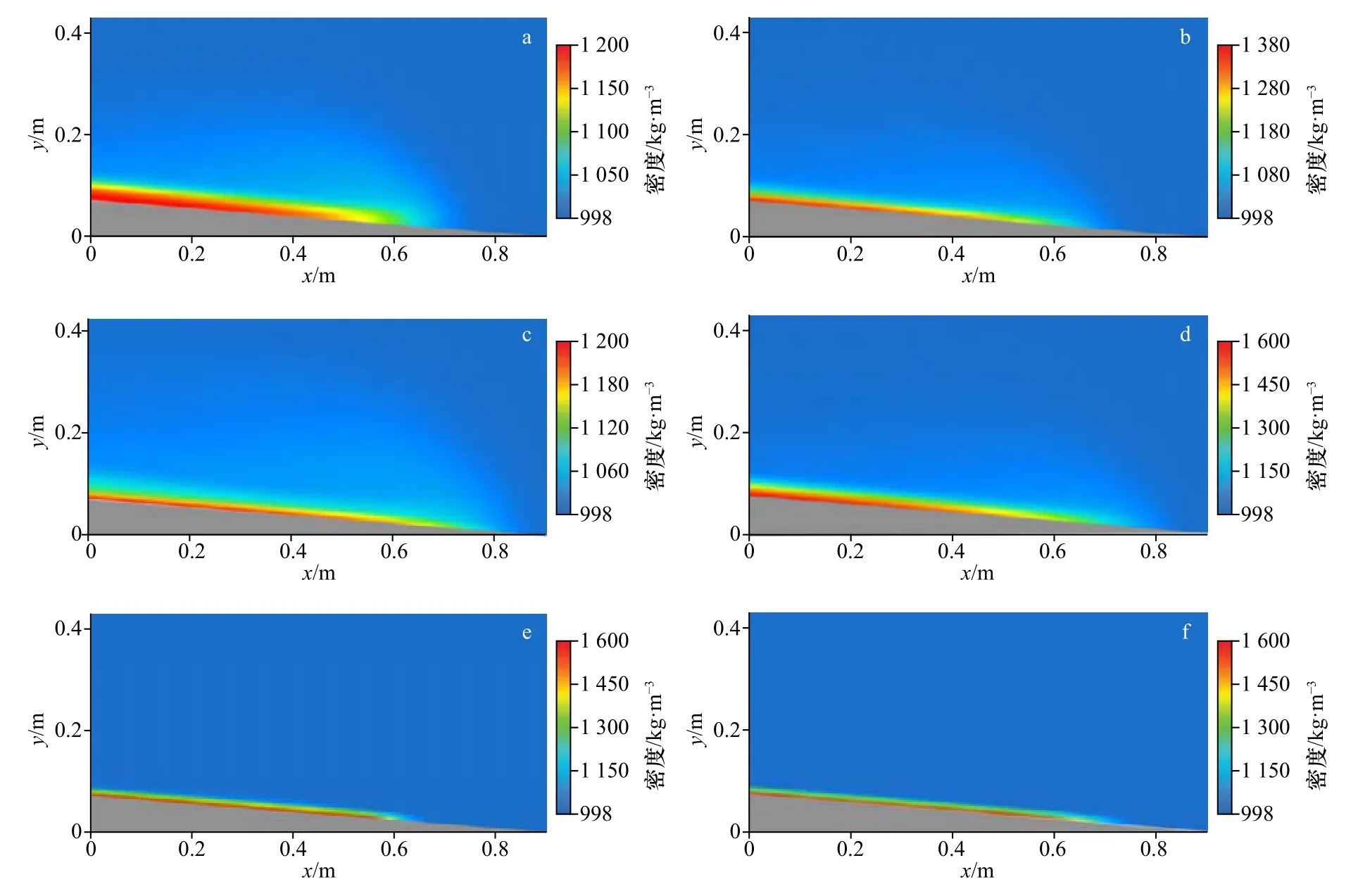
图5 200 s 时浊流头部密度分布（图a-f 对应工况1-6）Fig.5 Density profile of turbidity current head at 200 s in each case (a-f corresponds to case 1-6)

浊流在水平段流动一段时间后，海床的摩阻作用使浊流速度不断减小，悬浮颗粒逐渐沉降，粉砂与黏土的速度剖面逐步趋于一致（图8）。低速低浓度粉砂驱动的浊流与粗砂驱动的浊流速度稳定，其原因可能是浓度与速度维持了湍流强度的平衡，使浊流几近维持匀速的状态向前流动。2°的缓斜坡使浊流在重力驱动下出现微弱的加速现象，粒径与悬浮物体积分数对速度的影响显著（图9c），粗砂驱动的浊流（1 mm）已在水平段逐渐沉积。

长时间流动后（200 s），坡折带前后4 个速度剖面结构趋于一致（图10）。粗砂（粒径0.5～1 mm）驱动的浊流维持了薄而尖锐的剖面特征，且随入流粒径增大，浊流厚度变薄。黏土、粉砂驱动浊流均为典型浊流速度剖面，粒径、悬浮颗粒物体积分数对速度的影响较大，且以浊流厚度所反映的水夹带系数可能是粒径与浓度的函数，粒径越小，浓度越大，水夹带系数也越高。

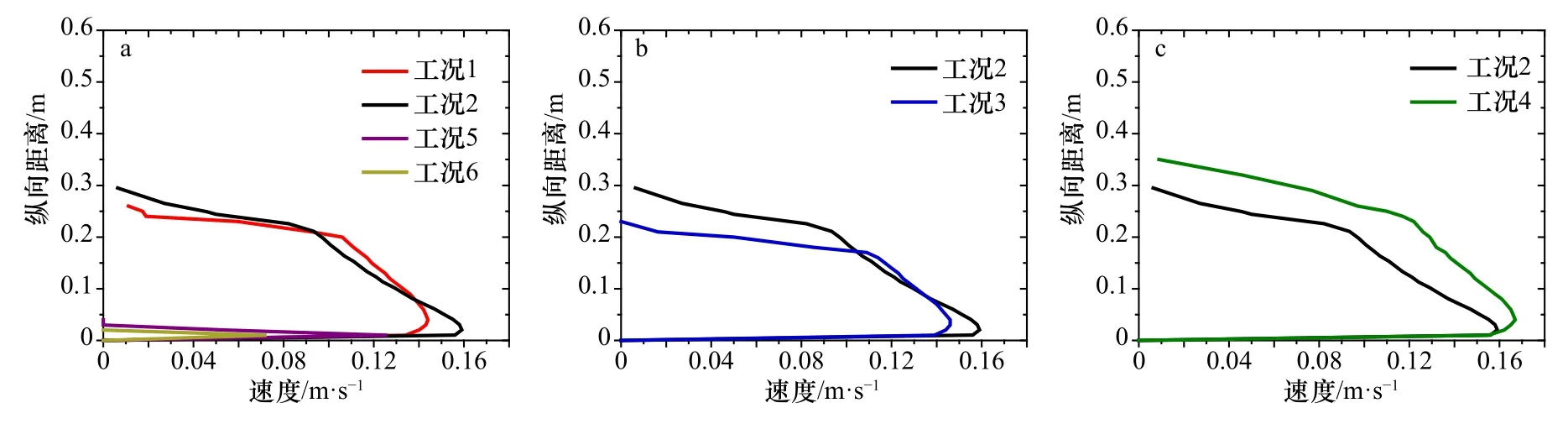
图7 浊流到达6.1 m 处垂向速度剖面Fig.7 Vertical velocity profiles at 6.1 m when turbidity current arrives

图8 浊流到达10.6 m 处垂向速度剖面Fig.8 Vertical velocity profiles at 10.6 m when turbidity current arrives

将浊流到达时刻的速度（图6 至图9）视为浊流头部速度，200 s 时流速坡折（图10）为浊流本体流速，由其最大速度对比可以看出，坡上浊流头部速度明显大于浊流本体速度（4.1 m 剖面处），平均速度高达0.10 m/s，经过破折带变化后，6.1 m 处浊流头部速度与本体速度基本相同，随浊流向前流动，浊流本体速度逐步大于浊流头部速度，其平均速度差由0.09 m/s（10.6 m 剖面处）增大至0.18 m/s（12.6 m 剖面处）。但是粗砂驱动浊流与细粒物质驱动浊流表现出不同的速度结构，自坡上至坡下整个流动过程中头部速度均略小于本体速度，但速度差很小，浊流速度结构在整个流动过程中十分稳定。

3.3 浊流的流动与沉积特征

浊流表现出坡上加速，坡折减速，水平流动后坡下小幅度加速的基本特征，且浊流厚度由于环境水体的夹带逐渐变厚。如图11 所示，坡度转换处由于速度骤然减小，湍流强度随之减小，悬浮颗粒体积浓度随之增大，表现出显著的沉积性，逐渐沉积至海床之上。由于2°缓斜坡的存在，浊流速度小幅度增加，悬浮颗粒物的体积分数短暂的下跃，但短距离的浊流运移中，高浓度浊流已然形成，小坡度不会影响浊流的流动过程，其整体仍然表现出沉积性。

细粒悬浮物由于易被环境流体夹带，故粒径与浊流厚度负相关，黏土为主驱动的浊流沉积性较弱（图11a，图12a)，速度变化幅度小，难以形成沉积记录。粉砂为主驱动的浊流沉积性较强，可能在地层上形成连续的沉积记录，而粗砂驱动的浊流由于粒径过大趋于不稳定状态，颗粒难以在悬浮状态下输运，粗砂在底床可能以滚动等方式向前输移。除非有极大的湍流强度提供粗砂的支撑力，否则浊流流动将因粗砂卸载而崩散[36]。故粗砂驱动浊流经过坡折带后，速度骤减，湍流难以对粗砂提供支撑，沉积物在坡下沉积。随流动时间和流动距离的增大，浊流速度逐渐减小，湍流强度也随之减弱，粗砂在坡下形成形似短波长的不连续的沉积物波（图11b，图12e，图12f）。

湍流强度随流速增大而增大，挟沙能力也随之越强，故流速越高沉积性越弱（图11c，图12b，图12c），反之悬浮颗粒物的体积分数越大，沉积性越强（图11d，图12b，图12d）。

图9 浊流到达12.6 m 处垂向速度剖面Fig.9 Vertical velocity profiles at 12.6 m when turbidity current arrives

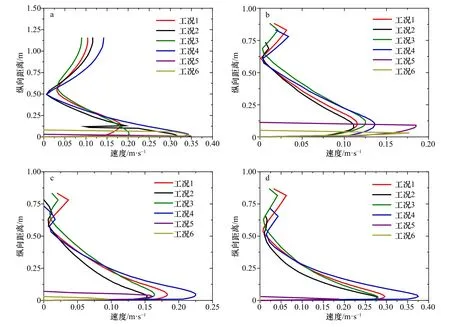
图10 200 s 时浊流在各坡折带的速度剖面对比Fig.10 Comparsion of the velocity profiles around the slope break at 200 s

4 分析与讨论

4.1 浊流结构

按动力学角度可将浊流划分为动力侵蚀带、前部调节带、沉积卸载带、后部调节带、动力平衡带5 个动力变形部分[36]，本文将动力侵蚀带与前部调节带归为浊流头部（图13），其余归为浊流本体部。

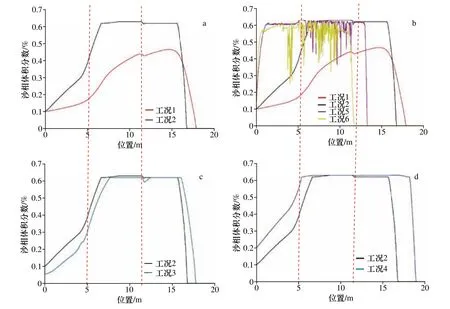
图11 200 s 时浊流悬浮颗粒在底床的体积浓度分布Fig.11 Distribution of volume fraction along the slope bottom of turbid suspended particles at 200 s

图12 200 s 时浊流在底床沉积分布（图a-f 对应工况1-6）Fig.12 Distribution of the sediments deposit along the slope bottom of turbidity current at 200 s (a-f corresponds to case 1-6)

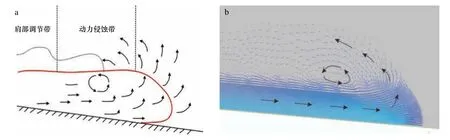
图13 浊流头部特征示意图Fig.13 Protection characteristics of turbid head

如图13 所示，浊流在流动时与周围水体的摩擦作用形成的环形涡流使沉积物呈自悬浮状态[34]，在浊流向前流动时，细粒沉积物由于流动分离作用和湍流分散压力在浊流头部产生强烈的云状拖曳现象。流动过程中，浊流头部涡流从底床裹挟悬浮物质，在调节转换带细粒物质被拖曳至云状发散层，较粗物质返回浊流底部或沉积于底床。浊流头部被高密度高速的本体部向前推动，同时补充其损失的动能与物质。故云状拖曳的强弱可能在一定程度上可指示浊流的侵蚀性，更强的云状拖曳可能指示浊流头部具有更大的湍流强度与挟沙能力，使浊流表现出更强的侵蚀性。并且近岸底流研究中发现底部流速与悬沙浓度呈正相关，悬沙通量随悬沙砂组份增加而增加[37]。因此小粒径沉积物与更高速度驱动的浊流可能具有更强的侵蚀性，大粒径沉积物表现出更强的沉积性。但由于本次模拟的浊流为单粒径驱动的浊流，与实际情况下多粒径驱动的浊流存在差异，故浊流中小粒径悬浮物比例与浊流流速可能是浊流底部再悬浮的过程响应的敏感组份，可在一定程度上指示浊流的侵蚀性。

Azpiroz-Zabala 等[38]在刚果峡谷观测到的浊流现象，如图14 所示，实测浊流头部表现出底部速度大于上部的特征，且悬浮物浓度也集中于浊流与底床相接部位，与图4 与图5 模拟浊流的头部结构特征吻合较好，且实测显示浊流头部速度小于本体流速，与模拟结果相符。但在该峡谷中实测浊流形态为中间厚两端薄，与模拟浊流形态不同。其原因可能为本次浊流模拟针对单次单粒径浊流流动，而实测浊流可能是多次浊流流动的叠加，且由混合粒径沉积物所驱动。Huang 等[25]发现连续入流型浊流与突然释放型浊流共同流入时，会出现两个涌起的头部，其形态类似2013 年刚果峡谷实测浊流，但头部汇合后的浊流形态与本文模拟相似。

4.2 浊流对地形的塑造作用

本文采用连续坡折带模型模拟陆坡峡谷-大陆架沉积扇-平缓斜坡地形上浊流的流动与沉积过程，持续入流可模拟与高浓度悬沙河流相连的海底峡谷内浊流的流动。

对比沉积结果，浊流在坡度转换后由于湍流强度随流速减小而减小，浊流携沙能力随之减弱，加之悬浮物的自然沉降，流动一段距离后悬浮颗粒物逐渐沉积于海床，与姜涛等[29-30]的模拟结果相同。粒径与沉积物位置成正比，粒径越小，距坡脚的沉积距离就越远（图12a，图12b，图12e，图12f），沉积记录越连续，粗砂在坡脚形成形似沉积物波的不连续沉积记录。浊流在具有坡度变化的地形流动，倾向沉积在斜坡的上游[29-30]，在后续多频次、长时间的浊流流动中，随浊流的不断叠加，先沉积的颗粒被压实，后沉积的颗粒受到沉积地形的影响，沉积体表现出向坡脚上游迁移的趋势[30]，这与本文模拟的间歇式入流浊流沉积结果（图15）与观测的迁移特征一致[39]。

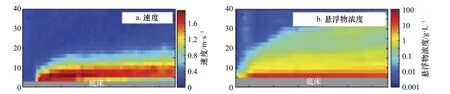
图14 实测浊流头部速度（a）与悬浮物浓度（b）[38]Fig.14 Velocity (a) and suspended sediment concentration (b) of turbidity head[38]

图15 两次间歇性持续入流浊流的沉积分布Fig.15 Sediment distribution of twice continuous inflow turbidity current

由于在实际流动中，浊流往往以间歇式多频次的方式在海底触发，故本文针对单粒径驱动的间歇式两次入流的浊流进行了模拟，流动时间为200 s，间歇为50 s。模拟结果如图15 所示，在两次浊流流动中，浊流先后沉积于底床之上，并且流动过程中，第二次浊流活动对已有的浊流沉积体前坡先侵蚀后淤积，最后呈现出中间薄两边厚的沉积形态（图15），且沉积体表现出向坡脚迁移的趋势。本次模拟的单粒径驱动的间歇式浊流与实际的浊流流动情况存在一定差异。在实际的浊流流动中，每层沉积体均应遵循粗粒物质沉积在下，细粒物质沉积在上的鲍玛层序。若流动时间足够长，且沉积序列得以保存，多次持续入流的浊流沉积在纵向上应是多个不连续鲍玛层序的叠积，每一层沉积体都表现出底部粗上部细的沉积特征。但在实际过程中，多次持续入流浊流的时间间隔可能很小或浊流痕迹被后续的流动侵蚀，故在地层上整体表现出下粗上细的沉积特征。

2009 年在台湾枋寮峡谷中观测到的浊流现象被广泛认为是持续入流的浊流活动，其沉积物短柱样品可以指示持续入流浊流的沉积特征。沿峡谷走向获取的沉积物短柱样品[40]，分别位于峡谷头部以及距峡谷头部13 km、21 km、26 km 处，其中，用210Pb 活度的异常增大指示浊流活动，粒度中的粗砂可以指示该次浊流的沉积特征（图16）。

如图16 所示，位于峡谷不同部位的短柱样按粗砂体积分数可划分为不同的层级，以体积分数的反向减小指示浊流沉积层次并以颜色划分。峡谷头部（ORI-915-MV）浊流处于加速状态，表现的沉积性较弱，而位于大陆架的短柱样（S.09、915-8、915-9）均表现出明显的浊流沉积。粗砂表现出的尖锐峰值（图16c）可能是由于后期的浊流活动将前次浊流沉积的细粒物质冲刷，使粗砂粒度图在下半段表现出倒序结构。且随浊流流动，陆坡物质随浊流携带沉积，使沉积中粗砂的体积分数减小（图16d）。

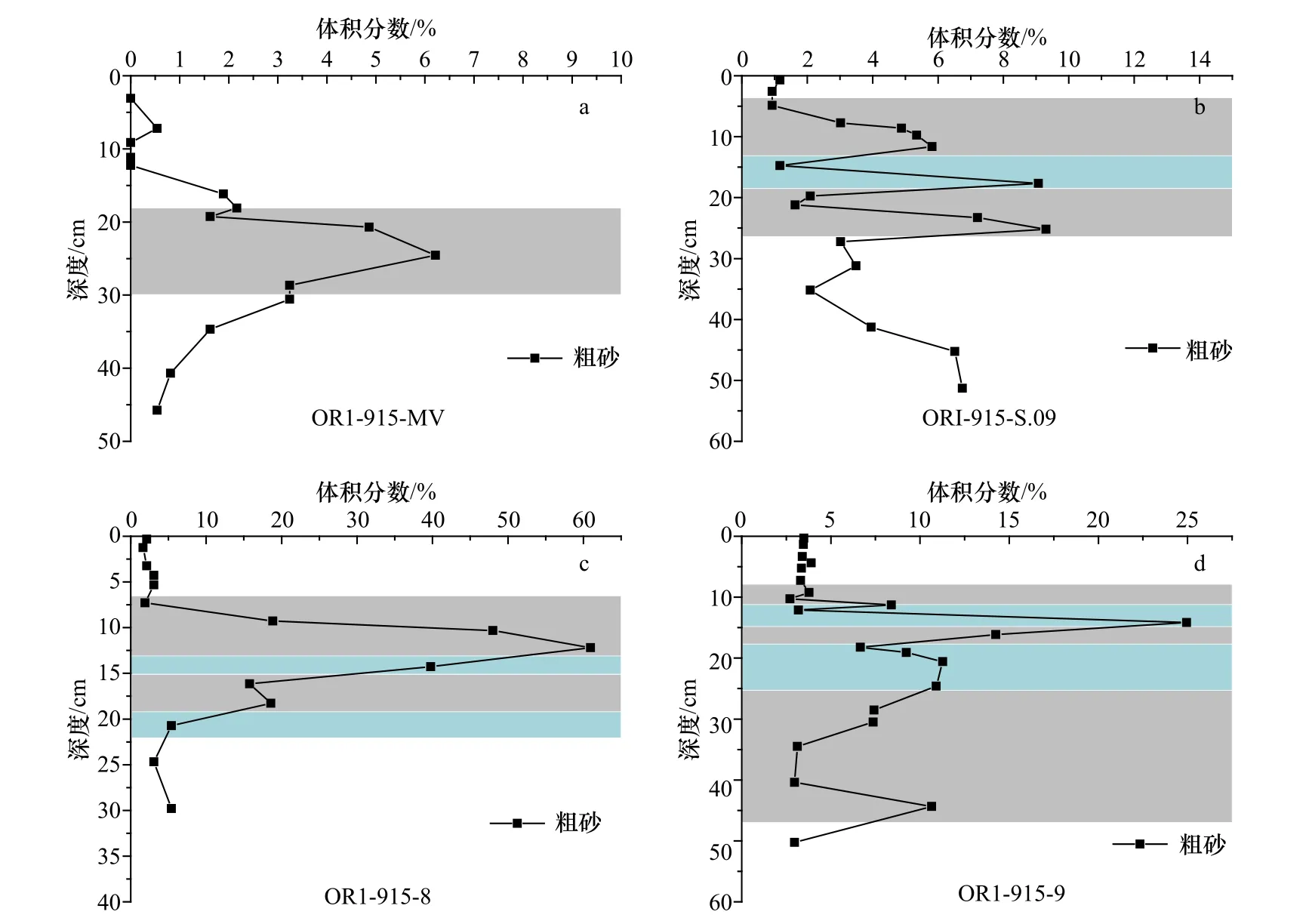
图16 枋寮峡谷粗砂粒度分布[41]Fig.16 Volume fraction of sand in the Fangliao Canyon[41]

2009 年，枋寮峡谷柱状样品的沉积特征在图16中可大致划分对应的沉积位置，从实测数据与模拟数据可以看出多频次间歇式持续入流的浊流在纵向地层上可能形成多个不连续鲍玛序列的韵律性叠积。

5 结论

本文基于不可压缩的Navier-Stokes 方程与湍流k-ε 模型构建了含有沉积物的浊流数值计算模型，应用此模型模拟了单粒径沉积物驱动的浊流在连续坡折地形上的流动与沉积过程，所得主要结论如下：

（1）浊流在峡谷中呈加速状态，流至地形平缓处速度骤减，悬浮沉积物浓度随之加大并随流动逐渐沉积，此后保持沉积状态，缓斜坡的加速作用不影响浊流的沉积趋势，陆架坡折带可能是浊流沉积作用的重要分界线。

（2）持续入流的浊流头部具有速度快、浓度低的浊流特征，在流动过程被高速高浓度的浊流本体推动向前流动。

（3）多频次入流的浊流在地层上连续叠加沉积，在垂向上可能形成多个不连续鲍玛层序的韵律性沉积。

本文的模拟结果确认了一些已知的实验事实，并且提供了浊流在陆坡峡谷-大陆架沉积扇-平缓斜坡地形下的流动及沉积特征，这对理解和推断浊流深水沉积过程具有一定的参考价值。但在浊流模型的建立和参数选择过程中，进行了适当的简化，如尚未考虑浊流与冲蚀底床的物质交换，对浊流侵蚀量的模拟尚待进一步研究。