基于时序相关性分析方法的浮标异常数据识别

张宇 ，周燕，陶邦一,3*，顾吉星，赵传高，郝增周，张艺蔚,5，黄海清，毛志华

(1.自然资源部第二海洋研究所 卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2.浙江省海洋科学院，浙江 杭州 310007；3.南方海洋科学与工程广东实验室，广东 广州 511458；4.国家海洋局烟台海洋环境监测中心站，山东 烟台 264006；5.中国科学院上海技术物理研究所，上海 200083)

1 引言

海上浮标是获得长时序、高精度海洋环境参数最主要的手段，确保浮标数据的质量可靠性是开展数据应用所面临的首要问题，因此开展浮标异常数据的检测识别是其中一项重要工作[1]。异常数据一般指超过正常合理数值范围的以及偏离由海洋环境引起的变化规律的数据[2]。将台州大陈（TZ01）和温州南麂岛（NJ01）的两个浮标叶绿素数据与Aqua/MODIS、VIIRS和GOCI 海洋水色卫星反演的叶绿素产品进行比对（图1），研究发现浮标反演的叶绿素产品存在两种异常类型：（1）浮标数据在时序分布上连续且与卫星数据有较好的一致性（图1a），但由于海洋随机过程产生如图1a 中红色方框标记的跳变数据，属于传统意义上的跳变异常数据类型；（2）红色条带标记的一段浮标叶绿素测量异常数据呈现出：在时序变化过程中连续平稳，但随时间逐渐推移，最后整体偏离正常数据的分布特征（图1b），这种异常数据属于一种新的渐变异常数据类型。基于海洋环境要素时序数据分布平稳的假设[3-6]，传统的异常数据统计识别方法仅对跳变异常数据类型的数据检测有效，而对渐变的质量异常数据类型无法识别[5-12]。主要原因在于异常发生的初始阶段，其变化特征与由海洋环境变化引起的变化趋势很难在没有先验知识的条件下进行区分，只有利用后续正常数据分布特征等后验证知识进行识别。这类渐变异常数据可能与传感器探头受污、供电异常等因素有关。渐变的异常数据类型在长时间观测的浮标数据中时有发生，因此如何在这一类型异常数据发生的初始阶段进行有效识别，对于浮标异常的实时监测、及时维护、保证数据的可靠和连续性具有现实意义。

图1 浮标数据与卫星数据叶绿素a 浓度对比Fig.1 Comparison of chlorophyll a concentration between buoy data and satellite data

国内外都已开展海上浮标观测应用工作多年，但实际上实现各类型异常数据的自动检测识别仍有较大难度[3-4]，国内对海洋数据的检测主要依赖专家经验、历史资料以及常识形成的海洋环境监测数据检验标准库[5]。目前已有的异常检测方法主要有极值检验、一致性判断、递增性判断、格拉布斯检验、狄克逊检验、拉依达检验、过度梯度检测、尖峰检测和无梯度检测等[1,6-19]，这些异常检测方法主要是针对单一参数在某一时间尺度的平稳随机过程中进行统计学的分析处理，在传统跳变异常数据类型识别中取得了较好的检测效果，但对于渐变异常数据类型的自动检测识别研究较少。

随着技术发展，目前浮标平台上搭载的传感器数目和测量的参数越来越多，而在这些测量参数中存在某些参数相互关联的特征。多元时间序列数据分析方法（如建立矢量自回归（VAR）、多元谱分析，广义自回归条件异方差模型（GARCH）等）被广泛地应用到质量异常数据的检测和识别上[20-23]。Tsay[24]将4 种类型单参数时间序列异常数据识别方法拓展到了多元序列数据。此外，异常质量数据检测中也应用到了矢量自相关性系数、差分整合移动平均自回归模型、遗传算法等方法[25-29]。然而，上述方法主要适用于跳变异常数据的识别，而且对数据平稳性要求较高、计算流程复杂，并未在本文发现的渐变异常数据类型上得到应用。其中，在海洋多元长时序数据异常识别方面，Schuckmann 等[12]提出相关性分析方法成功地识别了叶绿素浓度高而溶解氧浓度低的错误数据类型。在浮标数据质量控制中的应用，仅给出了白天叶绿素浓度高而溶解氧浓度低的错误数据类型的识别案例。窦文洁等[18]则根据海洋碳酸盐系统中海水CO2分压本身于水体温度盐度存在定量相关性关系的特点，在假设观测参数变化在非常小的时间尺度内为一平稳过程的基础上，提出了基于多参数观测序列差分统计特征的异常点识别方法。虽然该方法由于仅基于参数平稳性假设而无法进一步有效识别渐变异常数据类型，但相比于单一参数分析方法，利用多参数强关联性对异常数据进行检测，会对数据的处理有更加全面、深入的把控。

目前，我国常规生态浮标通常会同时观测酸碱度（pH）、溶解氧（DO）浓度以及叶绿素a（Chla）浓度等数据。大量的研究表明，它们之间虽然具有较紧密的相关性[30-31]，特别是在海水藻类生长暴发期间[31]，但它们并不存在稳定的相关关系，如谢群等[32]在流沙湾得出溶解氧浓度与叶绿素a浓度成正比例关系，尤其是冬季，海水中的溶解氧浓度与叶绿素a浓度具有极显著正相关，春季次之，夏秋两季两者之间不存在相关性的结论。可见在不同海域、不同季节及不同海洋过程中的参数之间相关性特征具有明显的差异性，并不能类似于Schuckmann 等[12]采用事先设定的相关性特征进行多年长时序数据的处理。Hollinger 和Richardson[33]在海洋数据不确定分析时提出了“单塔日变化法”，其基本假设是相邻日期间在相同或相似的环境条件下数据变化过程相似。因此本研究认为，浮标观测到的正常多参数数据不仅单一参数在时序变化上平稳连续，并且两两参数间的相关性在一定时序上稳定甚至一致。

本文基于上述假设，希望通过对浙江沿岸海域浮标多年的pH、DO 浓度、Chla浓度数据相关性进行分析，了解当某一参数出现渐变异常时，与其他参数的相关性特征的变化规律，基于多参数相关性变化提出一种简单、适用的渐变异常数据检测识别方法，并且探讨该方法在该海域的适用性。

2 数据来源

浮标数据采用浙江省沿岸的温州南麂大沙岙（NJ01）、台州大陈（TZ01）、宁波南韭山（NB01）、宁波渔山（NB03）、舟山嵊泗绿华（ZS03）和舟山普陀东极（ZS04）6 处浮标数据，浮标分布如图2 所示。

观测时间在2012 年8 月至2017 年5 月之间，数据每15 min 或1 h 传输1 次，以同一浮标同一时间获取的数据为一组，共计183 967 组数据，其中状态显示异常、故障或维护的数据有8 662 组，仪器运行正常状态的原始浮标数据（DO 浓度、Chla浓度和pH）有175 305 组，占总数据量的95%，数据情况如表1 所示。对仪器运行正常状态的175 305 组数据进行分析处理，对其他状态的数据不予处理。

3 基于相关性的渐变异常数据识别方法

本文根据pH 与DO 浓度具有正相关关系，Chla浓度与pH 和DO 浓度的关系因藻类生长、季节变换等因素呈现显著正相关或不相关关系等特点，利用最基本相关性统计学方法来计算pH 与DO 浓度、pH与Chla浓度、DO 与Chla浓度两两相关性系数。在对生态浮标数据进行多参数协同分析后发现，异常判定方法的关键是相关性计算时所要选取的时间窗口以及基于相关平稳性异常的判定方法。

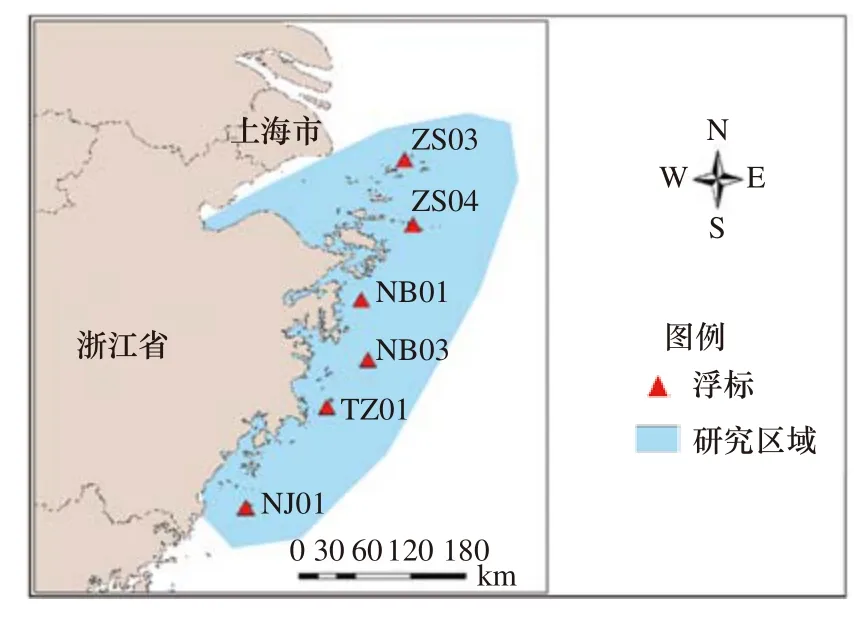
图2 研究区域浮标分布Fig.2 Distribution of buoys in the study area

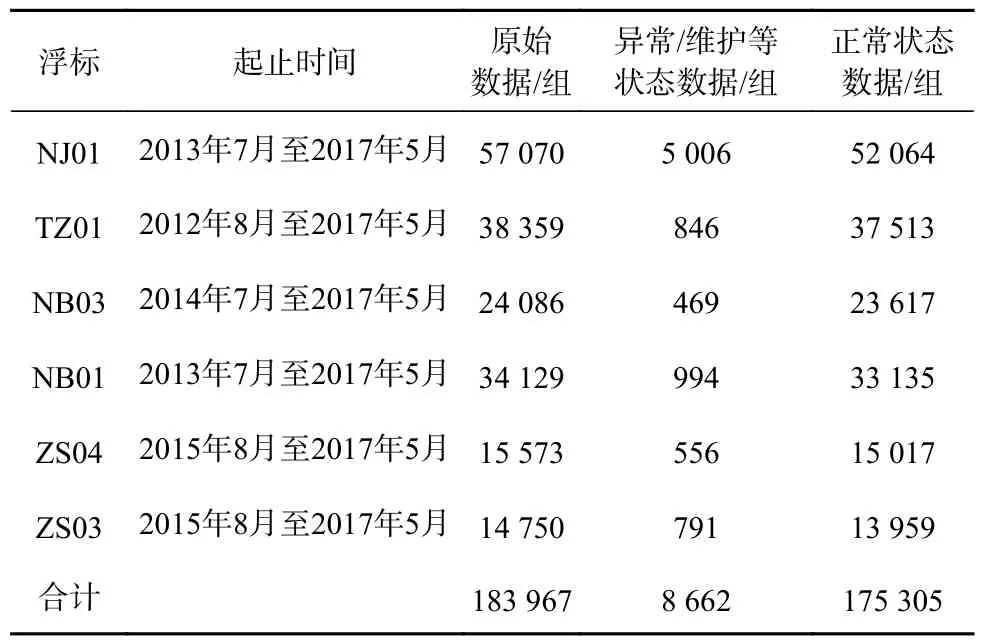
表1 浮标数据统计Table 1 Statistical buoys data

3.1 时间窗口的确定

由于浙江沿岸海域生化参数日变化动态范围较大，如以太短或者太长的时间段内的两两相关性来建立成段异常数据方法，则存在较大的随机与不确定性，不利于对长时序浮标数据的稳定性研究与渐变异常数据的早期识别。因此，选择合适的时间窗口，对于建立相关性分析处理异常数据模型至关重要。本文将浙江沿岸6 处仪器运行正常状态的175 305 组浮标数据经过不可能出现的范围和5S 方法剔除异常数据等预处理后，剩余156 305 组浮标数据参与多参数协同分析。其中，选出13 620 余组各参数质量较好的浮标数据对其进行两两相关性分析。部分正确的浮标数据序列如图3 所示。

将图3 的pH、DO 浓度和Chla浓度数据的两两相关系数（Rnd）计算的时间窗口逐天扩大，从1 d 扩大到16 d，结果如图4a 所示。由图可见，随着时间窗口的扩大，相关性逐步提升，并且当扩大到8 d 时Rnd都处于稳定状态，即当时间窗口大于8 d 后相关性并未明显增强。同时以8 d 为时间窗口对图3 中的多组浮标长时序数据进行8 d 两两相关系数（R8d）的计算（图4b），可以看出正常原始浮标数据的R8d在一定时期内同样非常稳定，因此时间窗口选定为8 d，同时将R8d作为检测渐变异常数据的核心参数。

3.2 基于相关性的异常判定方法

图3 部分正确的浮标数据序列Fig.3 Partially correct buoy data sequence

图4 不同时间窗口的相关系数（a）和基于8 d 时间窗口的相关系数（b）Fig.4 Correlation coefficient for different time windows (a),and correlation coefficient for 8 d time window (b)

首先，利用多参数之间相关性程度来进行异常数据判定。如图4b 所示，正常数据的R8d变化平稳，状态稳定。为定量化正常R8d变化的范围，利用6 处浮标多年中的正常数据集，统计了浙江海域R8d的数值分布情况，如图5 和表2 所示。统计结果表明：（1）pH与DO 浓度之间正相关性最强，几乎所有正常数据的R8d(pH-DO)都大于0；（2）DO 浓度与Chla浓度之间相关性次之，其R8d(DO-Chla) 大于-0.3，其中大于0 的数据近95%；（3）pH 与Chla浓度之间相关性变化较大，但有92% 数据的R8d(pH-Chla) 大于0，另6.8%的R8d(pH-Chla)数据在-0.3～0 之间，并且仅有1.2%的R8d(pH-Chla) 小于-0.3。因此，（1）正常数据pH 与DO 浓度、pH 与Chla浓度、DO 浓度与Chla浓度明显存在较高的正相关关系，其判定原则较为简单，即两项以上的相关性R8d都大于0.5 可以作为数据正常有效标志；（2）因pH 与DO 浓度之间不存在负相关关系，明显错误数据的判定原则为当R8d(pHDO)＜0 时为异常值；另外当R8d(pH-DO)＞0 时，如果Chla浓度与DO 浓度、pH 之间不存在较强的负相关关系，即R8d(pH-Chla)＜-0.3 时，或R8d(DO-Chla)＜-0.3，可识别为可疑数据。实际上，单一的R8d只能用于识别相对明确的正确及异常数据，而对于其中某项相关性R8d小于0.5 的浮标数据需要进一步采用其他相关性时序稳定性指标来进行识别。

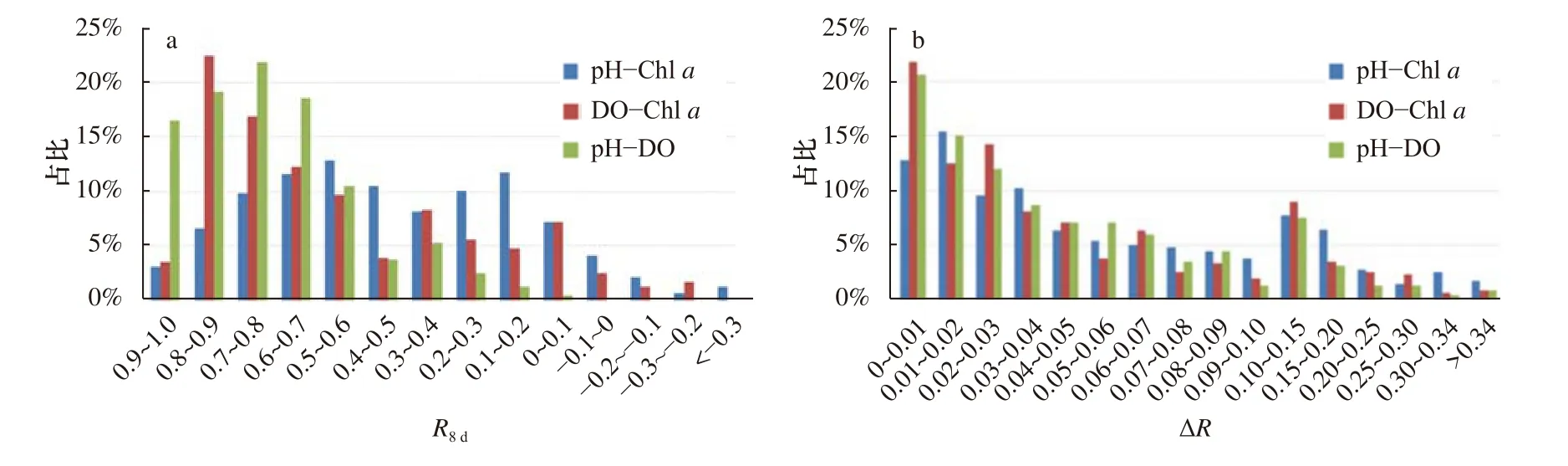
图5 R8d（a）和ΔR（b）的分布情况Fig.5 Distribution of R8d (a) and ΔR(b)

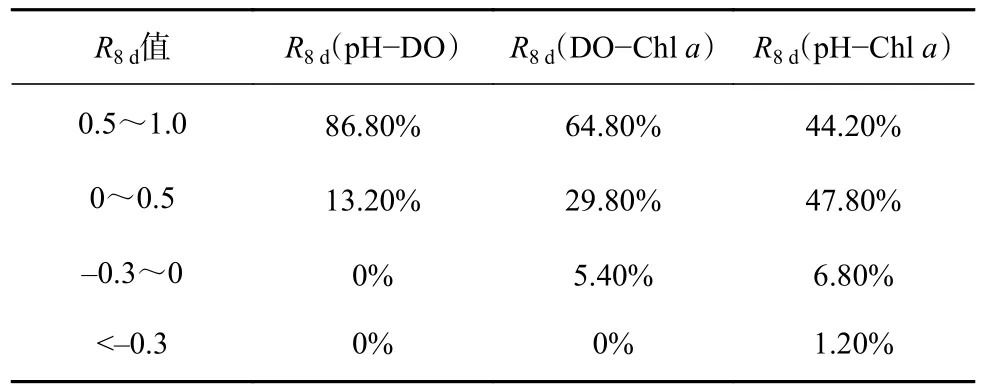
表2 R8d 的分布情况Table 2 Distribution of R8d

如前文所述，本文认为正常浮标多参数数据之间的两两相关性在一定时序上是稳定甚至是一致的，因此需要建立一个指标来表征R8d本身的稳定性。本文利用前后两天R8d之差的绝对值（ΔR）作为判断相关性时序分布稳定与否的指标。通过统计正常浮标数据的ΔR分布情况（图5b，表3）可见，其中约有60%～70%数据的ΔR＜0.06，且ΔR＜0.1 数据都达到了77.6%以上。从数据分布上可以看出，正常浮标数据的多参数之间相关性变化是稳定或缓变的过程，符合前文的稳定性假设。由于计算求得ΔR的标准差为0.068，同时从表3 的统计结果也可看出，各相关性中ΔR＞0.34的数据仅占1.0%左右，因此选取5 倍标准差[19]即0.34为判断稳定性阈值，即当0＜R8d(pH-DO)＜0.5，-0.3＜R8d(DO-Chla，pH-Chla)＜0.5 时，有一项ΔR＞0.34则判定为异常值。

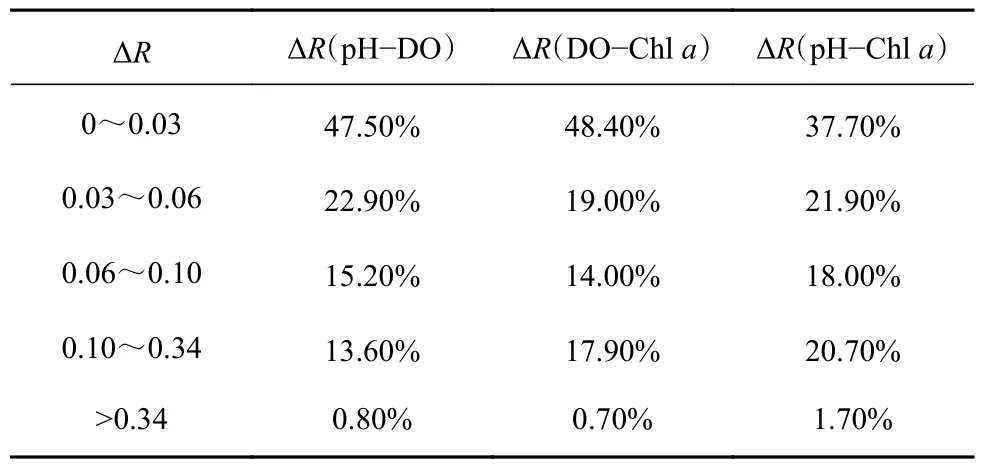
表3 ΔR 的分布情况Table 3 Distribution of ΔR

利用R8d和ΔR两项指标进行渐变异常数据的判断与识别流程如图6 所示。第一步利用单一指标R8d来判定简单的正确数据和异常数据；第二步则是利用ΔR作为R8d稳定性指标来进一步判定异常数据。

4 结果与讨论

4.1 识别算法实例与结果对比分析

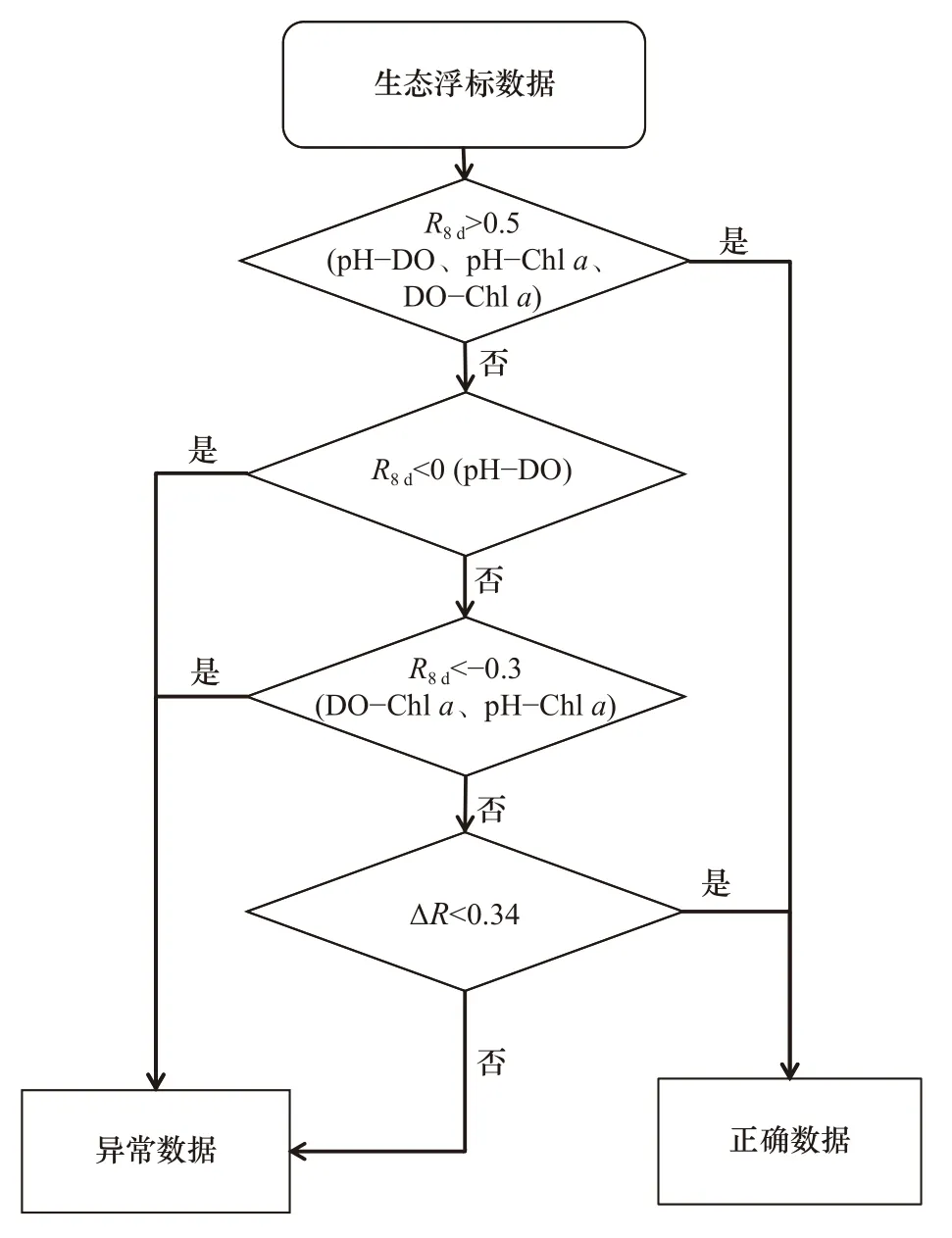
图6 数据判断流程图Fig.6 Flow chart of buoy data processing

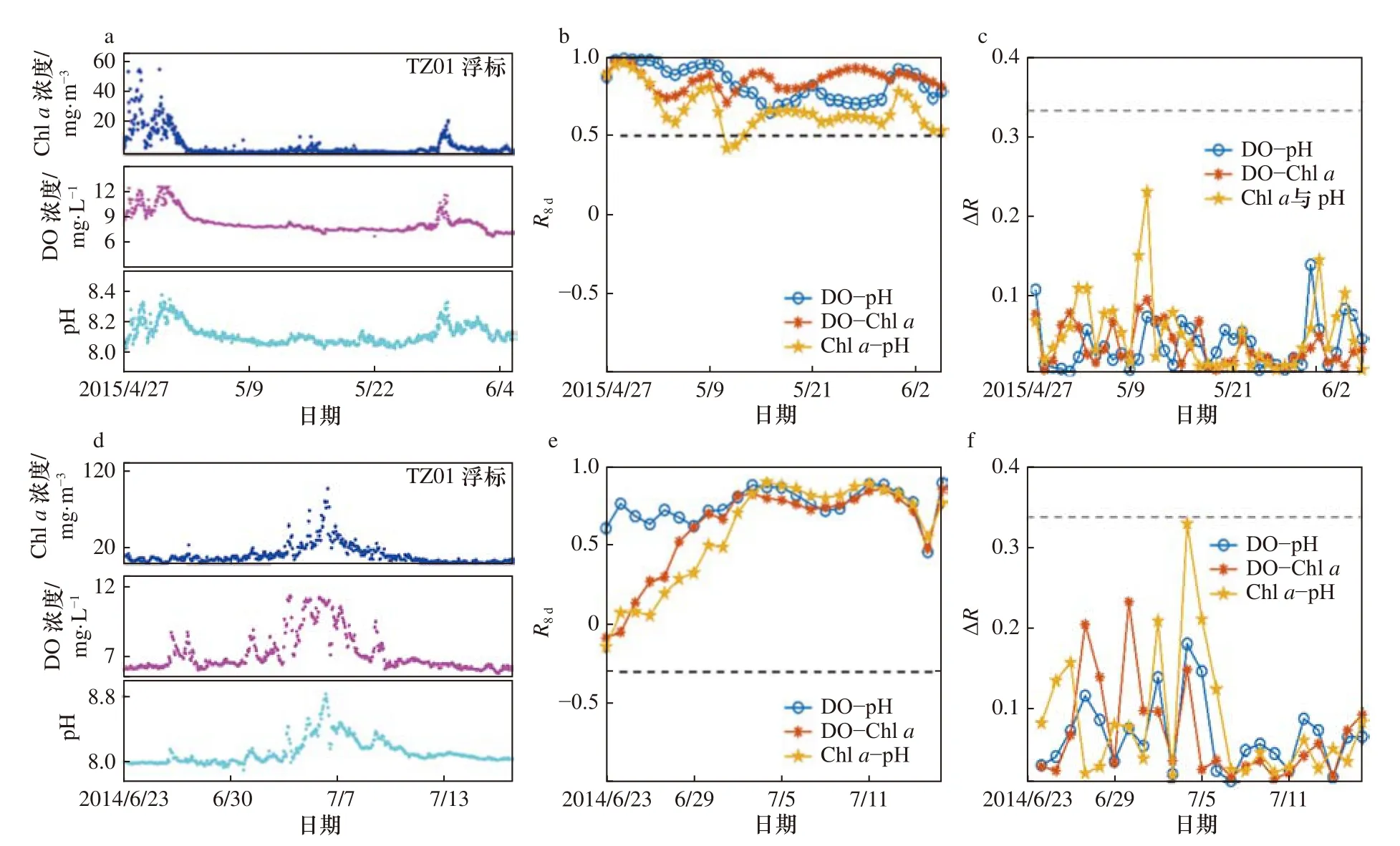
图7 2015 年4-6 月（a-c）和2014 年6-7 月（d-f）TZ01 浮标的原始数据（a，d）、R8d（b，e）和ΔR（c，f）Fig.7 TZ01 buoy raw data (a,d),R8d (b,e),and ΔR(c,f) in April to June,2015 (a-c) and June to July,2014 (d-f)

本文利用浙江温州、台州及舟山海域NJ01 浮标、TZ01 浮标以及ZS04 处浮标典型数据，对渐变异常数据的判定方法进行了适用性验证。首先，选取同样位于台州外海TZ01 浮标的2015 年4-6 月（图7a-c）和2014 年6-7 月（图7d-f）的两组正常数据。第一组2015 年的原始数据是十分具有代表性的正确数据，Chla浓度、DO 浓度和pH 之间存在非常高的正相关性，两两R8d大于0.5，并且相关性的变化平稳，ΔR都小于0.34。而第二组2014 年的正确数据相比于第一组数据变化更加复杂，从6 月下旬，Chla浓度与DO浓度和pH 存在极弱的相关性，R8d(DO-Chla)和R8d(pHChla)接近于0，但随着7 月初藻华事件的出现，上述R8d逐渐升高，并在整个藻华期间处在一个平稳的高相关性时期。虽然在这一过程中R8d的总体变化很大，但根据ΔR的计算结果都小于0.34，可以说明这个变化过程是稳定的渐变过程。那么根据图6 的识别方法仍然可以准确判定为正确数据，因此证明了本文方法的适用性。

本研究同样利用了浙江台州海域TZ01 浮标2013年5-6 月（图8a-c），以及温州海域NJ01 浮标2014 年6 月（图8d-f）和2015 年3-4 月（图8h-j）的3 组存在渐变异常的数据集对本文识别方法进行了适用性验证。

第一组案例是2013 年5-6 月TZ01 浮标数据（图8a），其中，5 月初有一次藻华事件，3 个参数变化同步浮标数据正常，而渐变异常数据实际上出现在5 月24 日前后，pH 上升发生偏离，后续在5 月30 日前后恢复正常。图8b 和图8c 分别给出了对应的R8d和ΔR数据，图中红色为异常值区间（5 月24-29 日），灰色部分为相关性计算受异常值影响区间。可以看出5 月15 日出现ΔR＞0.34 的情况，但是根据图6 判断流程，5 月15 日3 组R8d都升高到0.5 以上，因而仍然判定为正确数据。而在5 月24 日（表4），R8d(pH-DO)下降到-0.42，R8d(Chla-pH)下降到-0.39，并且ΔR(pH-DO)为0.89，大于0.34，多项指标符合本文渐变异常数据的判定标准，因此成功判定为异常数据，实现了数据异常早期识别。另外DO-Chla的R8d虽然有所下降，但仍然保持在0.5 以上。如果利用排除法，本方法可以进一步判定是3 个参数中pH 值出了问题。

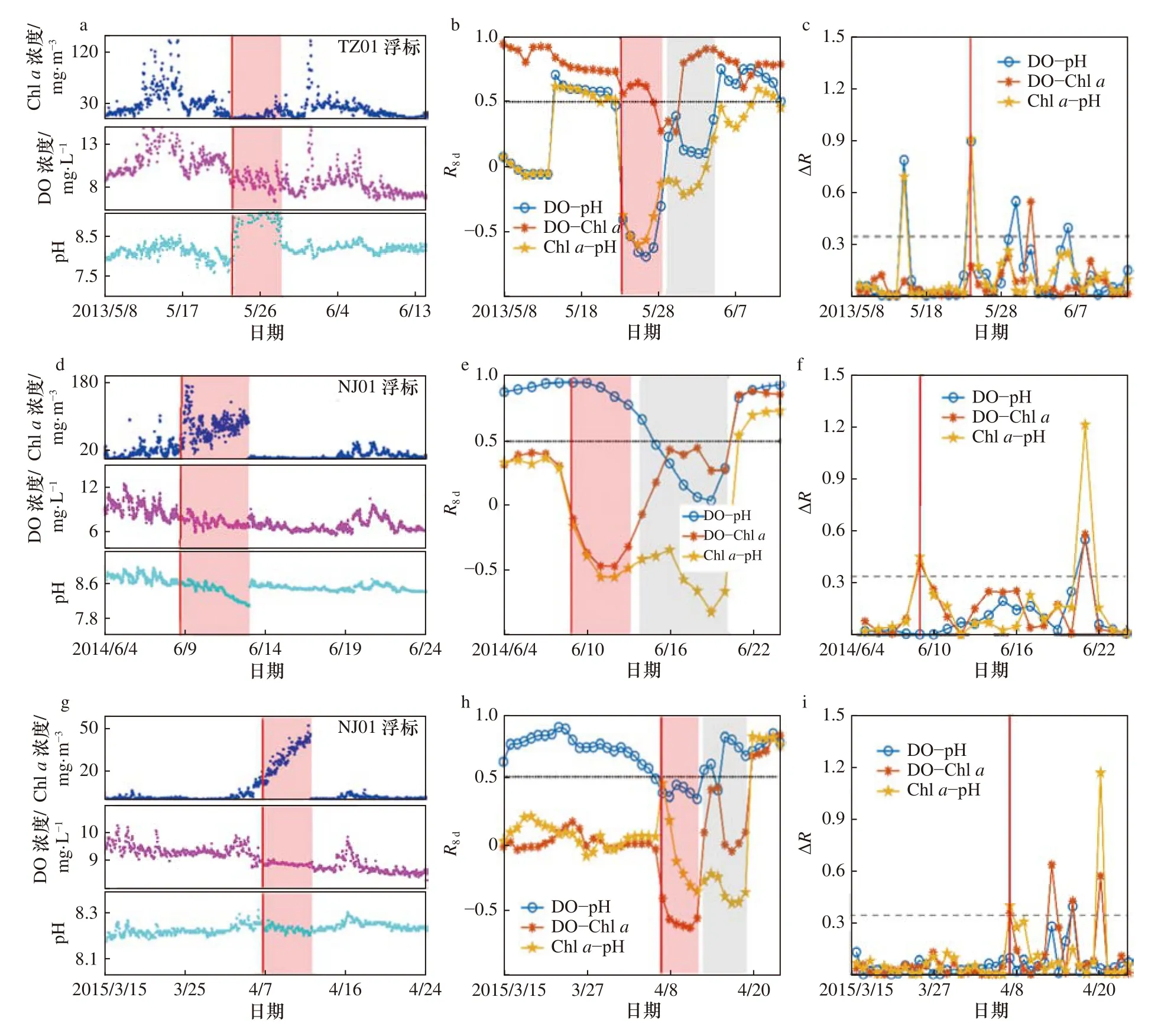
图8 2013 年5-6 月TZ01 浮标原始数据（a）、R8d（b）和ΔR（c），2014 年6 月（d-f）和2015 年3-4 月（g-i）NJ01 浮标原始数据（d，g）、R8d（e，h）和ΔR（f，i）Fig.8 TZ01 buoy raw data (a),R8d (b),and ΔR(c) in May to June,2013,and NJ01 buoy raw data (d，g),R8d (e，h),and ΔR(f，i) in June 2014 (d-f) and March to April 2015 (g-i)

第二组案例是2014 年6 月NJ01 浮标的数据，如图8d 所示渐变异常数据出现在6 月9 日前后。根据图8e 和图8f 对应的R8d和ΔR结果（表4），在6 月9 日虽然R8d（DO-Chla）和R8d（pH-Chla）的下降并未超过-0.3，但是DO-Chla和pH-Chla的ΔR分别高达0.41、0.44，皆大于0.34，故可判断出在6 月9 日数据出现了异常。根据后续Chla浓度的变化也可看出6 月9 日是异常数据出现较早时期，证明了本文方法早期识别的有效性。

表4 浮标出错日期的R8d 和ΔR 情况Table 4 R8d and ΔR of buoy error date

第三组案例是2015 年3 月和4 月NJ01 浮标数据（图8g-i），同样可以看出渐变异常数据开始出现在4月7 日的前后。然而与前两组数据不同的是，本组不同的R8d出现相反的变化趋势（表4），其中R8d（DO-Chla）降到了-0.41，而R8d（pH-Chla）却上升到了0.45，但两者的ΔR都大于0.34，最终4 月7 日被判定为异常数据起始点。通过上述多组案例的验证，本文的识别方法能够适用于浙江沿海多参数浮标数据的渐变异常类型识别。

4.2 水体生化参数变化带来滞后现象的影响

图9 2015 年9 月ZS04 浮标原始数据（a）、R8d（b）和ΔR（c）Fig.9 ZS04 buoy raw data (a),R8d (b),and ΔR(c) in September,2015

海洋水体生化特性变化并不完全同步，一些参数相比于其他参数具有滞后现象。部分大型赤潮发生时，如图9a 所示的舟山2015 年9 月25 日前后的一次赤潮事件，藻类暴发导致叶绿素峰值的出现往往早于DO 浓度或pH。这就导致在初期，叶绿素浓度与DO 浓度或pH 的R8d数值相对较小（图9b），同时随着赤潮的发展，R8d迅速升高，导致ΔR可能大于阈值0.34（图9c）。此种情况下，如果R8d都高于0.5 呈现极高正相关性亦可判定为正确数据，但是如果小于0.5 则很容易被错误识别为异常数据。在这种剧烈而快速的海洋过程中，如何有效识别正常海洋规律现象与渐变异常数据是十分重要但又极具挑战性的问题。实际上，本文采用的方法是时间同步相关性分析。如果利用时间延迟模式或许可以有效避免此类异常数据的错误识别。然而，目前对于该类滞后现象产生的海洋学机制并不十分明了。因此，在识别方法中如何具体引入时间延迟模式（如延迟区间等）还需进一步研究。

4.3 季节性（冬季）相关特征差异的影响

本文数据主要集中在上半年，而季节性变化（特别是冬季）对近海海域的海洋现象有着重要影响。由于浙江沿岸受河流冲淡水、季风和各类水团影响较大，冬季浙江沿海海域受浙闽沿岸流影响，水中悬浮泥沙含量高，限制了藻类生长。在这一时期，水体Chla浓度、pH 和DO 浓度的相关性比春、夏和秋3 个季节要弱很多。图10 为2014 年冬季（2014 年11 月至2015 年2 月）TZ01 浮标的观测结果，从图10a 可看出，3 个参数的时序变化依然连续平稳，ΔR也基本在0.34 以内（图10c），也说明了数据的平稳性，但是相关性系数R8d时高时低（图10b），甚至出现极强的负相关。主要原因是在冬季水温低，藻类丰富度较小，导致叶绿素浓度变化很小，对pH 和DO 浓度的影响作用有限。反而在这一时期，DO 浓度的变化受温度影响较大，有个缓慢上升过程。因此，冬季浙江海域的3 个参数在机理上并不存在明确的相关性，而本文方法也仅基于同一年份前序时间数据的相关性进行渐变异常数据识别，所以在冬季可能会失效。

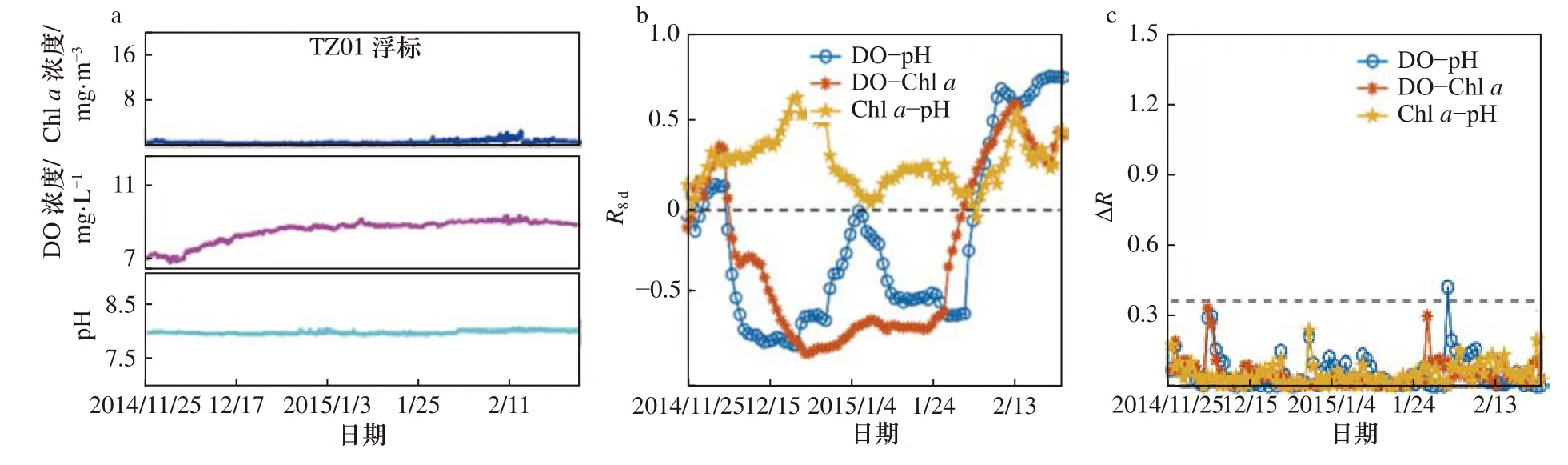
图10 2014 年冬季TZ01 浮标原始数据（a）、R8d（b）和ΔR（c）Fig.10 TZ01 buoy raw data (a),R8d (b),and ΔR (c) in the winter of 2014

在上述不适用的情况下，我们需对时序相关性的概念进一步拓展，可利用同一海域季节性数据存在物候等现象，依靠历史同一时期观测数据集等，对浮标渐变异常数据进行有效地识别。如刘增宏等[34]采用历史水文观测资料集得到的温-盐度关系对Argo 剖面浮标盐度资料进行校正，王辉赞等[35]也同样通过寻找Argo 浮标不同剖面位置与其“最佳匹配”历史剖面资料对比判别的途径，对Argo 浮标盐度偏移现象进行有效甄别。上述方法虽然用的是连续深度剖面数据，但是替换成连续时间序列数据同样适用。如图11所示，为台州大陈浮标在2014-2015 年冬季与2015-2016 年冬季的pH、DO 浓度和Chla浓度数据对比结果，可以看出这两年冬季同一时期的pH、DO 浓度和Chla浓度数据变化有较好的一致性趋势。因此利用与多年历史数据的相关性，可对pH、DO 浓度和Chla浓度数据进行异常识别。这或许是本文识别方法在冬季失效问题的一种有效解决方式，但需要大量历史数据的积累，目前还无法实现，需要进一步研究。

5 结论

本研究通过对浙江沿岸6 处浮标多年多参数观测数据进行分析，发现了与传统跳变异常数据不同的渐变异常数据类型。该异常数据类型呈现出在时序变化过程连续平稳，但随时间逐渐偏移，最后整体偏离正常数据的分布特征；并且在异常发生的初始阶段，其变化特征与由海洋环境变化引起的变化趋势很难在没有先验知识的条件下进行区分。因此本文提出了一种假设：浮标观测到的正常多参数数据不仅单一参数在一定时序上的变化是平稳连续的，并且两两参数间的相关性在一定时序上是稳定甚至是一致的。根据上述假设，本文建立了基于pH、DO 浓度、Chla浓度数据两两相关性的渐变异常数据类型自动识别方法，确定了以8 d 时间窗口的两两相关系数（R8d）作为核心相关性表征指标，并将前后两天R8d之差的绝对值（ΔR）作为判断相关性时序分布稳定性指标，形成了利用R8d和ΔR两项指标进行渐变异常数据判断与识别的流程。

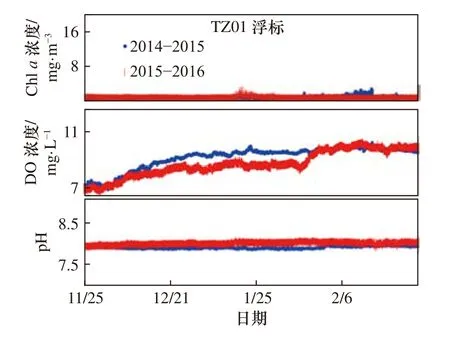
图11 TZ01 浮标冬季原始数据Fig.11 TZ01 buoy raw data in winter

本文提出的方法重点突出了多元参数间相关性系数时间序列上的变化特征，各判别指数计算过程简单、直观，易于实际浮标监测工作人员的理解和掌握。通过浙江沿海浮标实际测量数据案例检验，证明了该方法可以用于渐变异常数据类型的实时监测，对浮标的传感器渐变异常做到早期识别，特别是由生物污垢导致传感器测量值持续增加而引起的假赤潮现象，有较好的识别效果，可解决由此带来的赤潮预报虚警等问题。因此，在指导浮标日常检查与维护、确保数据的准确性和完整性方面有实际意义。本文根据单参数自校方法无法识别渐变异常数据类型，提出了一种简单，实用的有效解决方法。此方法为渐变异常值的自动识别及处理提供了新的思路。由于所处海域的不同，可能相关性稳定的时间窗口有所不同，需因地制宜，考虑季节性差异等因素的影响。因此在后续研究中应当针对在多参数变化不同步、冬季数据和非高斯分布数据等情况下，识别精度不高等局限性，可利用多年历史数据对其进行物候特征分析，提高相关性识别方法精度。