一种高升压比交错并联的DC/DC变换器

焦文良，石方园

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

在能源、环保等问题不断受到关注之时， 能量回收新能源的开发利用均受到人们的关注，无论储能用的蓄电池、超级电容、还是光伏电池，这些电池的输出等级都在50 V以下，然而储能系统或者新能源发电系统的高压侧电压等级都在几百伏以上，如何实现高增益升压是储能系统以及新能源发电系统亟需解决的问题[1-2]。

文献[3]提出无论是移动储能还是静态储能，只要系统功率大于1 kW，即可视为大容量储能。传统的BOOST电路是无法满足要求的，虽然通过调节开关器件占空比可以在理论上实现无限制升压，但在实际工况下会使电路中功率开关管和二极管的电压应力大、功率开关及二极管损耗大等问题，使传统BOOST电路的增益峰值只能在6以下[2]。

为得到高增益的电压输出，通常采用隔离型变换器，如正激、反激、半桥、全桥等变换器，通过调节占空比D以及隔离变压器的原副边匝数比就可以得到较高的输出电压。由于变压器的制作工艺，变压器的漏感无法解决，造成电路EMI较为严重，而且磁芯的体积一般较大，对于在体积要求较小场合下，隔离型变换器难以达到要求[4-5]。对于非隔离型的结构，文献[6]提出一种准Z源 BOOST 变换器，虽然其开关管占空比在0.5以下就能够得到较高的电压输出，但是功率开关、二极管的电压应力为输出电压，限制了其在较高压场合下对开关管的选型。

对于传统交错并联BOOST变换器，虽然具备电流纹波小、降低功率半导体器件的电流应力和热应力，实现冗余，提高系统运行的可靠性和功率密度的特点，但是对于降低功率开关管的电压电流应力没有实质影响，单个开关管承受的电压应力为输出电压，显然在高电压输出场合是不适用的[7]。

在上述研究的基础上，笔者设计了一种具有高升压能力的交错并联BOOST变换器，通过搭建实验样机实验证明拓扑结构具备电压变换比高、功率器件电压应力小等优点。

1 BOOST变换器

传统BOOST拓扑结构如图1所示，若在电路中加入一个电压源，如图2所示，是否可以得到高电压增益，此时电路的增益为

(1)

式中：M——电压增益；

D——开关管导通占空比；

Udc——直流电压源DC的电压大小；

Uin——输入的电压大小。

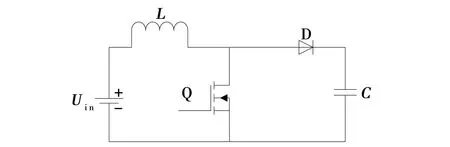
图1 传统BOOST拓扑Fig. 1 Traditional BOOST topology

通过式(1)可以发现，电路的增益得到提高，从而证明了外加电源的方式可以实现传统BOOST电路的高增益输出。根据电容特性，即在电容电压纹波较平均值很小时，可等效为电压源[4]，从而得到如图3所示的改进型高升压比交错并联BOOST结构。

图2 改进型BOOST拓扑Fig. 2 Improved BOOST topology

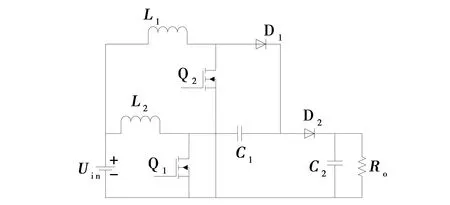
图3 改进型交错并联BOOSTFig. 3 Improved staggered BOOST

2 原理分析

由传统的BOOST拓扑升压公式及式(1)可知，当D越大时，此时电路的电压增益M也越大，而且在实际工况下，一般当增益M>4 时才考虑采用高升压 BOOST 变换器，故文中主要分析占空比D>0.5时变换器的性能，为了简化分析过程，假设[4]：L1、L2相等使电感电流连续；电路选用的器件都是理想性器件，不计寄生参数。

图4是电路在稳定工作状态下(D>0.5)的主要波形，图5为不同的工作阶段的等效电路模型。由图5a可见，开关管Q2、二极管D2导通，开关管Q1、二极管D1处于关断状态，此时电感L1吸收能量，电感L2释放能量， 电容C1放电，电容C2充电，此时有电感电流iL1不断增大，电感电流iL2不断减小，电容电压uC1不断减小，直到t1时刻，此过程结束[4]。

由图5b可见，此时开关管Q1、Q2同时导通，二极管D1、D2同时关断，电感L1、L2同时吸收能量，输出电压由电容C2提供，则电感电流iL1开始增大，iL2继续增大，电容C1由于未参加电路的充放电过程，因此电容电压保持不变，此过程直到t2时刻结束[4]。

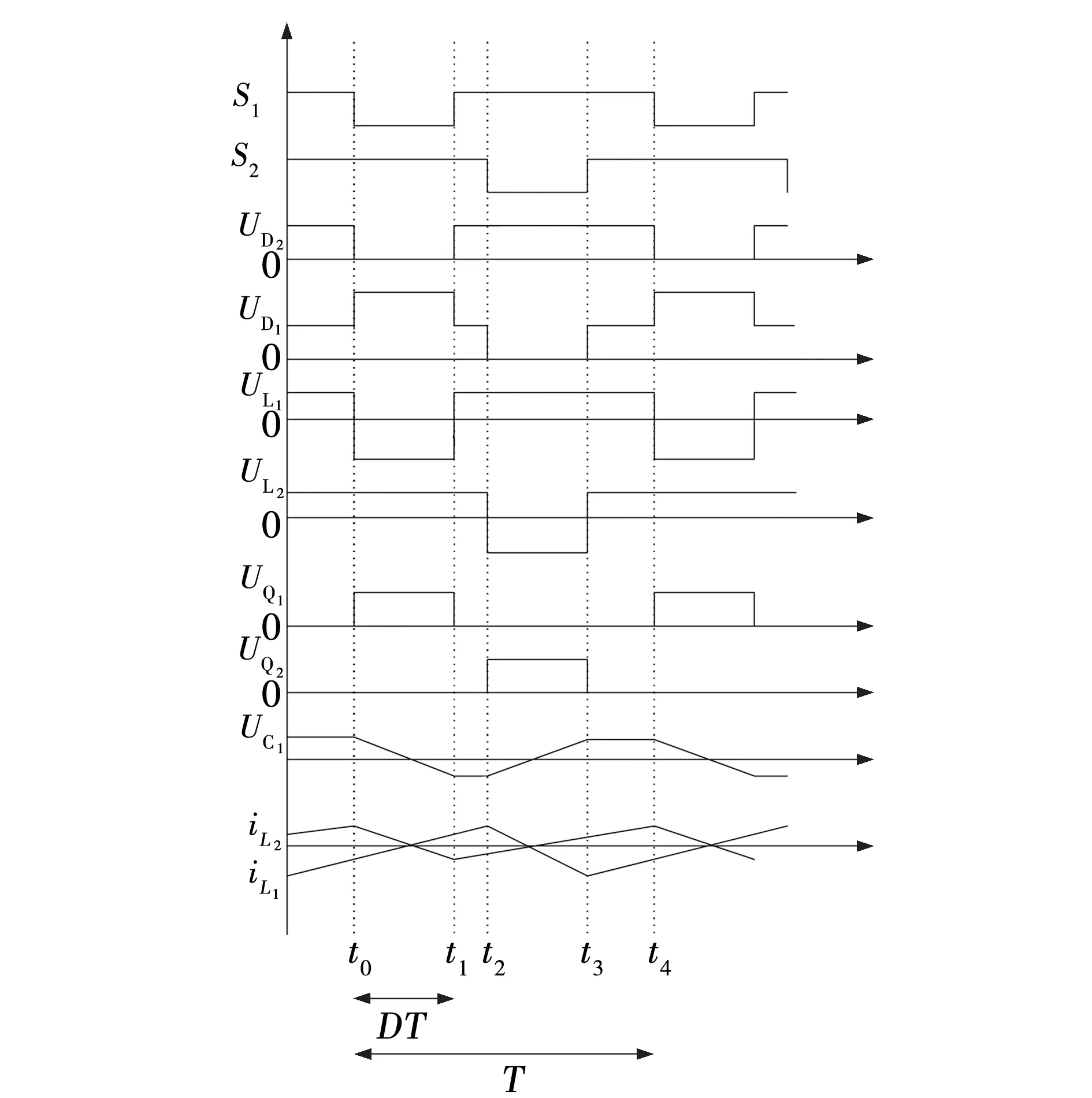
图4 主要波形Fig. 4 Main waveforms

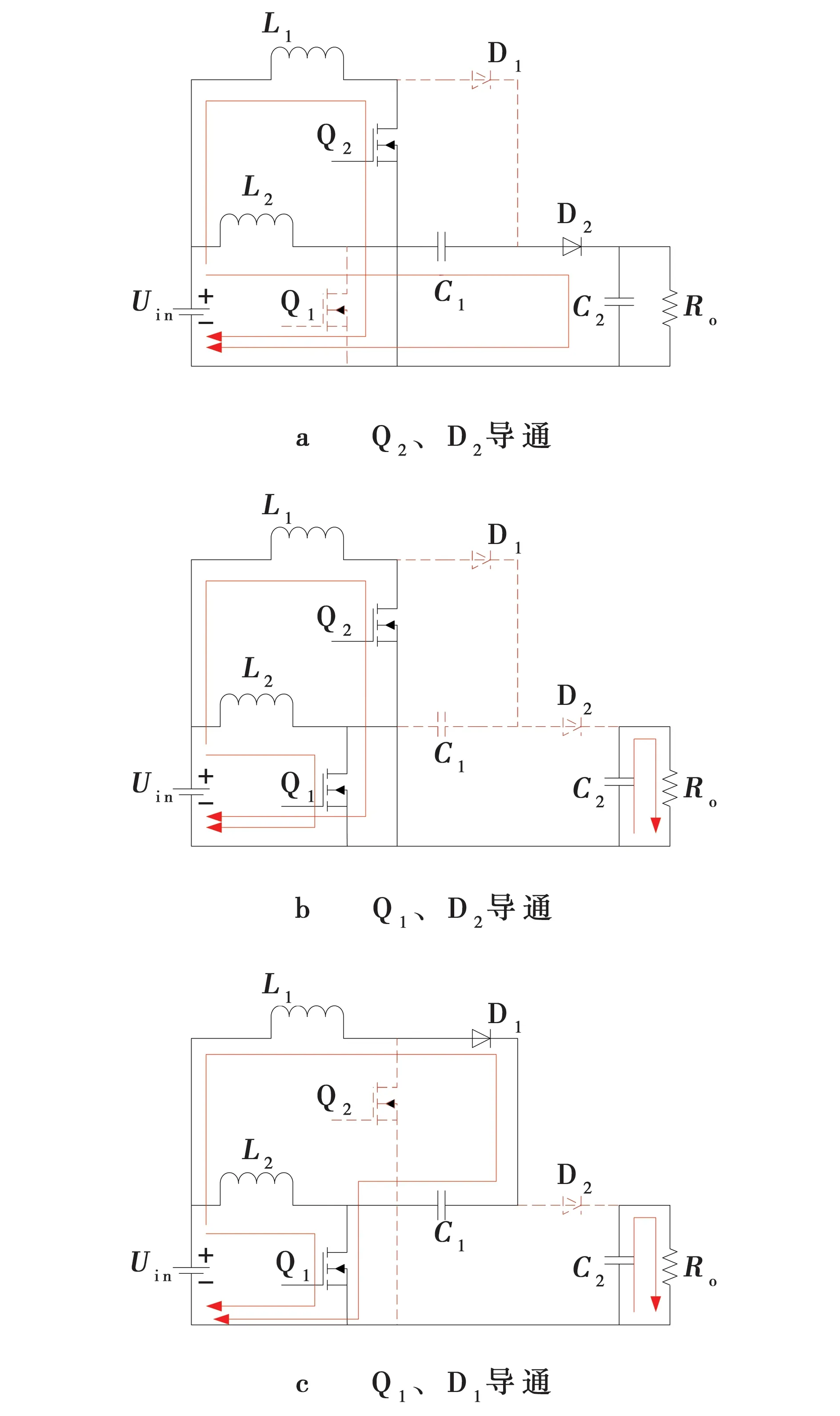
图5 等效电路Fig. 5 Equivalent circuit

由图 5c可见，此时开关管Q1、二极管D1处于导通状态，开关管Q2、二极管D2处于关断状态，电感L2吸收能量，电感L1释放能量，电容C1充电，则有电感电流iL2开始减小，电感电流iL1继续增大，电容电压uC1开始增大，输出电压由电容C2提供，此过程在t3时刻结束[4]。

由图5b可见，此时开关管Q1、Q2同时导通，二极管D1、D2同时关断，电感L1、L2同时吸收能量，输出电压由电容C2提供，则电感电流iL1开始增大，iL2继续增大，电容C1由于未参加电路的充放电过程，所以电容电压保持不变，此过程直到t4时刻结束[4]。

3 电路模型

3.1 建立数学模型

阶段1内Q2、D2导通，电感L1吸收能量，电感L2释放能量，电容C1放电，假设设等效开关周其Ts在阶段的运行时间为(0.5-d′)Ts，其中d′=1-d，则有[8]：

(2)

解式(2)可得,此阶段末的状态量为

(3)

(4)

(5)

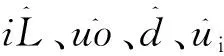
消除后稳态分量后可求得交错并联BOOST变换器从控制到输出的动态数学模型为

(6)

由式(6)可以看出，文中介绍的变换器存在S右半平面的零点。该零点让系统成为非最小相位系统，故在进行控制环节设计需要置PI环节进行补偿，从而消除S右半平面的零点，进而使得系统达到稳定状态[8]。

3.2 电压增益

通过上文的分析，很容易得出电路各个阶段的电路方程。

阶段1

(7)

阶段2和阶段4

(8)

阶段3

(9)

由电感L1、L2的伏秒积平衡以及电容的伏秒积平衡，结合式(7)～(9)可得电压增益M的表达式，以及开关电容C1的电压为

(10)

(11)

3.3 电压应力

由上文分析及图4主要波形可以得出，功率开关管Q1、Q2以及二极管D2的电压应力为

二极管D1的电压应力为

UD1=Uo。

3.4 电感电容参数设计

记电感电流纹波ΔiL，根据图4电感电流的波形图则有

(12)

联合式(10)～(12)整理可得

由于采取的是并联的方式则L1=L1=L/2。记电容电压纹波ΔUC1，根据电容伏秒积平衡原理，有

式中：f——开关频率；

Iin——输入电流[7]。

4 仿 真

为验证方案的正确性，先通过Matlab建立Simulink仿真模型对电路进行仿真验证，电路参数设计如下：输入电压12 V，输出电压60 V，输出功率60 W，电感L1=L2为120 μH，开关电容C1为17 μF，开关频率f取50 kHz。图6是输出电压波形，电压幅值为60 V，与设定的电压值一样。图7、8是满载情况下开关管Q1、Q2及二极管D1、D2的电压应力,其中Q1、Q2、D2电压应力为输出电压的一半，即30 V，D1电压应力为输出电压，即60 V。图9为电容电压波形，其电压值为输出电压的一半，即30 V。

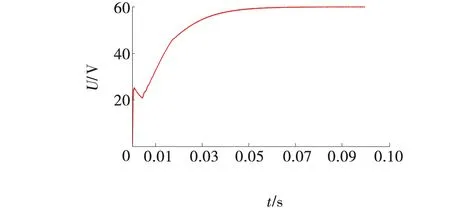
图6 输出电压波形Fig. 6 Output voltage waveform

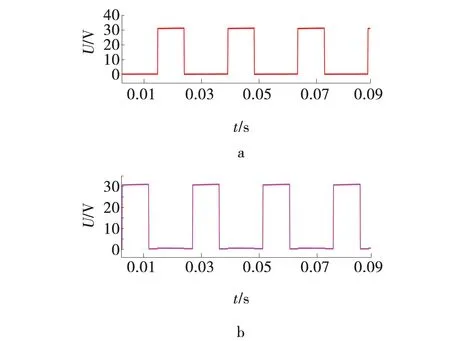
图7 开关管电压应力波形Fig. 7 Voltage stress waveform of mosfet

图8 二极管电压应力波形Fig. 8 Diode voltage stress waveform

图9 C1电容电压波形Fig. 9 C1 capacitor voltage waveform

5 实验数据与分析

为了进一步验证文中所提到的高升压比交错并联DC/DC 变换器的工作原理，在实验室中完成了一个 60 W 的小功率原理样机。实验参数：输入电压Uin=12 V，输出电压Uout=60 V，输出功率Pout=60 W，电感L1=L2=120 μH，采用铁粉芯磁环(外径13.0 mm，厚0.5 mm)，铜线线径为0.7 mm缠绕47圈，开关电容C1=47 μF，开关频率f=50 kHz，输出滤波电容[9]C2=470 μF。图10是PWM输出占空比，D的值为0.6。图11是满载情况下输入、输出电压、输出电压为60 V，输入电压为11 V。图12为二极管D1、D2电压应力波形，从图12可以看出D1的电压应力为输出电压60 V，而D2的电压应力为输出电压一半，由于实际电路存在损耗，因而电路波形与仿真波形有一点差异，图13为开关C1电压波形，其电压只有输出电压一半。图14为开关管电压应力波形，其承受的电压为输出电压的一半，与传统拓扑结构相比，电压应力降低，在进行电路设计具备较强优势。

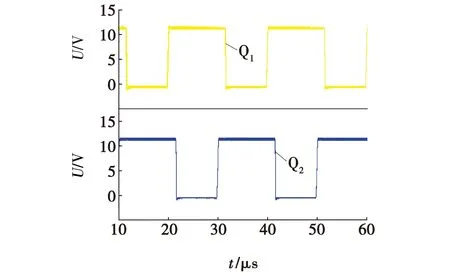
图10 PWM输出占空比Fig. 10 PWM output duty ratio

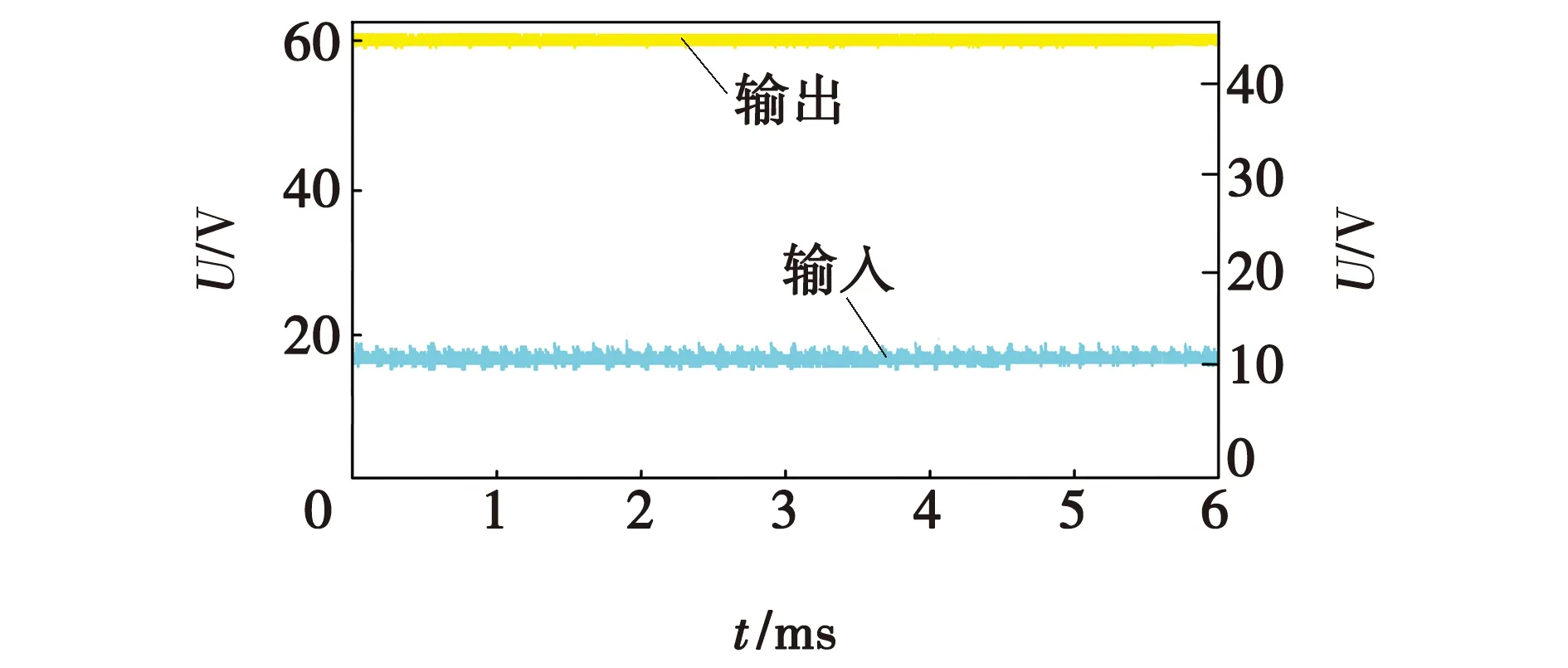
图11 输入、输出电压Fig. 11 Input and output voltages

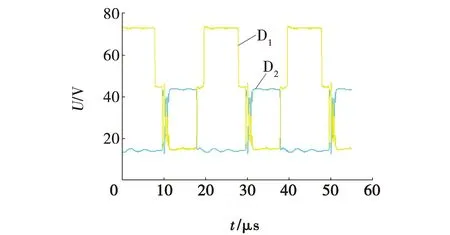
图12 二极管电压应力波形Fig. 12 Diode voltage stress waveform

图13 C1电容电压波形Fig. 13 C1 capacitor voltage waveform

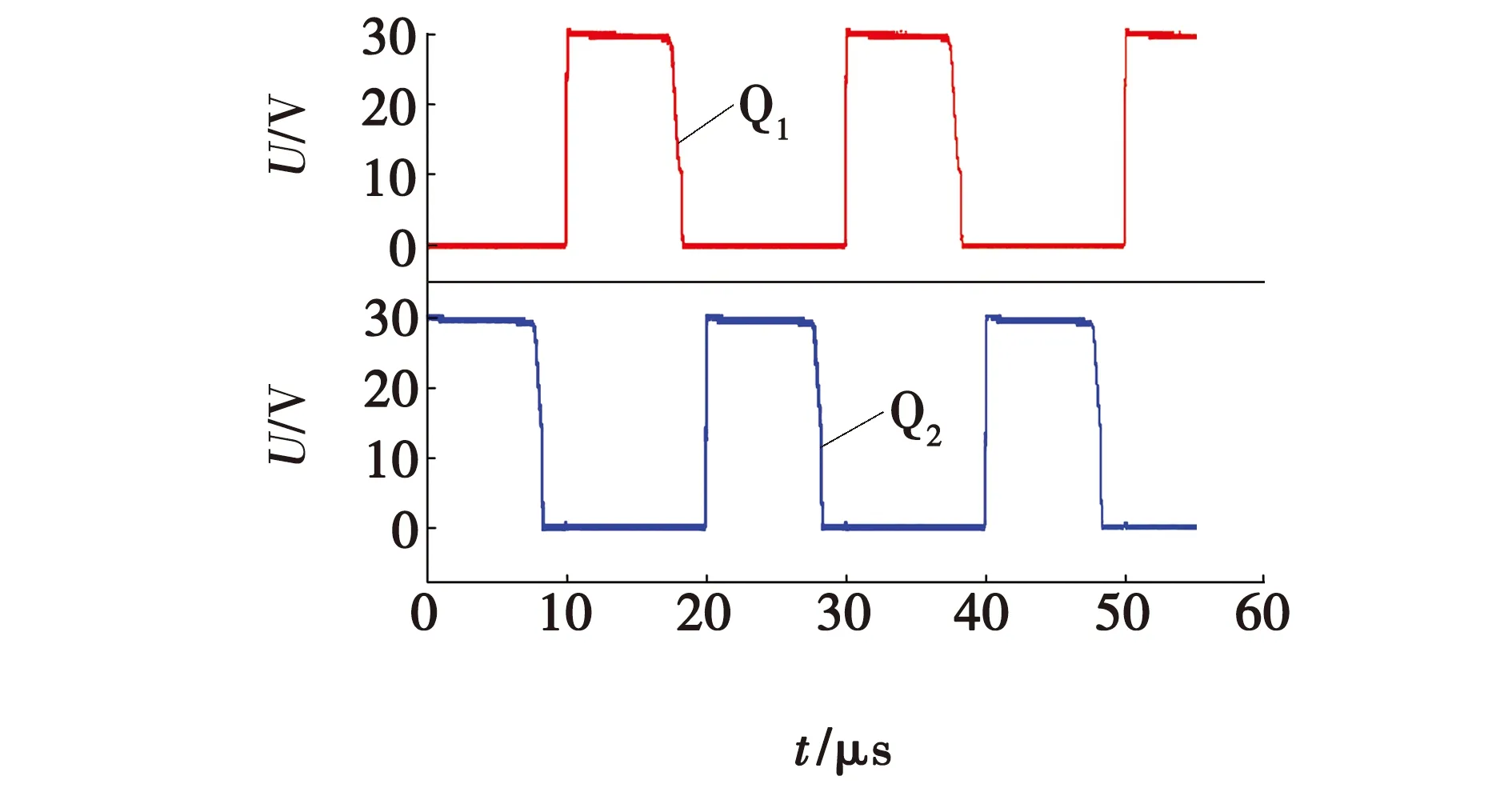
图14 开关管电压应力波形Fig. 14 Voltage stress waveform of mosfet

6 结束语

为实现高增益的电压输出，设计了一款交错并联BOOST变换器，完成了电路的原理分析及仿真电路建模。实验研究表明，该交错并联BOOST变换器不仅使电压增益为传统交错并联结构的两倍、开关管Q1、Q2以及二极管D2的电压应力为输出电压的二分之一，而且电容C1的电压值为输出电压的二分之一。由于在实验过程中未对另一路电路结构进行改进，仍然有一个二极管的电压应力很高，不利于元器件选型，下一步将对电路结构进行优化。