小学数学教学中教师创设情境培养学生转化意识的方法分析

摘 要：在小学数学教学中不仅要让学生获得能够适应社会生活和进一步发展所必需的基础知识、基本技能，还应让学生获得必备的基本思想方法。转化思想是学生连接新旧知识、解决数学问题的必备思想方法，教师在教学过程中要努力创设情境，培养学生的转化意识，使学生养成自主转化的习惯。

关键词：转化;创设情境;解决问题

学生在数学学习中不仅要掌握必备的基础知识和基本技能，更要学会运用数学的眼光和思维解决实际问题。让学生学会根据已有知识，从实际背景中抽象出数学问题，构建数学模型，解决问题是数学学习的关键。

小学数学中转化思想是指把生疏问题转化为熟悉问题，将抽象的问题转化为具体的和直观的问题;将复杂的问题转化为简单的问题，将实际问题转化为数学问题等，从而使问题易于解决。它是数学学习过程中最常用的思想方法，是数学问题解决的基本思路和途径之一。教师数学教学过程中应让学生养成自觉转化的习惯，提高学生解决问题的能力。下面就以“三角形的面积”一课为例，谈谈如何利用转化思想，提高学生解决问题的能力。

一、 挖掘生活资源，转化成数学问题

现实生活中蕴涵着大量与数量和图形有关的问题，教师要引导学生把这些问题抽象成数学问题，用数学的方法加以解决。在这过程中，就需要引导学生树立敏锐的数学应用意识，主动把现实生活中的问题转化成数学问题，进行探究，以找到解决问题的突破口。

环节一：谈话中引入

成为一名少先队员后，我们每个人都要佩戴红领巾。红领巾是什么形状的，如果要想知道它用多少面料，要怎样解决呢？

从学生熟知的红领巾入手，让孩子对知识产生亲切感，顺利引领大家把现实问题转化成数学问题，找到解决实际问题的突破口，从而顺利转入新知的学习。

二、 联系已有知识，转化成数学猜想

在学习“三角形面积”之前，学生已经掌握了平行四边形面积的推导方法，也就是说学生已经积累了把未知图形面积转化成已知图形面积的一种方法，并且理解了其中的数学思考方法。当学生遇到求三角形面积时，就能根据已有知识进行合理猜测。

环节二：追问促猜想

追问：怎样求三角形的面积？

你能回忆一下平行四边形公式的推导过程吗？

大胆猜测一下，可以把三角形转化成我们已经学过的哪些图形？

（可以把三角形转化成长方形，可以把三角形转化成正方形，可以把三角形转化成平行四边形？）

通过回忆唤醒学生已有知识，引导学生大胆猜测，让孩子养成碰到问题能主动联系已有知识进行大胆猜测，然后进行实践验证的习惯。

三、 参与实际操作，转化中解决问题

学生知识的获得不能依赖死记硬背，而应以理解为基础，让学生主动参与实践操作，把思维和行动融合在一起，

这样才能不断地验证自己的猜想，找到最佳的问题解决策略，为今后解决实际问题奠定基础。

环节三：小组合作促转化

1. 材料包

钝角三角形、锐角三角形、普通直角三角形、等腰直角三角形各4个，剪刀、直尺等。

2. 思考

计划把三角形转化成哪个猜想的图形？在转化过程中用了几个三角形？

如果是一个三角形，你们怎么转化，如果是两个又怎么转化？……转化后图形与原三角形又有什么关系？

3. 操作过程中，填好相应的学习单

我们是用（  ）个（  ）三角形，通过（  ）转化成了一个（  ）。

原三角形的底等于转化后（  ）形的（  ）;原三角形的高等于转化后（  ）形的（  ）;原三角形的面积等于转化后（  ）形的（  ）。

教师要给予充足的材料，让学生有更多的探索空间，让他们在合作中主动参与、提出各自解决方法，并在与他人的交流合作中选择合适的策略，丰富数学活动的经验，碰撞出思维的火花，提高思维水平。

环节四：转化图形的呈现

教师给学生充足的表达空间，培养他们的语言表达能力、倾听能力、辨思能力，让其找到别人解决问题的关键之处，也让孩子们发现更多解决的方法，以拓宽自己的思维。

转化类型倍拼法割补法折叠法

正方形

长方形

平行四边形

发现：平行四边形通过沿高剪切，然后平移可以转化成长方形，但由于三角形在分割的時候无法沿用平行四边形的剪切方法，因此大部分组都采用的是倍拼法，割补法只有少数组运用。

没有学生应用折叠法，老师可以展示这一方法，为他们的思维开拓一条新路。

割补法和折叠法的展示激发了孩子们探究的兴趣，引发了学生自主操作，提高了学生的推理能力。思维的发展是一个不断递进的过程，只有当孩子在经历长期的不断反思、不断质疑、不断改进中才能得到逐步的提升。

环节五：对应量的转化

根据转化图形推导出三角形面积公式。

在解决问题的过程中，我们要在粗犷的线条中，寻找细腻的支点，从而找准图形对应量之间的关系，准确推导出三角形的面积公式，这是学生知其所以然的关键，也是学生获得最终成功喜悦的关键。

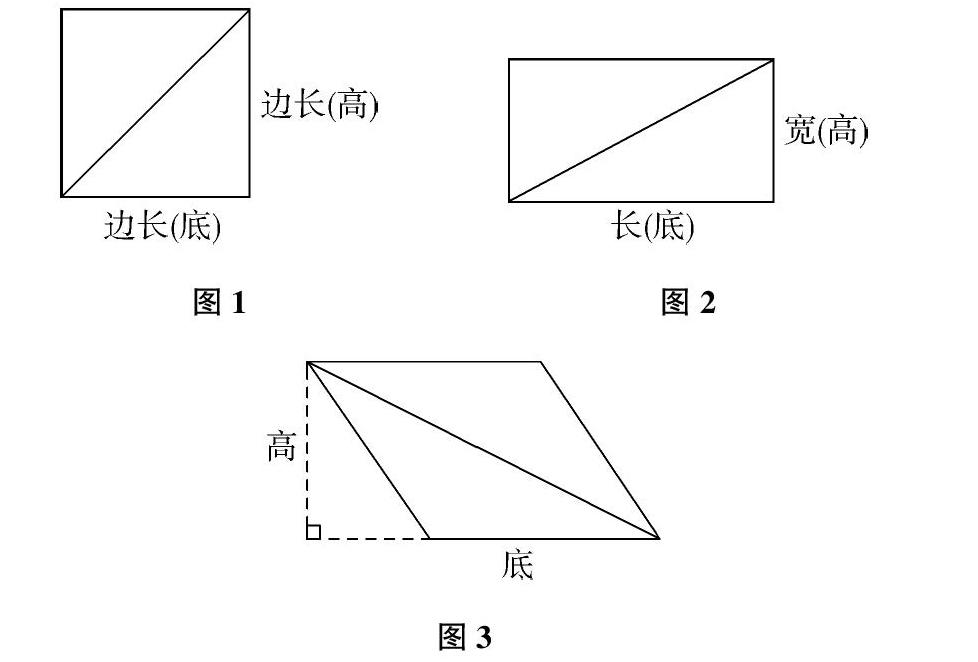
图1拼成的正方形的边长等于原三角形的底，边长等于原三角形的高。

图2拼成的长方形的长等于原三角形的底，宽等于原三角形的高。

图3拼成的平行四边形的底等于原三角形的底，高等于原三角形的高。

所以推导出三角形的面积=底×高÷2

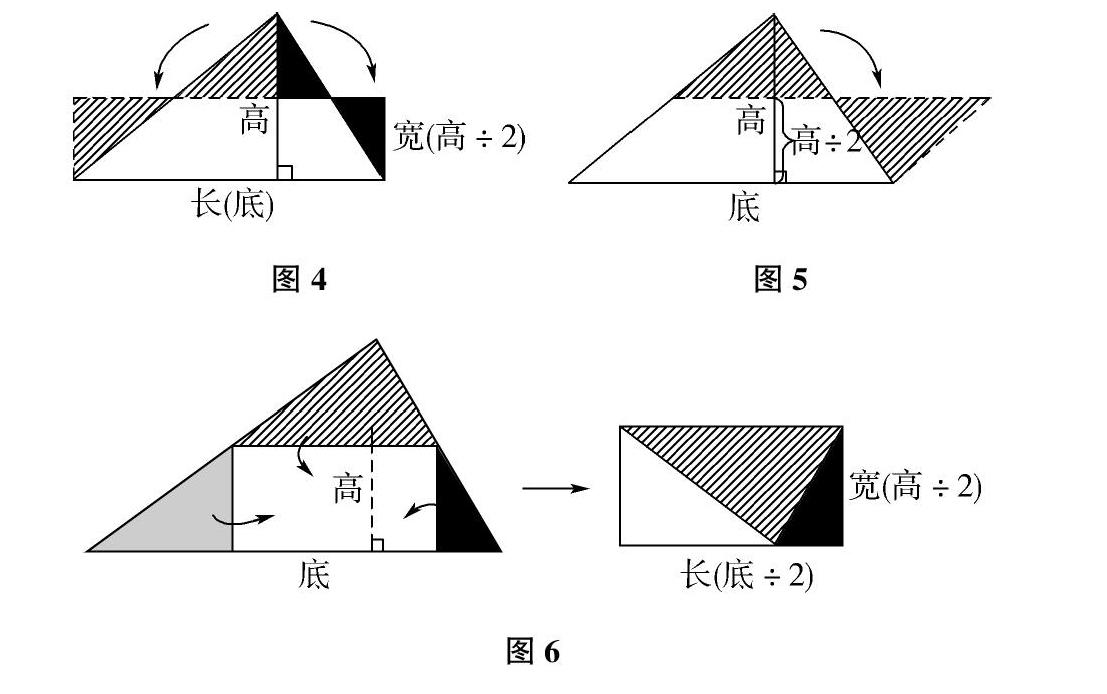
图4拼成的长方形的长等于原三角形的底，宽等于原三角形高的一半。

图5拼成的平行四边形的底等于原三角形的底，高等于原三角形的高的一半。

由图4图5可以得出：三角形的面积=底×（高÷2）

推导出：三角形的面积=底×高÷2

图6折出的长方形面积是三角形面积的一半，长和宽也分别是三角形底和高的一半。

三角形的面积=（底÷2）×（高÷2）×2

推导出：三角形的面积=底×高÷2

用字母表示S=ah÷2

教学是一个循序渐进的过程，教师不仅要让学生掌握结果呈现的知识，更应重视学生思维的形成过程，这样才能提高学生的探究意识、应用意识和创新意识。在上面的转化推导过程中，使学生知道了结果，也感悟了结果产生的原因。

四、 对比今古思维，感受转化魅力

在悠久灿烂的中国古代文化中，数学文化是其中一朵绚丽的奇葩，它是古代科学的基石，是中华文化不可缺少的一部分，其充分展示了古代劳动人民的聪明才智。在两千多年前人们就熟练掌握了转化的方法，并将其用之于实际生活中，为人类社会生活以及社会进步做出了重要的贡献。转化思想在人类历史长河中，在各个方面的发展中都起着重要的作用。

环节六：阅读中感悟

现在我们通过几种方法推导出了三角形的面积公式，你们知道古代人们是怎样计算三角形面积的吗？

在阅读中让学生产生思维的碰撞，感受古代劳动人民的伟大，感受古今方法的相通之处，知识的转化是解决问题的关键，教师要让他们发现我们在前人的基础上开拓了新思路，有了新方法。

五、 比较不同转化，找到最佳策略

我们在追求思维广度和方法多样化的同时，也要让学生在比较中感受方法的简单化。

环节七：质疑中强化

追问：1. 我们可以用这么多种方法推导出三角形的面积公式，为什么书本上只用了“倍拼法”？

2. “倍拼法”中三角形和所拼成的平行四邊形什么关系？

引导得出：三角形的面积等于等底等高平行四边形面积的一半。强化“等底等高”，加深学生对三角形面积公式中“÷2”的理解。

通过运用上面三种不同方法推导得出公式，学生自然发现“倍拼法”得出的三角形面积公式最为简单。简单化是数学最基本、最显著的一个特征和方法。数学学习追求思维的简单，形式的简单，解决问题的简单。为什么我们要推导出三角形的面积公式呢？这是因为数学不仅要追求简单化，也要追求统一性，建立数学模型，使大家能用最简洁的方法解决三角形的面积问题。在三角形的面积计算时“÷2”是学生最容易遗漏之处，教学时，教师不仅要让孩子们在数形结合中理解“÷2”的意义，也要反复强调，多次练习巩固。

六、 利用新知，解决实际问题

环节八：巩固促转化

获取知识最终是要去解决相应问题的，只有这样才能体现学习的价值，在通过转化推导得到三角形的面积公式后，教师应让学生把所学的知识再应用到实际问题中，激发学生的学习热情，让其感受成功的喜悦，提高学习数学的积极性。同时在解决实际问题的过程中，要引导学生进一步巩固所学的知识，为下一次知识的转化做好准备。

1. 小组测量红领巾底和高，求红领巾面积

测量过程中感受三角形的底和高必须相对应，感受探索成功的喜悦，激发学生学习的积极性。

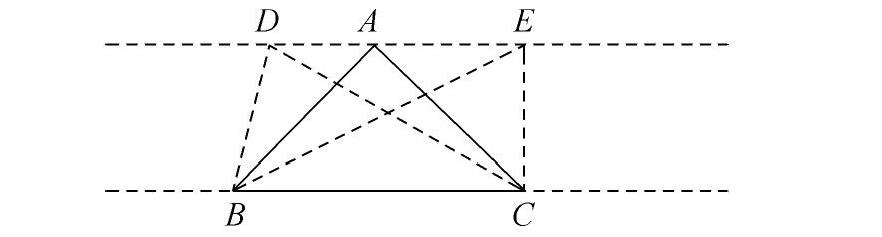
2. 下图中哪个三角形面积与三角形ABC面积相等，为什么？

在题2的解决过程中，又一次实现了知识的完美转化，让学生明白三角形的面积大小不受形状的影响，只与三角形的底和高有关，得出“等底等高三角形的面积相等”的结论。

教学是一个逐步完善的过程，学生的学习也是一个逐步进步，缓慢上升的过程。教师要努力在教学中为学生创设教学情境，激发他们的学习热情，使他们全身心地投入教师精心组织的教学活动中，这样学生才能在数学思考、问题解决和情感态度等方面得到发展。

参考文献：

[1]义务教育数学课程标准（2011年版）[S].中华人民共和国教育部，2012（6）.

[2]刘超.从冲突质疑走向深入思考[J].小数数学教师，2021（6）.

[3]吉智深.在比较和对比中培养学生发现问题并提出问题的能力[J].小学数学教师，2020（4）.

[4]李惠玲.以“问题串”为主线，凸显知识本质[J].中小学数学，2021（1）.

作者简介：汤金红，浙江省杭州市，浙江省杭州市萧山区高桥小学。