基于鲁棒性随机分割森林算法的变压器损耗异常值检测

张国芳 温丽丽 吴蒙 刘通宇 郑宽昀 黄福兴 袁培森

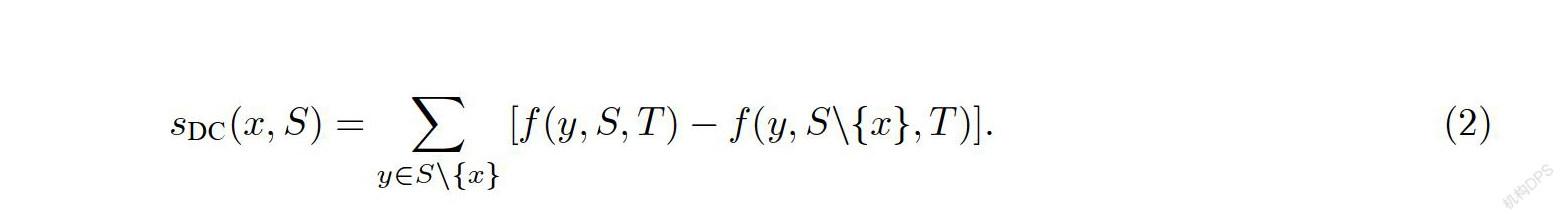
摘要：在智能电网飞速发展的趋势下，新型数字基础设施建设成为电力企业的核心业务之一，电力企业数据的治理和智能化分析为平台运营、数据增值变现等商业模式创新提供了条件.在电力数字化和智能化治理背景下，使用鲁棒性随机分割森林算法实现变压器损耗数据的异常值智能化检测.通过鲁棒性随机分割森林算法划分样本点以构建鲁棒性随机分割森林结构模型，通过插入和删除样本点对结构复杂度的影响程度给定该样本点的异常值评分.鲁棒性随机分割森林算法适用于实时损耗数据异常检测，兼顾异常值检测效果和运行效率，具有较高的可信度.对真实变压器损耗数据集中进行异常值检测试验，实验结果表明该算法高效、灵活，相较于其他方法，精确率、召回率及运行效率均有显著提升.

关键词：鲁棒性随机分割森林;异常值检测;变压器损耗;电力数据中台

中图分类号：TP391文献标志码：ADOI：10.3969/j.issn.1000-5641.2021.06.014

Anomaly detection of transformer loss data based on a robust random cut forest

ZHANG Guofang1，WEN Lili1，WU Meng1，LIU Tongyu2，ZHENG Kuanyun3，HUANG Fuxing3，YUAN Peisen2

（1. State Grid Sichuan Electric Power Company，Chengdu 610094，China;2. College of Artificial Intelligence，Nanjing Agricultural University，Nanjing 210095，China;3. Nanjing Automatic Research Insititute Group Corporation （State Grid Electric Power Research Institute），Nanjing 211106. China）

Abstract：With the rapid development of smart grids，the construction of new digital infrastructure has become one of the core businesses of power companies. Power companies' governance and intelligent analytical capabilities enable opportunities for business model innovation，such as platform operation and value-added data realization. In the context of power digitization and intelligent governance，we use the robust random cut forest in this paper for transformer loss data anomaly intelligence detection. The algorithm divides sample points by random cutting to construct a random cut forest structure model by inserting and removing sample points in the structure;the anomaly score of a sample point is then given by the influence of complexity. This method is suitable for anomaly detection on real-time loss data and offers a high degree of credibility，effectiveness，and efficiency. An experiment of anomaly detection on real transformer loss data shows that the method is efficient and flexible. The accuracy，recall，and efficiency of the proposed method，moreover，is substantially better than alternatives.

Keywords：robust random cut forest;anomaly detection;transformer loss;power data platform

0引言

近年來，电网正在朝着信息化、数字化和智能化方向迅速发展[1].在能源互联网发展背景下，电力企业数值化和智能化转型是突破业务发展瓶颈的关键.需要提升电网系统数据的采集实时性、治理科学性，提升电网运行数据的综合治理能力与智能化管理水平.

构建一个统一的、可复用的电力企业数据中台[2]，以形成将数据变成资产并服务于业务的机制，这是电网提升智能化的重要手段[3].为了实现以中台赋能为核心，进而提升电力企业数据处理和服务能力，需要对海量的电能量数据进行统一采集、计算、标准化以及异常值的实时监测.

电能损耗作为电力企业经济效益的重要指标，其管理和分析数据是电力企业数据中台的重要业务.各地区在损耗效益和损耗率水平上也存在一定的差异[4]，如何检测这些电能数据中的异常值以降低电能损耗，是当前国内外研究的一个重点[5-6].其中，在整体线路损耗中，变压器损耗是一个重要的组成部分，利用大数据和人工智能技术展开设备性能评估，对变压器损耗电气设备性能进行评价和分析，可以抓住元件性能老化渐进的量变过程，观察正常运行元件的性能劣化趋势.因此对变压器损耗的异常值检测是构建电力企业数据中台必须考虑的问题[7].

异常值检测（anomalies detection）是数据挖掘中的核心和基础问题[8-9].在电能数据的分析中，由于电能量采集设备故障或者其他人为原因，会导致所采集到的电能量数据产生异常.对于所采集到的变压器损耗数据，通过异常值检测发现异常样本点，有助于发现异常的用电行为和设备故障情况，对提高电能利用效率和降低线路损耗具有指导意义.

在电能量数据异常检测中，常用的异常值检测方法主要可以分为3类：基于统计学原理、基于聚类和基于无监督学习[10-11].基于统计学原理的电能量数据异常值检测方法实质上是基于对样本集的描述统计，以确定一个正常样本数据范围，对于不在这个范围内的样本数据视为异常.

基于聚类的异常值检测以基于DBSCAN聚类的异常值检测为代表，其算法的基本原理是根据样本数据的紧密程度进行聚类划分，选出其中的不能被划分到任何一个聚类簇的样本点作为异常样本点[12].王文红等[13]运用该方法对电能表数据进行异常值检测，结果表明该方法适应性强，它可以充分考虑样本点距离的分布情况，有着较好的异常值检测效果.但是在电能量数据中经常存在高维数据，如果其中一个样本的某一维度的分量出现了异常，在计算距离的时候这样的异常在数值上的体现就会被稀释，另外聚类算法的输入参数会对聚类结果产生很大的影响，选择参数是一个困难的问题.

基于无监督学习的孤立森林算法[14]是一种适用于连续数据的异常值检测方法，如余翔等[15]基于孤立森林算法对用电数据异常进行了研究，发现相较于基于聚类的算法其异常值检测准确率和效率均有所提高.孤立森林算法针对高维数据有着较好的鲁棒性，对每一个样本的异常度提供归一量化指标，但是并没有对电能数据的实时异常值检测进行建模.

上述异常值检测方法是对静态电能量数据集的批量检测，然而对电能量数据的异常值检测问题提出了新的要求：既要考虑数据前后的相关性，又需要考虑如何对于实时发生的电能量数据进行异常值检测.

鲁棒性随机分割森林（Robust Random Cut Forest，RRCF）算法是一种面向动态数据流的异常值检测算法[16]，该算法针对持续产生的数据，考虑到样本点数据时间这算法一维度.该算法基于孤立森林结构，优化了随机分割树的生成算法，改进成为鲁棒性随机分割树（Robust Random Cut Tree，RRCT），并提出了基于模型复杂度的异常评分.RRCF算法能通过一次遍历样本集获得每个样本点的异常评分，有着较为理想的运行速度.RRCF算法在诸多领域已经有初步应用，例如，Inoue等[17]将RRCF算法应用于水质异常的实时监测，Bartos等[18]则将该算法应用于城市交通的实时车流量监控，Wang等[19]将该算法应用于大型互联网公司系统的各种关键性能指标分析.上述应用均取得了较好的效果，证实了RRCF算法在异常值检测方面的优势.

本文提出了基于RRCF算法的变压器损耗数据异常值检测方法，构建了对于变压器损耗数据流的实时异常值检测模型.本文采用了南瑞集团提供的2017—2020年变压器损耗数据，经过预处理后利用该数据集构建RRCF模型以计算异常评分，对变压器损耗数据进行异常值检测，作为评估变压器性能的重要参考依据.

1变压器损耗数据的异常值

变压器在运行时，绕组内通过电流，会产生负载损耗，还会产生一些附加损耗，主要有绕组涡流损耗、环流损耗和杂散损耗.其中负载损耗的计算公式为

其中，I，I分别是原副绕组额定相电流，单位为A;r，r分别是折合为75℃时原副边绕组的总电阻，单位为Ω.

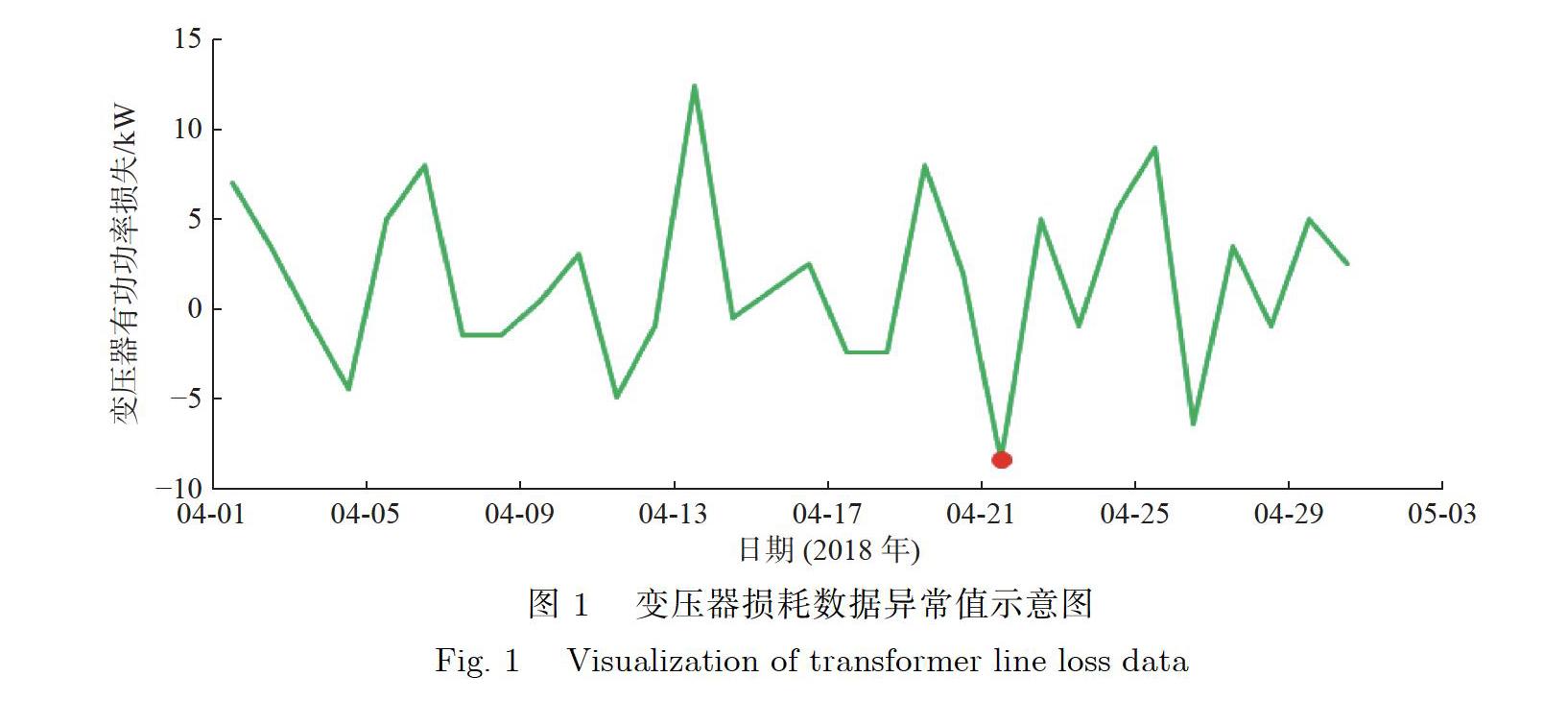
变压器损耗数据具有很强的时间相关性，是时间序列数据[20]，需要对该变压器损耗数据集设计一种高效的，对于实时生成的变压器损耗数据进行异常值检测的算法.异常样本是某个样本集中存在但是与其他样本点特征存在显著差异的样本点，又称离群点[21].当在某一时刻发生突变时，该数据点有较大的可能代表异常样本.图1展示了某地变压器损耗的变化情况，可以发现在2018年4月下旬，变压器损耗数据发生突变，损耗数值突然降低，说明该样本点很有可能是异常样本点，该数值很可能是变压器损耗数据中的异常值，需要对该样本点做进一步的异常分析.

2基于RRCF算法的变压器损耗異常值检测

2.1模型架构

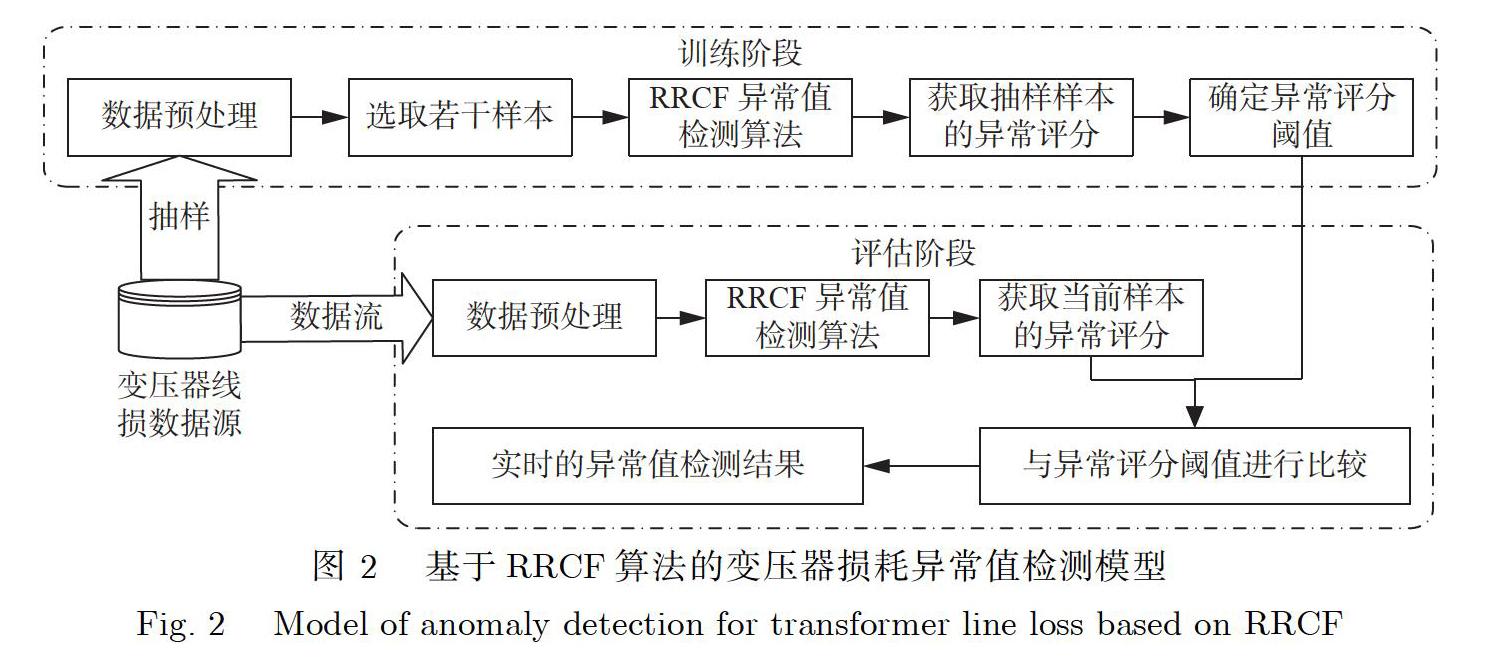
对于变压器损耗异常检测这一问题，提出基于RRCF算法的变压器损耗异常值检测方法，使用基于RRCF算法的异常值检测方法进行异常值检测的整体流程.其流程主要涵盖训练阶段和评估阶段，检测模型如图2所示.

A.训练阶段

第1步：收集不同时间节点不同地区的变压器运行检测参数，以此计算变压器损耗，得到变压器损耗原始数据集.

第2步：确定线路损耗数据的地点、时间范围，从数据库读取相应样本数据并进行预处理，预处理的过程如下：

①检查每个样本信息，若样本属性值缺失则剔除该样本;

②对每个样本的变压器损耗数据字段取绝对值;

③依据样本损耗数据的采集时间，将样本损耗数据整理成时间序列数据，将样本数据的采集时间作为索引方便后续算法的快速查找定位.

第3步：设定RRCF异常值检测算法的参数，对预处理后的时间序列数据进行异常值检测，获得每一个样本点的异常评分.

第4步：对样本点的异常评分进行阈值检验，确定针对变压器损耗异常值的异常评分阈值，根据此阈值筛选得到异常样本点的信息.

B.评估阶段

第5步：根据第4步得到的异常评分阈值，建立对于实时变压器损耗数据流的RRCF异常值检测模型，该模型主要包括RRCF结构和异常评分阈值两个部分，均通过训练阶段确定.

第6步：对数据流中的每一个数据依据第2步的方法进行预处理，包括去除缺失样本和绝对值化处理.

第7步：依据RRCF模型对每一个样本计算异常评分，并与异常评分阈值进行比较，实时输出异常值检测结果.

2.2基于RRCF算法的变压器损耗异常检测的实现

2.2.1RRCF算法和异常评分

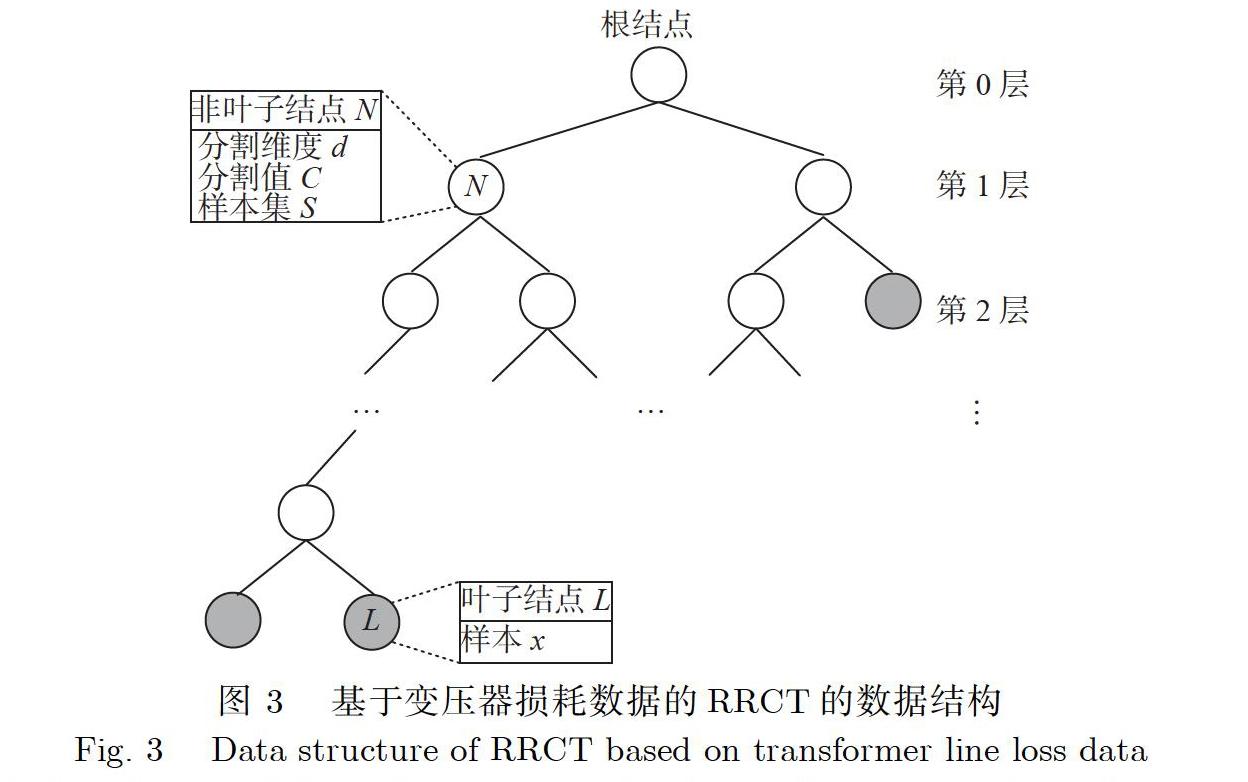
RRCF算法进行异常值检测的基本原理是维护一个时间序列数据滑动窗口生成的二叉树结构，称为鲁棒性随机分割树，它的每一个叶子结点都是样本点，非叶子结点是其左右子结点的样本集合，根结点是原始数据集合.下面给出基于变压器损耗的RRCT的定义.

定义1基于变压器损耗的RRCT要么是一棵空树，要么是一棵具有如下性质的二叉树：

●所有结点对应一个变压器损耗样本集，根结点包含全部变压器损耗样本集.

●非叶子结点除了对应一个样本集，还需要指定分割参考维度d和分割值C.

●若左子树不空，则左子树根结点包含的样本集的第d维数据均小于等于C，d和C的值由根结点决定.

●若右子树不空，则右子树根结点包含的样本集的第d维数据均小于C，d和C的值由根结点决定.

●左右子树也分别为RRCT.

RRCT的数据结构示意图如图3所示，图3还表明了RRCT中叶子结点和非叶子结点存储信息.

对于一个包含有n个样本的初始变压器损耗样本集，首先选取前k个样本点作为初始化样本点，以此初始化RRCT，此时RRCT是一棵包含k个叶子结点的二叉树.通过递归方式生成RRCT，具体如算法1.

算法1的处理过程如下.

1）算法1的第3行指出了递归截止的条件，目的是保证叶子结点仅有一个样本点而非叶子结点包含数个样本点.

2）算法1的第7行和第8行是体现随机分割形成二叉树的步骤，对于随机分割，一方面要选择使用哪一个维度的样本数值进行分割，即d值的选择;另一方面要在选定维度后将样本点分成两个部分的分割值，即。值的选择.对于d值的选择，每一个d值被选中的概率是和当前样本集d维度数据的极差/成正比的，即同一纬度的样本集数据的一个维度最大值和最小值之差越大，则该维度被选中的概率就越大;对于。值的选择，则是服从当前样本集被选中维度的最小值和最大值的均匀分布.

3）算法1的第9行和第10行，将S分割成S和S两个部分，分别成为该结点的左右子树.算法的第11—12行，在左右子树中继续完成分割，进而递归地向下生成RRCT.

通过上述方式生成的RRCT，对于一个样本点对应的叶子结点，将其插入RRCT，如果它再经过数次的随机分割就能将该样本与其他样本分割开来，说明这个点与RRCT中其他样本点有着显著的差异，很有可能是异常点.

对于RRCT的复杂度可以用所有叶子结点深度之和来进行衡量.由于RRCF算法对于异常样本点的定义为如果该样本点加入RRCT会显著增大RRCT的复杂度则认定该样本点为异常样本点.下面给出异常评分的定义.

定义2设样本点x∈S，样本集S生成的RRCT T，x获得的异常评分s计算方式如式（2）所示：

其中，函数f是对于样本集S生成的T中任意一个叶子结点y的深度.由式（2）可知样本x异常评分s的实际意义是当样本点x被移除时，RRCT树T中所有叶子结点深度之和的变化值.异常评分越接近于0，样本点是异常样本点的可能性越小.

2.2.2样本点的插入和删除

RRCF异常值检测方法最重要的部分就是对RRCT结构的维护，使之包含恒定数量的样本点，因此在RRCT中删除和插入样本点的操作是必要的.从RRCT中删除一个样本点的算法如下所示.

考虑到RRCT的性質，删除的一定是一个叶子结点，因此删除样本点的操作可以得到简化.其做法是找到欲删除样本所对应的叶子结点，找出其兄弟结点，用兄弟结点代替其父亲结点并直接删去欲删除的叶子结点.

在RRCT中插入一个样本点的算法如下.

1）算法3是假设这个样本点已经被加入样本集合S中，进行一次随机分割得到新分割值根据计算新分割值的结果分别处理：

a）如果这个随机分割值是符合原样本集S进行的分割（这个分割值不超过原样本集该维度数据的上下界），那么就递归地往该结点的左或右（取决于样本该维度数值与原分割值的比较结果），继续向下寻找一个合适的结点进行插入.

b）如果这个随机分割值不符合原样本集S进行的分割，则生成一个新结点替代该结点，原来该结点的子树和样本点对应的叶子结点分别成为该新结点的左右子树（左右子树取决于样本该维度数值与新分割值的比较结果）.

2）算法3的第2行指出了递归寻找插入点的终止条件.

3）算法3的第5—9行指出了计算新分割值C′的方法，这样做是为了维持RRCT随机分割的特性，与算法1中获得k值和C值的方法相对应.

4）算法的第10—17行进行的操作对应了情况a）的处理，算法的第18—23行对应情况b）的处理.

2.2.3变压器损耗异常的实时检测

基于上述异常评分的计算方法，在一个样本点加入RRCT中，根据RRCT的结构为该样本点生成异常评分.考虑为变压器损耗异常值检测实际问题，设定一个异常评分阈值，如果新样本点对应的异常评分超过了这个阈值，则可以立刻反馈异常值检测结果.

有关异常评分阈值的确定，是根据所有样本点赋予的异常评分降序排列，取前2%的样本作为异常样本点，以确定正常样本点和异常样本点的临界值，并将该临界值作为异常评分的阈值.

综合算法1—3，给出基于RRCF算法的变压器损耗异常值检测方法的完整描述，具体如下.

该算法的总体流程归纳如下：

1）选取前k个样本点以初始化RRCT（第1步）.

2）从第k+1个样本点开始，以先入先出队列的方式替换RRCT中的样本点，在删除最旧样本点的同时计算其异常评分并记录（第2—5步）.

3）以异常评分s降序排列第1到n-k个样本点（第6步）.

4）输出前2%的样本点，认定这些样本点为异常样本点（第7步）.

3实验及结果分析

3.1测试环境

实验环境：处理器Intel Core i5-8265U 1.6 GHz，内存8.00 GB，硬盘1 TB;操作系统Windows 10，Python 3.6和sklearn 1.91.

3.2数据集及预处理

数据采用南瑞集团提供的2017-09-01到2020-03-30的变压器损耗数据，原始数据的字段包括记录时间time、线损率rate、线损值value、正向有功总电量PAP和反向有功总电量RAP.

预处理操作包括将字段value缺失的样本点删去，标准化time的格式并升序排列;将value和rate取绝对值，对于超出均值正负3个标准差的样本，认定为无效数据，将这些样本点删去.原始数据的样本个数为1378，预处理后样本个数为942.

3.3评价指标

异常值检测效果主要通过准确率（accuracy），精确率（precision），召回率（recall）以及综合评价指标F值（F-measure），这4个指标进行评价[21]，设准确率为A，精确率为P，召回率为R和F值为F，如式（3）—（6）所示.

其中，n，n，n，n分別表示异常点检测为异常，正常点检测为正常，正常点检测为异常，异常点检测为正常的样本点个数.

3.4实验结果

3.4.1样本点个数k与异常评分

对于基于RRCF算法的变压器损耗异常值检测算法，初始化样本点个数k是一个与检测结果密切相关的参数，因此有必要研究参数k对异常值检测效果的影响.

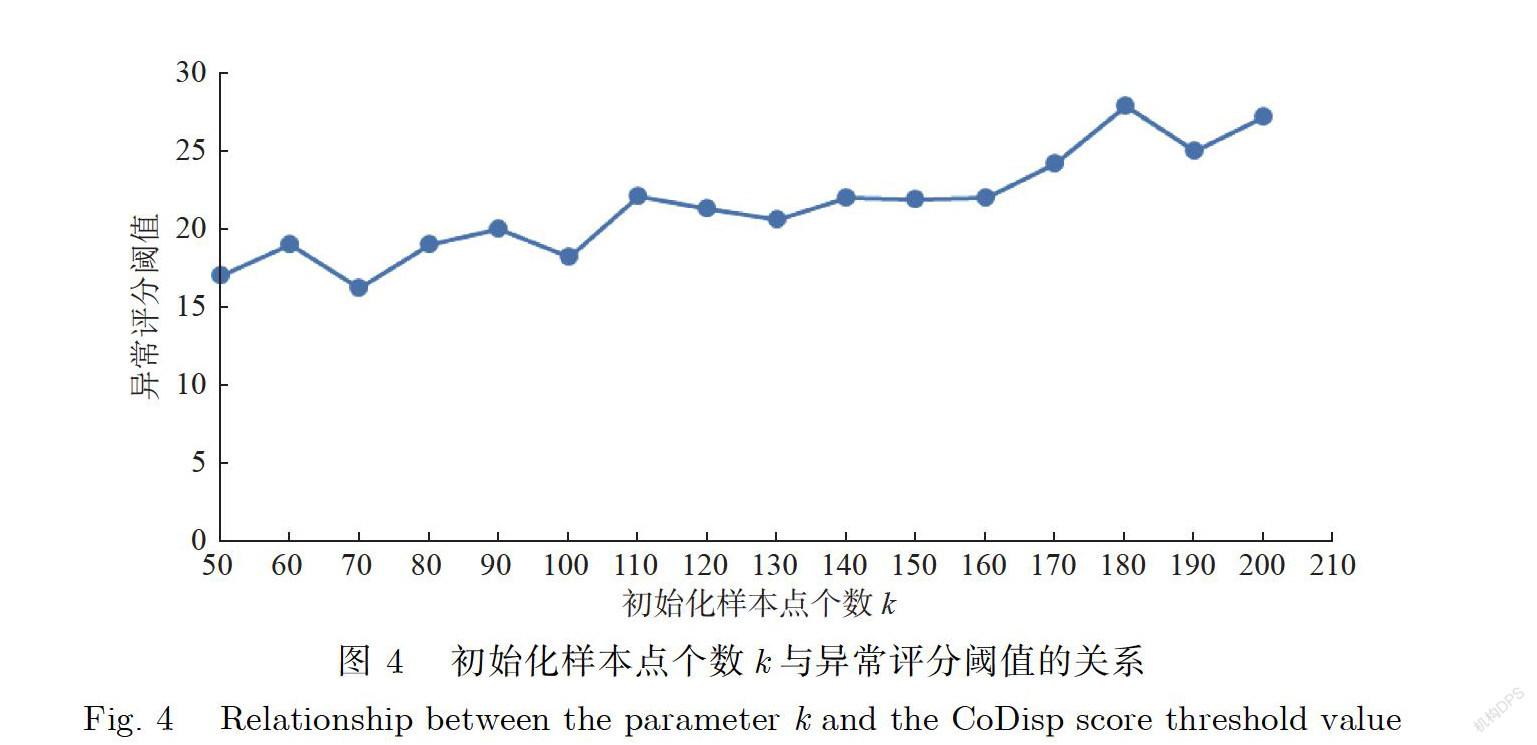
首先研究参数k在不同取值下，运行算法4得到的异常评分阈值与参数k之间的关系.在实验中，令参数k的取值范围为50到200，步长为10，参数k的取值共16种.考虑到随机分割森林的特性，每种参数k的取值，基于变压器损耗时间序列数据进行10次重复实验并取得平均值，得到的结果如图4所示.

由图4可知，对于一个确定的时间序列数据，得到的异常评分阈值有一定上下波动，但初始化样本点个数k近似呈现正相关的关系.这一点和前文异常评分的定义是一致的，也与RRCF算法随机分割的性质对应.参数k决定了RRCT模型的规模（包含的样本点个数），随着RRCT模型规模的增大，当样本点加入模型之后导致的平均叶子结点深度变化也会增大，进而导致异常评分的整体提高.

3.4.2样本点个数k与F值

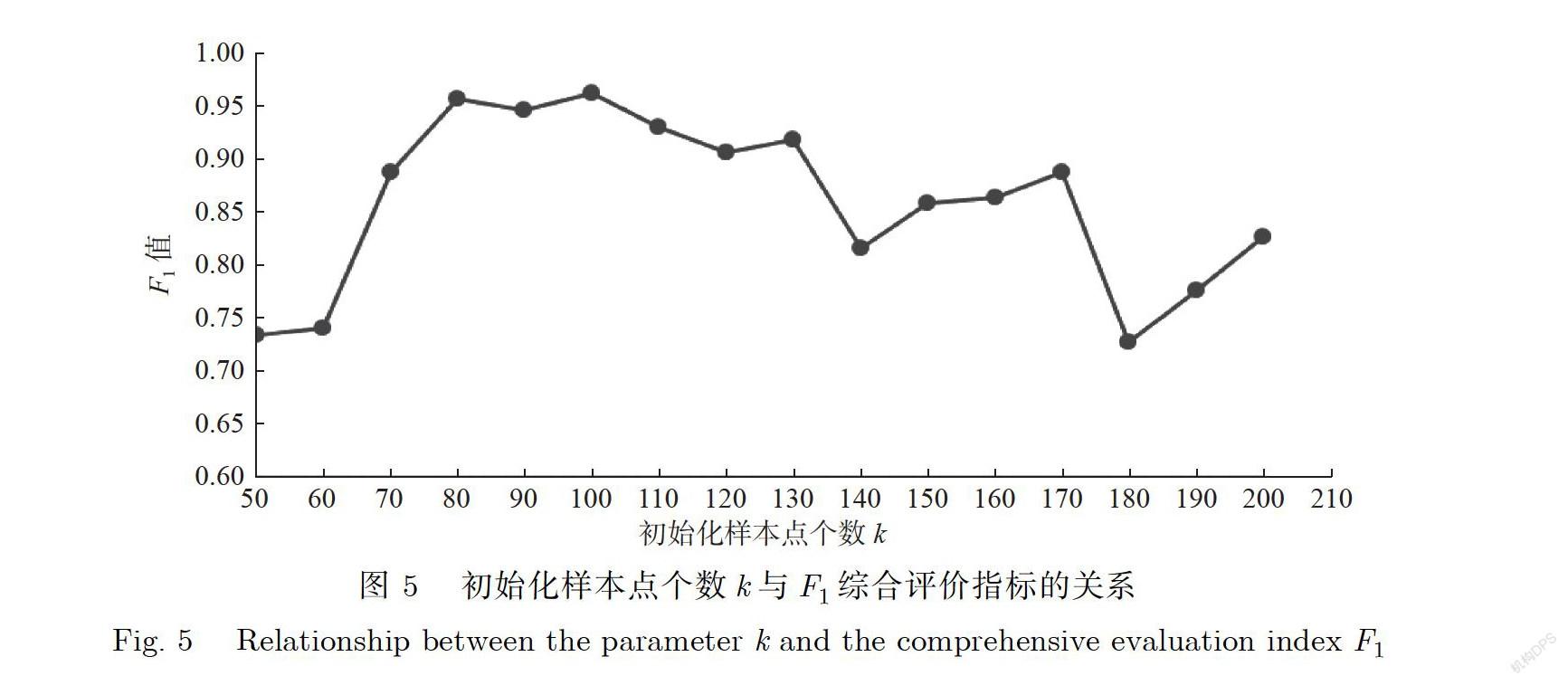
基于随机分割树的随机分割的性质，又考虑到变压器损耗数据中异常样本点数量占总样本点数量较小，精确率和召回率对评价针对该数据集的异常值检测比较具有参考价值，因此选取综合了精确率和召回率的评价指标F值作为异常值检测的评价标准.对于每一个参数k进行10次重复实验并计算综合评价指标F的平均值，实验结果如图5所示.

初始化样本点个数k与准确率、精确率召回率评价指标关系的实验结果如表1所示.

上述实验表明，当参数k取值为100时异常值检测效果最佳.参数k的取值过小或者过大，都会使得综合评价指标F的值降低，这代表异常值检测效果降低.原因如下：参数k的取值不能过小，一方面是因为参数k实际上决定了RRCT结构的规模和随机分割的次数，如果随机分割次数不多，对于异常样本点其产生叶子结点深度的变化情况则不显著，进而导致异常评分普遍降低，异常点和正常点的异常评分差异不显著，进而难以区分异常样本点和正常样本点，从而导致整体召回率下降;另一方面是基于RRCF算法随机分割的特性，如果RRCT结构规模过小则对于异常点识别的稳定性大幅下降，失去对异常值检测的参考价值.参数k的取值同样不能过大，由于变压器损耗数据实际上是存在一定正常波动的，RRCT结构如果规模太大则会导致随机分割过细，进而导致对于异常的灵敏度过高，即使正常的数据波动也会导致对应样本点的异常评分升高，将许多正常点认定为异常，进而降低整体精确率.综上所述，通过实验可以认定当参数k取值为100时，异常值检测效果较为理想.

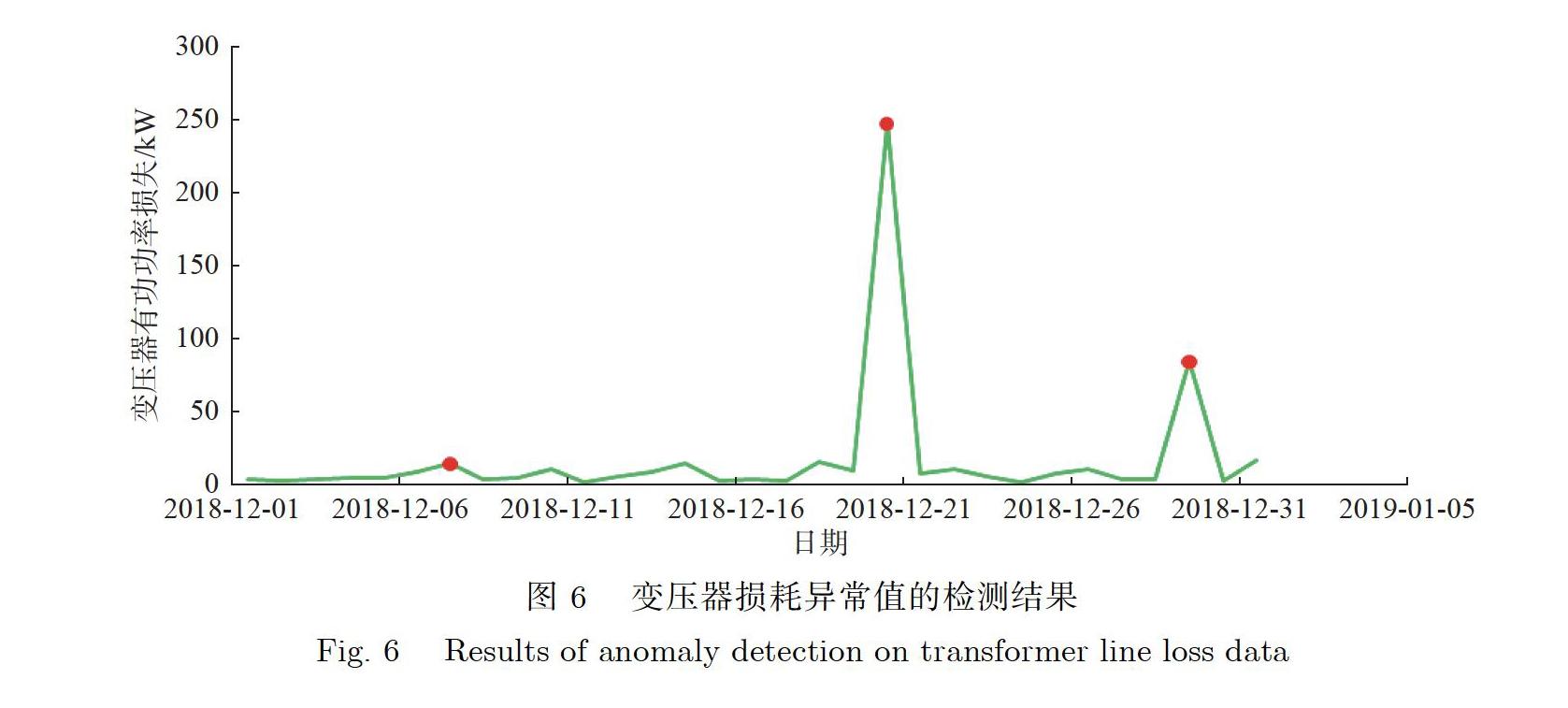
运行基于RRCF算法的变压器损耗异常值检测算法，设置初始化样本点个数k=100，获得异常评分阈值为18.20，对剩余数据计算异常评分并以该阈值作为参照，以筛选异常样本点，最终在942个样本中检测出19个异常样本点，变压器损耗数据集在某一时间段的异常值检测结果如图6所示.

由图6可以看出，当变压器损耗发生异常突变的时候，本文所述方法可以很好地识别这样异常的变化情况，其检测结果与实际异常发生情况是吻合的，说明本文所述方法对变压器损耗数据的异常值检测具有可行性.

3.4.3实验对比

对于初始变压器损耗数据集，分别使用本文所述的方法，孤立森林算法以及基于DBSCAN聚类的异常值检测算法进行异常值检测，3种算法的对比检测结果如表2所示.

分析结果显示，本文方法对于变压器损耗数据的异常值检测，准确度较高，相较于孤立森林算法和基于DBSCAN聚类的异常值检测分别提高1.61%和4.97%.本文所述方法对异常点的识别和覆盖效果好，召回率可以达到100%，能够完全检测到异常样本点.本文所述方法对于异常样本的敏感程度适中，精确率相较于孤立森林算法提高显著，提高了22.26%.综上所述，本文所述方法相较于孤立森林算法和基于DBSCAN聚类的异常值检测算法，在变压器损耗数据异常检测方面具有较好的效果.

4结论

本文基于RRCF算法，实现了对于变压器损耗的异常值检测方法，提出了对于动态数据流的实时变压器损耗数据的检测模型.基于RRCF算法的变压器损耗异常值检测方法具有较好的运行效率，且对大量值动态数据流具有较好的适应性.本文将该算法应用于处理变压器损耗数据的异常值检测，实验表明异常检测效果好，本文所述的方法具有较好的理论和应用价值.

[参考文献]

[1]王忠杰，文乐，杨新民.大数据在智能化电厂中的应用研究与展望[J].中国电力，2019，52（3）：133-139.

[2]李炳森，胡全贵，陈小峰，等.电网企业数据中台的研究与设计[J].电力信息化，2019，17⑺：29-34.

[3]林鸿，方学民，袁葆，等.电力物联网多渠道客户服务中台战略研究与设计[J].供用电，2019，36（6）：39-45.

[4]SUNDARARAJAN A，HERNANDEZ A S，SARWAT A I. Adapting big data standards，maturity models to smart grid distributedgeneration：Critical review [J]. IET Smart Grid，2020，3（4）：508-519.

[5]PASSERINI F，TONELLO A M. Smart grid monitoring using power line modems：Effect of anomalies on signal propagation [J]. IEEE Access，2019（7）：27302-27312.

[6]刘树仁，宋亚奇，朱永利，等.基于Hadoop的智能电网状态监测数据存储研究[J].计算机科学，2013，40（1）：81-84.

[7]HUO Y，PRASAD G，ATANACKOVIC L，et al. Cable diagnostics with power line modems for smart grid monitoring [J]. IEEE Access，2019（7）：60206-60220.

[8]WITTEN I H，FRANK E，HALL M A，et al. Data Mining：Practical Machine Learning Tools and Techniques [M]. 4th ed. San Francisco：Morgan Kaufmann，2016.

[9]COSTA D，PORTELA F，SANTOS M F. An overview of data mining representation techniques [C]// Proceedings of the 2019 7th International Conference on Future Internet of Things and Cloud Workshops. IEEE，2019：90-95.

[10]AKOGLU L，TONG H，KOUTRA D. Graph based anomaly detection and description：A survey [J]. Data Mining & Knowledge Discovery，2015，29（3）：626-688.

[11]CHANDOLA V，BANERJEE A，KUMAR V. Anomaly detection for discrete sequences：A survey [J]. IEEE Transactions on Knowledge & Data Engineering，2012，24（5）：823-839.

[12]TRAN T N，DRAB K，DASZYKOWSKI M. Revised DBSCAN algorithm to cluster data with dense adjacent clusters [J]. Chemometrics &Intelligent Laboratory Systems，2013，120：92-96.

[13]王文红，李惊涛，陈俊彦，等.基于聚类算法对异常事件分析评价电能表整体状态的方法：CN201310624924.4 [P]. 2014-03-12.

[14]LIU F T，TING K M，ZHOU Z. Isolation forest [C]// 2008 Eighth IEEE International Conference on Data Mining. IEEE，2008：413- 422.

[15]余翔，陈国洪，李霆，等.基于孤立森林算法的用电数据异常检测研究[J].信息技术，2018，42（12）：88-92.

[16]GUHA S，MISHRA N，ROY G，et al. Robust random cut forest based anomaly detection on streams [C]// International Conference on Machine Learning. PMLR，2016：2712-2721.

[17]INOUE J，YAMAGATA Y，CHEN Y，et al. Anomaly detection for a water treatment system using unsupervised machine learning [C]// Proceedings of the 2017 IEEE International Conference on Data Mining Workshops. IEEE，2017：1058-1065.

[18]BARTOS M，MULLAPUDI A，TROUTMAN S. RRCF：Implementation of the robust random cut forest algorithm for anomaly detection on streams [J]. Journal of Open Source Software，2019，4（35）：1336.

[19]WANG Y，WANG Z，XIE Z，et al. Practical and white-box anomaly detection through unsupervised and active learning [C]// 2020 29th International Conference on Computer Communications and Networks. IEEE，2020. DOI：10.1109/ICCCN49398.2020. 9209704.

[20]BOX G E P，JENKINS G M，REINSEL G C，et al. Time series analysis：Forecasting and control [J]. Journal of the Operational Research Society，2015，22（2）：199-201.

[21]HABEEB R A A，NASARUDDIN F，GANI A，et al. Real-time big data processing for anomaly detection：A survey [J]. International Journal of Information Management，2019，45：289-307.

（責任编辑：陈丽贞）