高阶shifted调和数的有限求和
闫庆伦 王照芬 米娟








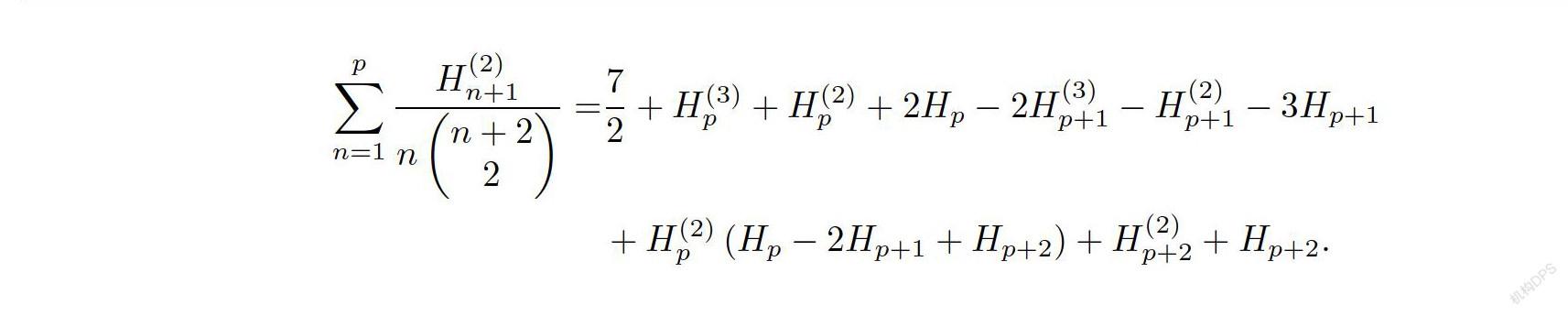
摘要:在本文中,我们利用部分分式法等方法研究了一组关于Euler型求和的组合恒等式,计算了有关高阶shifted调和数与二项式系数的倒数的乘积的有限求和形式.通过对参数取特殊值,可以得到许多有意义的恒等式.
关键词:调和数;二项式系数;部分分式法
中图分类号:O157文献标志码:ADOI:10.3969/j.issn.l000-5641.2021.06.003
Finite sums in higher order powers of shifted-harmonic numbers
YAN Qinglun,WANG Zhaofen,MI Juan
(College of Science^ Nanjing University of Posts and Telecommunications. Nanjing 210023. China)
Abstract:In this article,using methods such as the partial fraction method,we study a set of combined identities for an Euler-type summation. We calculate,furthermore,the finite summation form of the product of the high order shifted-harmonic number and the reciprocal of the binomial coefficient. By using special values for the parameters,interesting identities can be obtained.
Keywords:harmonic numbers;binomial coefficient;the partial fraction method
0引言
令、、分别表示实数集、复数集和正整数集.经典调和级数定义如下:
或者,
其中γ是Euler-Mascheroni常数,ψ(z)是Psi(或者Digamma)函数.
广义调和级数的定义为:
在广义调和级数的下标为非整数值的情况下,例如,可以根據Polygamma函数[1]定义广义调和级数,其中Polygamma函数的定义为:
其中ζ(z)是Riemann Zeta函数.在上式中,当m=0时,我们将定义为:
下面是一些关于此类调和级数的具体例子.
其中G=0.915965…是Catalan常数.
本文将讨论高阶shifted调和数与二项式系数倒数乘积的有限项求和,其形式如下:
与这种Euler型无穷级数类似的级数许多学者已研究过,如Sofo[2]得到了下列恒等式:
Sofo[3]还得到了如下经典的Euler求和:
有关高阶调和数的有限求和形式也已经被多次研究.如在2005年,Weideman[4]猜测了如下形式的调和数恒等式:
这个式子曾经被认为是最难证明的,后来由Driver等[6]利用计算机给出了证明.最近,Sofo[6-7]又得到了许多有关Euler型有限项求和的恒等式,如
关于调和数更多的计算与结论,请参考文献[8-10].
下面给出的引理在文中主要定理的证明过程中起着非常重要的作用.
1引理
引理1[8]令r是一个正整数,p∈N,则下列等式成立:
注当p=1时,,其中[x]是不超过实数x的最大整数.
下面,我们将用上述引理和部分分式法等来证明主要定理.
2主要定理及特例
定理1令m,k∈N,,则下列恒等式成立:
证明为了方便计算,我们引入如下变换:
那么
根据二项式系数的定义,并利用部分分式法,不难得到
其中
则
注意到,对于任意双序列{X},有下列恒等关系成立:.于是,我们有
结合式(2.2),式(2.1)右边的第二项求和式可进行如下计算:
将上面两部分计算结果代入式(2.1),整理后即得定理1.
在定理1的假设下,当q=±1时,我们得到了如下两个重要推论.
推论1令,则有
证明首先考虑q=1的情况.
其中
根据部分分式法:
有
将上面的式子以及式(2.4)代入式(2.3)中,整理得到推论1中的第一个恒等式.
接下来考虑q=-1的情况.
根据部分分式法,有
应用上面的式(2.7)与式(2.8),得到
将式(2.4)和式(2.9)代入式(2.6),得到推论1中的第二个恒等式.
同理,参照定理1和推论1的证明,我们可以得到定理2和推论2.
定理2令,,理则下列恒等式成立:
注当m=1或2时,Sofo[9-10]计算过类似的结果,不过等号右边的表现形式略有不同.
推论2令,那么有
在上述定理和推论中将参数取特殊值,可以得到许多有意思的恒等式.
例1在定理1中令q=4,m=1,k=2,得到
例2在定理1中令q=±4,m=3,k=2,则有
例3在推论1中令m=2,k=3,得到
例4在定理2中,令m=3,q=-4,k=2,则有下列式子成立:
例5在推论2中,令m=2,k=2,则有
[参考文献]
[1]SRIVASTAVA H M,CHOI J. Zeta and q-Zeta Functions and Associated Series and Integrals [M]. Amsterdam:Elsevier Science Publishers,2012.
[2]SOFO A. Quadratic alternating harmonic number sums [J]. Journal of Number Theory,2015,154:144-159.
[3]SOFO A. Harmonic sums and integral representations [J]. Journal of Applied Analysis,2010,16:265-277.
[4]WEIDEMAN JAC. Pade approximations to the logarithm I:Derivation via differential equations [J]. Quaestiones Mathematicae,2005,28(3):375-390.
[5]DRIVER K,PRODINGER H,SCHNEIDER C,et al. Padéapproximations to the logarithm II:Identities,recurrences,and symbolic computation [J]. Ramanujan Journal,2006,11(2):139-158.
[6]SOFO A. Identities for alternating inverse squared binomial and harmonic number sums [J]. Mediterranean Journal of Mathematics,2016,13(4):1407-1418.
[7]SOFOA.Finite sums in higher order powers of harmonic numbers [J]. Bull Math Anal Appi,2013(5):71-79.
[8]XU C.Explicit evaluation of harmonic sums [J]. Communications of the Korean Mathematical Society,2017,33(1):13-36.
[9]SOFOA,SRIVASTAVA H A I. A family of shifted harmonic sums [J]. Ramanujan Journal,2015,37(1):89-108.
[10]SOFOA.Shifted harmonic sums of order two [J]. Communications of the Korean Mathematical Society,2014,29(2):239-255.
(責任编辑:林磊)

