平面壁画高分辨率图像的快速特征匹配方法

章昕烨 童卫青 李海晟

摘要：既有的图像特征匹配算法比较适合于一般分辨率的图像，且是在灰度图像上进行的.洞窟壁画图像的特点是分辨率非常高，并且还可能存在具有相同灰度纹理和不同颜色的区域.针对这类特殊图像，提出了一种面向高分辨率壁画图像的高速化特征匹配算法（简称NeoKPM算法）.NeoKPM算法有2个主要特点：①通过降采样图像获得原图像粗配准的单应变换矩阵，极大地降低了后续特征匹配的时间复杂度;②提出了一种基于灰度和颜色不变量的特征描述符，能很好地区分具有相同灰度纹理和不同颜色的特征点，提高了特征匹配的正确性.在实际壁画图像库上，对NeoKPM算法的性能进行了实验.实验结果表明，NeoKPM算法在分辨率为8 000万像素的壁画图像上，其每对图像的正确匹配点数量平均比SIFT（Scale Invariant Feature Transform）算法高出了近10万个;其特征点匹配平均处理速度是SIFT算法的20倍;其基于图像单个像素的双图像平均误差小于0.04像素.

关键词：壁画数字化;特征匹配;暴力匹配;颜色不变量

中图分类号：TP391文献标志码：ADOI：10.3969/j.issn.l000-5641.2021.06.008

A fast key points matching method for high resolution images of a planar mural

ZHANG Xinye1，TONG Weiqing1，2，LI Haisheng1

（1. School of Computer Science and Technology. East China Normal University，Shanghai 200062. China;

2. Shanghai Commercial Digital Printing Co.，Ltd. Shanghai 200041，China）

Abstract：Existing methods of key points matching were invented for grayscale images and are not suitable for high resolution images. Mural images typically have very high resolution，and there may be areas with the same gray textures and different colors. For this special kind of image，this paper proposes a high-speed algorithm of key points matching for high-resolution mural images （NeoKPM for short）. NeoKPM has two main innovations：（1）first，the homography matrix of rough registration for the original image is obtained by downsampling the image，which substantially reduces the time required for key points matching;（2）second，a feature descriptor based on gray and color invariants is proposed，which can distinguish different colors of texture with the same gray level，thereby improving the correctness of key points matching. In this paper，the performance of the NeoKPM algorithm is tested on a real mural image library. The experimental results show that on mural images with a resolution of 80 million pixels，the number of correct matching points per pair of images is nearly 100 000 points higher than that of the SIFT （Scale Invariant Feature Transform）algorithm，the processing speed of key points matching is more than 20 times faster than that of the SIFT algorithm，and the average error of dual images based on a single pixel of theimage is less than 0.04 pixels.

Keywords：mural digitizing;key points matching;brute force matching;color invariance

0引言

洞窟壁畫是人类的艺术瑰宝，数字化保存是其重要的保护方法.根据我国国家文物局关于古壁画的一级影像采样分辨率不低于300 DPI（Dots Per Inch，每英寸点数）的技术要求[1]，目前任何高分辨率的相机都无法通过拍摄一幅图像来保存大幅面的洞窟壁画.因此，一般采用划分壁画采集区块的方法，即把一幅大幅面的壁画划分成n×m大小的有重叠的采集区块，然后对每一区块用高分辨率相机进行拍摄，再通过图像拼接方法把这些采集区块的图像（一般有上百幅图像）拼接成一幅全景图像.图像拼接的主流方法是通过寻找图像匹配点，然后通过匹配点把图像对齐后实行拼接处理.为此，如何找到2幅图像的稳定而可靠的特征点，并进行有效的特征点匹配是图像拼接中非常重要的处理环节，因为这直接影响着图像拼接的精度和效果.

特征点匹配包括3个处理过程：图像特征点检测、图像特征点描述和图像间的特征点匹配.关于特征点检测和描述的研究比较成熟，经典的方法有SIFT[2]算法、MSER（Maximally Stable Extremal Region）[3]算法、SURF（Speeded-Up Robust Features）[4]算法、ORB（Oriented FAST （Features from Accelerated Segment Test）and Rotated BRIEF （Binary Robust Independent Elementary Features））[5]算法等.文献[6]对主流的特征点检测算法做了全面的比较研究后指出，SIFT算法在旋转和尺度不变性方面是最好的.主流的特征点检测算法主要适用于灰度图像，也就是说这些算法都没有考虑如何处理具有相同灰度纹理却有着不同色彩信息的图像.MSER算法在理论上可以直接检测到彩色图像的特征斑点，但其检测性能比从灰色图像检测要差许多.CSIFT （Colored SIFT）[7]算法是为了解决能从彩色图像上直接检测特征点而被提出来的，该算法通过把彩色图像变换为基于颜色不变量的灰度图像[8]，从而类似SIFT算法一样实现了彩色图像的特征检测和描述.由于基于颜色不变量的灰度图像纹理比彩色图像的纹理要粗糙很多，所以导致了CSIFT算法检测出来的特征点数量比用SIFT算法检测出来的数量要少很多，而特征点数量又对后续的特征点匹配的精度影响比较大.与利用线性高斯金字塔来构建多尺度空间以检测关键特征点的SIFT算法和SURF算法不同，KAZE[9]算法采用加性算子分裂（Additive Operator Splitting，AOS）算法来进行非线性的扩散滤波，从而构造出非线性尺度空间，具有比较好的特征点可重复检测特性，但是也付出了高昂的計算成本.在后续研究中虽然提出了加速版的A-KAZE（Accelerated KAZE）[10]，但其特征检测性能不如KAZE，其尺度不变性不如SIFT鲁棒，不太适合应用于高分辨的壁画图像.相较于SIFT利用高斯差分（Difference of Gaussians，DoG）算子检测特征点，2020年Cho等[11]提出了一种特征检测算法，该算法引入了高斯拉普拉斯（Laplacian of Gaussian，LoG）算子及其高阶导数（HLoG）来构造尺度空间，并对其特征检测进行了实验验证，取得了比较好的结果;但该算法对具体图像的参数确定比较困难，稳定性方面也存在问题，因而还达不到实用的要求.在深度学习领域中，近几年也提出了一些新颖的特征检测和描述算法[12-14]，但这些算法存在着两个棘手问题：一是需要大量的训练样本;二是泛化性还没有解决，所以暂时还不适合应用于样本非常稀缺的洞窟壁画上.

特征点匹配可以分为初匹配和匹配验证两个阶段：第一阶段比较主流的初匹配方法是暴力匹配法（Brute Force Matching，BFM），该方法对每个特征点生成一个特征描述向量（也称特征描述符），对每个特征点用全遍历方式从另一幅图像里寻找与该特征点的特征向量最相似的特征点作为其匹配点对;第二阶段的匹配验证的目的是消除在初匹配中的误匹配点对，通常使用随机抽样一致算法（Random Sample Consensus，RANSAC）[15]和最小二乘方回归算法（Least Median of Squares，LMedS）[16].

从理论角度来说，如果初匹配中野点数（离群点）与内点数之比较高时（一般为大于50%），那么基于上述两种算法验证后的匹配精度就会降低，甚至很差.后来又相继提出了一些改进的方法，例如，Fotouhi等[17]根据特征描述最相近与次相近的匹配点之间的距离比来构造一组可靠的特征匹配点，并用这些基准点来区分正确点和离群点;Lin等[18]根据正确匹配点之间的相干性（Coherence Property），再通过一种非线性回归的方法来去除离群点;Chou等[19]提出了一种分两阶段进行抽样和平面投票的匹配法，用于剔除离群点.但是这些方法几乎都是针对验证处理，不能减少第一阶段的无效匹配，只能消除错误的对应关系.另外，通过实验还发现，在特征点匹配处理中，暴力匹配的计算时间成本占据了整个处理过程的80%.

根据以上分析，本文解明了目前图像特征点匹配的主流算法中存在的问题：①特征点检测算法对灰度图像比较有效，但对彩色图像效果不好;②初匹配的时间消耗占整个图像匹配过程的80%左右;③当野点较多时，RANSAC算法的效果会明显下降.上述这些问题，当2幅图像的分辨率不高时，其对图像拼接精度的影响基本上显现不出来;但对大幅面壁画图像拼接来说，其对拼接精度和时间复杂度的影响就非常显著了.

既有的图像特征点匹配算法比较适合于一般分辨率的图像，且是在灰度图像上进行的.洞窟壁画图像的特点是分辨率非常高，并且可能存在具有相同灰度纹理而颜色不同的区域.针对这类特殊图像，本文提出了一种面向大幅面、高分辨率壁画图像的高速化特征点匹配算法（简称NeoKPM算法）. NeoKPM算法有2个主要特点：①通过降采样图像获得原图像粗略配准的单应变换矩阵，极大地降低了后续特征点匹配的时间复杂度;②提出了一种基于灰度和颜色不变量的特征描述符，它能很好地区分具有相同灰度纹理不同颜色的特征点，提高了特征点匹配的正确性.

在实际人工壁画图像库上，本文对NeoKPM算法的性能进行了实验.实验结果表明，NeoKPM算法在分辨率为8000万像素的壁画图像集上，其每对图像的正确匹配点数量平均比SIFT算法高出近10万个，其特征点匹配处理速度是SIFT算法的20倍，其基于图像单个像素的双图像平均误差小于0.04像素.

1NeoKPM算法

本章首先给出NeoKPM算法的原理和整个算法，然后用实验考察降采样率与图像配准误差的关系，最后叙述颜色不变量在特征匹配中的作用.

1.1原理和算法

特征点匹配是图像拼接中的关键处理环节，匹配准确与否对后续无论是2维拼接还是3维重建都是至关重要的.本文提出的匹配算法分为特征粗匹配和特征精匹配两个阶段.

由于采集的原始壁画图像具有很高的分辨率（一般在8000万像素以上），而既有的特征点匹配算法对这类图像处理的时间复杂度很高（一般需要几小时），其原因是高分辨率图像会检测出大量特征点，而特征点的匹配是采用暴力匹配法.为了提高特征匹配的速度，必须考虑把图像的分辨率大幅度下降，但是分辨率下降的图像又会影响特征匹配的精度.为了克服这一矛盾，我们先对2幅输入图像进行降采样处理.根据1.2节中的实验数据，按10%的降采样率进行降采样后的图像（即比原图像缩小了100倍）所获得的平均配准误差在1像素左右，但其处理时间大幅度下降（约下降20倍）.为此，第一阶段，先通过降采样图像获得原图像的单应变换矩阵，即特征粗匹配;第二阶段，先检测出2幅输入图像的特征点，然后利用特征粗匹配的单应变换矩阵来确定每个目标图像中的每个匹配点在参考图像中的对应位置，而后在一个5×5的矩形区域内，搜索其匹配点，这样就可以获得既高速又高精度的特征点匹配.

下面给出完整的NeoKPM算法.

第一阶段特征点粗匹配

（1）对输入的2幅重叠图像（分别为目标图像和参考图像，目的是用目标图像去配准参考图像）进行降采样处理（一般降采样率为10%，即对原始图像缩小100倍），分别输出目标图像的降采样图像T和参考图像的降采样图像R.

（2）根据2幅图像拍摄时的重叠率（对于同一幅壁画，其拍摄重叠率是固定的）估算降采样图像T和降采样图像R间的粗略平移量和重叠区域，并依据图像重叠率计算后续匹配模板的大小.

（3）在降采样图像T的重叠区域中央，选取指定大小的矩形区域作为匹配模板，在降采样图像R的重叠区域内搜索与匹配模板最相似的区域的位置，据此得到降采样图像T和降采样图像R间的最大平移量.

（4）分别生成降采样图像T和降采样图像R的灰度图像和颜色不变量图像.

（5）分別从降采样图像T和降采样图像R的灰度图像中检测出SIFT特征点.

（6）根据SIFT特征点的位置，分别从降采样图像T和降采样图像R的灰度图像与颜色不变量图像中抽出基于SIFT描述符的联合特征向量.

（7）对降采样图像T中每个特征点，根据最大平移量可以估计出它在降采样图像R_s上的对应矩形范围，然后进行基于联合特征向量的特征点匹配搜索，找到其对应的匹配点.

（8）找到2幅图像中对应的点对集合，再根据降采样图像与原图像之间的几何关系，将降采样图像坐标系下的匹配点集合中的所有特征点映射到原图像坐标系下，利用RANSAC算法估计原分辨率图像间的初始单应变换矩阵H，从而获得目标图像和参考图像间的单应变换关系.

第二阶段特征点精配准

（9）对2幅输入图像分别生成参考图像与目标图像的灰度图像和颜色不变量图像，记参考图像的灰度图像、目标图像的灰度图像、参考图像的颜色不变量图像、目标图像的颜色不变量图像分别为T、R、T、R.

（10）分别在图像T、R上检测其SIFT特征点.

（11）在目标图像的灰度图像以及颜色不变量实数图上，计算所有特征点的SIFT特征向量，然后把每个特征点的灰度特征向量和颜色不变量特征向量拼接成256维的联合SIFT特征向量.

（12）在参考图像的灰度图像以及颜色不变量实数图上，计算所有特征点的SIFT特征向量，然后把每个特征点的灰度特征向量和颜色不变量特征向量拼接成256维的联合SIFT特征向量.

（13）对目标图像和参考图像里的特征点按以下步骤进行初匹配处理：对图像T中每个特征点，根据第一阶段得到的图像粗配准的单应变换矩阵H可以估计出它在图像R上位置;然后在以该位置为中心的5×5矩形范围内，用其对应的联合SIFT特征向量的相似度来寻找匹配点.

（14）用RANSAC算法对上述找到的所有匹配点进行筛选，获得真匹配点集合，然后根据这些真匹配点集合计算目标图像和参考图像间的单应变换矩阵H，完成输入图像的特征点匹配.

1.2图像降采样率与特征点匹配精度

当前特征点的初匹配几乎都是通过基于特征描述符距离的暴力匹配方法来完成的，其计算时间取决于图像特征点的数目.SIFT特征点是在多尺度空间下的局部极值点[2]，其数量与图像的尺寸和纹理复杂度相关联.在超高分辨率（一般在8 000万像素以上）的原始壁画图像上检测出的SIFT特征点数量可达到百万级别，也就是说暴力匹配法需要计算多维特征向量距离的次数将高达万亿次，实验中实际测得的处理时间约为3 h.图像分辨率的减小会直接影响像素层级进而导致原图像纹理被压缩，部分特征点将无法被检测出来.表1所示为，对分辨率为（10 288×7 730）像素的超分辨壁画图像进行多次降采样处理后，降采样图像上检测出的SIFT特征点数量的变化情况.表1的数据表明，特征点的数量随着降采样率的增大而显著减少.

降低图像分辨率可以大幅度降低特征匹配的时间复杂度，但同时也会影响特征匹配的精度.为了解决这一问题，需要对降采样率与特征点匹配精度之间的关系进行实验考察：首先，对图像库A（见2.1节的图像库说明）中的所有参考图像和目标图像分别按5%的递减步长进行降采样;然后对降采样后的参考图像和目标图像，分别计算各个降采样图像以及原图像的特征点匹配的处理时间和误差.本文参考的基准算法是SIFT，实验中，基于图像库A中已知的单应变换矩阵计算降采样图像和原图像的特征点匹配误差，并以两者的相对双向平均误差来衡量因降采样所产生的特征点匹配误差.

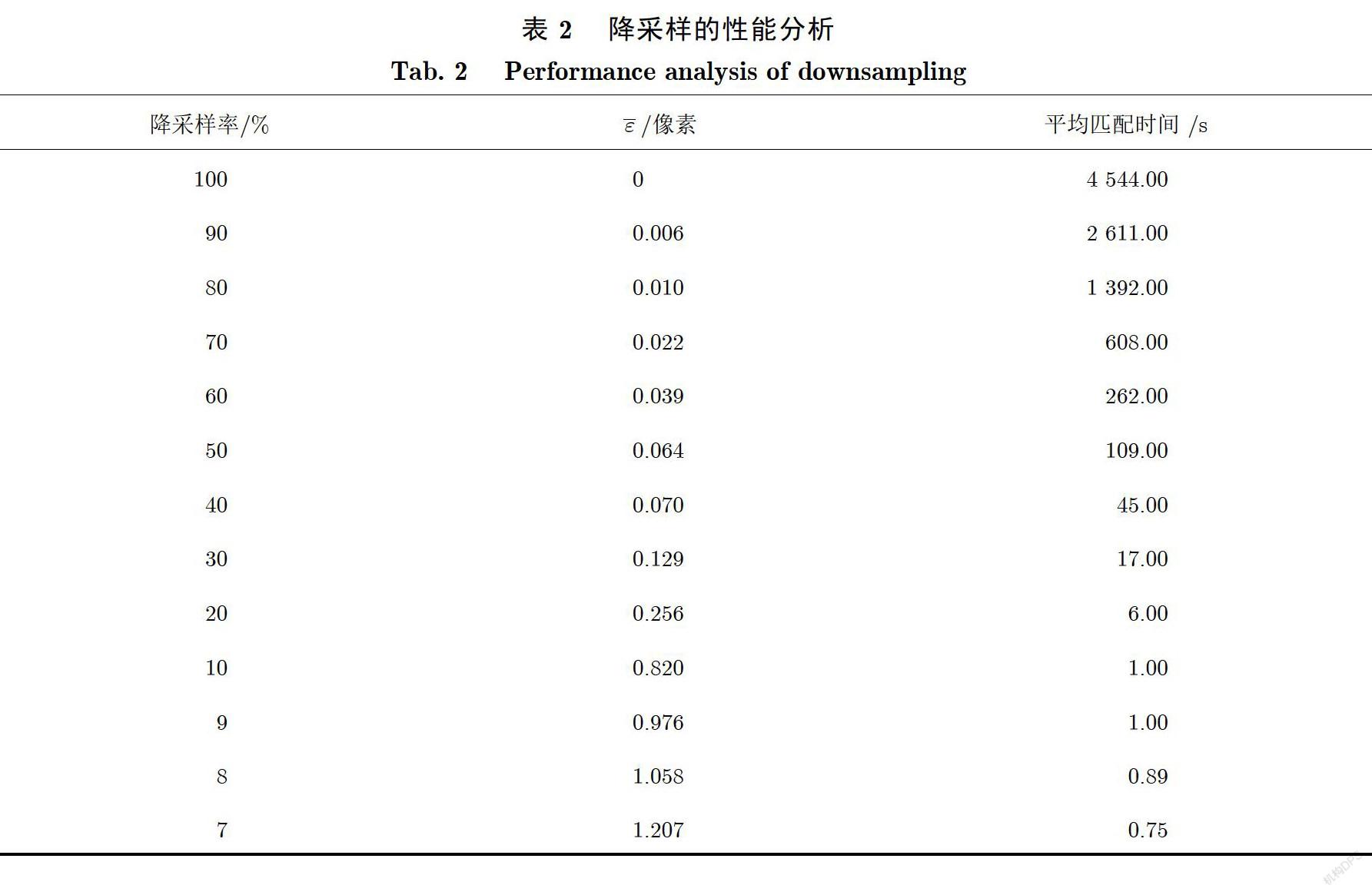
表2所示是对图像库A中100对图像进行降采样性能考察的实验结果.实验结果表明，在降采样率为10%时，降采样图像的特征点匹配误差与原图像特征点匹配误差的相对双向平均误差为0.82像素，降采样图像的平均匹配时间约为1.0s（原图像的平均匹配时间为4 544s，约为原分辨率图像特征点匹配时间的万分之三）.

为了进一步验证上述实验结论的一般性，本文对与图像库A中具有不同分辨率和纹理的另外200幅壁画图像进行了相同的实验，实验结果如表3所示.从表3可知，在降采样率为10%时，其特征点匹配误差与原图像的特征点匹配误差的相对双向平均误差保持在1像素左右，降采样图像的平均匹配时间约为0.69s（原图像的平均匹配时间为139.80 s，约为原分辨率图像特征点匹配时间的千分之五）.根据以上两个实验数据，本外文认为对高分辨率的图像取10%的降采样率比较合适.

1.3颜色不变量

颜色是区分图像纹理差异的重要信息，与视角、光照方向、光照强度、表面方向和菲涅尔反射系数等因素高度关联.这些因素导致了目标物体上具有相同颜色的区域，但在图像中却呈现出颜色略微不同的几个区域.为了解决这个问题，Geusebroek等[8]提出了公式（1）和公式（2）所示的颜色不变量H，公式具体为

公式（1）和公式（2）中，E、E、E分别是光谱能量、光谱能量的一次导数和光谱能量的二次导数，R、G、B是目标物的颜色.Geusebroek等证明了在等能量的不均匀光照条件下，颜色不变量H是一个独立于视角、光照方向、光照强度、表面方向和菲涅尔反射系数的物体反射不变量.

为了解明基于灰度信息和颜色不变量H的联合SIFT特征向量（简称GHIFT特征向量）对颜色变化的辨别能力，本文设计了如下实验方案.

（1）从图像库D中读取1幅图像，按照图1（a）的方式拼接成上下2幅相同的图像，并把该拼接后的图像作为参考图像，复制参考图像得到目标图像.

（2）用SIFT算法分别从参考图像和目标图像上检测特征点.

（3）实验中，始终保持参考图像和目标图像的上半部不变，在保持灰度值I=0.3R+0.59G+0.11B基本不变的条件下，6次随机改变目标图像下半部颜色的R、G、B分量值，并保证R、G、B分量值中至少有1个值的变化绝对值分别不小于5%、10%、15%、20%、25%、30%.

（4）每次目标图像的下半部的颜色发生变化时，用前面介绍过的联合SIFT特征向量进行特征点匹配处理，获得当前2幅图像的匹配点数量.

（5）将当前2幅图像的匹配点数与原来2幅图像的特征点数进行比较，从而考察该颜色不变量的联合SIFT特征向量对颜色变化的敏感度.

理论上，当颜色没有变化时，参考图和目标图是完全一样的，并且每幅图的上半部与下半部也是完全相同的，因此，目标图上的每个特征点都可以在参考图上找到2个匹配点;当目标图的下半部的颜色变化时，目标图上的每个特征点都只能在参考图上找到1个匹配点.

对图像库D（见2.1节的图像库说明）的100幅图像进行了实验.实验结果表明，基于灰度信息的SIFT特征向量不能去除下半部误匹配点;而基于联合SIFT特征向量几乎可以去除所有下半部误匹配点，如图1（b）所示.图2是颜色变化从5%变到30%时，联合SIFT特征向量对误匹配点的去除比例，其中横轴表示颜色变化的比例，纵轴表示联合SIFT特征向量对误匹配点的去除能力.

2实验评估

实验环境为，Core i7-8700k处理器，32 GB内存;Windows 10操作系统;开发工具为Visual Studio 2015 community;使用OpenCV3.3.0.

2.1实验图像库的制作

本文所有图像库的原始图像均来自新疆龟兹洞窟的实际壁画.

2.1.1图像库A

图像库A包含100对重叠图像（即200幅图像），其中100幅是原始壁画图像，记为参考图像集（图3（a）），A里有33幅分辨率为（10288×7730）像素的图像，其余67幅圖像的分辨率为（5087×3703）像素.根据不同的单应变换矩阵，将A里的每一幅图像分别生成其对应的重叠图像，记为目标图像集A，如图3（b）所示.

2.1.2图像库B

图像库B由50对具有不同重叠率的图像组成（即100幅图像），其中10对图像的分辨率为（10288×7730）像素，其余40对图像的分辨率为（5087×3703）像素.这100幅图像中50幅是原始壁画图像，记为参考图像集B（图3（c））;另外的50幅是与B中有部分重叠的壁画图像，记为目标图像集B（图3（d））.

2.1.3图像库C

图像库C由200幅图像构成：从图像库A的参考图像集A中，采用定位截取的方式构造100幅大小为（640×480）像素的图像，记为参考图像集C（图3（e））;另外100幅图像是由C根据不同的单应变换矩阵分别生成的，记为目标图像集C（图3（f））.

2.1.4图像库D

从图像库A中的33幅分辨率为（10288×7730）像素的壁画图中，采用定位截取的方式截取100幅分辨率为（1 024×512）像素、纹理较为丰富的图像作为图像库D，如图3（g）所示.

2.2NeoKPM算法与SIFT算法、SURF算法、ORB算法和SC-RANSAC算法的性能比较

本节的实验目的是将NeoKPM算法与特征点匹配的经典算法SIFT、SURF、ORB和在匹配验证阶段做出最新改进的SC-RANSAC（Spatial Consistency RANSAC）[17]进行比较，考察NeoKPM算法在特征匹配的时间、特征匹配点的数量和特征匹配的误差方面的性能.

2.2.1在图像库A上的考察实验

使用上述5种算法对图像库A中的100对重叠图像进行特征匹配，分别记录各类算法在两两图像对上特征匹配的时间、特征匹配点的数量和特征匹配的误差.由于图像库A中两两图像对之间的单应变换矩阵已知，所以可以使用对称转移误差[20]来评估各算法的匹配精度.这里计算了图像中每一个像素的对称转移误差.为了评估各算法的误差分布情况，实验中将（0.005～0.100）像素范围以0.005为间隔分成19个等距的区间，如0.005～0.010，同时增设0.100～1.000、>1.000这两个较大的特殊区间来统计离群数值，分别记录5类算法在每对图像上的平均误差在各个区间的图像数量百分比，如图4所示.图4中横轴表示平均误差统计区间，纵轴表示误差分布的数量百分比.实验数据表明，NeoKPM算法的误差几乎都小于0.04像素，并且比所有其他方法都要好.表4是5种算法在图像库A上获得的最小平均误差图像的数量统计.数据表明，NeoKPM算法在大多数图像上产生的特征匹配误差比其他4种算法要小.

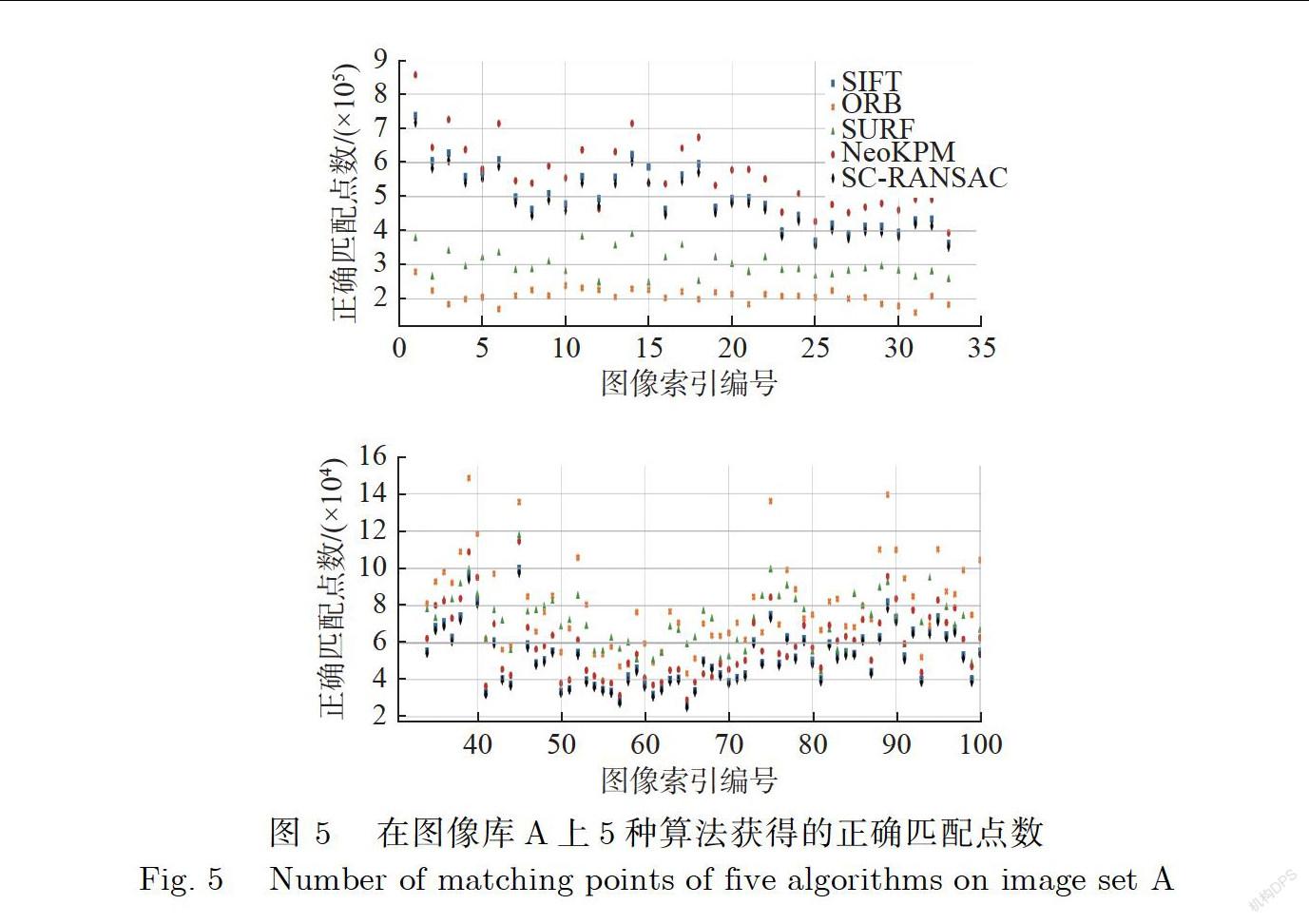
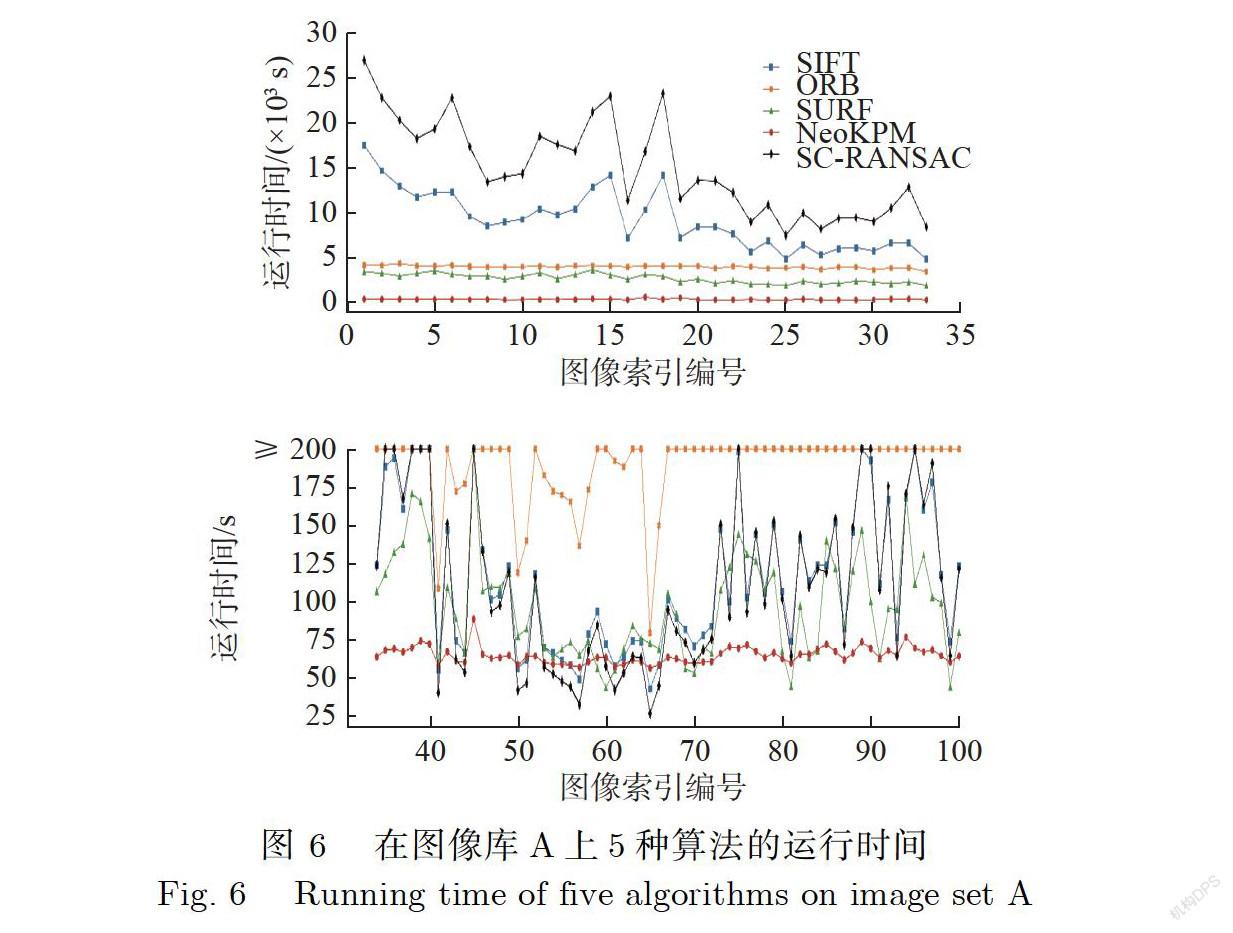
在图像库A上的5种算法的正确匹配点数和运行处理时间分别如图5和图6所示，其中横轴为图像库A中图像对的图像索引编号.

由于图像库A中存在两种分辨率的图像，因此本文对实验数据进行了分类整理，图5和图6的上半部为在33对分辨率为（10288×7730）像素图像上实验得出的数据，下半部为在67对分辨率为（5087×3703）像素的图像上实验得出的数据.从实验中可以得出，NeoKPM算法能够以最少的运行时间在纹理较为丰富的高分辨率（（10288×7730）像素）壁畫图像上获得最多数量的匹配点.结合表5和表6的数据可以得出，NeoKPM算法在纹理不明显、分辨率较低（（5087×3703）像素）的图像上，不仅可以较为稳定地获取精度和数量比较好的匹配点，并且其63.37s的平均处理时间低于其他4种算法.

2.2.2在图像库B上的考察实验

2.2.1节考察了5种算法在2幅图像的单应变换矩阵已知条件下的匹配误差情况.本节考察2幅图像在其单应变换矩阵未知条件下的匹配误差情况，而图像库B就是符合这个条件的图像库.由于不知道2幅图像的单应变换矩阵，无法计算每个特征点的匹配误差，所以本文采用肉眼观察的方法：2幅有重叠的图像通过匹配点对齐后，如果没有明显错位就认为是特征匹配成功.在图像库B上，5种算法的匹配成功的结果如表7所示.由表7可知，NeoKPM算法和SC-RANSAC算法能够100%获得成功匹配，而其余算法不能保证匹配成功.

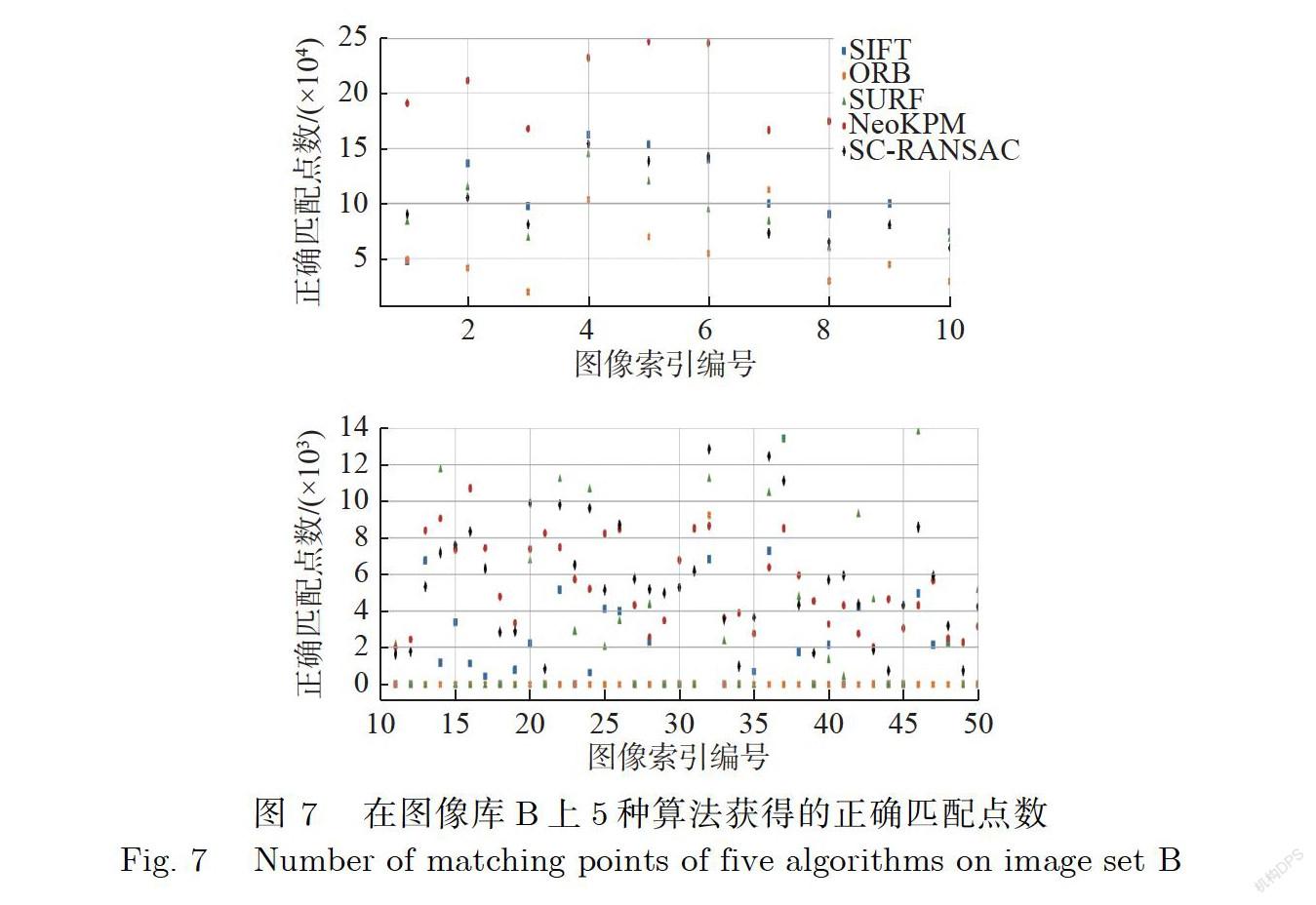
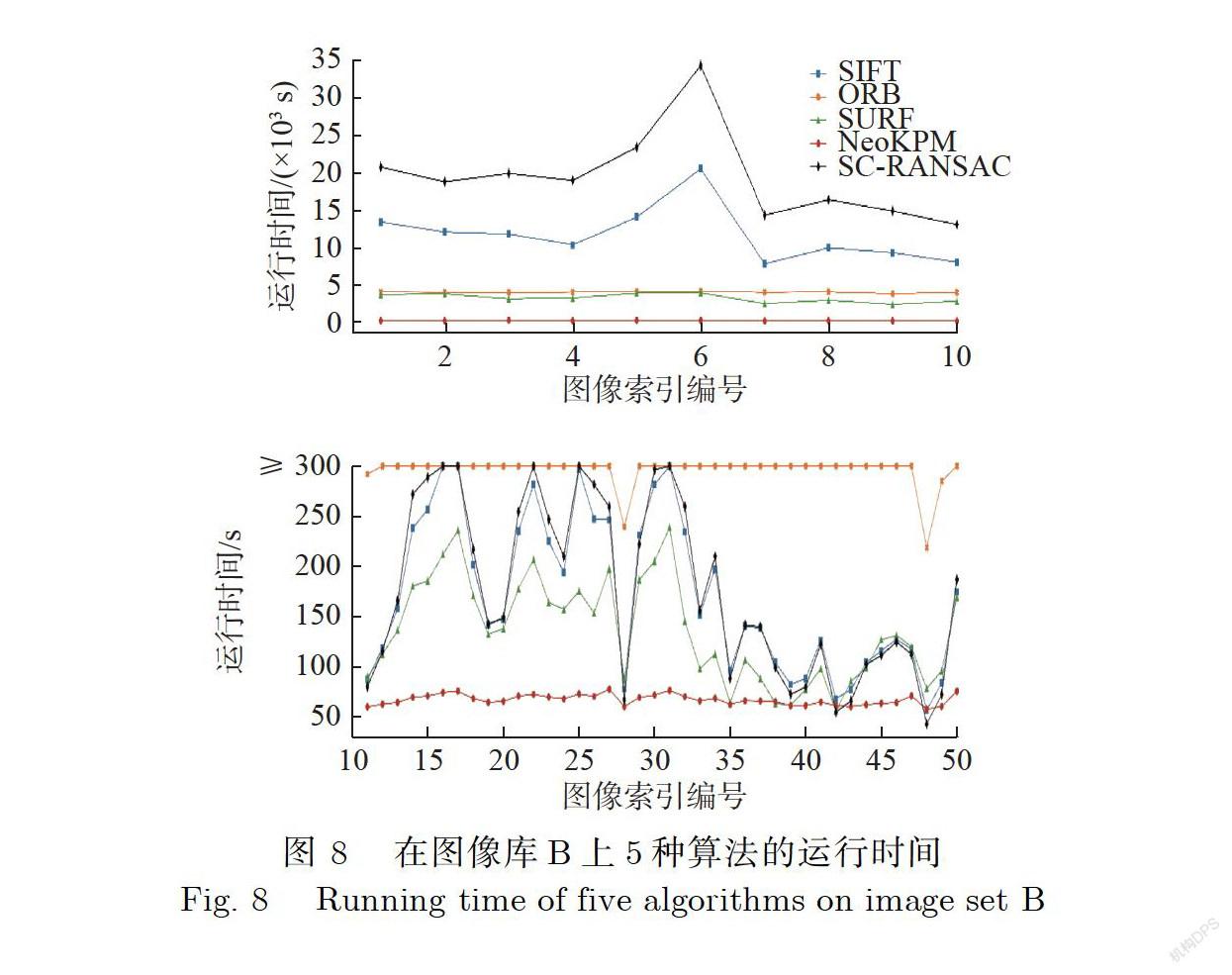
实验中，匹配成功所对应的匹配点被认为是正确匹配点，失败时匹配点数记为0.在图像库B上的5种算法的正确匹配点数和运行时间分别如图7和图8所示，其中横轴为图像库B中图像对的图像索引编号.由图7和图8可知，在纹理较为丰富、分辨率较高（（10288×7730）像素）的壁画图像上，NeoKPM算法的运行时间最少而匹配点数最多，其匹配点数要高出其余4种算法近1倍;在分辨率较低（（5087×3703）像素）的壁画图像上，NeoKPM算法相较于SIFT算法、ORB算法、SURF算法这3种经典算法，即使在图像重叠率不是很高的情况下也成功完成了所有的匹配任务;相比于同样完成全部匹配的SC-RANSAC算法，其平均匹配点数为7 577，高于SC-RANSAC算法的5 459.另外，如表8所示，NeoKPM算法的平均处理时间也远低于其他4种算法.

下面从图像库B里选两对重叠图像来观察图像在特征匹配后进行对齐处理的实际效果.图9（a）是来自图像库B的2幅有重叠的壁画图像，分别用SIFT算法、SC-RANSAC算法和NeoKPM算法对图9（a）进行特征点匹配处理后再进行图像对齐拼接处理，其拼接结果分别如图9（b）、图9（d）和图9（1）所示.为了方便比较，把左侧红色矩形区域进行放大后的局部图像放在其右边，如图9（c）、图9（e）、图9（g）所示.从图9（c）、图9（e）、图9（g）可以看到，SIFT算法和SC-RANSAC算法都有明显错位的纹理，而NeoKPM算法没有明显错位的地方.

图10（a）也是来自图像库B的2幅有重叠的壁画图像.分别用SC-RANSAC算法和NeoKPM算法对图10（a）进行特征点匹配处理后再进行图像对齐拼接处理，其拼接结果分别如图10（b）、图10（d）所示.图10（c）、图10（e）为把左侧红色矩形区域进行放大后的局部图像.由图10（c）、图10（e）可知，NeoKPM算法可以精确地对齐所有结构区域，但SC-RANSAC算法会错位纹理区域.

2.3NeoKPM算法与CODE算法的性能比较

CODE（Coherence based DEcision boundaries）[18]算法为近年来一种较为优秀的特征匹配算法，但由于其采用A-SIFT[21]来检测特征点，所以该算法只能处理最大为（640×480）像素的图像.为了与CODE算法进行比较，本文特地制作了分辨率为（640×480）像素的图像库C（参见2.1节图像库说明）.

在圖像库C上，对CODE算法和NeoKPM算法进行特征匹配处理的比较实验，实验结果如图11和图12所示，其中横轴为图像库C中图像对的图像索引编号，纵轴分别为这两种算法的特征匹配点的双向平均误差和运行处理时间.从图11可知，NeoKPM算法的匹配点平均双向误差约为0.30像素，而CODE算法的平均双向误差约为0.21像素，CODE算法比NeoKPM算法要好，但差别微小.从图12可知，NeoKPM算法的平均处理时间约为2.26s，CODE算法的平均处理时间约为5.04s，即使在这么小尺寸的图像上，NeoKPM算法的速度都比CODE算法要快近50%;相比于CODE算法，NeoKPM算法对被处理的图像没有大小的限制，且能够以较低的时间损耗完成高分辨图像的高质量匹配，匹配精度逼近CODE算法.

3结论

针对既有特征点匹配算法不适合高分辨率壁画图像的问题，本文提出了一种解决高分辨率壁画图像匹配的高速算法NeoKPM，该算法的主要特点如下：①针对具有高分辨率的壁画图像，采取降采样策略;②根据先验知识估算目标图像相对于参考图像的平移量，减少了特征匹配的搜索空间，在降低了计算复杂度的同时也提高了匹配的正确率;③从降采样图像的特征点计算出原图像的单应变换矩阵，极大地提高了原图像的特征点匹配的效率;④提出了基于灰度和颜色不变量的联合SIFT特征向量，解决了SIFT算法不能识别具有相同纹理不同颜色区域的问题.在实际壁画图像库上，本文对NeoKPM算法的性能进行了实验，实验结果表明：在分辨率为8000万像素的壁画图像上，本文算法每对图像的正确匹配点数量平均比SIFT算法高出近10万个，其特征点匹配处理速度是SIFT算法的20倍，其基于图像单个像素的双图像平均误差小于0.04像素.

本文所提出的NeoKPM算法是针对于高分辨图像提出的，其在低分辨率图像上的效果并不明显;同时如果在低分辨率图像上进行降采样处理，过少的特征点也将难以支持计算出一个相对准确的初始对应关系.根据壁画图像的拍摄方式和匹配精度的需要，本文算法主要支持两图像重叠率不低于20%的精准匹配.目前本文算法是在CPU上实现的，为了进一步提高处理速度，如何将本算法推导到并行算法并在GPU上进行实现是今后的课题.

致谢上海商务数码图像技术有限公司对本文的研究工作，不仅提供了全额资金支持，还提供了洞窟壁画图像供实验之用，在此表示衷心的感谢.

[参考文献]

[1]中华人民共和国国家文物局.古建筑壁画数字化测绘技术规程：WW/T 0082—2017 [S].北京：文物出版社，2017.

[2]LOWE D G. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision，2004，60（2）：91- 110.

[3]MATAS J，CHUM O，URBAN M，et al. Robust wide-baseline stereo from maximally stable extremal regions [J]. Image and VisionComputing，2004，22（10）：761-767.

[4]BAY H，ESS A，TUYTELAARS T，et al. Speeded-up robust features （SURF）[J]. Computer Vision and Image Understanding，2008，110（3）：346-359.

[5]RUBLEE E，RABAUD V，KONOLIGE K，et al. ORB：An efficient alternative to SIFT or SURF [C]// 2011 International Conference on Computer Vision. IEEE，2011：2564-2571.

[6]MUKHERJEE D，WU Q M J，WANG G H. A comparative experimental study of image feature detectors and descriptors [J]. Machine Vision and Applications，2015，26（4）：443-466.

[7]ABDEL-HAKIM A E，FARAG A A. CSIFT：A SIFT descriptor with color invariant characteristics [C]// 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR'06）. IEEE，2006：1978-1983.

[8]GEUSEBROEK J M，VAN DEN BOOMGAARD R，SMEULDERS A W M，et al. Color invariance [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23（12）：1338-1350.

[9]ALCANTARILLA P F，BARTOLI A，DAVISON A J. KAZE features [C]// Computer Vision-ECCV 2012，ECCV 2012，Lecture Notes in Computer Science. Berlin：Springer-Verlag，2012：214-227.

[10]ALCANTARILLA P F，NUEVO J，BARTOLI A. Fast explicit diffusion for accelerated features in nonlinear scale spaces [C]// Proceedings of British Machine Vision Conference. BMVC，2013：13.1-13.11.

[11]CHO Y J，KIM D，SAEED S，et al. Keypoint detection using higher order Laplacian of Gaussian [J]. IEEE Access，2020（8）：10416- 10425.

[12]SAVINOV N，SEKI A，LADICKY L，et al. Quad-networks：Unsupervised learning to rank for interest point detection [C]//2017IEEE Conference on Computer Vision and Pattern Recognition （CVPR）. IEEE，2017：3929-3937.

[13]DE TONE D，MALISIEWICZ T，RABINOVICH A. SuperPoint：Self-supervised interest point detection and description [C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops （CVPRW）. IEEE，2018：337-349.

[14]ONO Y，TRULLS E，FUA P，et al. LF-Net：Learning local features from images [C]// 32nd Conference on Neural Information Processing Systems （NIPS 2018）. 2018：6234-6244.

[15]FISCHLER M A，BOLLES R C. Random sample consensus：A paradigm for model fitting with applications to image analysis and automated cartography [J]. Communications of the ACM，1981，24（6）：381-395.

[16]ROUSSEEUW P J. Least median of squares regression [J]. Journal of the American Statistical Association，1984，79（388）：871-880.

[17]FOTOUHI M，HEKMATIAN H，KASHANLNEZHAD M A，et al. SC-RANSAC：Spatial consistency on RANSAC [J]. MultimediaTools and Applications，2019，78（7）：9429-9461.

[18]LIN W Y，WANG F，CHENG M M，et al. CODE：Coherence based decision boundaries for feature correspondence [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2018，40（1）：34-47.

[19]CHOU C C，SEO Y W，WANG C C. A two-stage sampling for robust feature matching [J]. Journal of Field Robotics，2018，35：779- 801.

[20]HARTLEY R，ZISSERMAN A. Multiple View Geometry in Computer Vision [M]. 2nd ed. New York：Cambridge University Press，2003.

[21]MOREL J M，YU G S. ASIFT：A new framework for fully affine invariant image comparison [J]. SIAM Journal on Imaging Sciences，2009，2（2）：438-469.

（責任编辑：李艺）