充满“威力”的比

黄旭军

学校最近重新分配了清洁包干区，一班和二班一起打扫700平方米的操场，相关负责人从操场中間把操场平均分给了两个班。

“可是我们班只有30人，他们班有40人，这太不公平了！”一班的劳动委员生气地和阿木老师说。

阿木老师居然笑了：“等这节课讲完‘用比例解题，我们就可以向相关负责人反映一下这个情况了。”同学们一下子来了兴趣。

阿木老师说：“如果将操场按300平方米和400平方米分配给一班和二班，你们觉得合理吗？”“合理！”同学们齐声喊道。

“这里就运用了比的知识。两个数相除又叫这两个数的比。因为人数比是30∶40，面积比是300∶400，化简后都是3∶4，所以你们觉得很合理。运用比解决问题，可能有意想不到的好效果！”

例1

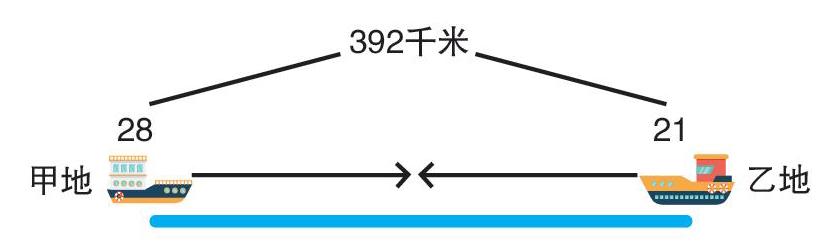
甲地到乙地的水上航行路线长392千米，同时从两地各开出一艘轮船，相对而行。从甲地开出的船每小时行28千米，从乙地开出的船每小时行21千米，两船相遇点与甲地的距离是多少？

相遇问题，先画图分析：

两船的行驶时间相等，先求出相遇时间。

我们可以算出392÷（28+21）=8（小时），经过8小时两船相遇。

如上图，求两船相遇点离甲地多远，实际就是甲地开出的船行驶的路程。它的速度是28千米/时，行驶了8小时，行驶的路程就是28×8=224（千米）。

观察上图，因为时间相同，所以速度快的船行驶的路程就多，速度慢的船行驶的路程就少，速度比就是路程比，28∶21=4∶3。

所以两船的路程比就是4∶3。将整段路程分成7份，所求的路程占4份，也就是392÷7×4=224（千米）。

答：两船相遇点与甲地的距离是224千米。

两位商人共带245枚鸡蛋去市场摆摊，一位商人的鸡蛋多，一位商人的鸡蛋少，但二人卖完鸡蛋得到的钱同样多。

一位商人说：“如果我有你那么多的鸡蛋，我能卖32元。”另一位商人说：“如果我有你那么多的鸡蛋，我只能卖18元。”那么，两位商人中所带鸡蛋较少的那位一共带了几枚鸡蛋？

两人按自己的价格卖完鸡蛋，得到的钱一样多。

根据最后所得的钱一样，我们可以列出方程。

解：设所带鸡蛋较少的商人带了x枚鸡蛋，每枚鸡蛋的售价为32

245-x元，另一位商人带了（245-x）枚鸡蛋，每枚鸡蛋的售价为18

x元。

根据题意列出方程：

x×32

245-x=（245-x）×18

x，解得x=105。

为了便于说明，把多的那份鸡蛋的数量设为A，价格设为B。把少的那份鸡蛋的数量设为C，价格设为D。根据比，我们可以得到：32=A×D，18=B×C。

因为两份鸡蛋卖的钱一样多，所以有AB=CD，可以推导出D=AB

C。由此可

得A×D∶B×C=32∶18，再将D=AB

C代入，可得A×A∶C×C=32∶18=16∶9，A∶C=4∶3。

两位商人的鸡蛋数量比是4∶3，少的那份鸡蛋的数量是245÷7×3=105（枚）。

答：在两位商人中，所带鸡蛋较少的那位一共带了105枚鸡蛋。

训练一二一

甲和乙一起做300个零件，甲7小时可以做500个，乙7小时可以做250个，两人同时开始，同时完工，完工时两人各做了几个零件？（答案见下期）