惯性测量系统火箭橇试验一维运动约束方法

魏宗康，高荣荣

（北京航天控制仪器研究所，北京，100854）

0 引 言

火箭橇是利用火箭发动机作动力在特定轨道上模拟载体实际飞行的大过载、高强度、强振动和冲击等力学环境的设备。惯性测量系统火箭橇试验通过采用精确的时间、速度和位置等测试手段，以验证惯性测量系统的精度，或分离大过载下的惯性器件高阶误差[1,2]。

在利用火箭橇试验对惯性测量系统进行性能和精度评估时，主要是根据火箭橇在直线轨道上的单方向一维运动特点。文献[1]给出了一种过载曲线设计，给出了在轨道长度限制条件下在主动段、自由滑行段和制动段的时变过载值。文献[2]给出了火箭橇试验时的振动传递特性。

在分离惯性测量系统的误差时，主要采用导航位置与外测位置进行比较[3,4]。但由于导航位置是三维的，而外测位置只是一维的，这就面临着如何把三维导航位置折算到一维轨道运动方向上的问题。文献[5]中给出了一种分离惯性测量系统误差系数的火箭橇试验方法，给出了对导航位置一维化的近似处理，主要是只考虑运动方向X 轴加速度计，而忽略了其它两轴（侧向Y 轴和高度方向Z 轴）的误差项，但是这种处理存在着很大的方法误差。如果Y 轴和Z 轴的导航位置误差为有用信息时，则只利用X 轴位置误差序列值分离的加速度计误差系数与真实值存在着较大的偏差，甚至导致不正确的结论[6]。

事实上，火箭橇只在其运行方向上存在位置和速度误差，即在与运行方向垂直的另外两个方向上的速度和位置均为零。但是，在实际火箭橇试验的导航解算中其它两个方向存在着非零误差，分析原因主要是由于惯性测量系统在橇体上的安装误差、导航初始对准误差和姿态误差等因素造成的。为解决上述问题，本文提出了一种惯性测量系统火箭橇试验一维运动约束方法。利用开环卡尔曼滤波器来开环估计橇体的姿态误差角，并补偿其对橇体运行方向上的影响，最终将火箭橇的三维运动简化为精确的一维运动。只有在一维运动的情况下才能分离出惯性测量系统的误差系数。

1 火箭橇试验橇体运动一维化必要性分析

惯性测量系统火箭橇试验过程中，火箭橇的运动为标准的一维直线运动，即橇体在滑轨的侧向和高度方向上的速度和位移均为零。而在实际导航解算的结果中，由于初始对准误差、仪表误差和其他外界因素的干扰，火箭橇的运动轨迹并非理想的一维直线，而属于三维轨迹[7]。

惯性测量系统基于发射点轨道坐标系的一次导航结果如图1 所示。

图1 惯性测量系统火箭橇试验导航结果Fig.1 Navigation Result of Rocket Sled Testing of Inertial Testing System

惯性测量系统火箭橇试验过程中，Y 轴和Z 轴的位移应为0，但导航解算后的位移和速度都不为0，位移最大可达10 m。经过显著性分析，在Y 轴和Z 轴的位置误差主要是由于初始对准误差引起的，该项误差反映了初始对准的角度大小，为有用信息。如果按照文献[5]直接忽略Y 轴和Z 轴的位置误差进行误差分离将导致分离的误差系数有偏差，只考虑运行方向X 轴的位置误差如图2 所示，在图2 基础上进行误差分离将导致分离的误差系数有偏差。为此，需要研究一种将Y轴和Z 轴的位置误差折合到X 轴方向上的一维约束方法。

图2 惯性测量系统火箭橇试验X 轴导航位置及其误差Fig.2 Position and Position Error of X Axis of Rocket Sled Testing

2 火箭橇试验橇体运动一维化原理

为了减小X 方向上的非加速度计仪表误差因素，同时减小Y 轴和Z 轴的导航解算位移误差，应改善导航算法和提高导航。

橇体运动一维化的原理为：在橇体运行时，惯性测量系统通过基于轨道坐标系的导航算法求解得到3 个方向上的位置、速度和姿态角，利用Y 轴和Z轴方向上的位置真值和速度真值为0 来实时估计姿态角误差，并从X 轴方向上的位置和速度中扣除掉姿态角误差引起的分量[8～10]。

在橇体运行时，姿态误差方程写成分量形式为

式中 φx，φy，φz分别为橇体在X，Y，Z 方向上的姿态角；δφx，δφy，δφz分别为橇体在X，Y，Z 方向上的姿态角误差；ωx，ωy，ωz分别为橇体在X，Y，Z 方向上的角速度；分别为地球自转角速度相对于X，Y，Z 坐标轴的角速度在轨道坐标系下的分量；分别为地球自转角速度相对于X，Y，Z 坐标轴的角速度在地理坐标系下的分量。

由于Y，Z 方向的速度真值为零，因此Y，Z 方向的速度计算值等于速度误差值，得到的速度误差方程如下：

式中 vy，vz分别为橇体在Y，Z 方向上的速度计算值；δvy，δvz分别为橇体在Y，Z 方向上的速度误差值；ax，ay，az分别表示橇体在X，Y，Z 方向上的加速度。

位置误差方程为

式中 ry，rz分别表示橇体在Y，Z 方向上的位移。

因此，橇体运动一维化的基本思路就是，利用Y轴和Z 轴方向上的速度和位置来估计姿态角误差，再把姿态角误差折合到X 轴进行修正和补偿的过程。

另外，橇体导航过程有两个阶段：第1 阶段为橇体从发射时刻到停止时刻的运行段；第2 阶段为橇体停止后的静止段。在这两个阶段的一维化处理方法不同，所以，橇体运动一维化也应该分运行段和静止段。

3 火箭橇运行时的姿态角误差估计的可观测性分析

针对第1 节提出的火箭橇试验橇体运动一维化处理的必要性问题，本节提出一种开环估计和补偿的方法，可消除Y 轴和Z 轴的位置误差，使得两个轴的位移始终近似为0，则橇体在三维空间的运动可简化为一维的直线运动。

3.1 估计姿态角误差的状态方程和观测方程

设状态变量为 vy，ry，vz，rz，δφx，δφy和δφz，有7 维状态方程：

式中

观测方程为

3.2 橇体运行时估计姿态角误差的可观测性分析

在分析可观测性时，为分析方便，定义分块矩阵：

在一个导航周期内各元素可看作常值，对于线性定常连续系统有可观性矩阵：

对Q 进行初等行变换，有：

忽略小量，有：

在式（10）中前两行各元素只取决于3 个方向的加速度，后两行除加速度外，还取决于橇体运行的角速度和地球转速。由于地球转速对可观测性分析的影响可以忽略不计，因此，上式可进一步简化为

式（11）决定了系统是否完全可观测。在进行火箭橇试验时，由于运行方向过载ax较大，ay和az相对较小，如果只根据前两行则不能判断δφx能否完全辨识出来。第3 行没有参考价值，而根据第4 行可给出δφx能否完全辨识出来的两种情况。

第1 种情况是 ωz≈0，此时 axgωz≈ aygωz≈0，都为小量，因此，辨识出来的δφx置信度较低。第2 种情况是ωz值较大，此时 axgωz＞ aygωz，因此，辨识出来的δφx置信度较高，且其可观测性随着ωz值由大到小逐渐变弱。即：

在橇体运行时方位角的变化近似为0，因此可设ωz=0，如果在误差辨识时继续采用以上7 阶误差模型，则辨识出的δφx置信度较低或不可观测。因此可采用模型降阶。令δφx=0，将7 阶姿态角误差模型降为6 阶，可观测性分析方法与7 阶模型相同。因此，系统完全可观测的充要条件是，忽略小量，即式（11）的第1 列，由可观测性矩阵得到：

在式（13）中前两行各元素只取决于X 轴方向的加速度，后两行除加速度外，还取决于橇体运行的角速度和地球转速。在火箭橇试验时，由于运行方向过载ax较大，只根据前两行即可将δφy和δφz完全辨识出来，因此，6 阶系统完全可观。

4 火箭橇停止时的姿态角误差估计

由于方位角不完全可观，当火箭橇停止时，令δφz=0，则姿态误差方程写成分量形式为

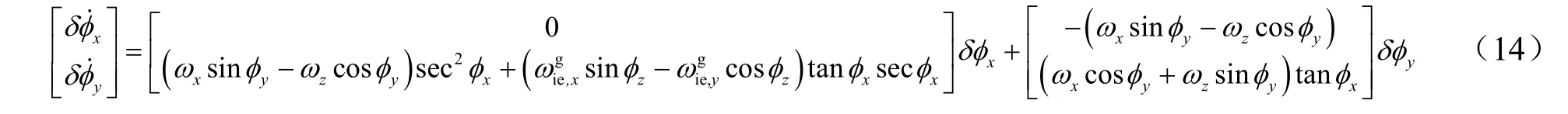
另外，忽略天向通道后的速度误差方程为

忽略天向通道的位置误差方程为

设状态变量为vy，ry，δvx，δrx，δφx，δφy，有状态方程：

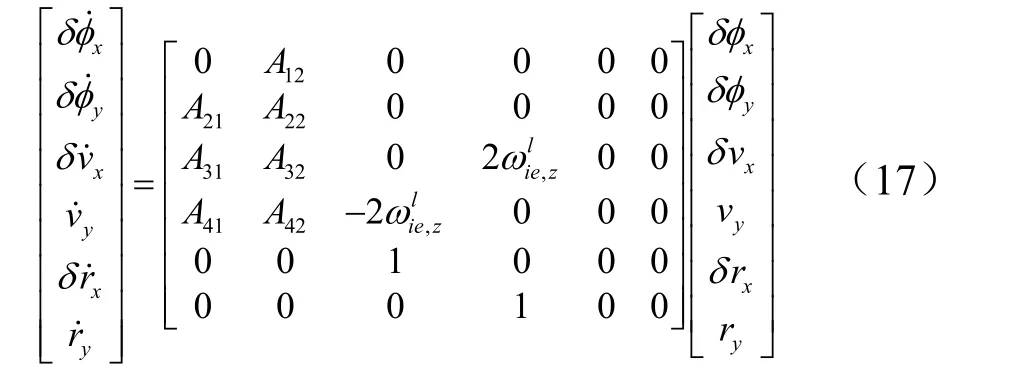
式中

观测方程为

当火箭橇停止运行时，用3.2 小节相同的方法对其状态方程和观测方程进行可观测性分析，可知其观测性矩阵为满秩，系统完全可观。

5 橇体姿态角误差的开环估计和补偿方法

下面利用开环卡尔曼滤波器来开环估计δφy和δφz，并实时补偿其对X 轴橇体运行方向上的影响。所谓实时开环修正，就是利用卡尔曼滤波器对导航误差的姿态角估计值，在导航过程中只对X 轴加速度、速度和位置进行开环修正。

在火箭橇系统运行时，利用卡尔曼滤波器对导航误差进行实时估计，但不修正各项误差，工作原理如图3 所示。

图3 火箭橇运行中开环估计流程Fig.3 Diagram of Open-loop Estimation During the Rocket Sled Test Running

在火箭橇系统停止时，利用零速修正原理来求解两个水平姿态角，工作原理如图4 所示。

图4 火箭橇停止后开环估计流程Fig.4 Diagram of Open-loop Estimation after the Rocket Sled Test Stop

利用式（20）对导航算法中速度实时补偿过程为

6 仿真试验验证

下面给出卡尔曼滤波器对姿态角、速度误差和位移误差的估计结果及经过开环补偿之后的导航结果。

以图1 实际试验导航数据为例，取卡尔曼滤波器I 的初始参数P0=I7，Q0=1×10-9I7，R0=1×106I4，用开环卡尔曼滤波器对7 个误差项vy，vz，ry，rz，δφx，δφy和δφz进行估计，姿态角误差见图5，速度和位移误差见图6。

把估计的3 个姿态角误差δφx，δφy和δφz重新代入式（21）的补偿公式后进行导航解算，结果如图7 所示。从导航结果可以看出，Y 轴和Z 轴的位移误差已减小到1 cm 左右。

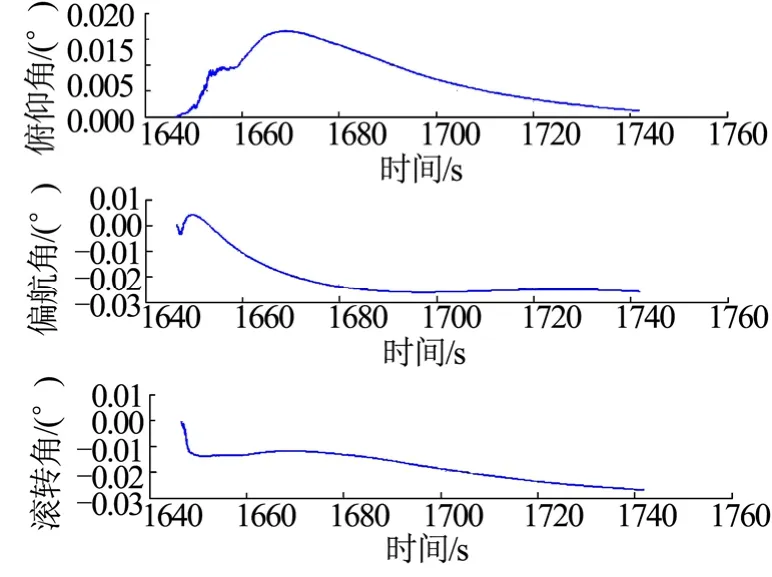
图5 运行段姿态角误差的估计结果Fig.5 Estimation of Attitude Angle Error During the Rocket Sled Test Running

图6 速度和位移误差的估计结果Fig.6 Estimation of Velocity Error and Position Error

图7 经过误差开环补偿后的导航结果Fig.7 Navigation Result after Open-loop Compensation

图7 中与X 轴运动有关的遥外测误差如图8 所示。

图8 经过误差补偿后的遥外测误差导航结果Fig.8 Position and Position Error of X Axis after Error Compensation

比较图2 和图8 可以看出，X轴位置误差明显不同，图2 是直接忽略了Y 轴和Z 轴的误差，而图8 是经过本文介绍的一维运动约束后的结果。在后续误差分离时，应以图8 的结果为准。

总之，通过以上基于开环估计和实时补偿的过程，把惯性测量系统火箭橇试验时的三维运动简化为一维直线运动。此时，Y 轴和Z 轴的线位移近似于0，只需考虑X 轴方向上的运动即可。

7 结 论

由于惯性测量系统在橇体上的安装误差、导航初始对准误差和姿态角误差等因素的影响，造成火箭橇运动在侧向Y 轴和高度方向Z 轴上的速度和位移均不为零，从而导致导航解算后的X 方向上的运动并非精确的一维直线运动。

为此本文提出了一种惯性测量系统火箭橇试验一维运动约束方法。利用卡尔曼滤波器对火箭橇姿态角误差、速度误差和位移误差状态量进行开环估计，并利用Y 轴和Z 轴上速度和位移误差为零原理进行误差修正补偿，使得橇体在Y 轴和Z 轴上的位置和速度近似为零，最终将火箭橇的三维运动简化为精确的一维直线运动。通过试验验证，经过卡尔曼滤波估计和零速修正补偿后的Y 轴和Z 轴的位移误差已减小到1 cm左右，近似为0，实现了火箭橇试验运动一维化的处理。