一类带参数积分中值公式的证明
吴定能
(贵州电子信息职业技术学院,贵州 凯里 556000)
积分中值定理是积分学的重要内容,也是一直以来研究的热点课题。以前大多是集中于研究它的推广与深化。目前,研究出不同类型的积分中值公式已成为中值定理研究的重点课题。本文在总结了微积分的理论之后,对带参数积分建立了一类带参数的积分中值定理,并且完成了证明。
1 带参数积分中值公式一
(1)
证明:证明分三步完成。
1)当n=1时,我们直接计算
从而,若ρ≠0且ρ∈(-1,1)时,我们有
(2)
很显然,当ρ=0时,恒等式(2)也成立。
2)当n=2时,利用分部积分公式直接计算,可得
(3)
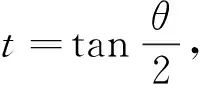
于是
(4)
结合(4)及(3)可以得到
因此,若ρ≠0且ρ∈(-1,1)时,可得到
(5)
此外,很显然,当ρ=0时,恒等式(5)也成立。
这意味着恒等式(1)适用于n=1或n=2的情况。
3)为了证明一般性结论,让|ρ|<1,n≥3。一方面,利用分部积分公式,我们有
(6)
另一方面,将积分函数中分子sinnθ拆为sin2θsin2θ,可得到
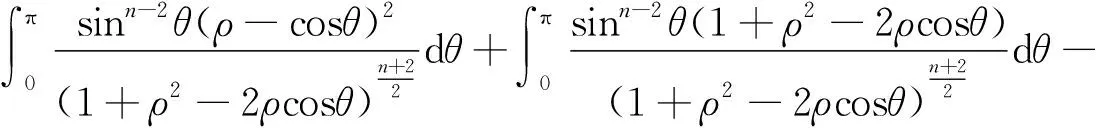
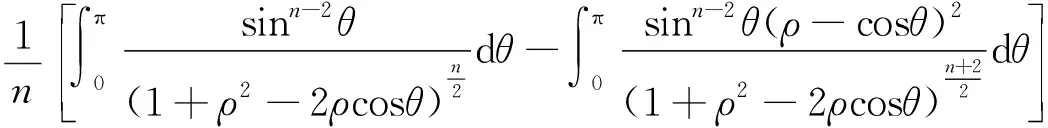

从而,可得到
(7)
结合恒等式(6)及(7)可得到
移项整理后,得到
(8)

由于fn(ρ)在区间(-1,1)连续,那么对恒等式(8),fn(ρ)满足微分方程
ρfn′(ρ)+(n-1)fn(ρ)=0
(9)
在ρ∈(-1,1),令Fn(ρ)=ρn-1fn(ρ)
那么Fn(0)=0,而且
Fn′(ρ)=(n-1)ρn-2fn(ρ)+ρn-1fn′(ρ)
=ρn-2[(n-1)fn(ρ)+ρfn′(ρ)]
进而,由微分方程(9),可以得到Fn′(ρ)=0,ρ∈(-1,1)。
从而,结合Fn(0)=0,得到Fn(ρ)=0,ρ∈(-1,1)。
因此,当ρ≠0时,一方面,可以得到fn(ρ)=0,ρ∈(-1,1)。
另一方面,根据fn(ρ)的定义可得fn(0)=0。
因此,可得
(10)
(11)
结合恒等式(6)
因此,当ρ≠0时,我们可以得到
(12)
此外,当ρ=0时,恒等式(12)也成立。
若m≥2,|ρ|<1时,对恒等式(12),可得到
当n为2m时,有
(13)
当n为2m-1时,有
(14)
结合恒等式(13)及(14),当n≥3,|ρ|<1时,我们可以推出恒等式(1)成立。再结合恒等式(2)及(3),可以得到,当n≥1,|ρ|<1,时,恒等式(1)恒成立。
2 带参数积分中值公式二

(15)
证明:证明分为五步完成
1)当n=1时,我们直接计算
因此,如果ρ≠0时,可以得
(16)
当ρ=0时,恒等式(16)显然成立。
2)当n=2时,我们直接计算
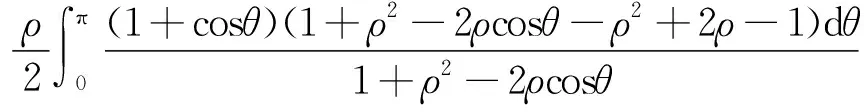

结合恒等式(4),可得到
因此,若ρ≠0时,可得
(17)
同时,也很显然,当ρ=0时,恒等式(17)也成立。这意味着恒等式(15)也适用于n=1或者n=2的情况。
3)当ρ=1时,利用二倍角公式,可以得到

(18)
4)当ρ=-1时,同理,根据二倍角公式,可以得到

(19)
由恒等式(18)及(19),我们可以立即得到

这意味着恒等式(15)也适用于|ρ|=1的情况[2]。
5)为了证明一般性,假设|ρ|<1,n≥3时,根据fn(ρ)=0,可以得到
结合恒等式(1),可以得到
(20)
因此,由恒等式(17)、(18)、(19)及(20)可以得出,对于n≥1且|ρ|≤1时,等式(15)恒成立。
3 带参数积分中值公式三
(21)
证明:证明分为两步完成。
1)当n=2时,等式(21)显然成立。
2)为了证明一般性,当n≥3,|ρ|≤1时,利用恒等式(21),替换n(n+2→n),可直接得到
再结合恒等式(15),可以得到
因此,可以得到
(22)
从而,当n≥3,|ρ|≤1时,恒等式(21)成立。
因此,由(1)和(2),我们可以得到,当n≥2且|ρ|≤1时,恒等式(21)恒成立。

