用尖点突变理论研究疲劳断裂事故
(中国电子科技集团公司第七研究所,广东广州 510310)
1 机械疲劳断裂过程
疲劳断裂是一种常见的破坏现象,疲劳断裂发生时有以下几点特点:第一,疲劳断裂前零件不产生明显的变形,突然发生断裂。第二,零件破坏时的工作应力远低于材料的抗拉强度,甚至低于材料的屈服极限。第三,断口从宏观来看由两个区域构成,即金属颗粒细、光亮的带有疲劳线的疲劳裂纹扩展区和金属颗粒组大的瞬时断裂区。
疲劳断裂需要经过三个阶段,即微裂纹产生阶段、疲劳裂纹扩展阶段、断裂。这样一个过程也可以理解为加载受力后,材料疲劳磨损程度慢慢增加(微裂纹产生阶段)经过一个相对稳定的增加期后,机械疲劳磨损量开始出现加速增加(疲劳裂纹扩展阶段),机械磨损量一次次的增加,当接近材料寿命时,以前载荷作用对材料强度影响的累积效果,加上最后一次对材料强度性能的加剧恶化超过材料固有的承受界限,机械系统将发生瞬时断裂(突变)。发生突变时的损伤值也就是系统的临界损伤量。疲劳的最终结果是瞬间断裂,实际上该过程其实是一个逐渐失效的非线性变化过程,该过程可用突变理论解释。为了更加系统地研究该过程,了解临界损伤量的数值,本文以突变理论为基础,对疲劳断裂过程进行分析和研究。
2 突变理论及突变类型
1972年法国数学家雷内·托姆在《结构稳定性和形态发生学》一书中明确地阐明了突变理论。突变理论研究的是从一种稳定组态跃迁到另一种稳定组态的现象和规律。它指出自然界或人类社会中任何一种运动状态都有稳定态和非稳定态之分。在微小的偶然扰动因素作用下,仍然能够保持原来状态的是稳定态,而一旦受到微扰就迅速离开原来状态的则是非稳定态,稳定态与非稳定态相互交错。它提供了一种研究有跃进、不连续和突然质变的数学方法,突变理论涉及拓扑学、分叉理论、起点理论等许多理论,但是它以两点为假设前提[1]:
(1)假定系统在任何时候的状态可以由给定的n个变量系统受到m个(u1,u2,…um)独立变量的控制,即这些变量的值决定了xi的值,并把xi叫做状态变量,ui叫做控制变量。(2)系统的动力学可以由一个光滑的势导出。
突变理论告诉我们,突变类型的数目不取决于状态变量的数目,当控制参数不大于4个时,只有7种不同类型的突变,如表1所示。
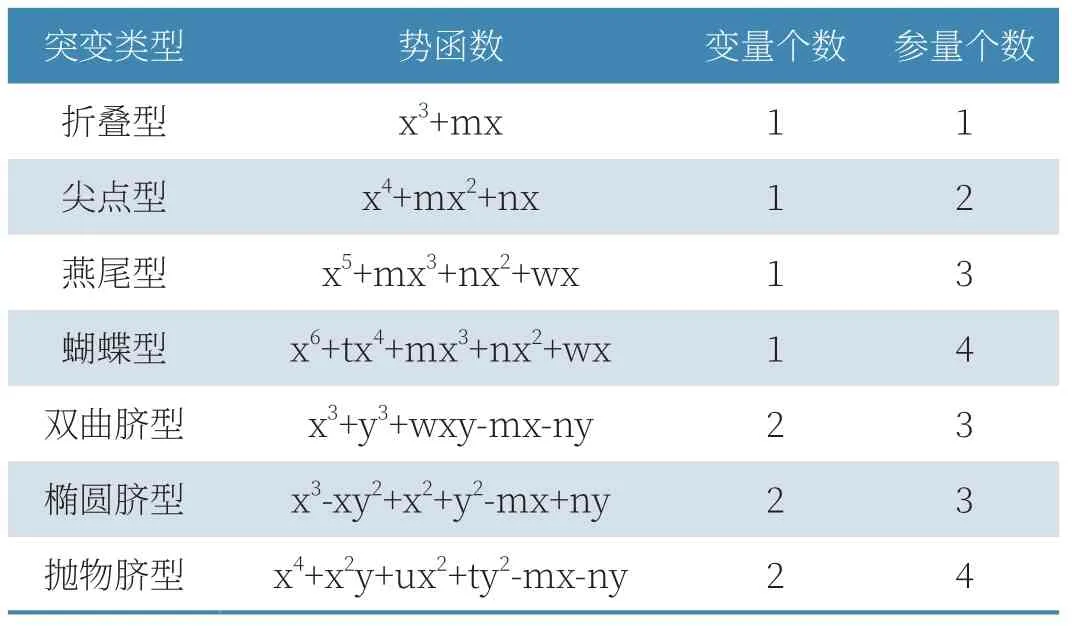
表1 突变类型
3 疲劳断裂事故的突变过程及特性
如图1所示,建立疲劳断裂突变模型,该模型具有折叠翼的平面曲线,由2个控制变量m、n(平面坐标,m和n分别表示工作应力和材料动力学特性)和状态变量x(x表示裂纹长度,垂直坐标)构成的三维系统,模型分为上、中、下三叶,下叶和上叶都是稳定结构,分别表示了疲劳断裂发生前和发生后的两种稳定结构,中间叶是不稳定的失稳突变,疲劳断裂过程可以描述为:系统从B点出发沿轨迹向A点逐渐演化,当接近折叠翼边缘时,只要系统状态量x有微小变化,系统陡然间从下叶突跃到上叶,在实践中表现为当接近材料寿命时,以前载荷对材料强度影响累积,加上最后一次对材料强度性能的加剧恶化造成了断裂表面瞬时增加,而材料的剩余界面很少,无法承受外加载荷而发生断裂失稳。这一过程表现出了明显的突变特点:
(1)多模态特征,即上下两叶机械系统状态不同;(2)突变特征,即经过折叠曲线时发生突变,瞬间断裂;(3)发散特征,即系统状态量x有微小变化导致状态完全不同;(4)不可达特征,即实际上系统不可能达到中间状态。
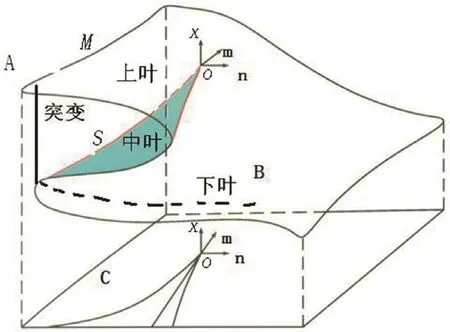
图1 疲劳断裂突变模型
4 机械疲劳断裂事故发生的充分必要判据和条件
尖点突变的势函数为:

由疲劳断裂突变模型知,系统是由状态变量x和2个控制变量构成的三维系统,其曲面平衡方程为:
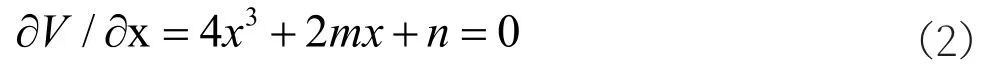
把平滑函数的位势导数为0的点称之为定态点,而在某些定态点附近连续变化引起不连续变化的结果,将这些退化的定态点称为奇点,故奇点集需要满足:

公式(2)和(3)联立后消去x可以得到疲劳断裂分叉集方程为:

公式(4)就是疲劳断裂事故发生的充分必要判据,可以作为疲劳断裂突变演化状态与临界失稳状态的距离。随着状态量的不断变化,当D=0时,状态变量发生突变从而导致疲劳断裂。
樊世清[2]等人对系统在疲劳断裂过程中的变化情况作了深入研究,材料发生尖点突变的条件是试验机主轴的刚度等于或小于试样瞬时有效刚度与一个常数乘积的绝对值,即k≦|k*e-2|,其中k是试验机主轴的刚度,而在断裂的临界状态时,由材料的原始特性和应力水平及疲劳损伤程度所决定。
5 机械疲劳断裂过程的预防措施
机械疲劳的断裂过程其实是一个非线性的变化过程,为了防止该类事故的发生关键在于能够在微裂纹产生阶段采取措施,防止疲劳区域的扩大,因为一旦扩大到疲劳裂纹扩展阶段,将出现加速磨损的过程。为了降低应力集中应该在设计和加工阶段阶段做到如[3]:
(1)在设计阶段。尽量避免尖角、缺口和截面突变,尽可能的平滑和均匀;尽可能地增大过渡处的圆角半径;在不可避免要产生较大应力集中的结构处可采用减荷槽来降低应力集中的作用。(2)在加工阶段。降低表面粗糙度,提高加工质量,提高疲劳极限;减少表面的氧化、裂纹、脱碳等表面缺陷。
6 结论
(1)机械疲劳的最终结果是瞬间断裂,但是实际上该过程其实是一个逐渐失效的非线性的变化过程,该过程可用尖点突变理论解释。(2)建立了机械疲劳断裂突变模型,该模型是具有折叠翼的平面曲线,当接近折叠翼边缘时,只要系统状态量x(位移值)有微小变化,系统陡然间从下叶突跃到上叶,发生突变,断裂发生。(3)随着状态量的不断变化,当D=0时,状态变量发生突变从而导致疲劳断裂。机械疲劳断裂分叉集方程为:结构和尺寸的突变是应力集中的机构根源,为了预防此类事故,关键是在微裂纹产生前采取措施,防止应力集中。

