基于万有引力算法的混沌图像加密研究

张毅 王波

摘要：网络科技的发展使得信息安全问题越来越尖锐，信息加密的研究已经提上议程。混沌密码学的新兴使得信息加密的安全性得到了有力支撑。该文就此提出基于万有引力算法的混沌图像加密方案，该算法利用五维分数阶混沌动系统生成的时间序列与像素置乱以及万有引力算法扩散后的图像再次进行扩散，形成加密图像，由于分数阶混沌系统具有初值敏感性、记忆性等优良特性以及万有引力算法的像素联合性，使得加密后的图像具有良好的抗攻击能力。

关键词：分数阶超混沌系统;万有引力算法;记忆性

中图分类号：TP309.7        文献标识码：A

文章编号：1009-3044（2020）30-0001-05

开放科学（资源服务）标识码（OSID）：

Abstract： The development of network technology makes the problem of information security more and more acute. The security of information encryption is strongly supported by the new development of chaos cryptography. In the image encryption scheme based on gravity algorithm is put forward， the algorithm using 5 d fractional order chaotic dynamic system to generate time series and pixel scrambling and diffusion： the image again after gravity algorithm， encryption image formation， because of the fractional order chaotic systems with initial value sensitivity， memory and other excellent properties， and the algorithm of gravity pixel combination， make the encrypted image has a good ability against the attack.

Key words： fractional-order hyperchaotic system; gravitation algorithm; memory

自20世纪混沌学发展以来，由于混沌系统的不可预测性、初值敏感性、时间序列的伪随机性等多种优异的特点，深受广大学者的青睐，掀起了对混沌系统的研究，而混沌学与密码学的结合，使得传统密码学的发展得到了质的飞跃。混沌密码学结合了混沌学以及密码学各自的优点，使得混沌密码学拥有了高效的加密性能。近年来，基于混沌系统的各类加密算法应运而生，混沌密码学得到了快速的发展。基于混沌序列的图像加密研究是目前解决图像信息泄露的有效途径。

1 研究现状

20世纪90年代的图像加密是该领域的起步阶段，当时的图像加密是建立在低维混沌系统和经典的置乱算法的基础之上，加密算法简单，随着科技进步很多过往的算法已经不再适用，但前人的研究思想为后来的图像加密领域提供了宝贵的经验和指明了方向。广大学者在对数字图像安全问题的研究过程中根据其加密的不同原理提出了不计其数的方法[1-7]。文献[8-10]中Yen最先提出一种CKBA的加密模式。该算法首先利用混沌映射产生序列，然后对该序列按一定方法进行转化，使其作为图像加密序列，最后让该二进制序列与图像像素进行异或或者异或非操作，以此完成对图像信息进行加密。文献[11]中Scharinger提出一种基于柯儿莫哥洛夫流的加密方案。在该方案中，他把整个完整图像看成一個单独的部分，利用柯儿莫哥洛夫流的键控混沌系统进行排位。为了打乱原来数据，采用了移位寄存伪随机数生成器进行像素位置的变换，从而打乱密文图像的特性。文献[12]中Fridrich提出在一个环面上或一个正方形上应用可逆的二维混沌映射来创建新的对称块的加密方案。首先通过混沌映射引入参数进行广义化，然后离散到一个有限的正方形点阵中，这些点阵代表像素和其他一些数据项。最后利用离散映射和简单的扩散机制进行组合。文献[13-16]Zhang等人给出了一种新的基于DNA序列和混沌序列的图像加密方案。首先对初始图像进行编码得到DNA序列矩阵，然后把矩阵分成若干相等的部分，利用DNA序列加法运算将这些部分相加。接下来，使用两个逻辑映射对添加矩阵的结果执行DNA序列补体操作。之后通过第三步对DNA序列矩阵解码，实现图像加密。文献[17]Chapaneri等人提出了一个改进的CML （ICML）使用分段线性混沌映射代替逻辑映射，以实现更好的混沌特性。文献[18，19]Sun等人给出了一种基于空间混沌系统的图像加密新方法。该方案利用空间Cat映射来对像素进行位置洗牌，并利用另一个空间混沌系统来混淆密文图像与明文图像之间的联系。

本文提出基于万有引力算法的混沌图像加密方案，该算法利用分数阶混沌动系统生成的时间序列与像素置乱以及万有引力算法扩散后的图像再次进行扩散，形成加密图像，由于分数阶混沌系统具有初值敏感性、记忆性等优良特性，以及万有引力算法的像素联合性，使得加密后的图像具有良好的抗攻击能力。

2 算法描述

2.1 小波变换

小波分析是当今世界信息分析处理领域中一种重要的方式，目前已经被广泛应用于图像处理、图像加密上。将待处理图像通过小波变化得到低频、水平、垂直、对角系数图。选取高能量的低频子图进行后续处理。小波变换能提高图像加密的效率。原图Im如图1（a）所示。灰度降噪后的图像Im1如图1（b）所示。图1（c）给出的是Im1一次小波变换的过程。小波变化后低频、水平、垂直、对角分量如图1（d）～（g）所示。

2.2 分数阶混沌系统

作为混沌图像加密中最重要的组成部分，混沌系统的复杂情况会影响到信息加密的可靠性能的优劣。就此，本文介绍一种分数阶超混沌系统，该系统秉持了传统整数阶混沌系统的优秀特性，同时还拥有分数阶混沌系统特有的记忆特性，使得系统的结构更加复杂。分数阶超混沌系统的动力方程如下式（1）所示。

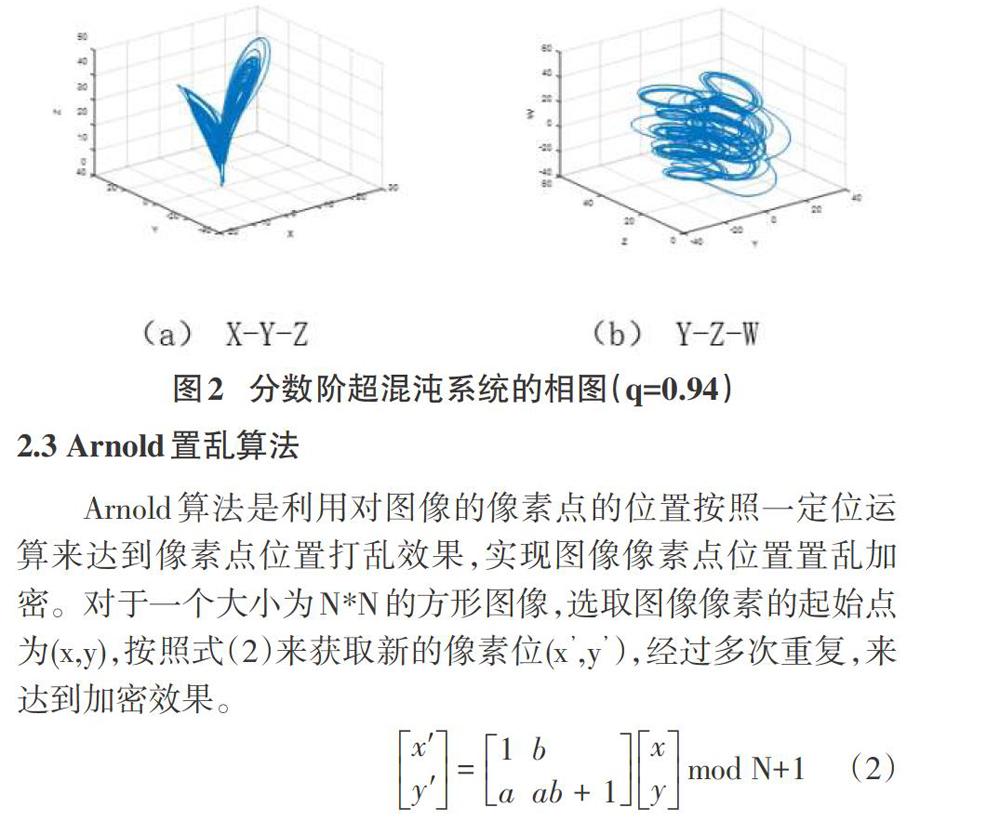
式（1）中a、b、c、d、e均为混沌系统参数，q是分数阶微分方程的阶次。实验仿真中选取系统参数值为a=10、b=28、c=8/3、d=0.1、e=0.2，分数阶微分方程的阶次q取值范围为（0.93，1），分数阶超混沌系统的系统参数对整个系统的变化有非常大的影响，决定着超混沌系统是否处于混沌状态还是其他状态。输入初值x0=0、y0=0.6、z0=0.3、w0=1、v0=1。根据选定的参数和初始值进行matlab仿真，得到分数阶超混沌系统的相图，如图2所示。

2.3 Arnold置乱算法

Arnold算法是利用对图像的像素点的位置按照一定位运算来达到像素点位置打乱效果，实现图像像素点位置置乱加密。对于一个大小为N*N的方形图像，选取图像像素的起始点为（x，y），按照式（2）来获取新的像素位（x，y），经过多次重复，来达到加密效果。

2.4 万有引力算法

2.4.1 万有引力算法介绍

十七世纪后半叶，英国著名物理学家牛顿首次在公开发表的期刊上提出万有引力定律。他认为在自然界中的任意两个有质量的物体都是彼此吸引的，小到尘埃，大到星体，而两者之间的引力作用的大小与该两个物体本身的质量以及两者之间的距离有关。万有引力定律的提出为了人类探索未知指明了一个方向。被认为是17世纪最伟大的发现之一。万有引力算法是根据牛顿万有引力定律改进而来，将物与物之间的引力作用映射到了图像像素点之间，通过图像像素点之间的引力作用计算引力大小，得到引力矩阵进行图像加密。

2.4.2 算法参数定义

将RGB图像放入X、Y、Z三维直角坐标中，对像素点之间的万有引力计算给出如下定义，使我们在空间中对RGB图像的像素点之间的万有引力计算提供便利，空间中的RGB图像像素点间的万有引力作用如图3所示。

定义1：像素点质量

引入像素点间的引力作用这个概念的前提是像素点是有质量的，文献[20]中通过像素点在空间中的位置关系引入像素点位置与质量关系式。同理，我们将该文献中空间中的一点扩展到图像的R、G、B三个面。将R、G、B三个通道的图像放在三维直角坐标系中，那么图像中的每个像素点都有自己对应的坐标，每个像素点的位置以x、y、z的坐标形式来表示，其中R通道的z1为0，G通道的z2为1，B通道的z3为2.像素点质量如公式（3）所示。

引力作用具有大小，同时也具有方向。根据图3中R、G、B三个通道的位置关系，R通道中的像素点受到的引力FG->R和FB->R方向都是向上的，G通道中的像素点受到的引力FB->G方向向上，FR->G方向向下，B通道中的像素点受到的引力FR->B和FG->B方向都是向下的。定义引力方向向上为正方向，考虑到像素间引力作用的方向都不尽相同。因此，将像素点间的引力都转化为竖直方向（即z方向）进行代数计算，水平方向上的引力作用不考虑。引力大小关系和像素点受到的合力如公式（5）和（6）所示。

公式（7）中[G]为改进万有引力的引力系数，其大小为R、G、B三通道所有像素点质量的累加和的倒数，M和m分别为两个存在引力作用关系的像素点质量，α为引力方向与水平面（即xoy平面）的夹角，d为竖直方向（即沿z方向）两点的距离。根据定义3中，考虑所有像素点间的引力作用方向都不相同，进行矢量叠加比较困难，因此都转化为竖直方向上的引力作用按照公式（5）和公式（6）进行代数和计算，只考虑外力作用，内力忽略不计。

定义5：引力矩阵

当r≤R时（R为极限距离），在这个范围内的所有像素点都存在对目标点的引力作用，按照定义1～4和公式（7）、（10）计算目标点受到的竖直方向上引力作用的代数和Fi，j，l。

Fi，j，l为目标点M受到的竖直方向上的引力代数和，MR（xi，yj，z1），i=1，2，...，N;j=1，2，...，N;l=1，2，3，N为N*N图像的水平、竖直方向上的像素个数。F、G、H为在极限距离R范围内存在着若干个点对目标点M的引力作用，其最大x坐标、y坐标、z坐标分别为F、G、H。

定义6：极限距离R的选取

根据公式（4）即可计算出两个像素点之间的距离。当距离过小，两者之间的引力作用会很大，距离过大，引力作用又会很弱。依照这一特点，规定当r足够大，即r≥R时（R为极限距离），像素间的引力作用可以忽略不计。本节选取r=71～100这个范围进行了30组改进万有引力算法的图像加密实验，选取30组实验中lena的R通道图像加密效果最佳（信息熵最大）的一组实验的距离作为极限距离，选定的极限距离为87。测试数据如表1所示。

3 图像加密步骤

步骤1：输入待加密的N*N*3初始图像Im，如图1（a）所示，将图像Im进行R、G、B三通道分层，得到IR、IG、IB三通道像素值图像，如图4所示。

步骤2：将三个通道图像IR、IG、IB按照图1（c）所示各自进行一次小波变换，得到低频、水平、垂直、對角四个子图。

步骤3：选取三个通道大小为N1*N1的低频子图LL1R、LL1G、LL1B，按照公式（2）进行158次Arnold置乱，其中选取参数a和b分别为3和5，得到LL1R、LL1G、LL1B的Arnold置乱图IR1、IG1、IB1。

步骤4：将步骤3得到的三个通道像素置乱图IR1、IG1、IB1进行一次小波逆变换得到N*N的置乱重构图IR2、IG2、IB2。

步骤5：根据上述定义1～6，计算IR2、IG2、IB2各自的引力矩阵Q1、Q2、Q3，在根据公式（11）对引力矩阵Q1、Q2、Q3进行变换，得到变换后的引力矩阵Q1、Q2、Q3。

步骤6：根据公式（12），将变换后的引力矩阵Q1、Q2、Q3与置乱重构图IR2、IG2、IB2进行异或扩散加密，得到一次异或扩散加密图IR3、IG3、IB3，如图5所示。

步骤7：根据公式（1）和（13）提取并处理混沌时间序列的N*N序列矩阵Pi，j。

步骤8：将步骤7中的序列矩阵Pi，j按公式（14）进行处理后再按照公式（15）与引力矩阵异或扩散加密图IR3、IG3、IB3再次进行异或扩散，得到加密图IR4、IG4、IB4，如图6所示。

4 安全性分析

4.1 灰度级直方图分析

图像的灰度级直方图是反映一幅图片各个灰度级像素点的个数，能有效地分析出图像是否抗统计攻击。若图像像素值比较集中，则容易通过统计的方法进行破解，反之，攻击者难以利用像素灰度级的统计特性进行破解。图7为lena图像R、G、B三个通道明文图像和密文图像灰度级直方图。图7（a）、（b）、（c）中灰度级比较集中，（d）、（e）、（f）中灰度级比较分散且均匀。由此可见，基于万有引力算法的混沌加密具有较强的抵御统计分析的能力。

4.2 图像相邻像素相关性分析

相关性指的是一幅图片相邻像素之间的关系程度。一幅图片若要表现出其意义，那么他的相邻像素通常会比较接近。有效的加密方式会使得加密后的图像的相邻像素之间关系不会那么密切。相关性分析能有效判别加密算法的优劣，本实验抽取lena的明文图像和密文图像的水平、垂直和对角三个方向各10000对像素进行测试比较。图像相邻像素相关性的计算方式如公式（16）～（19）所示。

结合表2和表3的数据可以看出lena的R、G、B三个通道的密文图像的相关性系数明显小于明文图像的相关性系数。因此，本文使用的算法更具有优良的保密性，并且具有现实可行性。表4为文献[21-23]的lena灰度密文图像的相关性系数表，通过与本文算法对比，本文算法具有一定的优越性。lena图像的R、G、B三个通道的明文图像和密文图像的相关系数图如图8、9、10所示。

4.3 密钥灵敏度分析

密钥是破解整个加密图像最关键的部分，密钥的灵敏度关系着加密图像的安全性。为了测试密钥是否灵敏，以下用几组差异较小的密钥对密文图像进行破解。用分数阶超混沌系统的其中一个初始值x0作为密钥进行试验，密钥值为0，实验取值x0=0.01，x0=0.001，x0=0.0001得到的R通道解密图如图11所示。只要密钥存在细微差别，密文图像就不能够被正常破解，被破解的图像也不能正常反映明文图像中的任何内容。因此，可以得到该算法对初值具有敏感性，能够有效抵御暴力攻击。

4.4 信息熵分析

信息熵是衡量系统的不确定程度，表现为直接获取信息的可能性和随机性。信息熵的大小与图像混乱程度有关，混乱程度越大，信息熵越大。本文使用的是单通道256*256的图像，图像最大的信息熵值为8。信息熵的计算公式如公式（20）所示。

通过计算lena图像R、G、B三个通道的明文图像的信息熵分别为7.2875、7.5439、7.0390，密文图像的信息熵分别为7.9891、7.9893、7.9890。密文图像的信息熵明显大于明文图像的信息熵，且更接近于8。说明该算法具有一定的有效性。

5 小结

本章提出基于万有引力算法的混沌图像加密方案，该算法利用五维分数阶超混沌动力学方程生成的时间序列与经过Arnold算法置亂以及万有引力算法扩散后的图像再次进行异或扩散，形成加密图像，由于分数阶混沌系统具有初值敏感性、记忆性等优良特性，以及万有引力算法的像素联合性，使得加密后的图像具有良好的抵御攻击优点。

参考文献：

[1] Bourbakis N， Alexopoulos C. Picture data encryption using SCAN pattern[J]. Pattern Recogn， 1992（25） ：567–581.

[2] Refregier B Javidi. Optical image encryption based on input plane and fourier plane random encoding[J]. Opt. Lett. 1995（20） ：767–769.

[3] Chang H K L， Liu J L.A linear quad tree compression scheme for image encryption[J]. Signal Process. 1997，10 （4） ：279–290.

[4] Chang C C， Hwang M S， Chen T S.A new encryption algorithm for image cryptosystems[J]. J. Syst. Software， 2001（58） ：83–91.

[5] Li S， Zheng X. Cryptanalysis of a chaotic image encryption method[C]. Proceedings of the IEEE International. symposium on circuits and systems， Scottsdale， AZ， USA， 2002.

[6] Li S， Zheng X， Mou X， et，al. Chaotic encryption scheme for real time digital video[C]. Proceedings of the SPIE on electronic imaging， San Jose， CA， USA， 2002.

[7] Chen G， Mao Y， Chui C.K.A symmetric image encryption based on 3D chaotic maps[J]. Chaos Solitons Fractals， 2004（21） ：749–761.

[8] Yen J C， Guo J I.A new image encryption algorithm and its VLSI architecture[C]. Proceedings of the IEEE workshop signal processing systems， 1999：430–437.

[9] Yen J C， Guo J I.An efficient hierarchical chaotic image encryption algorithm and its VLSI realization[J].IEE Proc. Vis. Image Process， 2000（147） ：167–175.

[10] Yen J C， Guo JI.A new chaotic key based design for image encryption and decryption[J]. Proceedings of the IEEE International Symposium Circuits and Systems， 2000（4）：49–52.

[11] Scharinger J.Fast encryption of image data using chaotic Kolmogrov flow[J]. J. Electronic Eng， 1998，7（2）：318–325.

[12] Fridrich J. Symmetric ciphers based on two-dimensional chaotic maps[J]. Int J Bifurcat Chaos，1998;8（6）：1259–84.

[13] Zhang Q，Guo L，Wei XP.Image encryption using DNA addition combining with chaotic maps[C].Mathematical and Computer Modelling， 2010，52（12）：2028-2035.

[14] Xue XL，Zhang Q，Wei XP，Guo L.A Digital Image Encryption Algorithm based on DNA Sequence and multi-chaotic maps[J]. Neural Network world，2010，20（3）：285-296.

[15] Zhang Q，Wang QA，Wei，XP.A Novel Image Encryption Scheme Based on DNA Coding and Multi-Chaotic Maps[J].Advanced Science Letters，2010，3（4）：447-451.

[16] Xue XL，Zhang Q，Wei XP.An Image Fusion Encryption Algorithm Based on DNA Sequence and Multi-Chaotic Maps[J].Journal of Computational and theoretical Nanoscience，2010，7（2）：397-403.

[17] Chapaneri R， Sarode T，Chapaneri S.Digital Image Encryption using  Improved Chaotic Map Lattice[C].2013 Annual  IEEE India Conference （INDICON），2013.

[18] Sun FY，Lu ZW.Image encryption using spatial chaotic map[C].International conference on image processing and pattern recognition in industrial engineering，2010.

[19] Sun FY，Liu ST.Image encryption using high-dimension chaotic system[J].Chinese Physics，2007，16（12）：3616-3623.

[20] 謝国波，吴震禹.基于小波变换和重力模型的混沌图像加密算法[J].计算机工程与应用，2019，55（13）：100-105.

[21] Orsdemir A，Altun HO，Sharma G.On the security and robustness of encryption via compressed sensing[C].Military Communications Conference，2008.Milcom.IEEE，2009：1-7.

[22] Zhou N，Pan S，Cheng S.Image compression-encryption scheme based on hyper-chaotic system and 2D compressive sensing[J].Optics & Laser Technology，2016，82：121-133.

[23] Xu L，Li Z，Li J.A novel bit-level image encryption algorithm based on chaotic maps[J].Optics & Lasers in Engineering，2012，78（21）：17-25.

【通联编辑：代影】