基于收益率分解模型的行业板块指数长记忆性研究

邱　瑾，陈　升

(浙江财经大学 数据科学学院，浙江 杭州 310018)



基于收益率分解模型的行业板块指数长记忆性研究

邱瑾，陈升

(浙江财经大学 数据科学学院，浙江 杭州 310018)

采用资产定价模型(Capital Asset Pricing Model，CAPM)将国内A股市场11个行业板块指数的收益率分解为市场超额收益率和行业本身超额收益率，使用重标极差法(Rescaled Range Analysis，R/S)和局部Whittle(Local Whittle，LW)方法，分别检验行业本身超额收益率和市场超额收益率及其波动率的长记忆性。实证结果显示，行业本身超额收益率的长记忆性要弱于市场超额收益率的长记忆性，同时行业本身超额收益率波动性的长记忆性更加受到行业本身的影响。

板块指数；行业波动率；长记忆性；CAPM模型

长记忆性指时间相隔较远的观测值之间仍存在着相互依赖性，这意味着历史事件在较长时间内仍存在对未来的影响。对于长期记忆性，最早是由水文学家Hurst在研究尼罗河水量变化的时间序列中发现的，并提出分析长记忆性的方法——重标极差分析方法(rescaled range analysis，R/S)，Hurst指数对长记忆性进行度量。近几十年，对金融时间序列的长记忆性的考察成为诸多学者研究的热点，资本市场的长记忆性认识，对于市场结构、判断市场的走势以及市场风险的测度分析了解都具有重大的意义。

国内外学者在20世纪90年代以来对金融时间序列的长记忆性进行了大量的实证研究。R/S分析方法是检验序列记忆性的经典方法。Howe[1]在对几个新兴证券市场，其中包括日本、澳大利亚等国及香港地区进行研究时，发现用经典R/S分析发现其具有长期记忆性的证据。但是R/S分析方法存在缺陷，它无法有效地区分序列的短期相关性和长期相关性。比如Lo[2]的研究发现，使用R/S分析方法将会得出有偏的Hurst指数，因此他提出了修正的R/S方法。Cajueiro[3]运用修正的R/S方法研究了美国、日本以及l1个新兴股市收益的长记忆性，证明了发达国家股票市场并不具有长记忆性。邓丰等[4]利用R/S方法，对沪铜期货价格指数在不同时间标度下收益率序列的长记忆特征进行分析，结果表明，沪铜期货价格具有长记忆性。金成晓等[5]运用ADF-KPSS联合检验法、自相关系数法、R/S检验法检验了沪深300股指期货指数的收益率及波动率序列的长记忆性，发现股指期货的收益率序列不存在长记忆性，而其波动率序列存在明显的长记忆性。随着研究的发展，半参数方法也逐渐兴起，Geweke等[6]提出关于分数维数d的估计方法，该估计量建立在谱密度函数的基础之上。Mills[7]利用修正的R/S分析和GPH检验研究了英国股市月度收益，发现英国股市存在显著的长期记忆。Robinson[8]提出了基于极大似然估计的局部Whittle(LocalWhittle，LW)方法。田华[9]采用LW估计方法研究了我国证券市场的长记忆性，并和对数周期图回归(GPH)方法进行了比较，表明LW方法不受时间频率的影响，能有效消除时间序列中短期记忆和周期性对估计结果的影响，明显优于GPH方法，其实证结果表明，中国证券市场存在明显的长记忆性，并且认为长记忆行为在重大突发事件发生期间更加明显。

上述这些实证研究大多基于综合指数或者个股序列进行长记忆性的检验，对行业板块指数收益序列的研究相对较少。本文采用CAPM模型将国内A股市场11个行业板块指数的收益率分解为市场超额收益率和行业本身超额收益率，使用R/S方法和LW方法分别检验行业本身超额收益率和市场超额收益率及其波动率的长记忆性。

1　研究方法

1.1重标极差法(R/S)估计

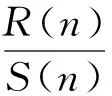
(1)

(2)

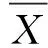
1.2局部Whittle(LW)估计

局部Whittle估计方法无需预先假定模型的具体形式，但该方法要求时间序列{Xt}的谱密度f(λ)有明确的参数形式，即

f(λ)→G(H)|λ|1-2H,λ→0

(3)

其中G(H)为常数。此外还包括其他参数窗宽m， m一般选取小于N/2的整数(N为时间序列长度)，并满足

(4)

当谱密度函数f(λ)满足(3)时，高斯似然函数的Whittle估计为

(5)

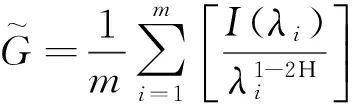
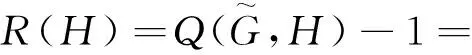
(6)

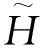
(7)

且当N→∞时，Robinson证明了

(8)

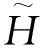
2　实证研究

2.1样本选择与数据说明

根据上述研究方法，选取上证综合指数，以及银行、医药、汽车类、家用电器、食品饮料、农林牧渔、化工、有色、钢铁、煤炭、房地产等11个行业板块指数的日收盘数据。这些行业板块指数中包括了银行、汽车、钢铁、煤炭、房地产、有色等周期性行业，也包括了食品饮料、医药等非周期性行业。这些行业也分别囊括了第一产业、第二产业、第三产业，故所选取的这11个行业具有较好的代表性。以上板块数据全部来自Wind金融终端，样本时间区间为2005年7月1日至2015年7月1日。收益率采用日对数收益率，并用日对数收益率的平方来代替各个指数的波动率。

2.2每个行业收益结构分解

在本文的研究中，将各个行业的超额收益率(收益率减去无风险收益率)分解为市场超额收益率和行业水平超额收益率，并将行业收益率中超过无风险利率的部分定义为行业超额收益率。使用CAPM模型分解得到正交的收益率：

Rit=βi×RMt+Xit

(9)

其中，Rit为行业i的超额收益率；RMt为市场超额收益率，βi为行业i超额收益率相对市场超额收益率的贝塔系数；Xit为行业i的超额收益率中无法用市场超额收益率分解的那部分，也即行业i特有的超额收益率。行业超额收益率与市场超额收益率运用OLS方法进行时间序列回归，可以得到βi和Xit的估计值。

为得到(9)式中的行业超额收益率Rit和市场超额收益率RMt，采用的无风险收益率是人民币一年期定期存款利率。自2005年7月1日至2015年7月1日，人民币一年期存款基准利率一共调整了39次。市场收益率用上证综合指数的日收益率代替。

2.3实证结果

表1是经收益率分解前行业超额收益率和波动率的Hurst指数。

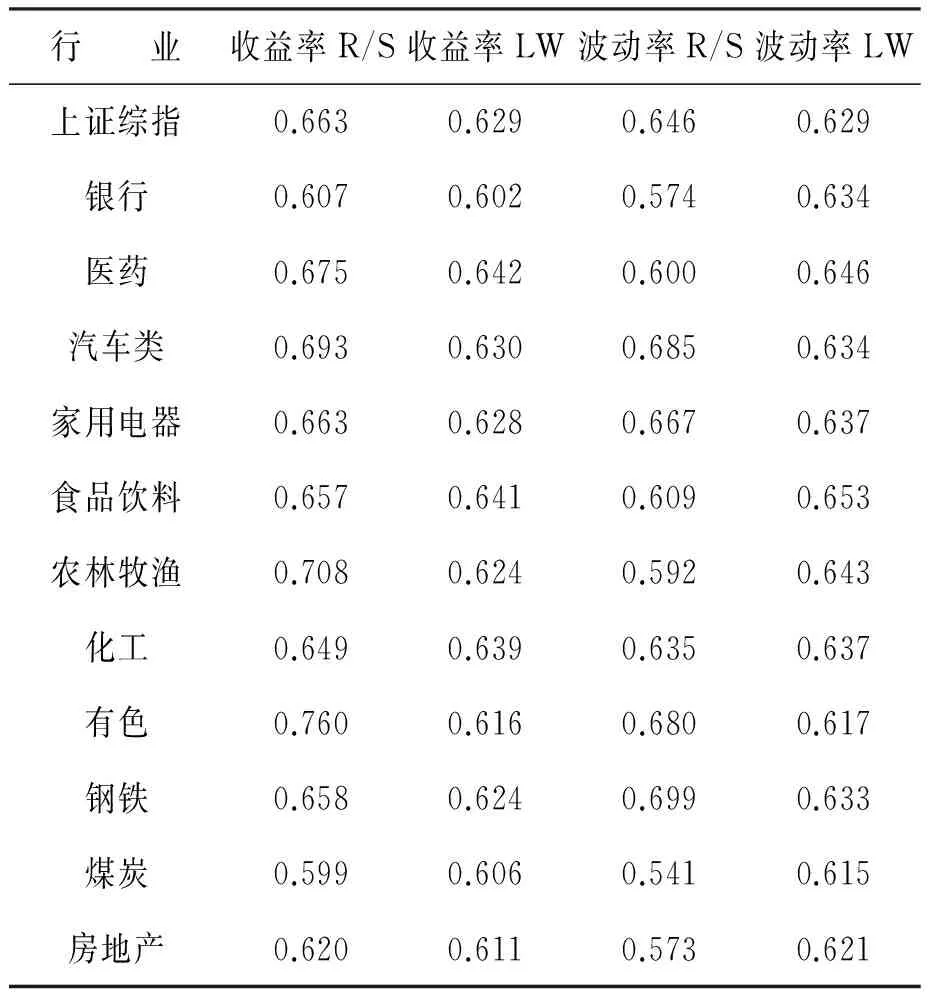
表1　收益率分解前的行业超额收益率和波动率的Hurst指数

在表1的结果中，从收益率来看，用R/S和LW方法下计算得到的Hurst指数并没有较大的差异，说明计算结果具有较好的稳健性。上证综合指数以及11个行业板块指数收益率都存在长记忆性，其中医药、有色、农林牧渔等行业指数收益率的长记忆性相对较强，银行、煤炭、房地产等行业指数的长记忆性相对较弱。从超额收益率的波动率来看，上证综合指数以及11个行业板块指数的波动率序列表现出长记忆性，其中汽车、化工、钢铁行业等板块指数的波动性的长记忆性相对较高，银行、房地产等板块指数波动性的长记忆相对较弱。比较表1中行业超额收益率和波动率的长记忆性可以发现，结果未明显地表现出已有文献中所得到的波动性的长记忆性大于收益率本身的长记忆性[10-11]，这可能显示出行业板块收益序列和综合指数及个股收益序列存在着一定的差异，有进一步研究的必要。

通过CAPM模型将行业超额收益率分解得到行业本身特有超额收益序列来计算Hurst指数的结果如表2所示，从行业本身特有超额收益序列来看，上述11个行业板块指数收益率都存在长记忆性，但是银行行业板块特有超额收益率在使用R/S方法的结果显示并不存在长记忆性，其中医药、化工等行业板块特有超额收益率的长记忆性相对较强。同时行业特有收益的波动率都存在长记忆性。比较行业本身特有超额收益率和波动率的长记忆性可以发现，波动性序列的长记忆性要明显地大于收益率序列的长记忆性，这一结果与文献[10-11]的结果是相近的。

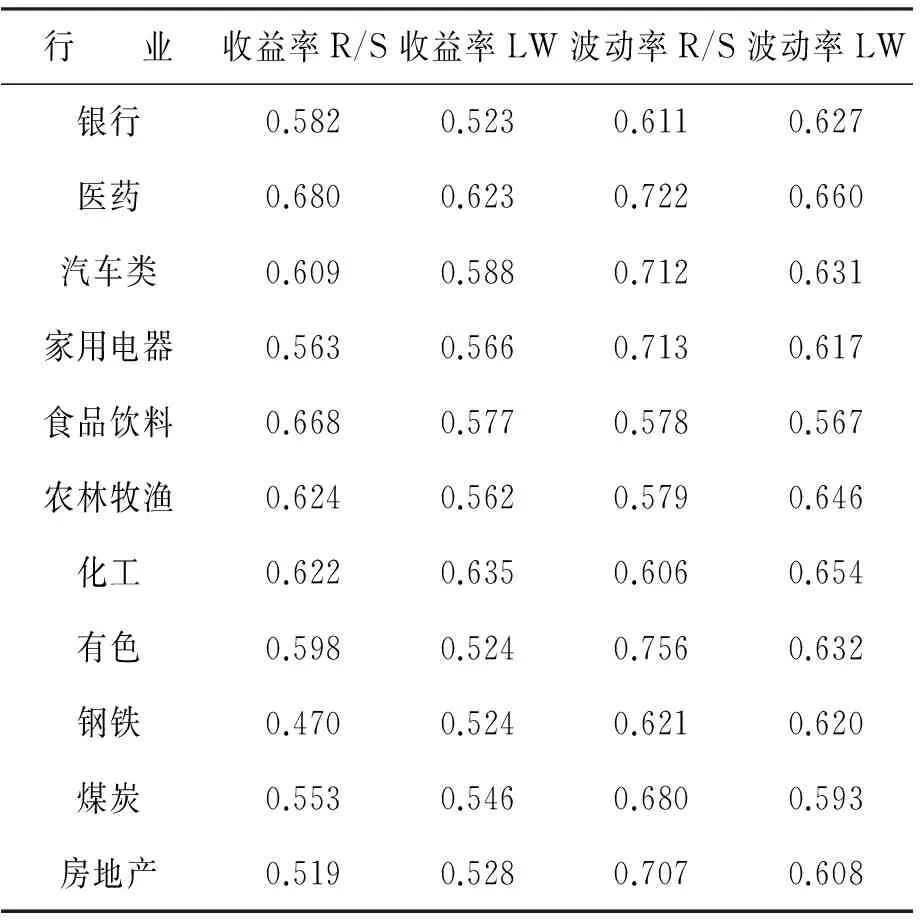
表2　收益率分解后的行业特有超额收益率和波动率的Hurst指数

比较表1和表2的结果可以发现，行业本身特有的超额收益率序列的长记忆性要小于行业超额收益率序列的长记忆性，也就是说行业超额收益率的长记忆性主要来自于市场超额收益率的长记忆性，较小部分来自于行业本身特有的超额收益率的长记忆性。这即要求分析不同行业收益率长记忆时需要首先考察市场超额收益率的长记忆性。同时，比较行业特有的超额收益率的波动率和行业超额收益率的波动率的长记忆性，并非一致地大于或者小于，这体现了行业本身波动性的长记忆性更加受到行业本身的影响。然而金融时间序列波动性所表现出的长记忆性反映在风险上，即当前的风险对未来风险的影响，那么对于市场中的长期投资者和监管层就不得不考虑这种持续性的存在与否以及程度强弱。上述实证结果对于资产组合配置、投资风险管理具有重要意义。

3　结　　论

行业板块是根据上市公司所属的行业属性来进行划分的。某一行业诸多公司的发展状况及其景气周期具有较高的相似性，且具有共同的行业性质。本文采用了收益率分解模型，将收益率分解为市场超额收益率和行业本身超额收益率，采用重标极差法(R/S)、局部Whittle(LW)方法对11个行业板块指数在对收益率分解前后的长记忆性进行了检验。结果发现行业板块指数超额收益率存在长记忆性。比较收益率分解前后的长记忆性检验结果，发现行业本身特有的超额收益率的长记忆性要小于行业超额收益率。同时，比较行业特有的超额收益率的波动率和行业超额收益率的波动率的长记忆性，并非一致地大于或者小于，这体现了行业本身超额收益波动性的长记忆性更加受到行业本身的影响。

上述结果对于股票市场中的参与者有着深远的意义。对于投资者而言，由于长记忆性的存在，那么当前市场的状况将会对未来的市场走势产生持续的影响，因此在投资的过程中，确定投资决策就必须考虑这种长期记忆性的影响，从而更好地为获取收益和规避风险服务。同时由于行业本身收益率的长记忆性要小于市场本身收益的长记忆性，那么在选择目标股票进行投资时，要尤其关注市场本身所处状态。投资者考虑风险时要特别关注影响该行业的重大事件对该行业未来的影响。由于中国股市存在长记忆性，即当前的事件将影响未来市场的运行，那么对于股市的监管部门而言，政策的制定和修改尤其需要慎重，重大突发事件的发生，或带来了更大的波动。特别是在突发事件发生时而采取应急措施，不能光顾着这一政策对当前的作用，而忽视其对未来的影响。

[1] Howe J S, Martin D W, Wood B G. Much ado about nothing: long-term memory in Pacific Rim equity markets[J]. International Review of Financial Analysis, 1999, 8(2): 139-151.

[2] Lo A W. Long-term memory in stock market prices[R]. National Bureau of Economic Research, 1989.

[3] Cajueiro D O, Tabak B M. The rescaled variance statistic and the determination of the Hurst exponent[J]. Mathematics and Computers in Simulation, 2005, 70(3): 172-179.

[4] 郑丰,崔积钰,马志伟. 沪铜期货市场长记忆特征的R/S分析[J]. 辽宁大学学报(自然科学版),2013,40(1): 14-20.

[5] 金成晓,王继莹.沪深300股指期货收益率及波动率的长记忆性研究[J].北京理工大学学报(社会科学版), 2014,16(5):89-93,102.

[6] Geweke J, Porter‐Hudak S. The estimation and application of long memory time series models[J]. Journal of time series analysis, 1983, 4(4): 221-238.

[7] Mills T C. Is there long-term memory in UK stock returns?[J]. Applied Financial Economics, 1993, 3(4): 303-306.

[8] Robinson P M. Gaussian semiparametric estimation of long range dependence[J]. The Annals of statistics, 1995: 1630-1661.

[9] 田华.基于LW估计的中国证券市场长记忆性实证研究[J].北京理工大学学报(社会科学版),2007,9(3):110-113.

[10] 施红俊,马玉林,陈伟忠.中国股市长记忆性实证研究[J].同济大学学报(自然科学版),2004,32(3):416-420.

[11] 杨桂元,赵宏宝.中国股市收益率和波动率的长记忆性检验[J].统计与信息论坛,2009,24(6):39-43.

Empirical Study of Long Memory in China Sectoral Indices Based on Stock Returns Decomposition Model

QIU Jin，CHEN Sheng

(School of Data Sciences, Zhejiang University of Finance & Economics, Hangzhou, Zhejiang 310018, China)

This paper applies the CAPM model to decompose the return rates of 11 industry sectors in stock market of China into the excess returns from the market and those from the industry itself, and then uses R/S and LW analysis methods to investigate their long memories. The results show that the long memory of the excess returns from the industry itself is weaker than the long memory of the excess returns from the market, and the long memory of the volatilities of the excess returns from the industry itself is more dependent on each industry.

sectoral indices; industrial volatility; long memory; CAPM model

2016-03-12

国家社会科学基金项目(14BTJ031)，浙江省自然科学基金项目(Y14A010064)，教育部人文社会科学重点研究基地重大项目(13JJD910002)和浙江省统计研究重大课题“离散因变量空间计量模型的统计推断”。

邱瑾，女，浙江长兴人，博士，浙江财经大学数据科学学院教授，研究方向为面板数据分析、空间计量经济学、概率极限理论等。E-mail：qiujin_71@hotmail.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.010.html

C812

A

1007-4260(2016)03-0031-04

10.13757/j.cnki.cn34-1150/n.2016.03.010