双加权Schatten-p范数最小化彩色图像去噪

姜 伟， 杨天旭， 张长胜

(1.辽宁师范大学 数学学院,辽宁 大连 116029; 2.温州大学 计算机与人工智能学院,浙江 温州 325035)

随着现代数字技术的高速发展，数字图像获取更加容易并得到了广泛的应用，但由于光照、传播等各类因素的影响，图像通常会含有噪声.例如，在人脸识别系统中，往往假设是在理想的光照情况下，然而，在诸如门禁安全系统、嫌疑人识别和安全监控系统等实际应用中，理想假设条件是不满足的.Moses等[1]在实验中表明，不同光照条件下拍摄的同一个人的人脸图像，在灰度上表现出来的差异远比在相同光照条件下拍摄的不同人的人脸图像在灰度上表现出来的差异要来得大，这就造成了实际情况与数学模型之间的偏差.数字图像的本质是信号，因此，在信息获取过程中信号的噪声也会同样发生在图像获取中，这种噪声可能来自采样信道的高斯噪声[2-6].对大规模的带有噪声的数字图像进行有效的处理，并充分挖掘数字图像的本质，已经成为学术界致力探索的一个新方向.

数字图像主要包括灰度图像与彩色图像两大类，灰度图像去噪算法主要有加权核范数方法(Weight nuclear norm minimization，WNNM)[7]、加权Schatten-p范数方法(Weight Schatten-pnorm minimization，WSNM)[8]等.对于彩色图像去噪算法，彩色三维块匹配算法(Color block-matching and 3D filtering，CBM3D)[9]是一种代表性的算法，它首先将RGB图像转换到一个低维空间，然后在每个通道分别用基准三维块匹配算法 (Block-matching and 3D filtering，BM3D)[2]进行去噪.Liu等[10]提出了“噪声级函数”，用来评估并去除每个通道内的噪声.然而，单独处理每个通道要比将彩色通道联合起来进行处理效果差很多，原因是忽略了各个通道的自相似性.文献[11]提出了基于卷积神经网络(Convolutional neural network，CNN)的快速去噪算法，将输入的图像重塑为4个子图像，并与噪声等级一起输入CNN，但没有考虑到各个噪声通道的噪声等级不同，导致效果不尽如人意.随后，Xu等[12]考虑了图像的自相似性以及不同通道内的噪声统计量提出了多通道加权核范数最小化(Multi-channel weight nuclear norm minimization，MC-WNNM)算法，该算法利用图像非局部自相似块的低秩先验，并引入了加权矩阵，根据不同的噪声等级对各个通道进行均衡.然而，在某些情况下，核范数并不是低秩的最优凸逼近.文献[13]提出了三边加权稀疏编码方法，但在求解时会需要高的计算代价.

为了解决彩色数字图像算法存在的问题，提出了一个新的真彩色图像去噪模型，即基于双加权Schatten-p范数RGB彩色图像去噪模型.由于Schatten-p范数[14]相比较于核范数在处理低秩问题来说更具灵活，当p=1时，Schatten-p范数即退化为核范数.

1 模型建立与求解

1.1 灰度图像的加权Schatten-p范数模型

灰度图像的加权Schatten-p范数模型被表示为

(1)

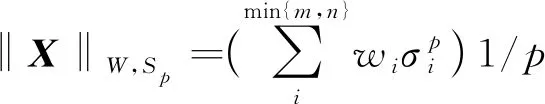
(2)

目标函数(1)有封闭解[14]：

(3)

其中，Y=UΣVT是Y的奇异值分解，且Sw(·)是带有权重w的软阈值算子.

加权Schatten-p范数在灰度图像上展现出了极强的去噪性能，然而，如果直接将加权Schatten-p范数应用于彩色图像上，即分别在R，G，B 3个信号通道上分别去噪，就会忽略每个通道中噪声等级不等情况，导致最后的结果不理想.所以提出一个双加权Schatten-p范数最小化去噪模型用于彩色图像去噪.

1.2 彩色图像的加权Schatten-p范数模型

标准R，G，B空间的噪声可以被近似地模拟为加性高斯白噪声，但是在一般情况下，不同的通道内的噪声的方差是不同的.考虑在不同通道内有不同的噪声强度，引入一个加权矩阵去平衡R，G，B通道里的噪声.由此提出如下双加权Schatten-p范数最小化去噪模型：

(4)

其中，Ω是权矩阵.

1.3 设置权重矩阵

(5)

对数似然项ln P(Y|X)是噪声统计量，假设R，G，B通道内的噪声是独立且同分布[15]，满足高斯分布和标准差{σr,σg,σb}，有

(6)

对于加权Schatten-p范数，采用概率分布表达为

(7)

由式(5)～式(7)得到：

(8)

其中，

(9)

其中，I是单位矩阵.权重矩阵Ω是对角矩阵，由每个通道内的噪声标准差定义，每个通道内的噪声强度越强，在估计X时给予一个小的权重，使得在噪声强度越小的通道可以给出X的较大的贡献.如果各个通道内噪声强度相同的话，只需要简单地对各个通道分别去噪再聚合即可，此时权重矩阵退化为单位矩阵.

1.4 模型求解

在加权Schatten-p范数模型中，当权重分配给奇异值时是非升序的，加权Schatten-p近端算子有一个最优且是闭式解.由于权重矩阵Ω被分配给了X的行，这使得目标函数是不可分，使所提出的去噪模型比加权Schatten-p范数模型难解.

用变量分裂方法[16]去解决上述问题，通过辅助变量Z，可以转化为含可分的2个变量的等式约束最优化问题，即

(10)

目标函数(10)在交替乘子方向法(Alternating direction method of multipliers，ADMM)框架下进行求解，其增广拉格朗日函数为

.

(11)

其中，A是增广拉格朗日乘子并且ρ>0，目标函数(11)是一个具有3个未知变量的优化问题，采用固定其中2个，求解另一个的方法进行求解，具体如下：

(1)固定Z和A，更新X

(12)

这是一个最小二乘问题，有一个封闭解，

(13)

(2)固定X和A，更新Z

.

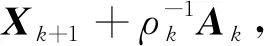
(14)

.

(15)

(3)固定X和Z，更新A

Ak+1=Ak+ρk(Xk+1-Zk+1)

.

(16)

(4)更新ρk

ρk+1=μ×ρk.

(17)

交替更新步骤直到满足收敛条件或者达到预设迭代次数停止.收敛条件为：‖Xk+1-Zk+1‖F≤Tol，‖Xk+1-Xk‖F≤Tol并且‖Zk+1-Zk‖F≤Tol，Tol是一个非常小的值.具体描述如算法1.

算法1:MCWSNM基于ADMM法迭代更新过程 输入:矩阵Y和W,μ>1,Tol>0,K1;初始化:X0=Z0=A0=0,ρ0>0,T=False,k=0;While(T=False),do a)迭代更新Xk+1:Xk+1=ΩTΩ+ρk2I-1 ΩTΩY+ρk2Zk-12Ak ; b)通过求解如下问题迭代更新Zk+1: argminZρk2‖Z-Xk+1+ρ-1kAk ‖2F+‖Z‖pw,Sp; c)迭代更新Ak+1: Ak+1=Ak+ρkXk+1-Zk+1 ; d)迭代更新ρk+1: ρk+1=μ×ρk; e)k=k+1; if(收敛条件满足或者k≥K1) f)T=True; end ifend while输出:矩阵X和Z.

算法2:基于MCWSNM的彩色图像去噪算法输入:噪声图像yc,噪声级σr,σg,σb ,K2;初始化:x(0)c=yc,y(0)c=yc;for k=1:K2 do a)设置yk c=xc; b)提取局部块yjj=1,…,N ; for eachyj do c)搜索非局部相似块Yj; d)对Yj调用算法1得到Xj; end for e)聚合Xj为xc;end for输出:去噪图像xK2 c.

2 实验结果与分析

2.1 实验参数设置

为了评价所提出的算法在处理不同的图片去噪性能，选取了图1中的4幅大小为512×512×3彩色图片用来做对比实验.在3种不同的通道上添加不同级{σr,σg,σb}={40，20，30}与{σr,σg,σb}={65，55，50}的高斯噪声，对每张图片的各个通道加入了不同的噪声.实验对比的算法包括：本文算法，MC-WNNM[11]，CBM3D[9].

图1 图像去噪的4个测试图像Fig.1 The 4 test images for image denoising

2.2 实验结果及分析

为了评估本文提出的算法的定量特性，通过比较峰值信噪比[17](PSNR)，以及结构相似度[17](SSIM)两种被广泛应用于评估去噪性能来评估算法的定量特性.图2表示在{σr,σg,σb}={40，20，30}噪声级下的实验结果对比，图3表示{σr,σg,σb}={65，55，50}噪声级下的实验结果对比.表1显示了在{σr,σg,σb}={40，20，30}噪声级下平均定量指标对比结果，表2显示了在{σr,σg,σb}={65，55，50}噪声级下平均定量指标对比结果.

图2 不同方法在4个图像上去噪声结果Fig.2 Denoising results on the 4 images by different methods

由图2中可以看出，在低等级噪声下各类去噪算法的主观去噪效果差别不大，但是在表1中可以明显看到，在峰值信噪比方面，本文算法相较于其他两种算法均有明显提高，每张图片的峰值信噪比都达到30 dB.相对于其他两种算法，平均提升最高可达到2 dB，SSIM也明显高于其他两种算法.

图3 不同方法在4个图像上去噪声结果Fig.3 Denoising results on the 4 images by different methods

在图3中，由于噪声级的增加，实验对比的效果更加明显.在主观视觉效果，MC-WNNM有很多未被完全去除的噪声斑点，在CBM3D中，去噪图像稍显模糊.本文所提出的双加权Schatten-p范数最小化在未被去除的噪声斑点的数量与图像的清晰度，都有更好的效果.

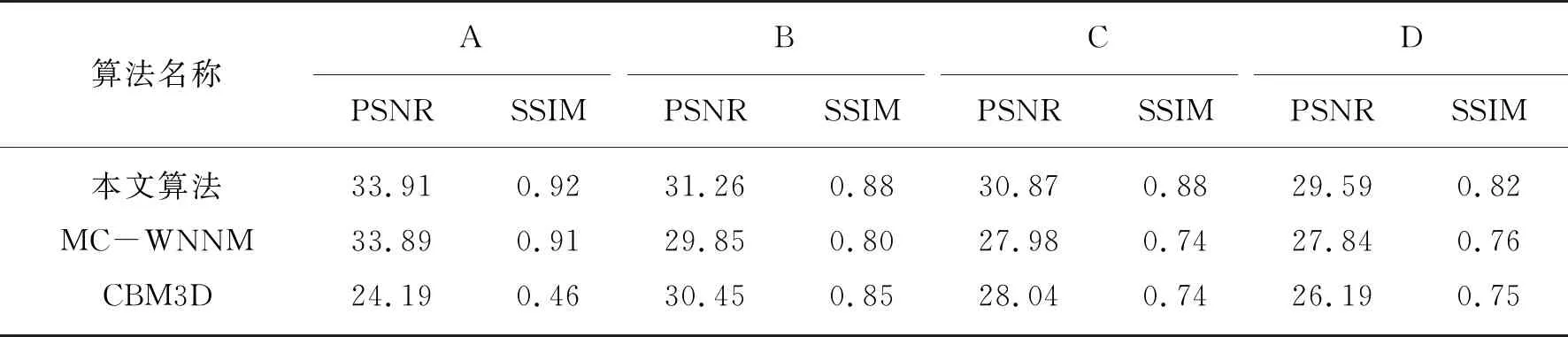
表1 不同方法去噪结果(PSNR，SSIM)实验结果对比

表2显示在{σr,σg,σb}={65，55，50}等级噪声下PSNR和SSIM值，本文所提出的算法PSNR明显高于另外两种对比算法.平均峰值信噪比达到27 dB，相较于另两种算法最高增益可达10 dB.在SSIM方面，本文所提出的算法总体上也高于MC-WNNM、CBM3D算法，并且最低提升0.01，在每张图片的不同算法平均增益可达0.1.

表2 不同方法去噪结果(PSNR，SSIM)实验结果对比

从上述实验结果可以看到，相比于目前对于彩色图像去噪效果较好的MC-WNNM、CBM3D算法，本文所提出的算法在图像恢复问题上，可以达到更高的PSNR和SSIM值和更好的视觉效果.

3 结束语

针对彩色图像去噪，提出了以Schatten-p范数作为低秩惩罚项的多通道双加权Schatten-p范数最小化算法，考虑联合处理不同通道噪声以及不同通道的噪声统计量，保证了去噪效果的优越性.在后续工作中，将对提升算法时间效率、引入新形式的对角加权矩阵以及扩展到高光谱图像分析领域进行研究.