基于PSO优化VMD和SVM的转子碰摩识别

魏永合，姜庆涛，曹 怀

(沈阳理工大学 机械工程学院，沈阳 110159)

在旋转机械中，最重要的部件是由转子和定子组成的转子系统，通过对转子系统存在的故障进行识别研究进而排除故障是整个机械系统稳定运行的重要前提。随着科学的进步发展与工业的现代化，旋转机械设备正向着高速化、大型化、精密化、集中化和大功率、大载荷的趋势发展，对其要求也越来越高，特别要求转子静子之间的间隙不断变小，这会导致碰摩故障发生的可能性越来越大。当碰摩故障发生时，产生剧烈振动，人和机械安全性降低，轻则使机械运转异常，重则造成破坏或重大事故[1]。Bohnsted J等调查发现，旋转机械损坏事故中的13%是由碰摩故障导致[2]。在国内200MW机组的事故中由动静碰摩故障引发的占到86%[3]。因而，科学指导检查和维修工作，显得尤为重要，其可以避免盲目停机检修以及碰摩故障带来各种潜在的安全问题，同时可以掌握碰摩程度以及状态识别。

信息采集与处理、模式识别与故障诊断是机械故障诊断最主要的两步。信息采集与处理：对信号进行采集以及处理，其中提取出有效故障特征是目前识别技术中难度最大的步骤。于德介等[4]利用经验模态分解算法(Empirical Mode Decomposition，EMD)将转子系统的振动信号分解，得到本征模态分量(Intrinsic Mode Function，IMF)，选择奇异值熵作为特征，然后对转子系统模式识别。Jiao W等[5]利用局部均值分解算法(Local Mean Decomposition，LMD)以转子-轴承系统不同的三种故障为例进行了分解。Dragomiretskiy K等[6]提出变分模态分解(VMD)算法，该算法不存在端点效应、模态混叠等。刘尚坤等[7]将VMD方法进行改进，并结合Hilbert谱，成功对转子故障中的油膜失稳故障进行了诊断分析。现有模式识别算法中，一般用神经网络算法对故障进行识别，但目前神经网络存在的最大缺点是需要大量的样本进行训练，而在实验中，一般提取到的数据样本是有限的。Cortes C等[8]针对神经网络的缺陷在20世纪90年代后期提出了支持向量机，支持向量机是以统计学理论作为支撑。郑近德等[9]通过支持向量机完成了几种轴承故障的有效诊断。

本文主要研究转子不同程度碰摩时的振动信号，经过详细分析，决定先采用优化VND的参数，然后采用优化SVM的参数，进而建立最理想的识别模型，提高识别准确率。

1 VMD算法基本原理

VMD是一种新的自适应信号预处理方法，分解过程实质是变分问题的迭代求解，可分为变分模型的建立和求解，是建立在Hilbert变换和外差解调等理论基础上的自适应信号分解方法[10]。VMD假定原始信号f(t)求解是通过

(1)解析各模态分量得到解析信号的单边频谱，为

(1)

式中：σ(t)为冲击函数；i为虚数单位；t为时间；uk(t)为模态函数；k为正整数。

(2)通过各模态分量的中心频段乘以一个预估中心频率e-iωkt，将中心频段调制到基频带上。

(2)

式中：ωk为模态的中心频率；e-iωkt为预估中心频率；e为自然常数。

(3)ωk的带宽的计算方法为

(3)

式中∂t为梯度的L2范数。

(4)最终得约束变分问题为

(4)

式中：{uk}为uk(t)函数取值集合；{ωk}为ωk集合；uk是当t为某一值时uk(t)函数的值；s表示传递函数。

约束变分问题转变成非约束变分问题，变换结果可表示为

(5)

式中：λ为格朗日因子；α为惩罚因子；λ(t)为格朗日因子随时间t变化函数。

各模态频域更新：

(6)

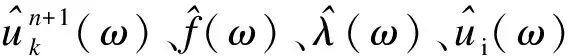
中心频率更新：

(7)

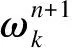
其中影响VMD分解精度的主要有两个参数：一是模态分量个数K；另一个是惩罚因子α。

2 SVM算法基本原理

SVM适用于小样本的机械故障诊断，惩罚参数C和核函数参数σ为影响SVM分类性能的主要因子[11]。支持向量机基本原理清晰、简单，就是通过其内部算法将数据从低维空间映射到高维特征空间中，因为低维空间不可分，高维空间可分，所以易于分类。实现上述方法需要利用核函数，而选择的核函数不同，分类效果不同，其原理如下。

(1)低维非线性空间到高维线性可分空间的数据映射，可表示为

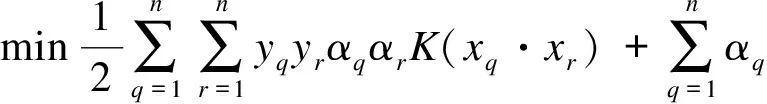
(8)

式中：yq为原始数据在q方向的映射；yr为原始数据在r方向的映射；αq为q方向的映射参数；αr为r方向的映射参数；K(xq·xr)为核函数；xq为X轴q方向坐标；xr为X轴r方向坐标。

(2)判别函数的非线性问题可表示为

f(x)=sgn(αqyqK(xq·xr)+b)

(9)

式中：f(x)为创建的判别函数；b为分类阀值。

核函数的选取直接影响分类模型的分类能力，在构建支持向量机分类模型中有多种核函数可以进行选择。根据实验特点、以往经验和分类效果理想程度，选用径向基核函数。

(10)

其中影响模型识别准确率的主要有两个参数：一是惩罚参数C，超出样本的误差范围由C的取值大小决定；另一个是核函数参数σ，决定径向基函数的宽度，所以σ的取值大小对分类结果影响明显。

3 基于PSO优化VMD和SVM参数的碰摩程度识别模型的建立

3.1 PSO原理

粒子群优化算法是1995年Kennedy J等[12]提出的优化算法。粒子群优化算法是群体性、智能化的算法，是从鸟群和鱼群的觅食过程中总结出来的。PSO具有并行的特点，需要调整的参数很少、容易实现，无需梯度信息。

其原理是各粒子通过学习不断更新自身速度和位置来搜索其个体局部极值和种群全局极值，所以该算法是一种全局寻找适应度最优位置算法，公式

(11)

(12)

式中：1≤l≤m；1≤d≤D；Vl=[vl1，vl2，…，vld]T为第l个粒子的搜寻速度，也可以表示为一个D维的向量；D为空间维度；w为惯性权重；c1、c2为学习因子；η在[0，1]间的任意数；Pl=[pl1，pl2，…，pld]T为第l个粒子个体局部极值；Xl=[xl1，xl2，…，xlD]T为一个种群由m个粒子组成，其中第l个粒子的位置可以表示为一个D维的向量；m为种群规模；h为当前迭代次数。

3.2 VMD参数优化

设定种群规模m=20；学习因子c1=2，c2=2；惯性权重w=1；Xmax=Vmax=1。

以包络熵作为适应度函数，对于零均值信号x(j)(j=1，2，…，n)的包络熵表达式为

(13)

式中：Ep是包络熵；Pj是a(j)的归一化形式；a(j)是x(j)包络信号。

(1)该算法所需要的参数根据经验设定，并人为选择优化过程中适应度函数，即包络熵值函数。

(2)粒子的位置是初始化参数[K，α]组合，并作为每个粒子初始化的移动速度。

(3)处在不同位置的各个粒子，计算相应的适应度值，选择最小包络熵为个体局部极值。

(4)对比适应度值大小和不断更新个体局部极值和种群全局极值。

(5)粒子的速度和位置不断更新利用式(11)、(12)完成。

(6)循环迭代，没有达到种群极值，返回步骤(3)，迭代完给定的值后，得到优化结果中各参数的值及与之对应的适应度值。

3.3 SVM参数优化

选择种群规模m=20；学习因子c1=2，c2=2；惯性权重w=0.6；Xmax=Vmax=1。

将分类器正确率的倍数作为适应度函数，以达到目标优化最大化。

maxF(C，σ)=150η
Cmin≤C≤Cmax
σmin≤σ≤σmax

(14)

式中：F为适应度函数；C和σ存在取值C∈(0.01，1500)和σ∈(0.01，1500)的范围。

PSO优化SVM参数过程与PSO优化VMD过程相同，区别是以[C，σ]作为初始粒子位置。SVM诊断模型流程图如图1所示。

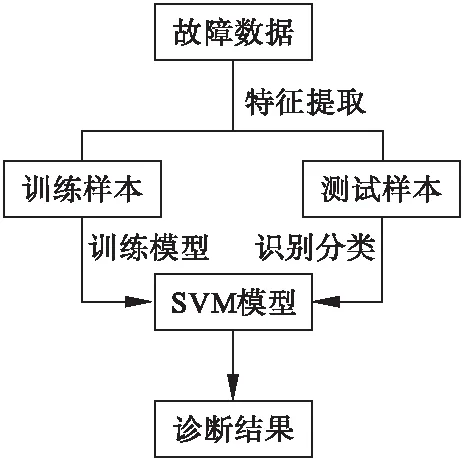
图1 SVM诊断模型流程图

首先，从故障信号的不同角度构造特征向量集；将采集到的数据集按比例分为训练样本和测试样本；SVM分类器模型对训练样本进行训练，通过训练得到最理想参数和最理想分类模型；将测试样本放到训练样本训练完成的分类模型中进行识别，最后得到训练出的SVM分类模型的识别准确率。

3.4 碰摩程度识别模型

转子碰摩故障的识别流程图如图2所示。

图2 转子碰摩故障的识别流程图

第一步：通过设计实验，模拟出不同程度的碰摩故障，并对故障信号进行采集。

第二步：为了统一量纲和方便计算，将故障信号归一化处理。

第三步：利用优化参数后的VMD算法对归一化处理后的原始信号进行分解。根据相关系数法，挑选出相关性高的模态分量进行重构信号，达到对原信号降噪的效果，并对重构信号进行故障特征的提取，构造特征向量集。

第四步：将最优参数带入到分类器模型中，对测试样本进行模式识别。

4 实验验证

通过实验，进一步说明本文提出的特征提取与模式识别方法在实际应用中的可行性和有效性。

4.1 实验设备

采用美国本特利RK-4转子实验台，转子转动通过直流电机、联轴器带动；选用两个呈90°分布在转轴上的涡流位移传感器对其x和y方向上的振动位移信号进行采集，实验仪器如图3所示。信号采集设备采用亿恒MI-7008i，其可进行实时数据分析及记录；转速调节器可在0～10000rad/min范围内进行无级调速；通过调节铜棒的位置模拟碰摩。

图3 RK-4转子实验台

4.2 实验方案

实验设计在油膜力的作用下，通过不断调整碰摩棒的位置，改变碰摩棒与圆盘之间的间隙。实验设计的参数为：转子转速1200rad/min，采样频率1500Hz，采样点数2048个。

4.3 参数优化及信号分解

使用PSO优化VMD参数，如表1所示。

表1 最优参数

将最优参数带入到VMD分解算法中，分解结果如图4所示。

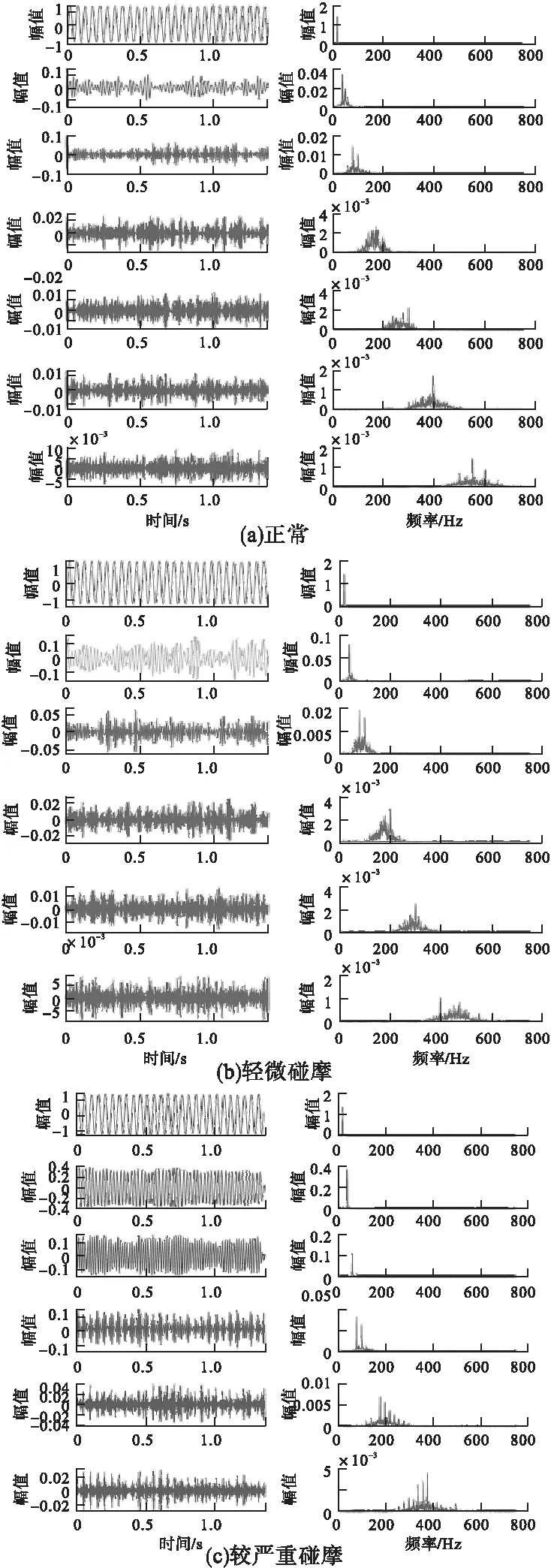
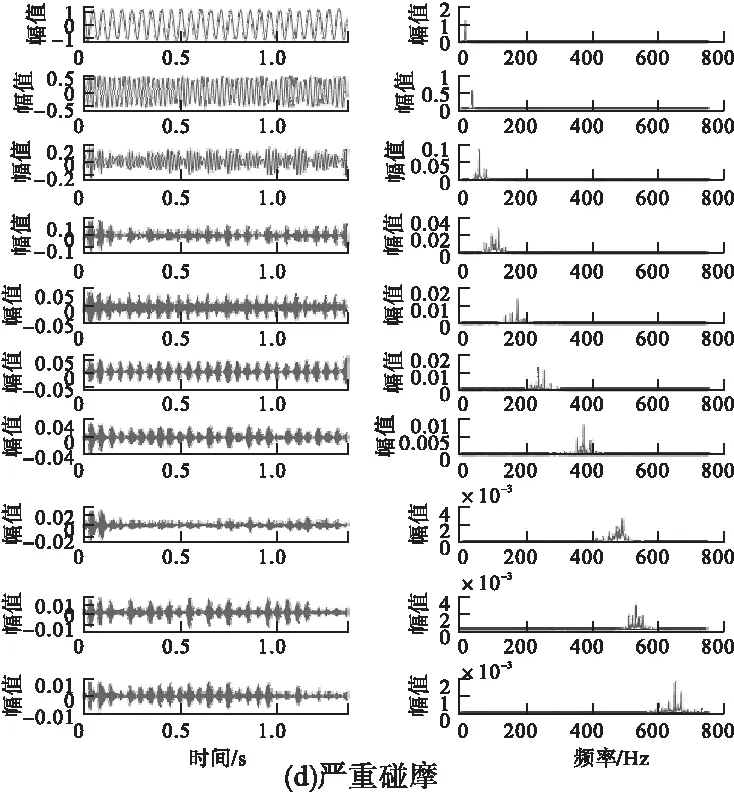
图4 VMD分解结果

4.4 选取有效模态分量

选取有效模态分量利用皮尔逊相关系数法。皮尔逊相关系数法用字母r表示。

(15)

式中：r(X，Y)为对变量X和Y间的线性相关性的衡量；Cov(X，Y)为X和Y的协方差；Var[X]为X的方差；Var[Y]为Y的方差。图5为油膜下调整碰摩棒各IMF相关系数图。

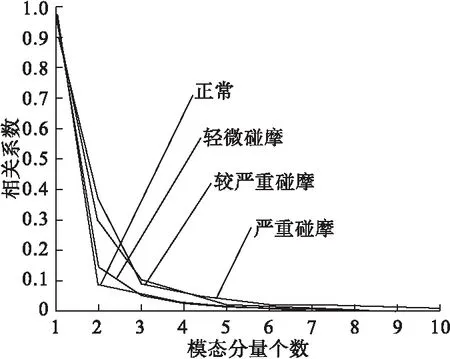
图5 油膜下调整碰摩棒各IMF相关系数图

由图5可知，不同程度信号经VMD分解后其各模态分量的相关系数在第三分量处差距最为接近，综合考虑，本文选择前三个模态分量作为有效模态分量。

4.5 提取特征构造特征向量集

通常选取时域、频域、时频域特征构造特征向量集。计算三个模态分量的能量值作为时频域特征；通过用三个有效模态分量重构信号，计算其均值、绝对均值、方差、标准差、均方根、峭度、波形因子、峰峰值、峰值因子、裕度、信息熵作为时域特征；频率均值、频率标准差、频率均方根值为频域特征。利用上述特征构造特征向量集。

4.6 参数优化及模式识别

图6为PSO优化SVM参数结果。

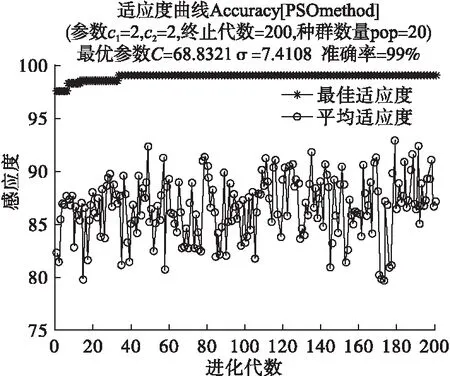
图6 PSO优化SVM参数结果

由图6可知，经PSO优化后SVM分类模型中的参数惩罚因子C和RBF核函数的参数σ分别为68.8321和7.4108。

本次实验每种故障状态采集数据175组，按4∶3比例将每组故障状态采集数据划分成训练样本和测试样本，并标记不同的标签，用来验证准确度。上述最优参数利用测试样本得出。

通过最优参数构建SVM模型，并将测试样本带到SVM模型中进行识别分类。识别结果如图7所示。

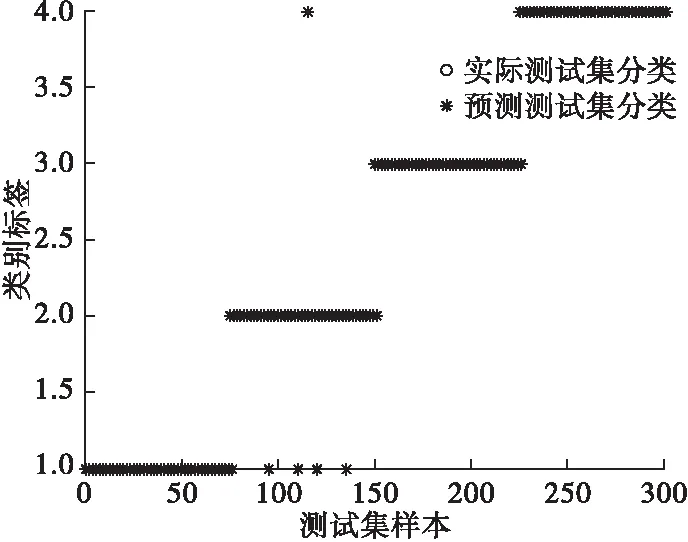
图7 测试集的实际分类和预测分类图

表2 识别结果

由图7和表2可知，支持向量机模型进行粒子群优化算法优化，并对故障特征进行识别，测试样本为300，正确样本295，其诊断准确率为98.3333%。说明该方法在转子碰摩程度的识别中拥有较高的准确率。

5 结论

采用粒子群算法，通过合理地选择粒子群算法中的参数，获得了VMD中最优的参数模态分量个数K和惩罚因子α，SVM中最优的参数惩罚因子C和径向基核函数σ，弥补了VMD和SVM选取参数的不足，避免了人为设定参数的误差。同时支持向量机模型具有相对较高的模式识别精度。利用粒子群算法优化参数的方法在解决转子碰摩故障信号中具有一定的有效性和实用性。