基于Luenberger观测器PMSM无传感器控制策略

吕莹，石伟，林联伟，焦九顺

(1.株洲易力达机电有限公司，湖南株洲 412000；2.湖南工业大学交通工程学院，湖南株洲 412007)

0 引言

早在20世纪50年代，具有永久磁性的材料开始被引入到电机的研究中，永磁同步电动机凭借其优越的性能，具有高功率密度与转矩惯量比，同时还具有响应快、结构简单等特点，被广泛应用于工业及日常生活的各个领域，目前已是国内外研究的焦点[1]。

对于永磁同步电动机的传统空间矢量控制算法中，不可或缺的是对于电机转子位置的获取及转速的监测，对电机转子位置及转速的获取需要专门的传感器，如霍尔传感器，但传统的传感器安装和维护较复杂，增加了系统的复杂性从而使其可靠性降低[2-3]。因此使用可测量的物理量来计算电机转子位置及速度的方法受到广泛关注，成为研究的重要方向。目前较为流行的基于空间矢量算法无传感器控制方法主要有:模型参考自适应法(Model Reference Adaptive System,MRAS)[4]、滑膜观测器法(Sliding Mode Observer,SMO)[5]、扩展卡尔曼滤波器(Extended Kalman Filter,EKF)等方法[6-7]。模型参考自适应法对于电机参数较为敏感，且自适应率的估算比较困难[8]；滑膜观测器具有高频运动特性且有较强的鲁棒性，但存在抖振问题[9]；扩展卡尔曼滤波器算法比较复杂，同时对电机参数敏感[10]。由于Luenberger观测器具有动态响应快、估算精度高的优点，本文作者探讨一种基于Luenberger观测器的方法进行电机转子位置及转速的估计。

1 永磁同步电机数学模型

永磁同步电机的定子铁芯空间三相对称，因此在通入三相时间对称的正弦电流iA、iB、iC后形成一个旋转的磁场，磁场旋转的角速度与通入的电流频率相等。该磁场吸引贴在转子上的异性磁钢片，驱动电机转子转动。

Clarke变换是将三相静止坐标系(a-b-c)变换为两相静止坐标系(α-β)，经过Clark变换后得到两相静止坐标系下的定子电压uα、uβ为：

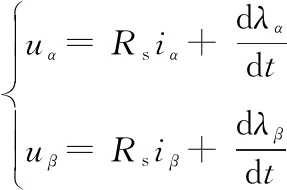
(1)

式中:Rs为定子电阻;iα、iβ分别为在两相坐标系下的定子电流;λα、λβ分别为在两相静止坐标系下的励磁绕组磁链，可用式(2)表示：

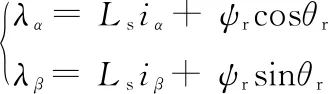
(2)

式中:Ls为定子的等效电感;ψr为永磁体磁链;θr为转子的位置角度,且可使用式(3)表示：

θr=pωrt

(3)

式中:p为电机磁极对数;ωr为转子角速度;t为时间。

将式(3)代入式(2)中，式(2)代入式(1)中，可得到：

(4)

由此得出永磁同步电机的状态方程为：

(5)

定义永磁同步电机的反电动势为：

(6)

由此可得出永磁同步电机的数学模型为:

(7)

2 电机转子位置与转速的估计

2.1 Luenberger观测器设计

Luenberger观测器具有一个含有输入变量的反馈环，主要是根据所观测系统的输入信号和输出信号，估计系统的内部状态，再重构出所观测的对象。在永磁同步电机的无位置传感器控制系统中，关键在于对电机位置角度的提取。通过对永磁同步电机的数学模型分析，在α、β坐标系下的反电动势包含了转速及电机转子位置角度的信息，因此被观测对象为永磁同步电机模型，其相对应的观测器模型如图1所示。

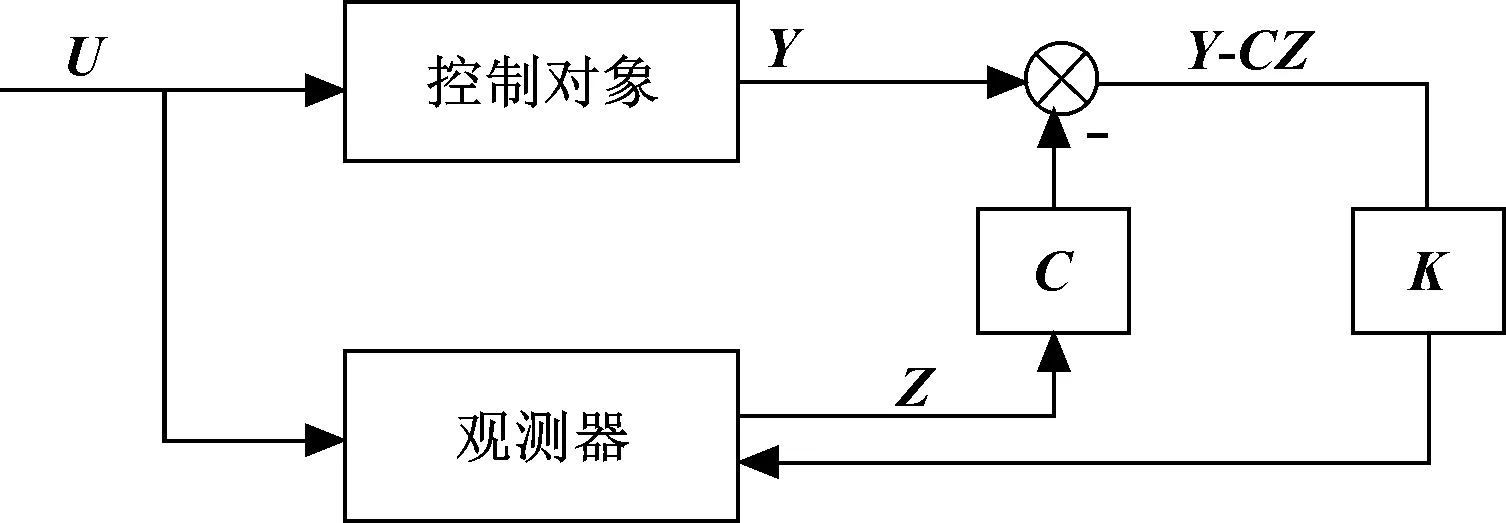
图1 永磁同步电机观测器模型

图中U为被控对象的输入，Y为被控对象的输出，Z为观测器的输出，定义观测器状态方程为：

(8)

为了方便构建观测器系统，选取状态变量x= [iαiβeαeβ]T，控制变量u= [uαuβ]T,输出变量y= [iαiβ]T。将电机的数学模型写为矩阵形式，因此得到永磁同步电机的状态方程：

(9)

对应系统的状态矩阵:

输入矩阵:

输出矩阵:

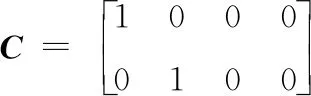
为满足观测器的构造条件，假设电状态变化量远大于机械状态变化量，即认为在很短的一段时间内，电机的转速是没有发生变化的，假设pωr是一个常数，对应的观测器模型为：

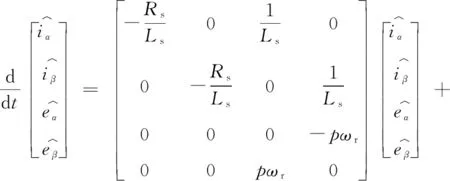
(10)

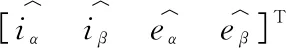
得到观测器的状态矩阵为：

(11)

为使Luenberger观测器渐进稳定，状态误差随时间变化趋近于零，根据李雅普诺夫第一法，使观测器的状态矩阵的所有特征值具有负实部，确定K1、K2的取值范围，文中不再详细描述。但为了加快观测器的收敛速度，并尽可能抑制噪声干扰，还需对K1、K2的值进行调整。

2.2 转子位置和转速的估算及锁相环系统

(12)

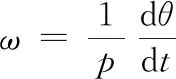
(13)

锁相环(Phase Locked Loop,PLL)实质是一个PI控制器，参考输入为Δθ，经过PI调节作用求出电机转速ω，再通过对ω进行积分得到电机转子位置角θ。锁相环中不包含正切计算，避免了由于某些特殊角度带来的计算误差，不包含微分环节，一定程度抑制了噪声干扰。锁相环的原理图如图2所示。

图2 锁相环估算原理框图

3 Luenberger观测器永磁同步电机控制系统

永磁同步电机的控制系统主要包括DC逆变电路、采样电路、SVPWM算法、电机位置估算以及电机本体，其控制系统框图如图3所示。

该控制系统中包含速度环和电流环双闭环系统，首先通过采样电路获得永磁同步电机的三相电流后，经过Clark变换得到静止坐标系下的α和β电流，再通过Park变换得到旋转坐标系下的d轴和q轴电流，有利于PI控制器的使用，通过PI调节减小d、q电流及电压，再经过反Park变换和反Clack变换最终输出PWM占空比到DC逆变器中，经过逆变器控制电机旋转。

图3 PMSM无位置控制系统框图

由图3可知，Luenberger观测器的输入为经过Clack变换后的两相静止坐标系的定子电压及定子电流，经过Luenberger及PLL估算电机α、β反电动势eα、eβ,根据反电动势可以计算出电机转子位置信息及电机转子的转速。

4 Simulink仿真及结果分析

在图3所示的系统框图的基础上，结合文中对Luenberger观测器的分析计算，使用Matlab&Simulink搭建基于Luenberger观测器的永磁同步电机无位置传感器控制系统，系统模型如图4所示。系统主要包括永磁同步电机本体、逆变电路模块、Clark变换及Park变换、Lunberger观测器估算、SVPWM模块，其中在Luenberger观测器模块中包含PLL模块用于估算电机转子的位置及转速。

图4 无传感器电机控制系统仿真模型

设定电机的主要参数为：极对数p= 4;定子电阻Rs= 1.132 Ω，定子电感Ls=Ld=Lq= 0.001 572 H;转子磁链ψr= 0.158 51 Wb。给定需求转速为600 r/min，电机负载为2 N·m。经过观测器估算的α、β的反电动势eα、eβ如图5所示，由图可知，eα、eβ比较平稳，没有异常波动。

图5 估算反电动势eα、eβ仿真波形

图6和图7分别为基于Luenberger观测器估算的电机转子的转速与实际测量转速对比图及转速的估算值和实际值的差值。

图6 转子转速的估算值与实际测量值仿真结果

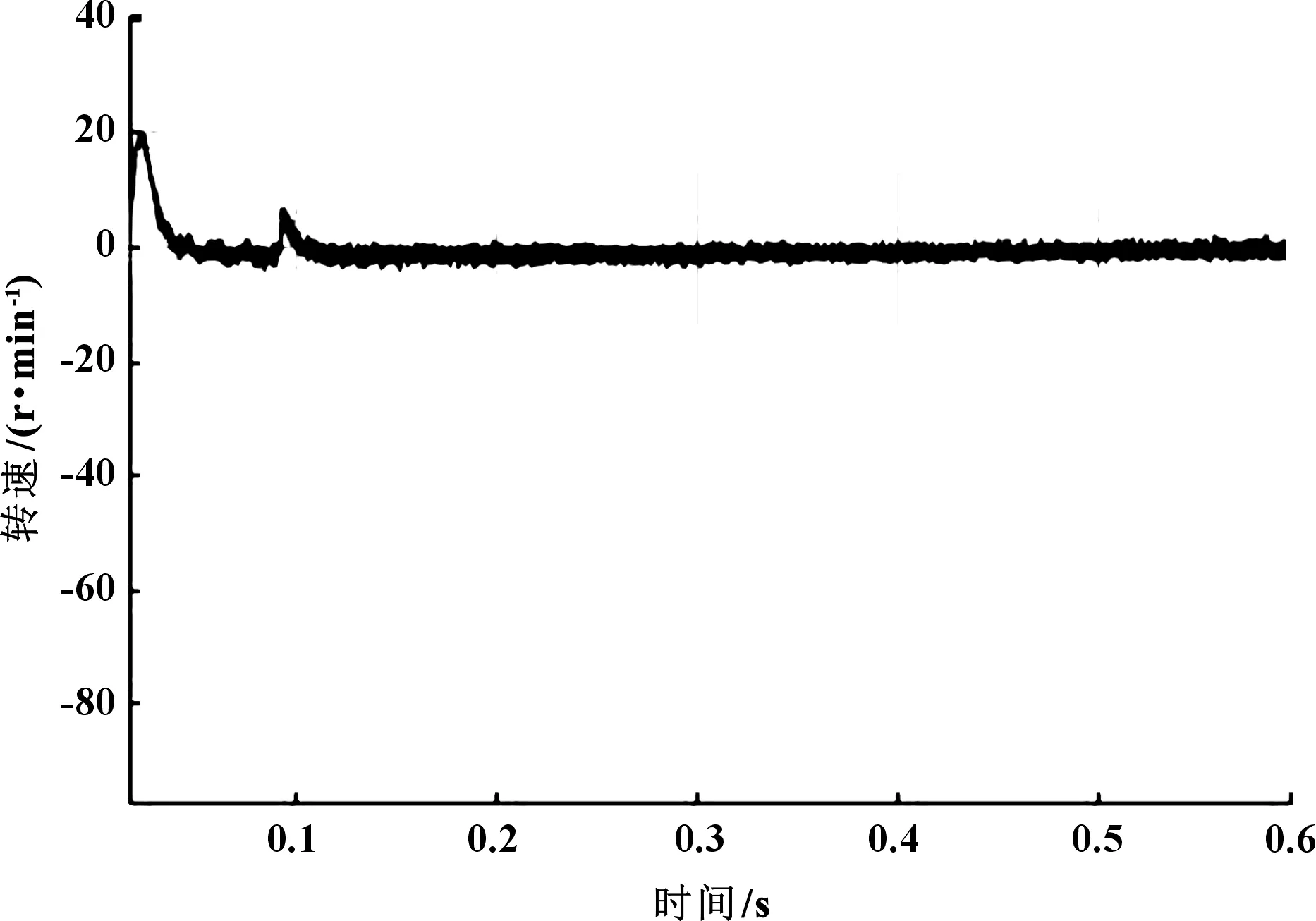
图7 转速估算值与实际测量值的差值

由图可知，估算转速与实际测量转速相差不大，基本一致。在约0.1 s时达到了需求转速，转速爬升过程也较为平稳，没有出现发散震荡现象。图8为电机转子的估算位置与实际位置的仿真结果。由图8可知电机转子的估算位置与实际测量的位置基本较为吻合。

图8 转子位置的估算值与实际位置仿真结果

在0.3 s时将电机负载由2 N·m阶跃至4 N·m，观察负载突变对于转速的影响，转速的测量值与估计值如图9所示，测量值与估计值的误差如图10所示。

图9 负载改变时电机转速测量值与估算值波形

由图9和图10可知，在0.3 s负载发生变化时，电机转速发生波动，且此波动经过Luenberger观测器的计算被放大，转速的估计值也产生波动，但随后很快收敛达到稳定,稳定后转速误差在5 r/min左右。表明系统可控且响应较快。

当负载发生变化时，电机的电磁转矩出现轻微抖动，但在0.04 s内收敛稳定，表明系统的负载能力良好。电磁转矩波形如图11所示。图12为负载改变前后的角度估算图，对比图8恒定负载的情况下基本没有变化，说明电机负载的变化对转子位置的影响不大，系统比较稳定。

图10 负载改变时转速测量值与估计值误差

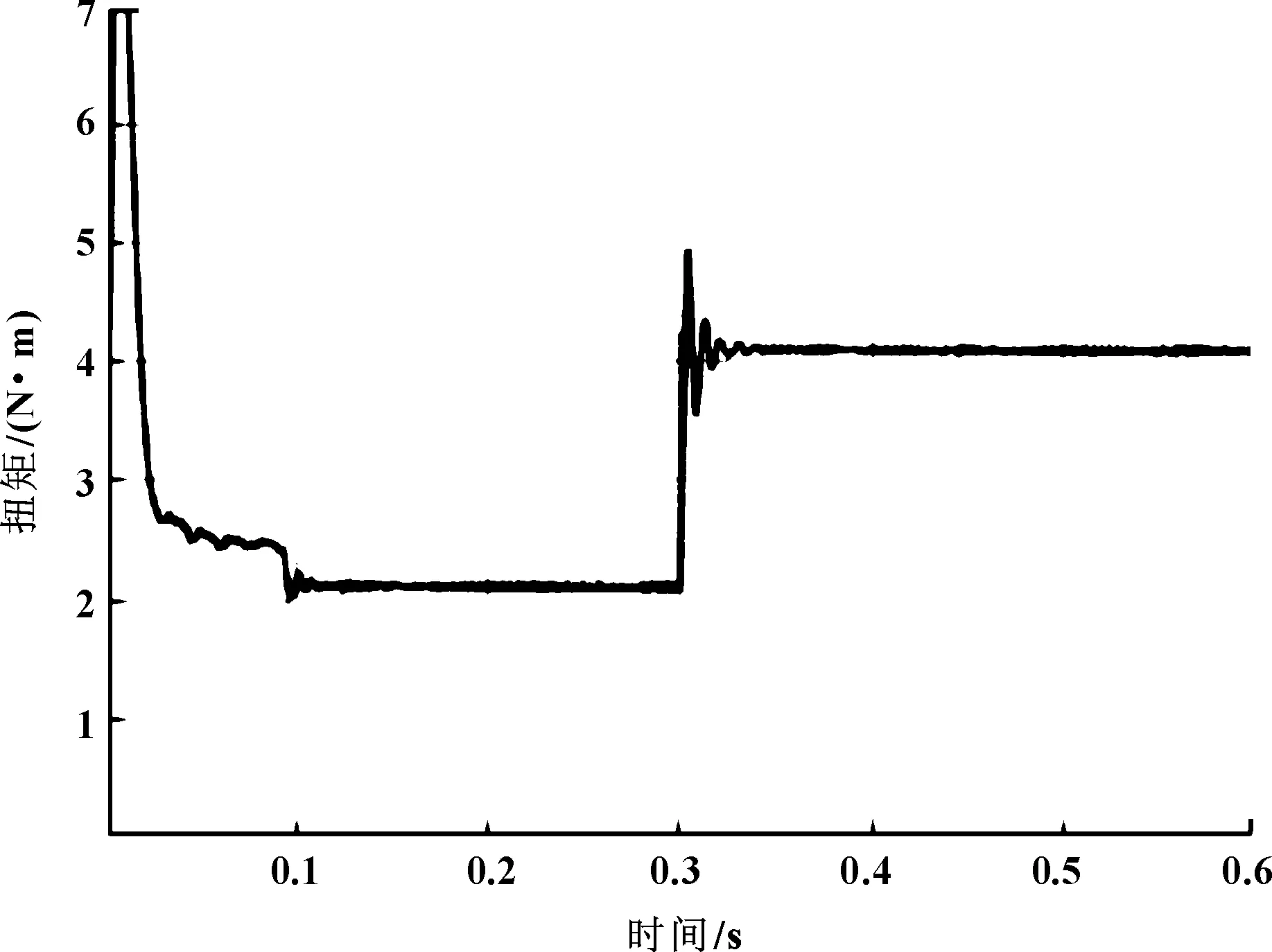
图11 负载改变时电机电磁转矩波形

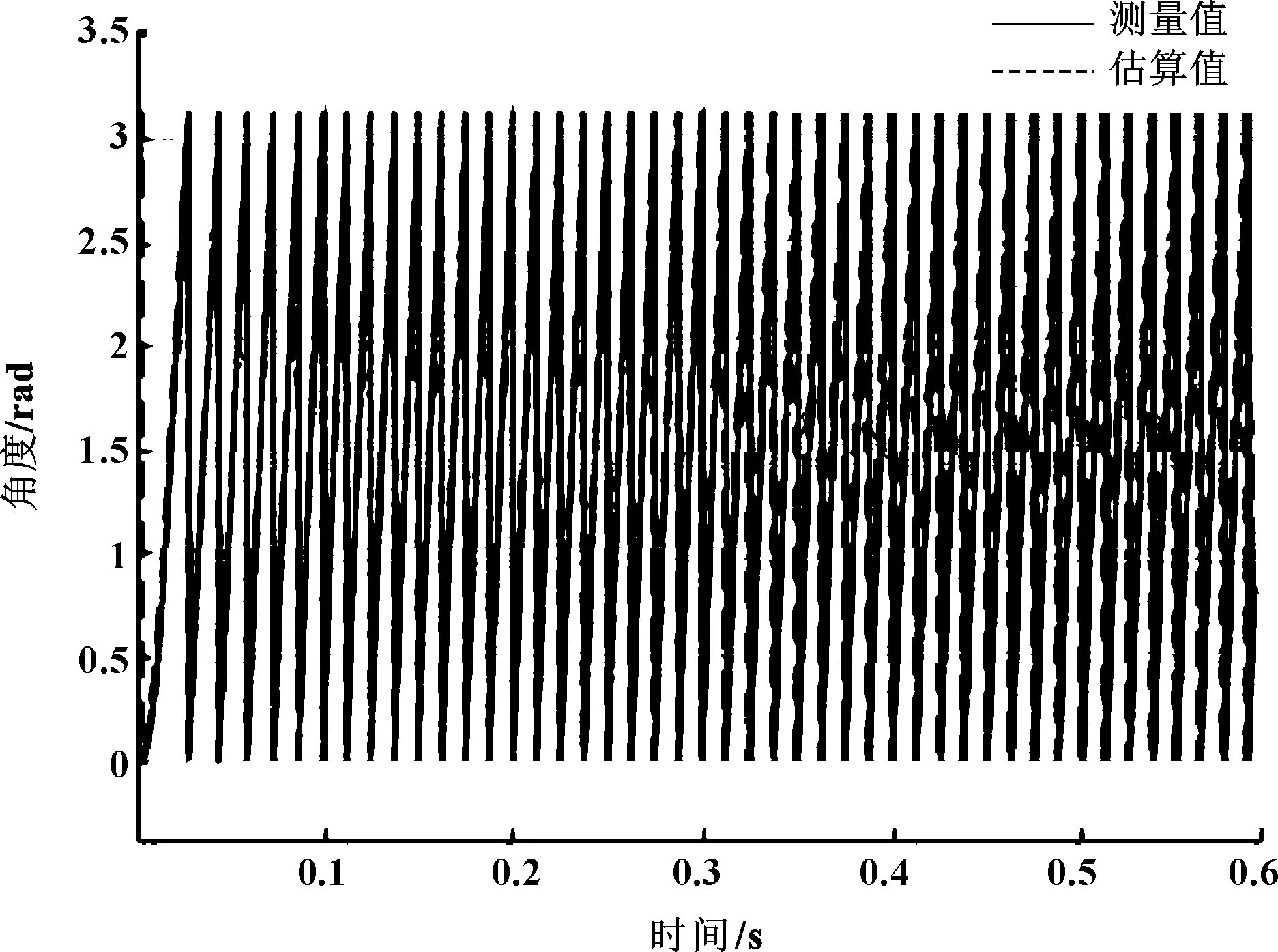
图12 加负载时电机转子位置测量值与估算值波形

5 结论

文中简单地描述了永磁同步电机的数学模型，阐述了Luenberger观测器的基本原理，并结合二者搭建Luenberger观测器。使用Luerberger观测器模拟永磁同步电机，并观测不可测量值，如α、β的反电动势，从反电动势中提取有关电机转子位置的信息，为避免反正切计算带来较大的误差，同时避免由于微分环节可能带来较大的噪声干扰，文中引入PLL对电机转子位置进行估算。通过使用Matlab&Simulink对该控制系统进行仿真，可知电机转子位置的估计值与实际值基本吻合，但转速随电机负载的改变波动较大。Luenberger观测器是通过对电机的反电动势进行观测从而得到转子位置信息，当电机转速较低时，反电动势较低不易观测，对转子位置的估算误差较大，因此对于Luenberger观测器在电机低速运行时的估算需要进行进一步优化。