高等数学课程教学策略研究

朱四如 陈兰花

【摘要】针对现行高等数学教学中存在的痛点问题，立足以学生为主体、教师为主导的现代教育理念，基于高等数学知识体系结构脉络和学情分析，笔者提出了适应课程教学的策略设计方法，通过丰富课堂教学形式、充分激发学生的学习兴趣和发挥学生的主体作用等方式，有效突破教学难点，提高课程教学效果，对数学课程教学具有一定的参考意义.

【关键词】教学痛点;激发兴趣;主体作用;问题牵引式教学

“高等数学”是大学理工类各专业在基础阶段的一门重要的必修课，是学生后续学习相关课程的基础，是培养学生逻辑思维能力和抽象思维能力的重要途径，也是培养学生科学研究方式的重要载体和提高人文素质的重要补充.一直以来，由于本课程知识内容多、理论性强、逻辑严谨，并且教学安排密度较大，高等数学教学中存在以下几个痛点：一是学生的学习方法不当、缺乏自主性，因为课程注重知识理解、自主学习，所以以往多做题、少思考的学习方式已不适应现行的高等数学学习，导致刷题的效果欠佳.二是课程内容抽象、理解困难，因为课程知识抽象，知识之间的逻辑联系强，学生一旦掌握不好某一知识点，就容易导致对后期知识理解困难.三是学用脱节、学不会用，因为传统的教学模式中偏重理论讲授，所以学生用所学数学解决实际问题的意识和能力明显不足.

本文针对现行教学中存在的几个痛点，力求通过全面分析和合理设计来破解难题，具体做法包括：首先，优化课程结构，厘清知识体系;其次，充分分析现在学生的学习特点，提出科学合理的教学策略;最后，给出相关建议，力求提高教学效果.

一、课程分析

（一）内容结构

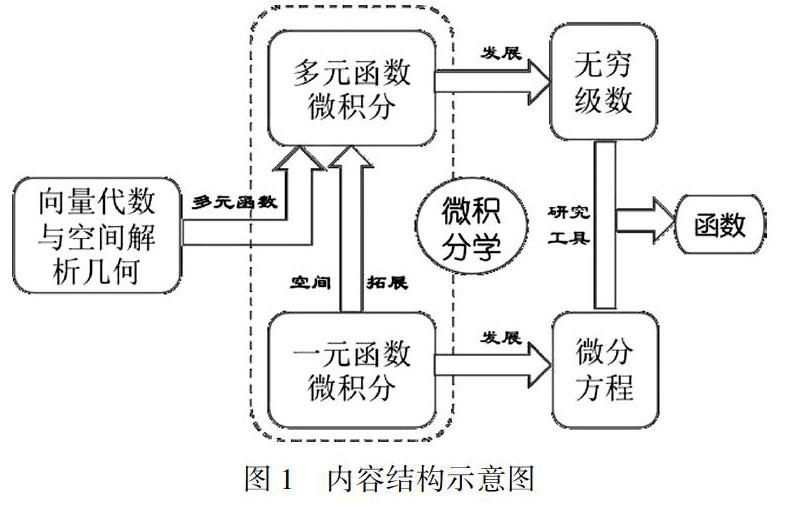
高等数学课程内容主要包括一元微积分学、微分方程、向量代数与空间解析几何、多元微积分学和无穷级数五大模块，因专业需求的不同，可能略有差异.理工科所学的高等数学内容结构一般如图1所示.

一元微积分学的研究对象为一元函数，涉及内容主要包括函数与连续、一元微分学、一元积分学，其中，函数与连续是构建高等数学中最重要的极限方法;一元微分学解决导数与微分的概念建立及其计算，为导数提供研究函数的基本工具——中值定理，以及用导数和微分研究函数的具体应用方法;一元积分学包含微积分的精华——牛顿-莱布尼茨公式，主要解决不定积分和定积分的计算，以及定积分的应用问题.微分方程是一种利用微积分知识寻找未知函数的重要方法，主要解决自然科学和工程技术领域中一些常用微分方程的解法.向量代数与空间解析几何是中学平面几何知识的推广，是学习多元微积分学必不可少的基础.多元微积分学的研究对象是多元函数，主要建立多元函数微积分学的概念、实际应用等问题.无穷级数是高等数学的重要组成部分之一，是一种表示函数、研究函数的重要工具.

高等数学课程各部分之间的逻辑关系是：一元微积分学和多元微积分学统称为微积分学，是高等数学课程的主体.多元微积分学是一元微积分学在空间上的拓展，多元微积分学的概念、公式和方法是一元微积分学相关内容的拓展.一元微积分学在拓展的过程中必须要用到多元微积分学的知识，因此向量代数与空间解析几何也是多元微积分学的重要基础.而微分方程和无穷级数正是由微积分学发展而来的研究函数的重要工具，是相对独立的两块内容.

（二）教学重难点

由以上分析可知，一元微积分学是除“向量代数与空间解析几何”以外所有内容课程的出发点，微积分学最重要的思想方法都在该部分得到了具体体现，因此成为教学的重点.多元微积分学需要较强的空间想象能力、扎实的一元微积分学基础和较强的计算能力，因此成为教学难点.基于把握重点、突破难点的原则，笔者建议把一元微积分学安排在第一学期进行教学，用于夯实学生的基础，而把其他内容安排在第二学期进行教学，这样可以体现知识学习的渐进性.

二、学情分析

随着国家教育新战略的实施和高考制度的改革，现在学生的综合素质普遍得到了提高，但是对于刚入学的大学生来说，高等数学是他们入学阶段遇到的第一个“拦路虎”，

须格外重视.这些大学生具有以下几个特点：

一是在知识上，学生的文化基础整体较好，但各地区高考的数学和物理要求有所差异，导致部分地区学生对三角函数、极坐标和参数方程等数学基础内容掌握得不好，同时物理基础不够扎实.二是在态度上，学生的学习目标不明确，缺乏持之以恒的定力，只要学习中稍有难度，就会产生畏难情绪，对相关知识满足于一知半解，缺乏严谨治学的科学态度.三是在方法上，学生的中学痕迹较重，重做题不重思考，沉迷于题海战术，自主学习的意识和能力较差，不能进行有效的知识归纳和总结，知识体系混乱.四是在知识获取能力上，现代技术成为学生的明显优势，学生都是信息时代的年轻人，有活力，接受新知识快，通过互联网获取信息的能力强.因此，在合理设计的基础上，教师可以充分借助丰富的网络资源和多元的信息教育技术进行教学.

三、实施策略

基于以上课程分析和学情分析，高等数学教学可进行以下针对性教学设计.

（一）教学策略设计

1.充分激發学生的学习兴趣.兴趣是最好的老师，浓厚的学习兴趣是推动学生学习的有效原动力.在课堂教学中，教师可通过融入数学发展历史、创设问题情境等方式，把数学知识注入灵魂，激发学生的学习兴趣，也可通过理论联系实际问题，培养学生的学习兴趣.

2.充分发挥学生的主体作用.教的最终目的是不教，因此，教师要创造一切条件为学生的“学”架桥铺路.在课堂教学中，教师可通过开展问题牵引式教学，将知识点进行合理分解，引导学生自主学习、合作探究和汇报展示，充分体现学生的主体地位.

3.充分利用信息技术.教师将现代信息技术与高等数学课程教学相结合，既能充分发挥现代信息技术的优势，又能提高课堂教学效率.教师可以利用多媒体技术，根据教学内容，通过声、形、动等创设出能对学生产生直接刺激的情境，激发学生探求新知的欲望，也可以运用多媒体技术把抽象的内容转化为学生熟悉的形象，把静态的知识转化为动态的图像，帮助学生更加清晰完整地认识知识.

（二）教学方法设计

基于课程特点，高等数学教学主要以启发式教学法为主，因此，本文在此基础上力求创新，依据上面的策略主要选取三种教学方法进行课程教学改革实施.

1.历史重现式教学法

在教学中，教师可紧扣知识发展脉络，从历史的角度再现伟大数学家们通过艰辛探索最终形成辉煌理论成果的完整过程，激发学生的学习兴趣，培养学生的探索欲望，从而提升学生的数学素质和人文素养.

例如，在教学“数列极限”这一知识点时，首先，为了帮助学生更好地理解极限思想和掌握数列极限的概念，教师从刘徽割圆术及祖冲之计算圆周率的问题出发，引出古代朴素的极限思想，增强学生的民族自豪感，达到教学融入课程思政的目标;其次，教师介绍17世纪以牛顿和莱布尼茨为代表的神秘极限观，提出需要解决的问题;然后，教师介绍达朗贝尔、柯西等人的探索性工作，让学生体会到科学研究的艰辛;最后，教师介绍维尔斯特拉斯给出的严谨的极限定义，让学生看到创新的重大意义.这样循着历史的脉络介绍极限能让学生体会数学思想产生的实际背景和过程，使学生对极限思想的本质有更深入的理解，同时能让学生体会到数学家们严谨求真、敢于质疑和勇于挑战的精神.

类似的还有“无穷小与无穷大”“导数的概念”“定积分的概念”等.教师可以通过引入数学历史发展进程，挖掘知识背后的精神内涵，激发学生的学习兴趣.

2.情境-问题-探究式教学法

根据教学内容和教学目的，教师可通过具有感染力的事物创设出隐含问题的情境.学生作为学习活动的主体，在教师的预设引导下围绕问题开展探究活动，通过亲身参与发现、探究、解决问题的全过程，主动构建包含在问题中的知识及科学探究的技能和方法.本教学方法的目的是激发学生的学习兴趣，使学生能主动构建知识体系，促进学生科学研究能力的发展和科学素养的提高.

例如，傅里叶级数内容抽象、推演严密，但其应用广泛，是相关数学理论分析的基础，尤其是电子工程、通信类相关专业后期课程学习的基础，因此，学生有必要学懂、学通.传统教学的效果不好，合理的设计是先通过设置“音乐去噪”的应用场景引出本课研究的课题，再逐步引出“如何将函数展开成傅里叶级数”“级数是否收敛于函数本身”等问题，进而得到本节课的核心结论.

类似的还有“导数与微分的应用”“积分的应用”“微分方程”等涉及具有实际应用意义的知识.在教学中，教师可通过设置情境逐步探究，在激發学生学习兴趣的同时让学生感受到数学就在身边，从而解决学不会用的问题.

3.问题牵引式教学法

这是一种以问题为导向的教学方法，又称为PBL（ProblemBased Learning）教学法，适合以一章知识或几章知识为单位，选取的问题通常具有一定的综合性.该教学方法注重理论教学和实践教学相结合，是将学生置于实际问题的情境中，以某一特定任务，引导学生通过小组讨论、合作探究等方式解决问题，在学习中促使学生自主查阅资料，主动寻求隐含于问题背后的科学知识，提高学生总结归纳、团队协作的能力，逐渐使学生具有探索精神和创新意识.

PBL教学法的总体设计一般分为以下几个步骤：第一，按照高等数学章节来梳理问题案例库和相应的背景阅读资料;第二，在教学之前，教师安排学生分组，以小组为单位布置任务，要求学生明确任务要求及时间节点;第三，学生自主查阅资料，以组内或组间形式自行组织研讨与交流;第四，通过结合信息化手段，教师适时介入指导，对学生进行针对性辅导答疑;

第五，小组汇报并接受其他小组学生的质疑和讲评.

例如，在教学“函数与极限”这一知识点时，教师可以布置“重要极限-种群增长模型”任务.一方面，通过执行上述总体设计步骤，

学生能联想到银行利率的问题，得到离散形式的复利计算模型，由离散思维拓展到连续思维，实现知识的顺利迁移和思维的升华，得到函数形式的模型;另一方面，通过这种方式，学生能理解其背后的实际背景，从而加强对知识的理解，感受到数学的魅力.类似的还有“易拉罐设计问题”“面积测定问题”等.

（三）特色创新

在遵循教学规律的基础上，以上所设计的策略和方法能充分分析教学对象的特点和教学目标，具有一定的创新性，主要体现在以下几个方面：一是通过融入数学史，教师能激发学生的学习兴趣，提高学生的人文素养;二是通过开展情境-问题-探究式教学，教师能激发学生的学习兴趣，提高学生科学研究的思维方法;三是通过探索PBL教学法，教师能培养学生的自主学习意识和应用数学的能力.

结 语

本文基于课程体系的教学设计，对知识脉络的厘清有一定的借鉴作用.本文的学情分析对教学策略的设计有针对性作用;本文的教学方法示例对教学组织的实施具有参考作用.教学有法、教无定法，在实际的教学中，教师应依据高等数学的知识特点和实际教学对象的学习特点，充分借助信息化技术，采用合适的教学方法，致力于淘汰“水课”、打造“金课”，努力提高教学效果.

【参考文献】

[1]张奠宇，李士锜，李俊.数学教育学导论[M].北京：高等教育出版社，2003.