具有瞬时与非瞬时脉冲效应的害虫综合治理切换模型研究
齐 琪,刘 兵
(1.辽宁师范大学 数学学院,辽宁 大连 116029;2 鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)
害虫治理始终是农业领域重要的研究课题,最常用的控制害虫的方法是化学控制和生物控制.近年来,许多学者利用脉冲微分方程将两种方法结合起来建立综合害虫治理模型[1-3],他们大部分假定杀虫剂的作用是瞬时成比例杀死害虫的.实际上,杀虫剂的作用会随着时间的推移而具有一定的残留作用[4-5].文献[6-7]利用两系统切换的思想研究了单种群灭绝的控制阈值.在此基础上,文献[8]提出一个具有瞬时与非瞬时脉冲效应的单种群阶段结构捕获模型.在害虫治理过程中,喷洒杀虫剂后,害虫和天敌会在瞬间被大量杀死,然后由于杀虫剂具有残留作用,对害虫和天敌的作用逐渐减弱,因此,用具有瞬时与非瞬时脉冲效应的数学模型去描述这种现象更为合理.本文在文献[1]的基础上,考虑到固定时刻喷洒杀虫剂和释放天敌,并且在杀虫剂喷洒以后,天敌对害虫的捕获率以及转化率的不同,建立一个具有瞬时与非瞬时脉冲效应的害虫综合治理切换模型,具体分析害虫灭绝周期解全局渐近稳定的条件.
1 模型建立
本文利用切换系统的思想,建立如下具有瞬时和非瞬时脉冲效应的害虫综合治理模型:
(1)
模型(1)中,x(t),y(t)分别表示t时刻害虫、天敌的种群数量;r>0是害虫种群的内禀增长率;K>0为害虫的环境容纳量;T是实施害虫控制策略的周期;0
2 害虫灭绝的阈值
首先,考虑下面的子系统:
(2)
引理1子系统(2)存在正周期解y*(t)并且对系统(2)的任何解y(t)都有:当t→时,y(t)→y*(t),其中
(3)
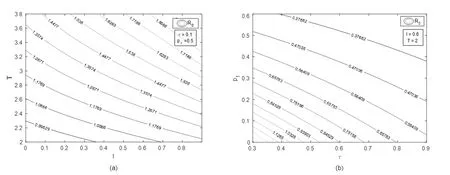
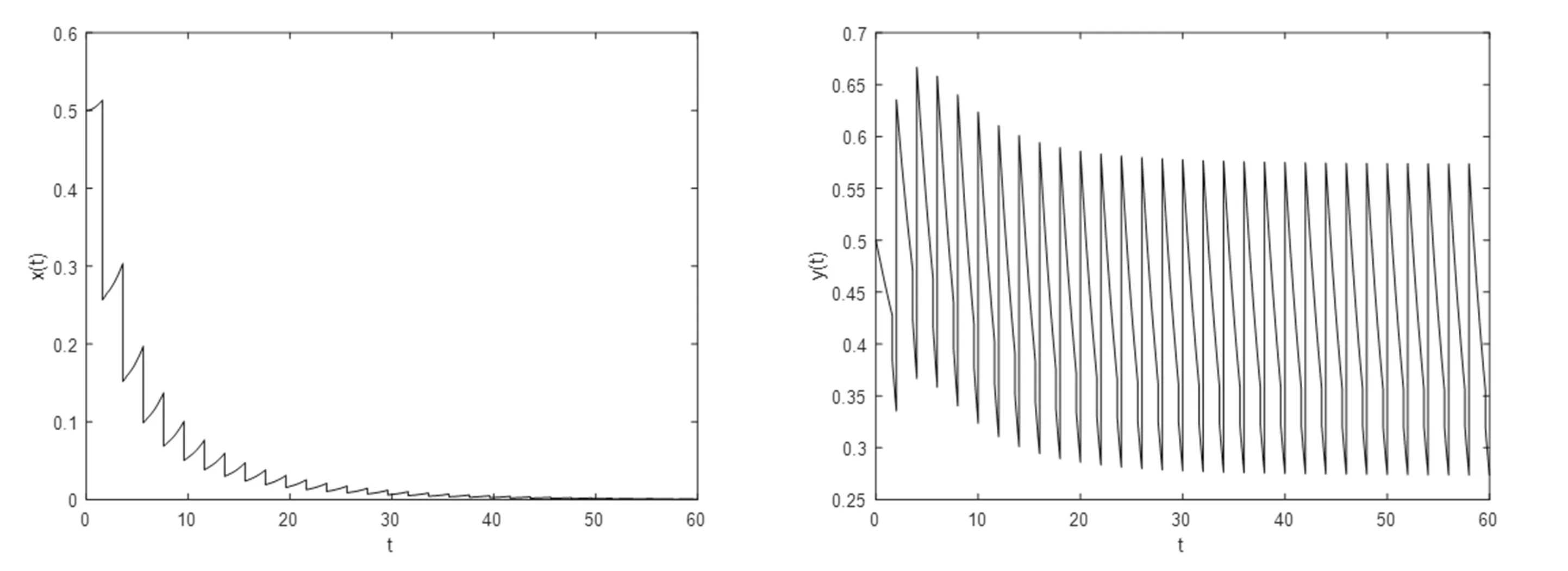
证明系统(2)在任意脉冲区间nT 在任意区间(n+l)T 则 令yn=y(nT+),则可得如下差分方程 此差分方程存在唯一正不动点 由于 因此,由差分方程理论可知,y*是此差分方程的全局渐近稳定的正平衡点,从而系统(2)存在一个全局渐近稳定的正周期解y*(t),当t→时,系统(2)的任意解y(t)→y*(t),其表达式如(3)所示. 定理1令 如果R0<1,则系统(1)的害虫根除周期解(0,y*(t))是全局渐近稳定的. 证明设(x(t),y(t))是系统(1)以(x(0),y(0))为初始值的解,系统(1)的周期解(3)的局部渐近稳定性可以利用系统的变分方程来确定.为此,作变换x(t)=α(t),y(t)=y*(t)+β(t),则相应的线性方程的解为 其中,Ψ(t)=Ψ1(t)·Ψ2(t),且Ψ1(t),Ψ2(t)满足 且Ψ1(0)=Ψ2(0)=I是单位矩阵,因此 由于在下面的计算中,没有用到(*),所以没有必要给出其确切表达式.由Floquet理论知,如果单值矩阵 的两个特征值的模小于1,则害虫灭绝周期解(0,y*(t))是局部渐近稳定的.实际上,其特征值分别为 系统(1)的周期解是渐近稳定的,当且仅当|λ1|<1,即R0<1. 下面证明系统的周期解的全局吸引性,由于R0<1,所以存在充分小的ε(ε>0),使得 成立. 从系统(1)的第二和第六个方程可得, 考虑如下脉冲微分方程 利用脉冲微分方程比较定理可得y(t)≥N(t),并且当t→时,N(t)→y*(t).因此,当ε(ε>0)足够小,t充分大时,不等式 y(t)≥N(t)>y*(t)-ε 成立.假设上式对所有t≥0成立,可得 由脉冲微分方程比较定理,当t∈(nT,(n+1)T]时, 由于χ<1,所以当n→,x((n+1)T)→0.因此,当t→时,x(t)→0. 下面证明:当t→时,y(t)→y*(t). (4) (5) 由式(4)和式(5)的左边不等式,可得y(t)≥N(t),并且当t→时,N(t)→y*(t).对于右侧,考虑如下比较系统: 由引理1知,当t→时,z(t)→z*(t),其中, 因此,对任意ε1>0,存在t2>0,使得当t>t2时,有y*(t)-ε1 所以,当R0<1时,系统(1)的害虫根除周期解(3)是全局渐近稳定的. 本文建立一个具有瞬时与非瞬时脉冲效应的害虫综合治理切换模型,通过理论分析,得到害虫灭绝周期解全局渐近稳定的充分条件.利用数值模拟,图1中(a)和(b)分别给出R0关于l和T的等高线,τ和p1的等高线,由图1(a)知,R0关于l和T都是单调增加函数,即R0随着喷洒杀虫剂时刻l的延后或脉冲周期T的增加而增大,可以看出尽早使用杀虫剂或缩短脉冲控制的周期有利于害虫治理.由图1(b)可以看出R0随着释放天敌数量τ或杀虫剂对害虫的瞬时杀死率p1的增加而减少,这表明增加天敌的投放量或选择对害虫致死率高的杀虫剂有利于害虫治理.图1中,其他参数取值为r=0.5,a1=0.5,a2=0.3,c=0.3,k1=0.8,k2=0.6,m1=0.2,m2=0.1,δ1=0.4,δ2=0.6,p2=0.1. 图1 等高线图 由图1(a)可知,当T=2,l=0.8时,R0<0.因此,由定理1知,害虫灭绝周期解是全局渐近稳定的(见图2),最终天敌种群y(t)周期性振荡,而害虫种群x(t)趋于灭绝.图2中,参数取值为r=0.5,K=1,a1=0.5,a2=0.3,c=0.3,k1=0.8,k2=0.6,m1=0.2,m2=0.1,T=2,l=0.8,p1=0.5,δ1=0.4,δ2=0.6,p2=0.1,τ=0.3. 图2 系统(1)害虫种群和天敌种群的时间序列图 本文没有考虑不同频率喷洒杀虫剂和释放天敌对害虫治理的影响,以及长期使用同一种杀虫剂害虫会产生抗药性的因素,我们将在以后做进一步的研究.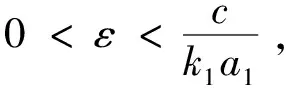
3 结论