一种基于组合形态学滤波的移相相减方法*

郑修才

（山东大学数学学院，济南 250100）

0 引言

受线列阵空间锥形指向性影响，单条线列阵在目标水平方位估计中存在左右舷模糊问题，为了解决该问题，研究学者率先提出依据搭载平台的机动特性，通过改变平台航向解决左右舷模糊问题，但该方法需要平台改变自身运动状态，影响目标方位估计连续性［1-4］。对此，研究学者再次提出利用双线列阵、三元水听器组线列阵、矢量水听器线列阵解决左右舷模糊问题，并收到了一定应用效果；在双线列阵应用中，常用方法为噪声相关模型方法、处理频带选择法、相关时延差法、几何相移模型方法等［5-8］。

噪声相关模型方法［9-10］依据双线列阵水听器拾取噪声相关性，构建出双线列阵噪声相关矩阵，得到最优波束加权系数，使左右波束具有心形指向性，进而解决左右舷模糊问题，由于该方法中最优波束加权系数与信号频率有关，对于宽带信号，存在一定计算量；处理频带选择法［11］依据双线列阵指向性函数左右舷抑制增益选择最优处理频带，进而解决左右舷模糊问题，但系统增益受最优处理频带影响较大，在特征频带小于目标信号带宽时，会削弱系统增益，影响方位估计效果；相关时延差法［12-13］依据同一目标信号到达双线列阵时间与方位关系，通过对双线列阵在镜像方位波束信号，提取求相关实现左右舷分辨，但该方法受双线列阵参考位置影响较大；几何相移模型方法分为移相相加法和移相相减法［14-17］；其中，移相相加法依据双线列阵左右相邻水听器拾取数据相关性，通过移相相加使左右相邻水听如同矢量水听器一样具有心形指向性，但该方法对左右相邻水听器间距有一定要求，间距较小时，心形指向性较差，不利解决左右舷模糊问题；同样，移相相减法也是依据双线列阵左右相邻水听器拾取数据相关性，通过移相相减使左右相邻水听如同矢量水听器一样具有心形指向性，该方法虽然降低了对左右相邻水听器间距要求，但会削弱端射方向波束能量，不利于端射方向目标方位估计。为了提高移相相减法对端射方向目标方位估计效果，文献［18-19］提出了通过能量补偿方式提升端射方向波束能量，改善了移相相减法在实际应用中的效果，但受修正因子影响较大。

针对几何移相相减法的端射能量衰减问题。依据形态学局部非线性变换特性［18-20］，本文首先采用组合形态学滤波方法提取空间谱基底，通过空间谱基底降低心形指向性函数对合成波束影响；然后采用动态规划实现对目标检测与轨迹提取［21］。理论推导分析和数值仿真结果均验证，在实现目标分辨中，相比原移相相减法，本文方法对最低信噪比的需求得到了3 dB 的降低，提高了移相相减法在实际应用中的稳健性。

1 移相相减法

1.1 数学模型

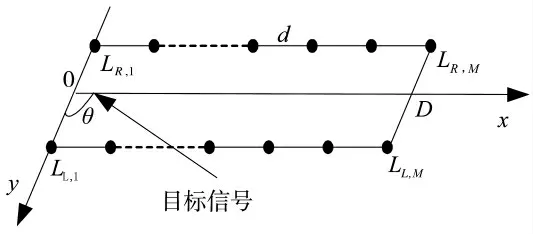
图1 双线列阵拾取目标信号模型示意图

为了能够将左右舷抑制比采用更为直观的方式表示出来，对式（2）进行平方处理，得到双线列阵在扫描方向θ0处输出波束能量为：

1.2 端射能量分析

虽然几何移相相减法通过移相相减可使左右相邻水听如同矢量水听器一样具有心形指向性，降低了对左/右线列阵相邻水听器间距要求，但存在端射方向波束能量衰减问题，不利于端射方向目标方位估计。

为了进一步说明几何移相相减法存在的端射方向波束能量衰减问题，在双线列阵左/右相邻水听器间距取不同值情况下，图2 给出了由式（3）所得不同方位波束能量归一化值。

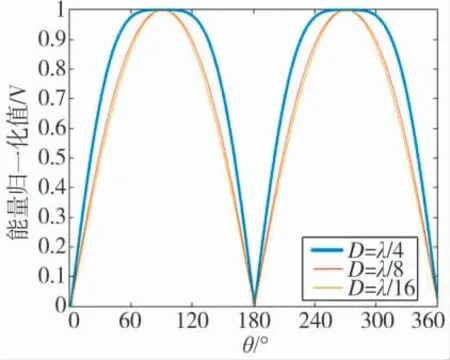
图2 几何移相相减法输出波束能量归一化值

另外，由图2 所示结果还可得知，对于非正横方向的同一方位上的同一目标信号，随着双线列阵左/右相邻水听器间距变小，式（3）输出波束能量存在微弱的减少。

所以对于移相相减法存在的能量衰减问题，另一种表述方式为：要实现对目标检测与判决，就需要一定的信噪比，即存在对弱目标检测与判决所需最低信噪比较高问题。

2 基于组合形态学滤波的移相相减法

2.1 形态学滤波

形态学滤波是基于随机集合论、积分几何论和拓扑逻辑论等非线性处理和分析理论，已广泛应用于图像处理领域［20］。本文采用其对移相相减法输出空间谱进行处理，利用预定义的结构元素对空间谱进行局部修正，修改空间谱局部特征，以达到提取目标信号、抑制噪声的目的，得到空间谱更本质的形态［20-24］。

2.2 基底提取

形态学滤波中腐蚀、开变换等同于局部最小值提取处理，由此可采用腐蚀、开变换估计出移相相减法输出空间谱基底，但受背景噪声影响，双线列阵输出空间谱中会存在由背景噪声形成的毛刺，这些毛刺将会对腐蚀、开变换产生影响，不利于对双线列阵输出空间谱局部最小值提取处理。对此，本文采用开、闭组合变换方法提取双线列阵输出空间谱局部最小值。

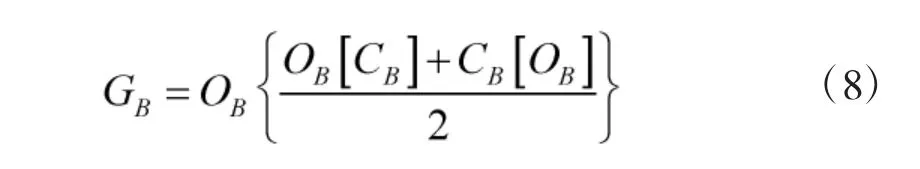
该方法联合了开、闭变换，并将变换进行了平均处理，然后再联合1 次开变换，经过多次形态学组合处理后，所得结果可很好地提取出移相相减法输出空间谱局部最小值，反映移相相减法输出空间谱基底，再按式（9）对移相相减法输出空间谱进行补偿处理，降低能量衰减对弱目标检测与判决造成的影响。

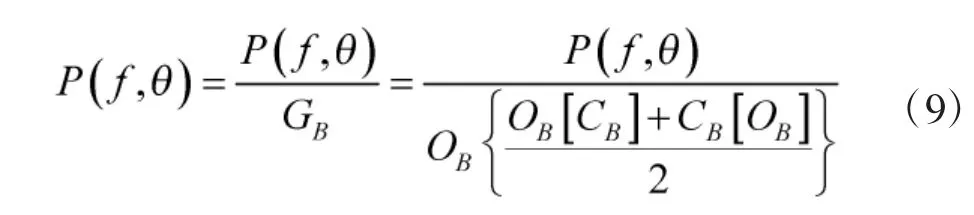
2.3 目标轨迹提取

动态规划是解决多阶段决策问题最优化的一种方法。该方法可将多阶段复杂的决策问题划分为简单的一系列单阶段决策问题，在各阶段对所需决策问题寻取最优解，从而使最终决策达到全局最优，即当各阶段决策确定后，形成了1 个决策序列，进而确定了状态变量在整个过程中的1 条活动路线［25］。对组合形态学滤波补偿后的空间谱，按图3所示流程进行目标检测与轨迹提取。

具体过程如下：

1）初始化

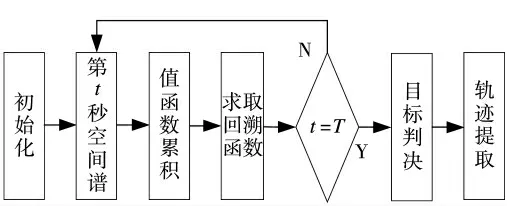
图3 目标检测与轨迹提取流程图

令回溯函数为0，读入第1 s、第2 s 双线列阵输出空间谱，假设第2 s 双线列阵输出空间谱某点方位为x2，则其在第1 s 双线列阵输出空间谱中对应邻域为Ax2（Ax2大小由目标方位变化范围决定），计算Ax2各方位转移至方位x2处的能量累积。将x2遍历整个空间谱所有扫描角度，得到值函数累积结果。

2）递推累积

如图4 所示，读入第t 秒空间谱，在第t 秒和第t-1 秒中各有一个方位xt和xt-1。xt-1位于xt在第t-1秒的邻域Axt中。对xt和xt-1计算值函数能量累积，选择值函数最大的作为xt-1到xt的最优路径，并将其记录到第t-1 秒回溯函数；同时，在各自范围内进行遍历。

3）目标判决

当t=T，T 为动态规划预设长度值，比较终点各方位位置处值函数累积结果，并将累积结果与判决阈值进行比较，将超过判决阈值的值函数设为目标。

4）轨迹提取

对于超过判决阈值的值函数，令t=T-1，T-2，…，1，回溯目标方位路径，该路径即为目标轨迹。

图4 各时刻空间谱递推累积示意图

3 数值仿真分析

为了验证本文所述方法可有效解决移相相减法存在的端射方向波束能量衰减问题，降低移相相减法对最低信噪比的需求，提高移相相减法在实际应用中的稳健性。以下进行数值仿真分析。

按图1 所示双线列阵模型为例，并令d=8 m，N=32，D=1 m，双线列阵系统采样率为fs=5 000 Hz，背景噪声为高斯白噪声，服从N（0，1）分布，1 运动目标位于双线列阵左舷侧，目标信号为高斯信号，服从N（0，1）分布，目标信号和背景噪声带宽均为f=20 Hz～100 Hz，目标信号与背景噪声输入信噪比为SNR。图5 为SNR=-20 dB～0 dB 情况下，两种方法通过500 次独立统计所得目标检测概率。图6～图8 为在SNR=-16 dB 情况下，两种方法所得方位历程图和空间谱。

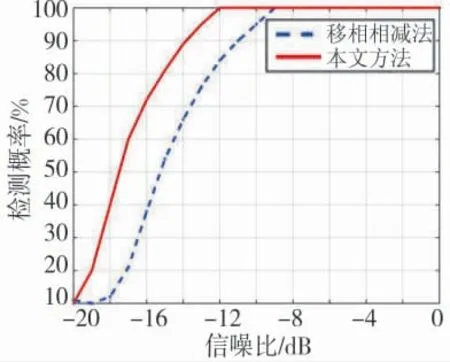
图5 两种方法所得检测概率

图6 移相相减法所得方位历程图

图7 本文方法所得方位历程图

图8 空间谱

由图5～图8 可知，在该仿真条件下，对于同一检测概率情况，相比移相相减法，本文方法对最低信噪比的需求得到了3 dB 的降低；在保持对目标分辨情况下，在移相相减法无法有效实现对目标检测情况时，通过组合心态学滤波和动态规划，有效实现了对目标检测和方位轨迹提取，降低了移相相减技术对最低信噪比的需求。

4 结论

针对移相相减技术对弱目标检测与判决所需最低信噪比较高的问题，首先推导了移相相减法合成波束函数；然后依据数学形态学局部非线性变换特性和局部最小值提取技术，提出了一种基于组合形态学滤波的移相相减方法。理论推导分析和仿真实验结果均表明，在移相相减法无法实现对目标检测和轨迹提取情况时，本文方法通过组合形态学滤波和动态规划，有效实现了对目标检测和轨迹提取。