射频/红外波束复合器边齿设计与分析方法
田 义,王超峰,李艳红,张 励
(上海机电工程研究所,上海 201109)
0 引 言
为了研制、开发和验证射频/红外双模共口径复合制导系统,需要进行大量复杂的仿真试验。半实物仿真技术能够有效地弥补数字仿真或外场试验的诸多不足:相比数字仿真,其结果更加真实可信;相比外场试验,其试验过程及环境可控性好,系统重复性好,能够获得更全面的数据,能完成外场无法实现的试验[1]。射频/红外共口径复合制导控制半实物仿真技术比单模复合制导控制半实物仿真技术更加复杂,实现更加困难[2],需要射频目标辐射的电磁波束与红外目标辐射的光束在空间上进行同向复合形成射频/红外共口径复合目标。能实现上述功能的射频/红外波束复合器是复合制导半实物仿真系统的关键。波束复合器件通过透射一个波束同时反射另一个波束实现两个波束的复合,通常透射射频波束反射红外光波[3]。当波束复合器的尺寸大到覆盖入射电磁波束的波束宽度时,波束复合器边缘作用不明显,不会对入射场产生影响。对于半实物仿真系统,入射波束往往通过满足远场条件的天线辐射,入射波束可视为平面波,波束宽度远远大于波束复合器的口径,波束复合器边缘起到了空间介质截断的作用,即造成照射到波束复合器内部和照射到波束复合器外部的电磁波传播路径不一致。这种情况下波束复合器的边缘效应就会显现,表现为边缘绕射波与透射波形成干涉造成工作区场分布的起伏,即均匀性下降。
为了改善场分布的均匀性,当入射波束宽度有限时,可增加波束复合器尺寸,当波束复合器尺寸足够大,边缘将趋近于无限远离入射波束,边缘绕射效应将会逐渐降低[4-5]。然而,增大波束复合器的尺寸会增大工程实现的难度。通常情况下,波束复合器的尺寸受到半实物仿真系统布局的约束,难以增大。为了在有限尺寸下降低边缘绕射效应,一种可能的方法是对入射场的幅度沿径向进行切削,即通过卷边、边齿等手段使得入射场越靠近边缘能量越弱,同时打散绕射波的传播方向,使得工作区内难以形成能量较大的干涉波,等效的边缘效应也就越弱,该方法已广泛应用于紧缩场测试暗室的反射抛物面边缘处理,用于改善场的均匀性[6]。对于紧缩场测试暗室,其馈源单一且固定,入射电磁波的波束分布已知且入射角度固定,可以较容易地进行边齿结构设计。然而,对于半实物仿真系统,波束复合器与紧缩场测试暗室中的反射抛物面不同,主要表现在入射波为远场,且入射角连续可变,这就对波束复合器的边齿设计带来了挑战[6-11]。
为此,本文提出了一种针对波束复合器基于几何绕射理论和口径场积分的边齿设计与分析方法。利用Keller衍射定律,设计边齿形状,避免将入射波经边缘绕射的出射波进入工作区,进而影响场的均匀性。为了获得工作区内因边缘绕射引起的空间场分布,基于口径场积分理论,将忽略波束复合器内部细节结构,等效边缘口径。对于与半实物仿真系统电轴垂直安装的全息型[12]、微镜阵列型[4,13]波束复合器,口径等效为边缘内部区域。对于与半实物仿真系统电轴非垂直安装的波束复合器(例如:频选表面型[14-15]、网栅型[16]、多层介质平板型[17]等),波束复合器的边缘轮廓可以投影到半实物仿真系统中与电轴垂直的面,使得工作平面与等效口径平行[11]。由于直达波和绕射波传播路径不同,通过对空域场分布的域变换,在时域和角频域可以较容易地区分直达波和绕射波,以便分析边齿处理对绕射波的影响[9,11]。
1 边齿设计方法
波束复合器被分为两个区域,如图1所示。一个边长为D的正方形区域由方形部分的中心区和n个三角形构成的边齿区组成。边齿区中每个三角形的高度和宽度分别为h和l,中心区的宽度为D-2h。工作区是放置被测设备的区域,这里设计为一个半径为r的圆形区域。工作区和波束复合器之间的距离定义为dQ。波束复合器的工作频率是f。在坐标系xS-oS-yS下用极坐标定义入射角,入射角极向最大值是θMAX,极角θS从0°到360°可变。待设计的参数为h、n以及每个边齿的角度θE。
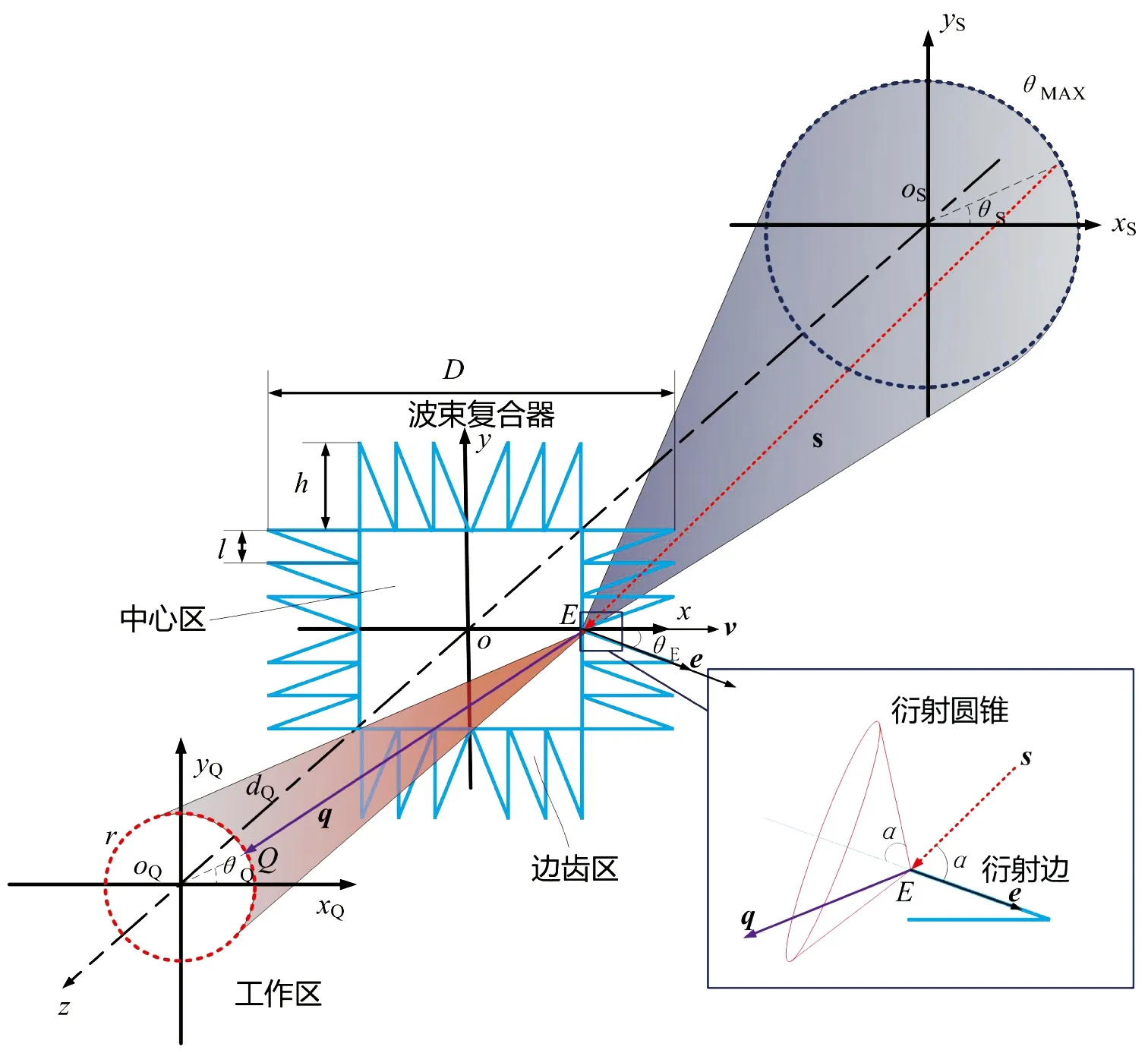
图1 边齿设计原理示意图Fig.1 The principle of serrated edge design method
第一步,可以根据等效梯形幅度切削设计h,边齿的一个作用可视为对入射场实现了幅度切削。在保证入射波相位不变的同时使得入射波的幅度满足梯形分布,切削靠近边缘的场幅度分布的同时保持中心区场分布的均匀性,可有效压制散射场。幅度切削可通过在波束复合器表面按照切削公式镀制或贴敷不同厚度或吸波系数的吸波材料来实现[18-20]。切削系数T可以表示为
(1)
当h过大时,中心区会变小,对中心区的场幅度进行过度切削,会增大透射波的场的非均匀性;当h过小时,边齿区的幅度切削作用将变得不明显,无法实现有效的边缘绕射抑制作用。因此必定至少有一个最优值h,使得场的均匀性最优。
第二步,找到最优解h后确定边齿的倾角。如图1所示,中心区的右侧边缘某一点E在x-o-y坐标系下记为(xE,yE,0),被入射电磁波s= (sinθMAXcosθS, sinθMAXsinθS, cosθMAX)照射。在E点处定义单元矢量e=[cosθE, sinθE, 0],其中θE是矢量e和法线v的夹角。而α则是s和e之间的夹角,即
(2)
如果s沿着θS扫描将生成一个圆锥,按照Keller衍射定律[10,21],边缘的衍射辐射波仍是一个与α相等的圆锥面,如图1所示,且α存在一个最小值αMIN。类似地,如果点Q(rcosθQ,rsinθQ,dQ)沿工作区的边以θQ旋转,则被矢量q扫过的曲面仍会是一个圆锥。定义β是q和-e的夹角,可以表示为
(3)
为此,就会存在一个β的最大值βMAX。如果αMIN大于βMAX,衍射波就不会进入工作区。可允许的θE的范围应当由条件αMIN>βMAX确定。最后一步是通过场的均匀性分析,找到最优化的n值。这3个参数确定后,边齿的结构也将被确定。
2 口径场积分场均匀性分析方法
按照等效原理,场分布可以通过计算口径内的等效辐射源的辐射场获得[7-9,11]。依据傅里叶变换原理,任意复杂的电磁波可以展开为不同平面波的叠加。入射平面波Ein的入射角的幅度为θ,相位角为ø,口径场EA可以表示为[22-23]
EA(x,y)=T(x,y)Ein
(4)
式中,T(x,y)是在口径Ω={(x,y)||x| 根据等效原理,将口径上的电场分布等效为磁流Jm[7-9,11] Jm=-z×EA (5) 式中:z是坐标系z方向单位矢量;等效电势A为 A=ε∬ΩJmG0dxdy (6) 其中:ε是口径的介电常数;G0是电磁波在自由空间传播时的格林函数,可表示为 (7) 工作区内任意点(xQ,yQ)的场分布可以表示为[22-23] (8) 式中:R是源点(x,y)和工作区场点(xQ,yQ)之间的距离矢量;k0是波数;积分区域为口径区域Ω。 工作区场的分布可通过式(8)获得。为了分析近场均匀性,提出了4个评价指标:Epv、Erms、φpv和φrms。Epv和φpv分别是在工作区内幅度和相对自由平面波的相位峰谷值[13,22-23],而Erms和φrms是在工作区内幅度和相对自由平面波的相位均方根值[13,22-23]。 按照电磁绕射理论,场分布可以视为透射波束复合器的直达波和来自于边缘的绕射波的干涉叠加。为了便于区分这两种波,可在时域和角频域进行分析[8,11]。由式(8)获得的工作区内空间某一点(xQ,yQ)的标量场记为E(f),是频率f的函数,时域内e(R)可通过式(9)进行逆傅里叶变换从频域变换到时域。 (9) 其中:c是光速;R是源点(x,y)和工作区场点(xQ,yQ)之间的距离标量。 按照平面波谱理论,工作区场可以视为经过波束复合器散射后不同入射方向子波的叠加,进而进一步将直达波和绕射波进行分离[7, 9]。平面波角谱G(kx,ky)可以表示为[7, 9] kyyQ)]dxQdyQ (10) 其中:kx=k0sinθDcosø;ky=k0sinθDsinφ。G可以看做是空间场分布E的傅里叶逆变换。θD是散射波的入射角,为了避免截断效应,在上述变换过程中采用了汉明窗[7-9,11]。 以文献[4,13]提出的微反射镜阵列型波束复合器为例,波束复合器外形为正方形,边长D取1 m,工作区半径r取150 mm,波束复合器距离工作区距离dQ取500 mm,工作频率取13 GHz,最大入射角θMAX为20°,θS从0°到360°可变。本文约束场均匀性指标值Epv和φpv应当分别小于1 dB和10°[7-9,11]。对于Erms和φrms也可以根据需要作为约束指标进行设计,后面场分析中也将给出这两个值,但不作为约束性指标。 图2给出了场的均匀性指标随h的变化情况。随着入射角θ的增加,场的均匀性明显变差。因此,最大入射角(θ=θMAX)条件下的场均匀性决定了波束复合器的性能。进一步可以发现Epv和Erms先下降后上升,相位分布φpv和φrms也存在类似的趋势,为此h存在最优值使得各指标最小。在h=125 mm且最大入射角条件下,Epv和φpv最小值分别为0.91 dB和5.43°。 按照上述方法,由于对称性,这里仅给出中心区右边的θE的允许范围,如图3所示。在位置(y=375 mm)处,θE的上下界分别是1°和89°,均为正值,表示该位置的三角形应当为钝角三角形,并且钝角至少大于91°。假设每个三角形的参数均相同,每个三角形的最大宽度受到了θE最小值的限制。当y=0 m时,θE的上下界分别是24°和-24°,l可由htan(24°)=55.63 mm获得,一条边上的三角形数量n应当满足n>(D-2h)/55.63 mm=14。 图2 场均匀性指标随h的变化Fig.2 The field uniformity varies with h 图3 中心区右边(x=0.375 m)的θE的允许范围Fig.3 Allowable range of θE on the right edge (x=0.375 m) of the central region 为了验证上述设计方法,这里对比了3种边齿结构:锐角三角形、直角三角形和钝角三角形的场均匀性,如图4所示。其中,锐角三角形是等腰三角形,每一个钝角三角形包含两个角γ1和γ2,定义如图4(c)所示。 (a) 锐角 (b) 直角 (c) 钝角图4 边齿结构Fig.4 Serrated edges structure 其中,γ1设计为10°,满足αMIN>βMAX的约束条件。γ2随着n的增大而增加,但仍要满足αMIN>βMAX的约束条件。因此,γ2可以表示为γ1的函数,即 (11) 计算了不同入射角情况下,n从4到50时场均匀性随n变化的情况,如图5所示。对于钝角三角形边齿,Epv、Erms、φpv和φrms首先快速下降,直到n达到14后趋于平坦;当n超过28时,场均匀性能够满足要求。对于直角三角形边齿,场均匀性有着类似的趋势,但是波动比钝角三角形边齿要大。对于锐角三角形边齿,其场均匀性比较差,主要原因是锐角三角形不满足αMIN>βMAX的约束条件。当n等于28,按照式(10),γ2等于15.8°,最后设计钝角三角形参数是h=125 mm、n=28、γ1=10°、γ2=15.8°。 (a) θ=0° (b) θ=10° (c) θ=20° 表1给出了在θS=0°的情况下,θ分别为 0°、10°和20°时,场均匀性指标在边齿处理前后的对比分析结果。与之前分析一致,Epv、Erms、φpv和φrms最差值发生在θ=20°时,此时,Epv、Erms、φpv和φrms的最大值从2.87 dB、0.48 dB、18.76°和3.37°分别下降到1.00 dB、0.18 dB、8.41°和1.28°。分析结果表明,边齿能够有效压制边缘绕射波,且能够满足所需指标要求。 图6和图7是在入射角θ=0°和θ=20°(θS=0°)条件下,进行边齿处理前后工作区场的空间分布,包括幅度和相位分布。在边齿处理后,干涉形成的波包数量明显减少,意味着直达波和绕射波的干涉效应减弱。 表1 边齿处理前后的场均匀性对比Tab.1 Field uniformity comparison before and after serrating edges at φ=0° 图6 边齿处理前后的幅度和相位分布(θ=0°和θS=0°)Fig.6 The amplitude and phase distribution before and after serrating edges(at θ=0°and θS=0°) 图7 边齿处理前后的幅度和相位分布(θ= 20°和θS=0°)Fig.7 The amplitude and phase distribution before and after serrating edges(at θ=20°and θS=0°) 为了将直达波和绕射波分开,计算了场点(x=0,y=0)处1~20 GHz的空间场分布。频域采样点选为100。由式(9)计算出在入射角θ=0°和θ=20°条件下(当θS=0°时)的边缘处理前后的时域谱,如图8所示。为了便于比较,所有曲线进行了归一化处理。按照文献[11],当所要求的Epv小于1 dB时,单个边缘绕射波应当小于-25 dB。当入射波沿着z轴传播时,根据式(9),直达波的R值恰好是工作区中心到波束复合器中心的距离dQ的值(500 mm)。然而,当入射波以20°角入射时,因为相位中心随着入射角而变化,直达波R值为470 mm。 如图8所示,在未进行边缘处理的情况下,在直达波后有很多绕射波。当入射角是0°时,如图8(a)所示,来自于边缘的绕射波的R=703.15 mm,强度达-17.98 dB。在R=873.04 mm处,来自于各角的绕射波较弱,强度为-58.20 dB。当入射角是20°时,来自于边缘的绕射波发生了分裂,如图8(b)所示,分别位于R=539.06 mm和R=667.97 mm处,由于对称性被打破,强度分别是-22.86 dB和-23.45 dB。来自于角落处的绕射波强度有所增强,达到了-32 dB,并且位置发生了变化,移动到了R=878.91 mm处。进行边缘处理后,来自于边缘和角的绕射波被分散为多个更弱的绕射波[7]。当入射角是0°时,最大绕射波位于R=626.95 mm处,强度达-32.76 dB;当入射角是20°时,绕射波强度小于-35 dB,意味着绕射波被强烈地压制了。 (a) θ=0° (b) θ= 20°图8 不同入射角情况下边缘处理前后的时域场分布(θS=0°)Fig.8 The field distribution in time domain before and after serrating edges at different θ(θS=0°) 在角频域方面,来自边缘的绕射波可以被更清晰地分开,如图9所示。随着入射角的改变,直达波的角位置不变,而绕射波的位置几乎不变。因为波束复合器口径尺寸是0.5m,与dQ相等,因此绕射波来自于45°方向,如图9(a)所示。当入射角是0°时,来自边缘的绕射波位于45°方向,幅度达-31.44 dB。当入射角是20°时,如图9(b)所示,边缘相对入射波方向已不再对称,由于直达波恰好位于20°方向,因此来自于±45°方向的绕射波也将不再对称[11]。进行边缘处理后,绕射波被强烈地分散了,强度均小于-35 dB。 (a) θ=0° (b) θ= 20°图9 不同入射角情况下边缘处理前后的角域场分布(θS=0°)Fig.9 The field distribution in angular domain before and after serrating edges at θS=0° 为了改善波束复合器场的均匀性,本文提出了边齿设计方法,利用几何绕射和口径场积分理论设计边齿的参数,包括数量、高度及相关角度。首先,利用等效梯形场幅度切削设计边齿高度,根据Keller衍射定律设计边齿的角度,通过场均匀性分析找到最优的边齿形状及数量。然后,为了在场分析中区分直达波和绕射波,将空间场和频域场分别变换到角频域和时域。最后,分析比较边齿处理前后场的分布情况,通过示例发现,Epv、Erms、φpv和φrms的最差值发生在θ=20°时,此时Epv、Erms、φpv和φrms的最大值从2.87 dB、0.48 dB、18.76°和3.37°分别下降到1.00 dB、0.18 dB、8.41°和1.28°。结果表明,场的均匀性获得明显改善,且能够满足所提出的Epv和φpv分别小于 1 dB 和 10°的指标要求。
3 边齿设计与场分析示例
3.1 边齿设计示例
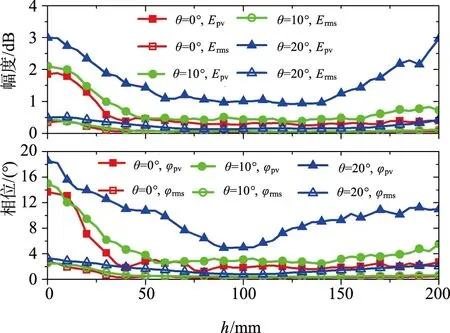
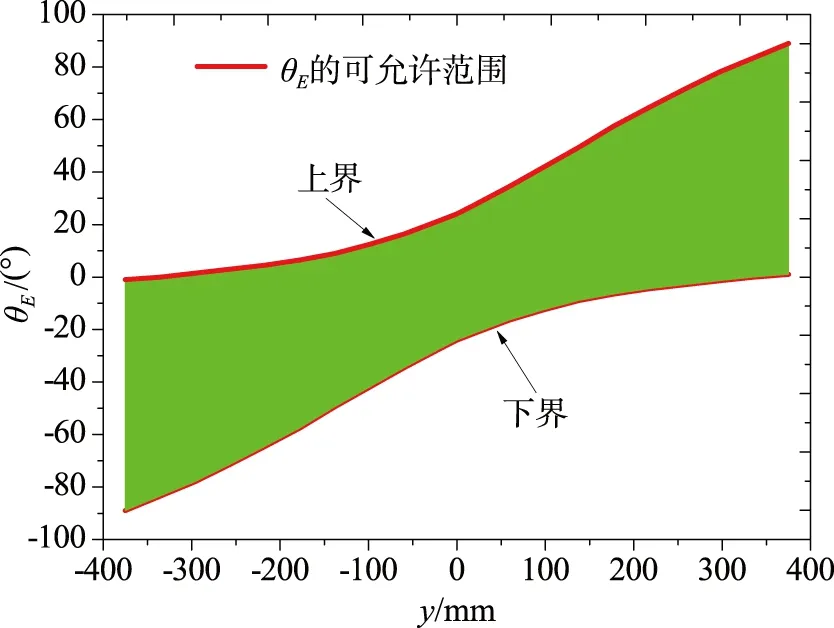
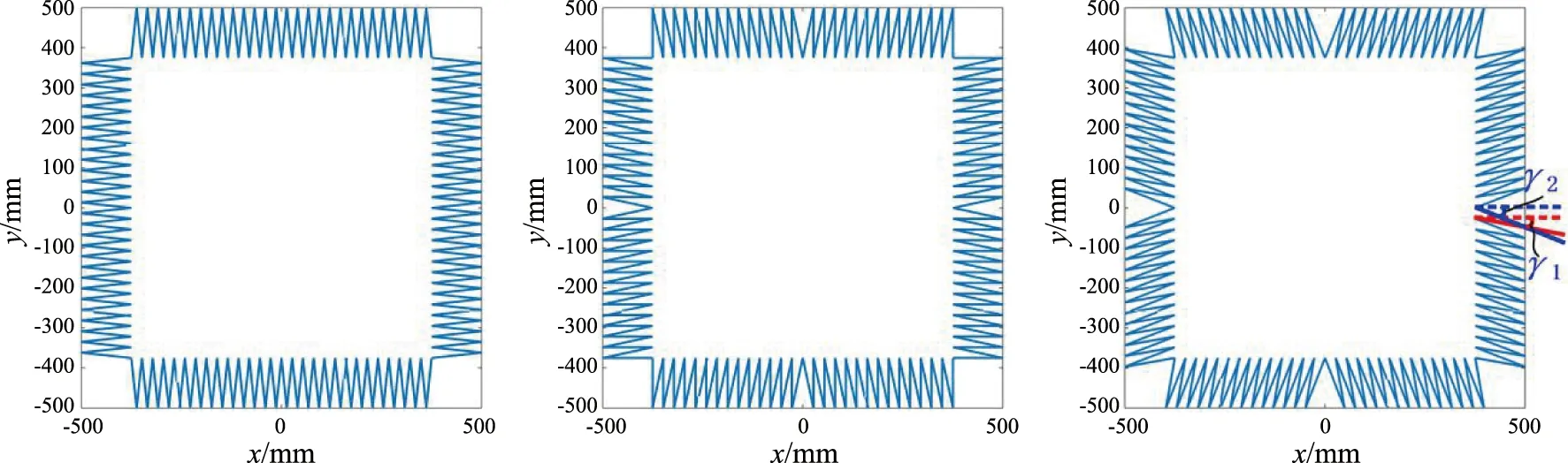



3.2 空域、时域、角域场分析





4 结束语

