基于多源数据可信度的制导精度融合评估
陈 璇 ,李 奇 ,李博文 ,肖意可,晏 良
(1. 国防科技大学 文理学院, 湖南 长沙 410073;2. 上海机电工程研究所, 上海 201109)
0 引 言
当前,随着科技的不断进步与发展,目标干扰样式和手段、导引头制导方式、作战场景与作战方式等日趋灵活多样。在复杂多变的电磁环境下,导引头能否准确命中目标,能否对其命中精度、命中概率、抗干扰能力等精度性能指标进行有效评估,是导弹武器系统试验鉴定中的一项重要研究内容。
目前,武器系统精度评估较为常用的方法主要有三类[1-8]:一是小子样快速收敛统计方法,适用于现场数据量不大,又无法获得其他可用信息的情况,包括序贯决策、Bootstrap抽样、Bayesian Bootstrap方法、随机加权法等;二是多状态信息融合统计方法,适用于现场试验数据量不大,但存在相关历史信息的情况,主要包括Bayes统计、Fiducial统计、百分统计学、模糊判决、D-S推理等;三是原型(仿真)系统试验统计方法,适用于由于安全、成本、规模等各种因素难以开展实装试验的情况,主要利用系统建模与仿真技术、模型的校验、验证和确认(verification,validation and accreditaion, VV&A)技术,确认原型系统或仿真模型,并通过少量外场试验,应用小子样方法,评估武器系统的性能。此外,还可以应用马尔科夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)方法,在试验分布参数确定、序贯信息融合方面应用前景广阔,可以避免大量的积分计算[3]。
1 多源数据制导精度评估原理与方法
对于制导精度评估问题而言,由于其性能试验类型具有多源性,覆盖面十分广泛,既包括系统级外场原型试验,也包括数值模拟试验、半实物仿真试验、挂飞试验、地面静态模拟试验等替代等效试验。受地域、成本、资源等因素的限制,系统级外场原型试验状态下的试验数据较少,具有小子样的特点,单纯靠少量的原型试验数据难以有效评估制导精度。这时,进一步扩充信息源,充分利用其他类型的替代等效试验数据作为先验信息,在此基础上开展融合评估,是较为常见的一种解决思路,属于多状态信息融合统计方法。
在评估过程中需要注意的是,替代等效试验与系统级外场原型试验是在不同状态下进行的试验,因此,两类试验结果并不属于同一总体,不能直接进行融合。工程中常用的方法是从物理机理模型出发,将替代等效试验结果通过折合或者误差补偿,推算到原型试验状态下,再与原型试验小样本数据融合评估。然而,在推算过程中,受各种误差因素的影响,折合或者误差补偿时必然会产生一定的折合误差。此外,当替代等效试验折合后的数据与原型试验小样本数据存在显著差异时,融合结果也会出现较大的偏差,这时需要从数据分布差异的角度考虑,利用数据相容性检验结果判断两种类型的试验数据是否能够进行融合,并根据得到的数据可信度加权融合。然而,在替代等效试验数据有具体物理机理来源信息的情况下,仍只从数据层面去度量可信度,则评估结论会显得过于片面[1-3]。
因此,本文提出了一种引入复合可信度的多源数据制导精度评估方法,从数据分析和物理机理两个角度进行有机结合,通过数据相容性检验和物理机理折合误差结果,计算了替代等效试验折合样本数据对应的复合可信度。在此基础上,以服从正态分布的制导精度指标脱靶量为例,利用Bayes方法对多源数据进行融合评估,具体流程如图1所示。
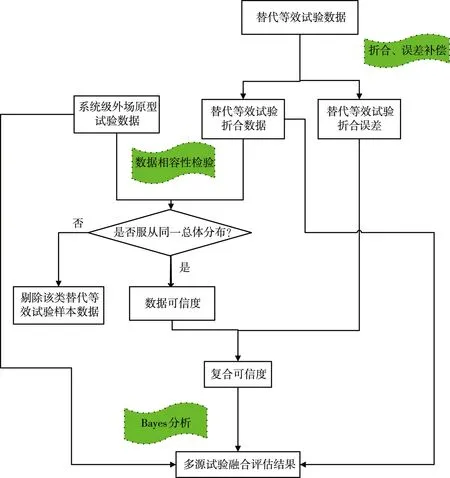
图1 多源数据制导精度融合评估流程图Fig.1 Flow chart of the guidance precision fusion evaluation on multi-source data
2 基于数据相容性与物理机理折合误差的先验信息复合可信度计算
2.1 数据相容性检验及对应先验信息可信度计算[3]
从数据分析角度而言,先验信息可信度计算方法一般是基于数据的相容性检验。目前较为常用的方法是运用秩和检验法对两类数据进行相容性检验。针对制导精度而言,需要用系统级外场原型试验数据样本与不同类型的替代等效试验折合后的数据样本进行检验。若检验后两者分布差异较大,不能看作同一总体,则该类替代等效试验折合样本应予以剔除,不能与系统级外场原型试验数据样本放到一起进行融合。
记X=(X1,…,Xn1)为系统级外场原型试验样本,Y=(Y1,…,Yn2)为一种类型的替代等效试验折合后数据样本(先验子样),要求验证X与Y是否属于同一总体,为此,引入竞择假设
H0:X与Y属于同一总体↔H1:X与Y不属于同一总体
运用秩和检验,将X、Y混合,由小到大排序,得次序统计量Z1≤Z2≤…≤Zn1+n2。
记Yk=Zj,即Y中的第k个元Yk在混合排序中的名次为j,称它为Yk的秩,记作γk(Y)=j。
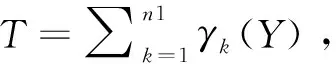
于是在获得子样X、Y之后,计算秩和T,在检验水平α之下,若T1 先验子样Y的可信度p可定义为当采纳H0事件时H0成立的概率,即X和Y属于同一总体的概率,则有p=P{H0|A}。 利用Bayes公式推导可得 (1) 式中:β为采伪概率;P(H0)为先验概率。 下面分别讨论采伪概率β和先验概率P(H0)的计算方法。 确定检验水平α之下的临界区域为D={T≤T1或T≥T2},根据采伪概率定义,有β=P{T1 采伪概率β的计算相对较为复杂,想给出其解析表达式相对困难,通常采用Bootstrap方法估计分布,并通过Monte Carlo仿真进行计算。针对制导精度指标,如脱靶量,一般认为X、Y均服从正态分布,于是相容性检验问题可转化为正态总体下均值与方差的相等性检验问题。 H0:D1/D0=1↔H1:D1/D0=λ2>1 计算步骤如下: Step1选择检验的显著性水平α; Step2查找自由度为(n1-1,n2-1)的Fα/2和自由度为(n2-1,n1-1)的Fα/2; 此时,采伪概率β=P{F1-α/2 β=P{F1-α/2 P{F1-α/2/λ (2) 因此,可得F1-β=Fα/λ,通过查找F分布表,可以得出采伪概率β。 在式(1)中,当无任何其他先验信息可利用时,可取P(H0)=1/2,此时可信度p简化为 同理,完全加权负项集NI(Negative Itemset)关联度(all-weighted Negative Itemset Relevancy,awNIR)的计算如式(9)所示: (3) 针对制导精度试验,随着制导方式、目标特性、环境、干扰策略与样式等各个因素的变化,脱靶量、命中概率等精度指标也随之产生变化。不同类型的替代等效试验制导精度结果均可依据物理机理模型折合到系统级外场原型试验下,但是由于不同类型下各因素的试验环境和状态不一,以及折合过程中的误差传播、随机扰动等带来的影响,折合结果都会产生误差[9-13]。此时,将不同类型的替代等效试验折合数据作为先验信息,若能够测算到替代等效试验折合过程产生的误差和观测总误差,则对应的先验概率P(H0)可以根据替代等效试验的折合精度进行计算。 现设共有M类多源替代等效试验,每类试验的数据样本数记为Ni(i=1,…,M),分别折合到系统级外场原型试验状态下。记第i类替代等效试验数据折合样本的折合误差为σi,可以依据物理模型的精度和误差传播关系推导得到观测总误差σ总i,则第i类替代等效试验折合样本的先验概率P(H0)i可表示为 (4) 式中,参数ηi和γi为衡量变化速率的参数。对于不同类型试验应该选取不同值,一般取ηi∈[0.5,2],γi∈[1,2],此时函数变化速率相对较为缓慢,也可以结合工程经验对参数进行选取[14]。 可以看出,若σi=0,即表示折合的方法和过程未产生任何折合误差,这是一种理想情况,此时P(H0)i=1,代入式(1)后得先验信息复合可信度为1,即表示该类替代等效试验折合样本完全可信,可以直接与系统级外场原型试验样本进行融合。若σi≈σ总i,并取ηi=1,得P(H0)i≈1/2,说明该类替代等效试验折合样本中的观测误差基本都是由折合过程产生的,此时等价于无先验信息可利用的情况,直接利用数据相容性检验得到的可信度与系统级外场原型试验样本进行加权融合。 从物理机理角度而言,本节中先验概率P(H0)i的定义其实表征了第i类替代等效试验折合样本与原型试验样本的一种相似程度。观测总误差中折合误差越低,表示该类试验折合后的样本数据越可信,这与式(1)中先验信息可信度随先验概率增大而递增的变化规律也是一致的。 先验信息可信度的准确度量对Bayes融合估计结果影响很大。本节提出的先验概率计算建立在对误差机理和误差折合精度的分析基础上,对应算出的复合可信度具有一定的准确性。 给定先验样本X=(X1,X2,…,Xn),记参数θ的估值为δ(X),令L(θ,δ)为损失函数。此时在给定X之下的平均损失为 (5) 式中,π(θ|X)为θ的验后密度函数。 (6) 损失函数L(θ,δ)取平方误差损失函数L(θ,δ)=(θ-δ)2,则θ的Bayes估计即为其验后分布π(θ|X)的数学期望值δ(X),即 (7) 估计的后验方差为 MSE(δ(X)|X)=Eθ|X(θ-E[θ|X])2=Var(θ|X) (8) (9) (10) 假定无先验信息可用,则有无信息先验 π(μ,D)∝D-1,根据Bayes公式有 (11) 经计算,可以得到正态-逆Gamma分布超参数α0、β0的估计值为 (12) (13) 若不考虑替代等效试验的可信度,直接将样本X(1)与X(0)融合估计,则有(μ,D)服从正态-逆 Gamma 分布,记 (14) 分布密度函数为 (15) 可以推出,超参数α1、β1的估计值为 (16) (17) 将一类替代等效试验的推断结果拓展到M类替代等效试验下,可以得出,(μ,D)服从正态-逆Gamma分布,超参数αM,βM的估计值为 (18) 则可得到μ和D的Bayes估计为 (19) μ和D的后验方差为 (20) 在有先验信息时的Bayes融合估计中考虑M类替代等效试验折合样本的可信度。根据先验信息可信度的计算,可以得到第i类替代试验折合样本的可信度为pi,对试验结果进行加权融合,则可以得到(μ,D)服从正态-逆Gamma分布的超参数α′M,β′M的估计值为 (21) 此时,μ和D的Bayes估计为 (22) 后验方差为 (23) 以制导精度脱靶量指标为例进行仿真。脱靶量服从的总体分布其实是未知的,但是为了使仿真结果便于比较,这里假设其服从正态分布N(25,10),从中随机抽取样本数为6的系统级外场原型试验子样(单位为m),记为X(0)=[5.721 7, 30.214 1, 15.089 8, 22.468 7,35.092 7,25.510 1]。另外,设现有两类替代等效试验,假设其折合后的脱靶量结果分别服从正态分布N(25,11)和N(25,10.2),从中各随机抽取样本数为20和10的样本。可以看出,这里两类替代等效试验折合数据的分布与原型试验的分布均有一定差异,第一类替代等效试验样本量较大,但与原型试验总体分布对比,分布差异相对较大;第二类替代等效试验样本量相对较少,但其分布差异与原型试验总体分布较为接近。 表1给出了三种脱靶量评估方法的结果,分别给出了均值、方差的点估计以及两个估计的后验方差。第一种方法未融合替代等效试验的折合样本,直接利用系统级外场原型试验样本进行估计;第二种方法经相容性检验判定两类替代等效试验折合样本均与原型试验子样属于同一分布后,未考虑物理机理影响,仅用数据相容性检验得到的可信度,利用Bayes方法融合估计,先验概率取P(H0)=1/2;第三种方法基于复合可信度进行Bayes融合评估,两类替代等效试验折合样本的折合误差分别取σ1=3.5,σ总1=4,σ2=1,σ总2=10,并均取η1=η2=γ1=γ2=1,代入式(4)可得,两类替代等效试验折合样本的先验概率分别为P(H0)1=0.533 3,P(H0)2=0.909 1。取α=0.025,利用F检验计算得出两类替代等效试验的采伪概率β1=0.035 5,β2=0.026 5,代入式(1)可得,两类试验的信息可信度分别为p1=0.969 0,p2=0.997 3。 表1 三种脱靶量评估方法对比Tab.1 Comparison of three miss distance assessment methods 对比三种方法的评估结果并进行分析,可知: 1) 方法1估计结果与仿真的初始分布N(25,10)差异极大,且均值与方差估计的后验方差都相对较高。这主要是因为系统级外场原型试验数据样本量较少,估计结果与采样数据高度相关。 2) 方法2与方法3均利用替代等效试验折合样本扩充了信息源,虽然两类替代等效试验与原型试验分布有一定差异,但是融合后的评估结果与方法1相比更接近于仿真的初始分布,且均值、方差估计的后验方差均大幅降低。 3) 本例中第一类替代等效试验样本量较多,但折合精度不高;第二类样本量相对较少,但折合精度更高。引入复合可信度的多源数据Bayes融合评估方法(即方法3)的计算结果与方法2的计算结果相比,均值与方差估计相对更为稳健,后验方差也有所降低,且有效降低了低可信度先验信息的影响,结果更为合理。 本文主要针对多源数据制导精度的融合评估问题,以服从正态分布的脱靶量指标为例,提出了一种依托数据相容性检验和物理机理折合误差来计算多源替代等效试验信息可信度的方法,并以此为基础,利用Bayes方法与系统级外场原型试验样本加权融合评估。仿真结果表明,引入复合可信度后的Bayes融合评估方法能够从一定程度上改善单纯依靠外场原型试验小子样评估结果不准确的情况,使精度指标的评估结果更为精确、稳健,具有实用性。 本文提出的这种思路其实可以看作是工程化折合方法与数理统计方法的有机结合,与物理工程背景结合紧密,具有合理性和实用性。文中制导精度指标以脱靶量为例,若对命中概率、抗干扰概率等概率型指标开展评估,替代等效试验信息可信度的计算方法仍然适用,而在Bayes融合评估中则需要采用二项分布参数的相关估计方法[16-17]。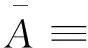
2.2 采伪概率β计算方法
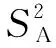
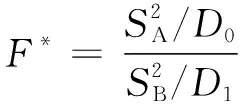
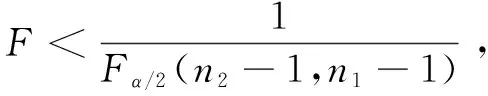
2.3 先验概率P(H0)计算方法
3 基于复合可信度的Bayes融合评估
3.1 经典Bayes估计[3,14-15]
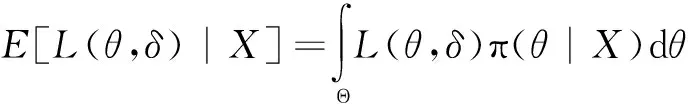
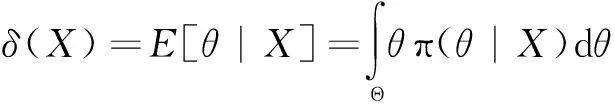
3.2 无先验信息时的分布参数确定[14]
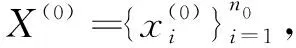
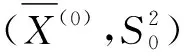
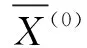
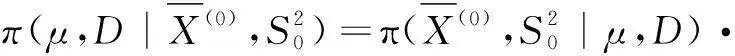
3.3 有先验信息时的Bayes融合估计
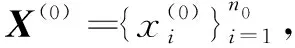
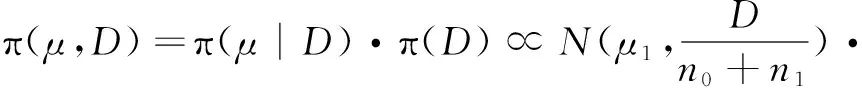
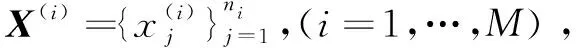
3.4 基于复合可信度的Bayes融合估计
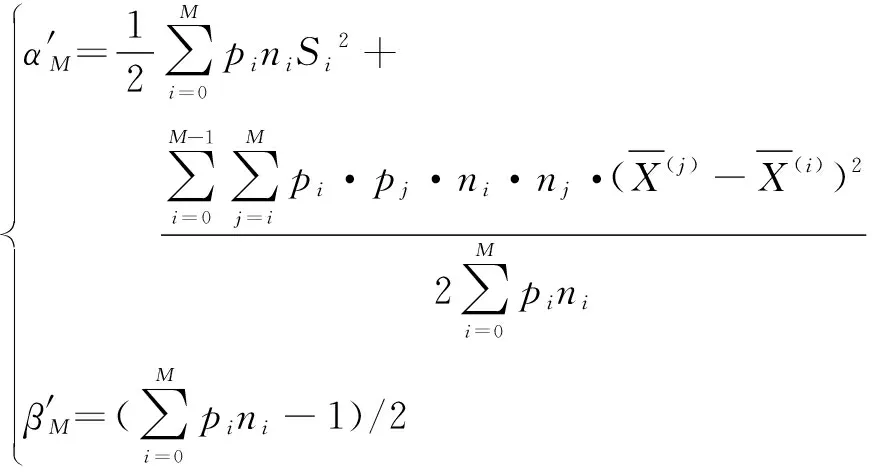
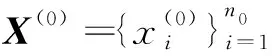
4 仿真案例

5 结束语

