结构与参数对曲轴扭振减振器减振效果影响研究

刘佳鑫，顾灿松，，袁兆成，杨征睿

（1.吉林大学汽车工程学院，吉林 长春 130022；2.中国汽车技术研究中心汽车工程研究院，天津300162）

1 引言

汽车发动机曲轴系的扭振固有频率较低，在工作转速范围内，常有扭转共振的现象发生。曲轴系的扭振水平也是发动机NVH 性能的基本指标之一。为降低曲轴系扭振的危害，一般在曲轴前端加装减振皮带轮，又称作曲轴扭振减振器（TVD），汽油机中为节省安装空间和制造成本，多采用的单级橡胶减振器，如图1 所示。目前橡胶减振器主要有两种结构形式：一种为减振器惯量环ring 上带有楔形环槽，直接加载前端轮系皮带，在文中称为承载式减振器，如图1（a）所示。这样的结构目前在汽油机中应用最为广泛；另一种则是以与曲轴刚连的减振器轮毂HUB 加载前端轮系皮带，而惯量环ring 为自由端，这种结构在文中称为非承载式减振器，如图1（b）所示。

图1 减振皮带轮剖面图Fig.1 Sectional View of Bearing TVD and Non-Bearing TVD

橡胶扭振减振器的设计思想基于动力吸振器原理[1]，应用较为广泛的设计方式主要有两种：一种令曲轴主系统与减振器系统的扭振固有频率相等，利用共振时两者振动频率相等方向相反降低共振振幅，此种设计方式称作共振式设计[2]，主要用于消减曲轴某段转速范围内的扭转共振；另一种文中称作最佳参数设计（常用经验公式确定参数），是在共振式思想的基础上进行部分参数优化，使其减振效果尽可能覆盖发动机整个工作转速范围。国外对于橡胶式减振器的减振理论及动态特性的研究较为完善，相关计算模型有Maxwell模型、Voigt 模型、Kelvin-Voigt 模型等[3-5]。国内学者近年来在这一领域的研究也在跟进，研究成果涵盖曲轴系扭振集总参数模型、分数导数动力学模型和Kelvin-Voigt 模型的理论计算，减振器当量参数设计和橡胶环参数匹配及优化等方面[6-8]。

根据经典的减振器分析理论[9]，惯量环作为曲轴主系统的吸振结构，其上不应有外力矩作用，即减振器理论上应为非承载式结构，但相比于承载式，非承载式减振器在发动机上的应用较少。关于这两种结构减振器的减振效果差别，并未有明确的定论和具体的计算探究，更多的认知则来自相关工程实践经验，非承载式结构略好，但究竟是非承载式减振器无论采用何种设计时减振效果都要好于承载式，还是只在某些特定情况下才好于承载式，也没有普遍适用的结论。因此采用理论计算、多体动力学仿真及实验验证相结合的方式对减振器采用两种结构形式及设计参数时其减振效果的差别进行深入的研究。

2 减振器减振效果的理论计算

2.1 扭振计算模型的构建及求解

首先针对曲轴系扭振系统进行一般性问题的理论计算，应用集总参数思想构建并简化曲轴系扭振计算模型，完全保留扭振减振器的结构，如图2 所示。曲轴主系统（包括飞轮、曲轴和减振器轮毂Hub）由当量扭转刚度c1和当量转动惯量I1组成，上面作用着缸压激励力矩减振器系统（橡胶环与惯量环Ring）由c2，I2组成，I1和I2之间作用有橡胶环的阻尼系数ζ。前端轮系负载在非承载式减振器中作用在轮毂HUB 上（惯量盘I1）；在承载式减振器中作用在惯量环Ring（惯量盘I2）上。计算中假设前端轮系载荷为正弦载荷以模拟发动机前端附件波动的负载力矩。

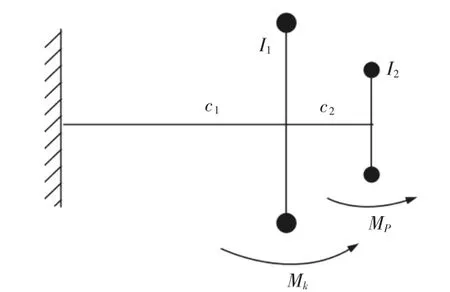
图2 曲轴系扭振系统简化模型Fig.2 Simplified Model of Crankshaft Torsional Vibration System

由达朗伯原理及多自由度系统振动方程[9]，有非承载式和承载式减振器I1和I2的运动微分方程：

非承载式：

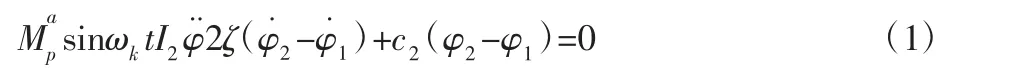
承载式：

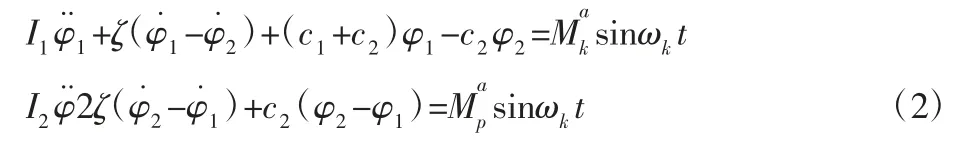
设解的形式为：

将解（3）代入式（1）和式（2）并令sinωkt 和cosωkt 项系数对应相等，分别求得式（1）和式（2）的线性方程组如下：

其中，v=ω2/ω1（定调比）；f=ωk/ω1（强迫振动频率比）（质量比）；D=ζ/2I2ω2）（阻尼比）（扭转静变形）；（振幅放大系数）；R0=Φ20/Φ10；

工程上对于发动机曲轴系扭振的测量多以减振器轮毂Hub的扭转位移角度为参考，因此计算主要关注振幅放大系数R1，求得非承载式和承载式减振器Hub 端振幅放大系数R1和表达式如下，可以看出振幅放大系数是关于f、μ、v、D、R0的函数。

2.2 共振式设计时非承载式与承载式减振器对比

共振式设计时，曲轴主系统的扭振固有频率ω1与减振器系统扭振固有频率相等。由于阻尼的存在，减振器系统的扭振固有频率是其无阻尼时固有频率ω2的倍，有：

因此当采用共振式设计时，有ω1=ωd，即定调比阻尼比D 的范围通常在（0～1）之间[9]。同时由之前代换不难得出R0计算中激励载荷和前端轮系负载均为定值，文中取R0μv2=0.2 为定值。

以质量比μ=0.05 为例，当D=0、0.1、0.2、0.3 时，有定调比v=1、1.00504、1.02062、1.04829，此时由式（6）、式（7）计算得到的共振式非承载与承载减振器Hub 端振幅放大系数曲线，如图3 所示。

从图中可以看出，D=0 时为无阻尼情况，共振式非承载减振器能将共振点（f=1）处振幅衰减至零，而承载式则不能，同时两种结构减振器在共振点两侧都会产生两个新的振幅峰值点，随着阻尼比的增加，后面的振幅峰值逐渐消失；在第一个振幅峰值点附近，共振式非承载减振器Hub 端振幅明显小于承载式减振器，减振效果要更好；当频率比较大时，两种结构减振效果相差不大。发动机曲轴系扭振固有频率一般在（200～350）Hz 左右，以四缸机为例，其转速2 阶谐量对曲轴系扭振影响最大，假设其固有频率为200Hz，转速2 阶谐量发生共振时曲轴需达6000r/min，因此对于曲轴系扭振的研究与控制，重点针对共振点附近及前一个振幅峰值点。而计算结果说明，采用共振式设计时，明显非承载式减振器的减振效果更好。

图3 μ=0.05 时共振式减振器幅频特性曲线Fig.3 The Frequency-Response Curves of Resonance TVD When μ=0.05

2.3 最佳参数设计时非承载与承载式减振器对比

根据图3 可知两种结构减振器的四条曲线均通过两个固定点，即两点的位置与D 无关。最佳参数设计就是通过调节定调比ν 令两固定点的纵坐标相等，调节阻尼比D 令两点为振幅放大系数峰值点，如此一来可使较高的振幅峰值点处振幅降低，并使振幅在整个转速范围内保持一个较低的状态，两个参数分别称为最佳定调比和最佳阻尼比。

常用经验公式的推导以非承载式减振器为例，由式（6）有：

令k1/k2=k3/k4，则R1的结果和D 无关，有：

若令D=∞，由式（6）有：

令RⅠ=RⅡ，则

联立式（9）、式（11）求得最佳定调比：

对于最佳阻尼比DOPt，可采用极大值法：将式（12）代入式（6），并对公式进行适当的简化处理，求对f2的导数，使之分别在Ⅰ、Ⅱ两点处为零，解得vopt 下最佳阻尼比Dopt 的经验公式：

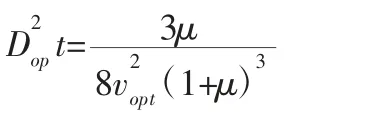
对于承载式减振器的最佳定调比vopt、最佳阻尼比DOPt 计算流程完全相同，具体公式不再进行推导。同样以μ=0.05 为例，R0μv2=0.2 为定值，非承载式减振器的最佳设计参数为：

承载式减振器的最佳设计参数为：

采用以上最佳设计参数时非承载式与承载式减振器的幅频特性曲线以及两种结构减振器采用各自最佳阻尼比DOPt 下的共振式设计时的幅频特性曲线对比，如图4 所示。根据计算结果，质量比μ、阻尼比D、激励力矩和负载力矩都相等时，减振器采用最佳参数设计相比于共振式设计可将频率比小于1 时的扭振振幅峰值大幅降低，减小曲轴系扭振的危害，频率比大于1 时，共振式设计的减振效果更好；采用共振式设计时，非承载式减振器的减振效果明显好于承载式结构，但减振器采用最佳参数设计时，两种结构形式减振器的减振效果差别甚小，都能很好地降低曲轴系的扭振。

图4 不同设计参数时非承载与承载减振器频响曲线对比Fig.4 Frequency-Response Curves of Non-Bearing TVD and Bearing TVD Designed in Different Methods

3 多体动力学建模及实验验证

以上计算初步可知共振式设计和最佳参数设计在减振效果上各有优势，而且非承载式结构也并非任何情况下都好于承载式结构。下面针对研究问题基于某款缸内直喷三缸机建立多体动力学仿真模型，继续进一步的研究。

3.1 虚拟样机模型的建立

目前对于复杂大型机械结构的数值仿真计算广泛应用多体动力学方法[10]，为实现对该发动机曲轴系扭振精确求解，仿真模型采用柔性体多体动力学方法建模，考虑结构件弹性对计算结果的影响，将曲轴系和发动机机体视为柔性体，进行有限元网格划分并进行模态缩减，活塞连杆视为刚体，连杆大头轴承、发动机悬置和曲轴止推轴承简化为弹簧阻尼单元，曲轴主轴承采用弹性液力润滑轴承模型，缸内爆发压力通过实验测得，前端附件轮系采用多体动力学结构化方法建模，相关参数边界全部采用实测值，由此建立该机曲轴系及前端轮系的多体系统仿真模型，如图5 所示。为实现将前端轮系载荷加载到曲轴系扭振模型中，将两模型分别通过减振器缩减后代表轮毂Hub 和惯量环Ring 的节点进行耦合，完成非承载式及承载式结构的曲轴系-前端轮系多体系统联合仿真模型。

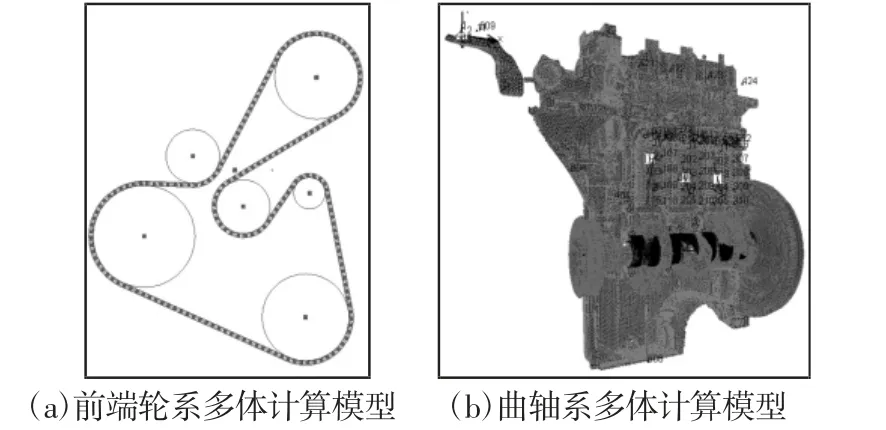
图5 多体动力学计算模型Fig.5 Simulation Model of Multi-Body Dynamics

出于对计算时间及工作量的考虑，对于不同结构形式（前端载荷不同加载位置）对减振器减振效果的影响的计算采用该三维仿真模型，对于不同设计参数对减振器减振效果的影响计算采用由该三维模型离散得到的一维仿真模型。

3.2 曲轴模态实验与发动机扭振台架实验

为保证多体动力学计算结果的可信度，需进行曲轴模态实验和发动机扭振台架实验对仿真模型的计算精度进行验证。首先验证曲轴有限元模型的精度，对曲轴进行模态测试，实验时采用弹性悬挂，以单点激励多点响应的方法展开实验，测量每个测点的振动加速度信号，通过集总平均法得到模态频率，测点布置时尽量避开曲轴的模态节点。然后进行曲轴系扭振台架实验，以验证仿真模型扭振计算结果的准确度，实验时在减振器轮毂Hub上安装光电编码器，通过数采前端测量其扭转角度，传感器安装位置，如图6 所示。实验工况为（1000～6000）r/min 时节气门全开的加速工况。

图6 传感器安装示意图Fig.6 Installation Place of the Sensor

3.3 仿真模型计算精度验证

曲轴有限元模型计算的模态频率、曲轴一维结构化模型计算的模态频率和曲轴模态实验测得的模态频率的对比结果，如表1 所示。三维和一维模型的模态频率计算值与实验值相比，总体误差要远小于一般工程计算5%的要求，确保了计算模型能够准确模拟曲轴的实际工作状态。

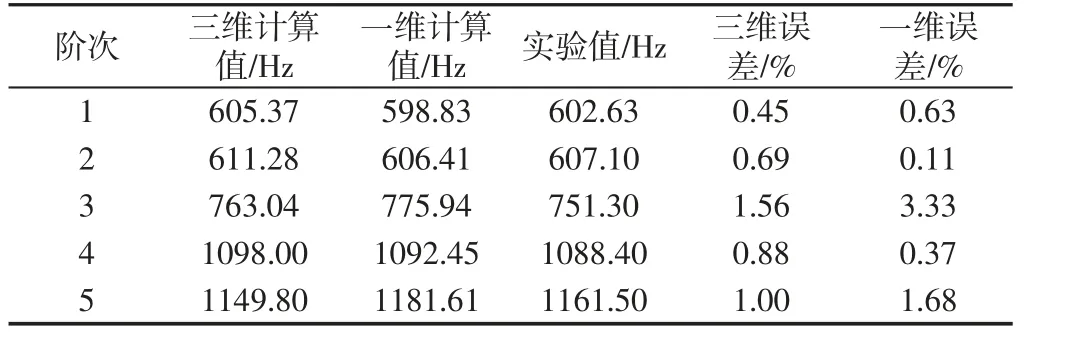
表1 曲轴模态频率计算值与实验值对比Tab.1 Modal Comparison of Simulation and Experiment

三维多体动力学模型计算得到的各主阶次减振器Hub 端扭振振幅计算结果，如图7（a）所示。台架实验测得的各主阶次减振器Hub 端的扭振振幅实验结果，如图7（b）所示。可以看出，扭振计算结果各阶次曲线的走势及振幅大小与实验结果保持了较高的一致性，建模精度较高。需要特别说明的是，图7（b）中1.5 阶次5300r/min 至5500r/min 范围内存在振幅峰值，经对实验台架的整体分析，得出此峰值是由于激励频率达到了传感器支架的固有频率而发生共振而引起，并非是曲轴扭转共振，属于测试误差范畴。

图7 仿真与实验Hub 端扭振阶次结果对比Fig.7 Comparison of Torsional Order Tracking Results of Simulation and Test

一维模型和三维模型计算得到的共振阶次上的共振振幅及临界转速与台架实验结果的对比，可以看出计算值与实验值吻合较好，三维和一维曲轴系扭振模型的计算精度都可以满足工程计算要求，应用验证过的仿真模型继续探究结构形式和设计参数对减振器的减振效果的影响，如表2 所示。

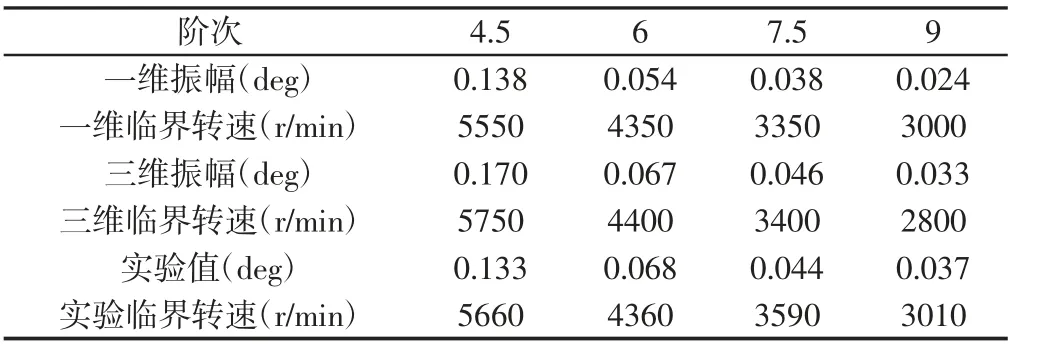
表2 减振器轮毂Hub 端扭振振幅计算值与实验值对比Tab.2 Comparison of Hub Torsional Amplitude Result Obtained by Dynamic Simulation and Experiment Test

4 减振器减振效果的多体动力学计算

4.1 设计参数对减振器减振效果的影响

该三缸机的曲轴扭振减振器，如图1（b）所示。采用非承载式结构形式，其对应橡胶环扭转刚度为c2=32000Nm/rad，橡胶环粘性阻尼系数ζ=1.6Nm.s/rad，阻尼比D=0.1034，惯量环ring 的转动惯量为0.00187kg.m2；减振器扭振固有频率为ωd=655Hz，曲轴主系统扭振一阶固有频率经计算为ω1=547.2Hz。应用简化后的一维曲轴系扭振计算模型，调节相关设计参数，对比该减振器在采用原设计方式、共振式设计以及最佳参数设计时的减振效果。采用共振式设计时，调节橡胶环扭转刚度，视材料阻尼系数为定值，使减振器与曲轴主系统的扭振固有频率相等，有：

采用最佳参数设计时，有：

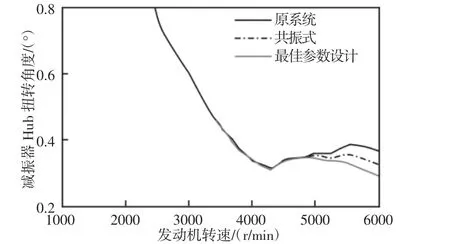
图8 不同设计参数时轮毂Hub 端扭振振幅对比Fig.8 Comparison of Hub Torsional Amplitude with Different Design Parameters

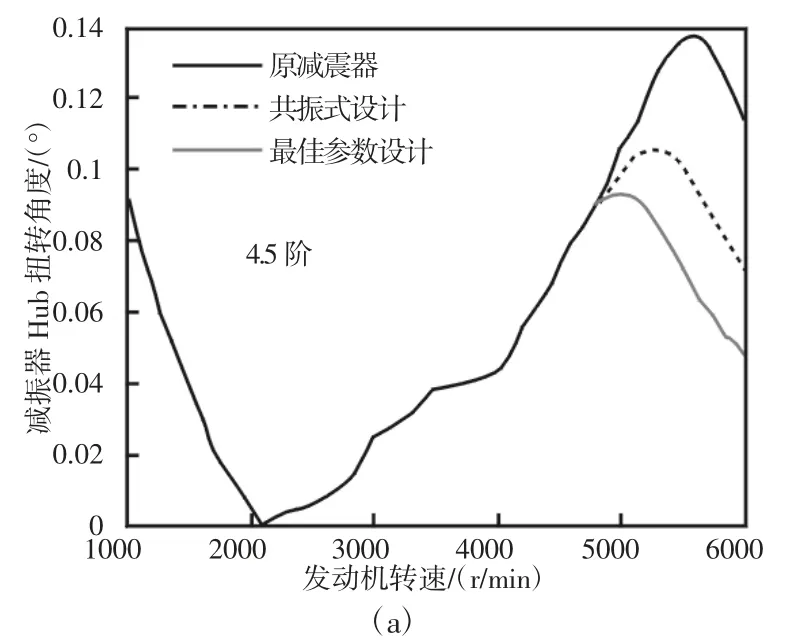
图9 共振阶次Hub 端共振振幅对比Fig.9 Comparison of Hub Torsional Amplitude at Resonance Orders

减振器轮毂Hub 端在采用三种设计参数时的扭振振幅总级随转速变化的对比，如图8 所示。在共振阶次4.5 阶、6 阶、7.5 阶、9 阶上的共振振幅对比情况，如图9 所示（1.5 阶和3 阶该转速范围内未发生扭转共振）。

可以看出，将原减振器的设计参数调整为共振式设计或采用最佳参数设计时，无论是扭振振幅总级还是各主阶次下共振振幅均有明显降低；当减振器采用最佳参数设计时，计算转速范围内的整体减振效果相比于共振式设计更好，与前文中计算结果相吻合。同时由计算发现，通过继续调小橡胶环的刚度，可使高转速下的轮毂Hub 端扭振振幅略微降低，但由此引发髙阶次下的第二个振幅峰值急剧增大，而且橡胶刚度越低，其耐疲劳性越差。因此，在发动机常用工作转速范围内，扭振减振器对曲轴系扭振的综合减振效果以最佳参数设计时最好。

4.2 共振式设计时两种结构形式减振效果对比

应用曲轴系-前端轮系三维仿真模型计算采用共振式设计时两种结构形式减振器的减振效果。承载式和非承载式结构在计算模型中的体现即为前端轮系载荷加载位置的不同：非承载式计算模型中前端轮系载荷加载在减振器轮毂Hub 节点上；承载式计算模型中载荷加载在惯量环ring 上。通过调节橡胶环有限元模型的材料属性中的弹性模量和阻尼系数使减振器达到共振式设计，计算工况为（1000～6000）r/min 转速范围内转速间隔为200r/min 的稳态转速，每个工况计算25 个工作循环。

图10 扭转振幅总级对比Fig.10 Comparison of Hub Torsional Amplitude of Non-Bearing TVD Hub and Bearing TVD Hub

图11 共振阶次振幅对比Fig.11 Comparison of Resonance Amplitude at Resonance Orders

减振器采用共振式设计时非承载式和承载式减振器轮毂Hub 端的扭振振幅总级随转速变化的对比，如图10 所示。共振阶次4.5 阶、6 阶、7.5 阶和9 阶上两种结构减振器共振振幅的对比情况。

可以看出，采用共振式设计时，无论是Hub 端扭振振幅总级还是共振阶次上的共振振幅，非承载式减振器均远小于承载式，非承载式减振器的减振效果更好，如图11 所示。

4.3 最佳参数设计时两种结构形式减振效果对比

采用最佳参数设计时非承载式与承载式减振器的对比，同样采用前文中计算模型与计算工况，调节橡胶环有限元模型的材料属性使减振器达到最佳参数设计方式。减振器采用最佳参数设计时非承载式轮毂Hub 和承载式轮毂Hub、惯量环Ring 的扭振振幅总级随转速变化的对比，如图12 所示。

图12 扭转振幅总级对比Fig.12 Comparison of Torsional Amplitude of Non-Bearing TVD Hub，Bearing TVD Hub and Bearing TVD Ring

共振阶次4.5 阶、6 阶、7.5 阶和9 阶上非承载式轮毂Hub 与承载式Hub 和ring 上的共振振幅的对比，如图13 所示。

可以看出：在整个计算转速范围内，采用最佳参数设计时两种结构形式减振器Hub 端扭振振幅总级相差不大，减振效果非常接近；但在各个共振阶次上，非承载式减振器对共振时Hub 端振幅峰值的衰减作用略好于承载式减振器，减小了曲轴系扭振共振带来的危害；减振皮带轮的另一重要作用是降低曲轴传递到前端轮系的转速波动以改善前端轮系工作状况，根据计算结果，非承载式减振器的Hub 端扭振振幅总级以及共振阶次的共振振幅均远小于承载式减振器的惯量环ring，即应用非承载式减振器时前端轮系的转速输入更加稳定，工作状况更好。

图13 共振阶次振幅对比Fig.13 Comparison of Resonance Amplitude at Resonance Orders

5 结论

应用理论计算与结合有限元方法的多体动力学仿真研究了结构形式及设计参数对曲轴扭振减振器减振效果的影响，并得出以下结论：

（1）多体动力学计算结果与理论计算结果基本一致，当减振器采用共振式设计时，非承载式结构的减振效果要好于承载式结构；当减振器采用最佳参数设计时，两种结构的减振效果相差不大，但非承载式共振阶次上的共振振幅略小于承载式结构。综合而言，非承载式结构减振效果较好，且能更好改善前端轮系工作状况。

（2）当减振器结构形式相同时，常用的共振式设计和最佳参数设计两种方式的减振效果各有利弊，共振式设计较适合降低曲轴某段转速内的扭振振幅，而在发动机常用工作转速范围内，最佳参数设计时综合减振效果更好，但此时高阶次下第二个振幅峰值增大明显。

（3）建立了前端轮系-曲轴系扭振联合仿真模型，并对模型进行实验验证。结果显示，有限元模型和仿真模型均保持了较高的计算精度，能够很好的模拟曲轴的实际工作状态。文中的研究体系及计算结论为国内同类产品的开发与改进提供了建议与参考。