高速列车轮对多目标选配方法研究

马志颖，黎 荣，蔡子一

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

根据《铁路客车轮轴组装检修及管理规则》（以下简称《规则》）相关内容，轮对是指由一根车轴和两个车轮（含制动盘）采取过盈配合，经冷压装组成的整体车辆部件。根据实际生产情况，无论是新造轮对还是新旧轴零件混用的检修，零件的装配均采用了选配法[1-2]，即按经济精度制造，然后选择合适的零件进行装配，从而保证规定的装配精度的方法。

目前国内外学者在解决选配问题上进行了多种角度的研究。文献[3]建立了以装配封闭环间隙变化最小，余件最少的选配模型，使用NSGA-II 算法以活塞环与气缸的选配为例实现了优化；文献[4]立了田口质量损失函数最小的选配模型，使用人工免疫算法进行选配；文献[5]使用了集成精英策略的遗传算法重新进行分组，以适应非正态分布的零部件选配，并以球轴承组件为例实现了装配率的提高；文献[6]提出了高速列车轴承轴颈的智能选配方法；文献[7]提出了包括装配成功率、配合精度与质量波动的综合选配指标，并使用蚁群算法实现了多参数的曲柄组件选配优化；文献[8]应用了改进的多元质量损失函数进行选配优化。

综上所述，现有研究存在没有同时考虑质量损失与装配率，未考虑新旧零部件混用情况，以轮对选配过程为对象的研究较少等问题。为解决上述问题，通过结合高速列车轮对装配过程的特点与现有研究提出的选配需要考虑的各种因素，提出一种面向高速列车轮对装配的选配优化方法，构建优化轮对选配质量与装配率的多目标选配模型。通过改进的粒子群算法进行求解，从而得到良好的轮对装配方案，并通过轮对装配实例来验证该方法的有效性与可行性。

2 轮对零部件与装配要求分析

2.1 轮对零部件分析

根据《规则》中的相关定义，高速列车轮对的选配涉及制动盘、车轮与车轴三种零部件。参与轮对选配的每种零部件的参数之中有部分参数对于轮对的性能与质量有很大的影响，因此将这些参数作为关键参数进行分析。

根据文献[9]中的相关研究，在轮对的装配过程中涉及到的关键参数有轴身直径与空心轴孔径。此外制动盘座与轮座的尺寸影响到轮对装配精度，因此制动盘座与轮座的直径也属于关键参数。由于车轴两侧对称，上述参数（除空心孔径）在同一车轴上均有2 个；制动盘的内径与外径是其重要参数，外径的尺寸与制动力矩紧密相关，而内径则决定了制动盘能否可靠地固定在车轴上。此外，制动盘的厚度对于其性能也有影响。而盘内散热筋尺寸公差较大，且散热筋宽度影响到了制动盘厚的尺寸，因此采用散热筋宽度代替制动盘的厚度；根据相关研究[10]，车轮轮毂端头处的内外径与厚度属于重要参数，除此之外在《规则》中在轮对装配过程中对于轮径以及轮辋宽度也有要求。

2.2 轮对装配要求分析

2.2.1 装配尺寸链要求

由于轮对内侧距等装配重要参数还受到轮对压装操作的影响，不属于选配的范围，因此其装配尺寸链指车轴与车轮、车轴与制动盘的轴孔过盈配合。根据1.1 节的内容，涉及到装配的6 个参数构成了4 个装配尺寸链。由于高速列车的轴孔配合过盈量没有明确的规则要求，参考相关文献[11]中的说明，压装过盈量采用经验值，即按设计直径的（1.2～1.5）‰执行，而在合适的过盈量范围内越接近中间值的压装效果越好。

2.2.2 同轴零部件参数要求

选配时对于同轴相同零部件的部分参数有一定要求。通过《规则》与各参数的公差范围进行比较，发现对于高速列车轮对而言，只需额外保证同一车轴上的两个车轮直径差不超过0.3mm。由于车轮直径合格范围很宽，在全范围内进行无差别选配难以匹配合适的同轴车轮。为了提高车轮选配效率，需要在较小的范围内进行车轮选配，因此以0.5mm 为单位将车轮直径分组，仅考虑公差在其中一组（8600+0.50mm）范围内的选配。

3 轮对选配问题数学模型

装配质量受到选配情况的影响，在轮对的选配过程中，直接影响到其选配质量的因素包括零部件与装配尺寸链的质量，在一次选配中，装配出的轮对的质量应尽量平均；而轴孔的配合情况对轮对的质量也会产生影响，因此希望尽量提高一次选配过程中多个装配体的配合精度；此外装配率则影响到了选配的效率，也应该视为衡量选配质量的指标之一。因此以下从这三个方面建立高速列车轮对选配问题的数学模型。

3.1 基于信噪比的轮对多元质量损失函数

轮对选配中，多个关键参数都会影响到其质量，不同的参数对于轮对质量的影响程度也不同。而基于田口质量观的质量损失函数能够以定量的方式进行评价，并且广泛应用于选配问题中[7-8]。因此引入田口质量观，建立相应的质量损失函数来评价轮对的质量损失。由于组成轮对的零部件的参数均为望目特性，单质量损失函数，如式（1）所示。

式中：y—望目特性实际值；M—望目特性目标值。

对于只涉及零件本身的参数，目标值为参数设计尺寸值，对于关系到装配尺寸链的参数，将装配尺寸链封闭环的实际值作为质量特性进行计算，其目标值为采用规定过盈量的中值。

为了度量不同特性对总损失的影响，采用信噪比方式来建立多元质量损失函数。望目特性的信噪比计算方法，如式（2）所示。

式中：μ—望目特性的均值；σ2—望目特性的方差。

对于多元质量损失而言，由于信噪比的值越大，对应的质量指标越稳定，造成的损失就越小，据此判断质量指标的对于质量波动的“贡献”，并赋相应的权重。每个质量特性的权重计算公式，如式（3）所示。

式中：ηi—第i 个质量特性的信噪比；n—轮对质量特性数。

综上，基于信噪比的多元质量损失函数，如式（4）所示。

式中：L—总质量损失；n—质量特性的数目；yi—零部件第i 个质量特性的实际值。

以下在多元质量损失函数的基础上，构建零部件质量损失波动函数与封闭环的质量损失函数。

3.1.1 轮对零部件质量损失波动函数

针对轮对选配问题而言，任何组合的轮对零部件质量损失平均值不变，而且通过多次实验，发现使用平均离差表示每个轮对质量损失的偏离情况的优化效果优于方差，因此轮对零部件质量损失波动函数的计算公式构建如下：

式中：δ—轮对零部件质量波动值；n—一次选配能组成的轮对数；Li—第i 个轮对的零部件质量损失值；—所有轮对零部件质量损失平均值。

3.1.2 轮对封闭环质量损失函数

轮对的装配质量不仅受组成轮对的零部件的质量影响，还受到装配时的封闭环精度的影响。由前文可知轮对零部件关键参数分为两大种类，其一是只涉及到零部件本身的参数，其二是关系到装配尺寸链的参数，后者需要计算出封闭环尺寸，再通过得到的值计算装配体配合精度的质量损失情况。由前述可知轮对的装配尺寸链均为轴孔配合，因此每个尺寸链中封闭环的实际值计算方法，如式（6）所示。

式中：D—孔的实际直径；d—轴的实际直径。

由于单个轮对的装配精度由多个轴孔配合情况决定，因此在计算单个装配体的封闭环尺寸损失后，根据计算结果可以得出一次选配中所有轮对封闭环的质量损失之和ε，计算公式如下：

式中：LA，i—第i 个装配体的封闭环质量损失值；ε—轮对封闭环质量损失值；n—一次选配能组成的轮对数。

3.2 轮对装配率函数

在轮对的选配中，希望能够得到尽量多的装配组合，减少不匹配零件，以减少选配次数与时间，提高选配效率。轮对装配率φ可以定义为：

式中：S—装配成功的轮对个数；N—组成轮对的零部件组数。

3.3 轮对选配综合目标函数

轮对的质量损失与装配率共同评价轮对的选配情况，因此在选配中需要综合考虑质量损失与装配率对选配结果的影响，因此提出轮对选配综合目标函数，将选配目标综合为单一目标函数。式（9）、式（10）分别为为轮对选配综合目标函数与约束条件的计算公式。

其中，a、b、c 分别为装配质量与装配率的权重值，取值范围在（0，1）之间，且满足a+b+c=1，权重值的大小由实际情况确定。此外，式中装配率分子的改动是为了避免装配率为0 时导致目标函数总体分母为0。δ 为轮对零部件质量波动值；ε 为轮对封闭环质量损失值；φ 为装配率；分别为为质量特性的下限值与上限值（对于封闭环而言是过盈量的下、上限值），除封闭环外所有参数需要满足的约束，即零部件可用；Mi为第i 个质量特性的目标值，认为其等于质量特性上下限的中值；n 为一次选配能组成的轮对数；m 为轮对封闭环数；p 为轮对包含的零部件数，q 为一个零部件中包含的关键尺寸数。

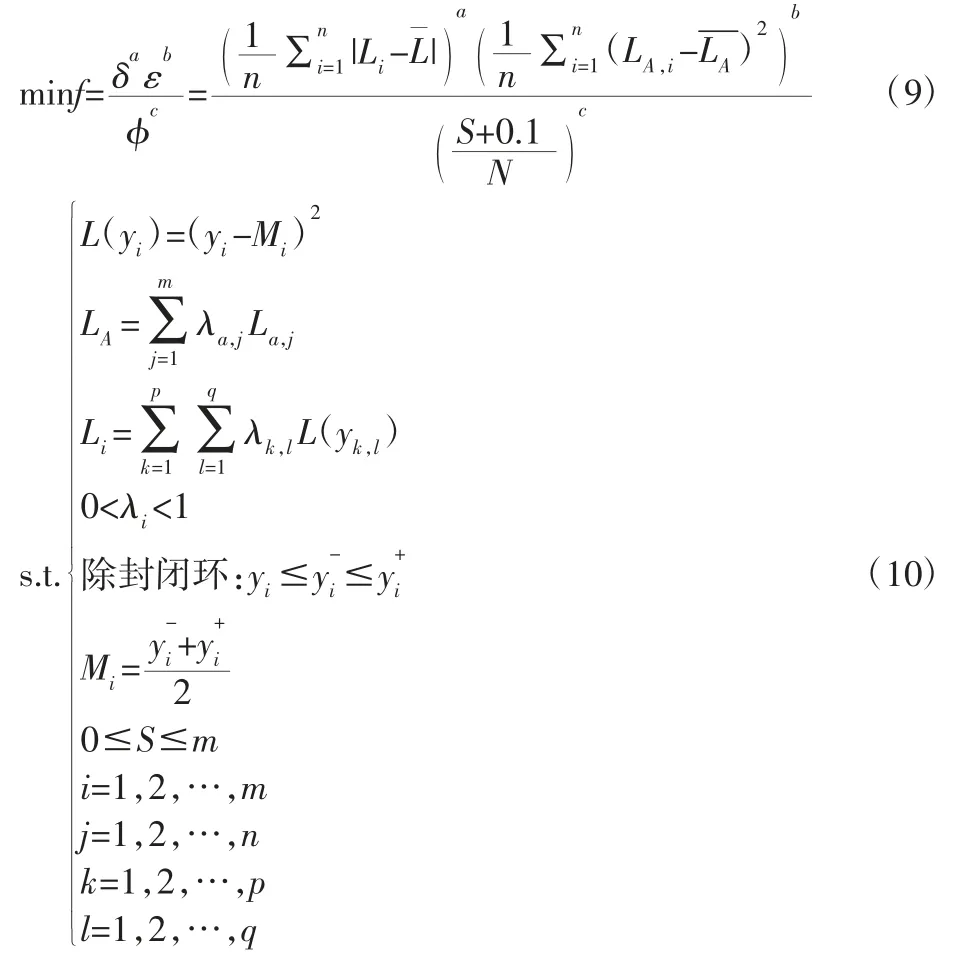
4 改进的粒子群算法求解

粒子群算法是一种模拟自然界鸟群、鱼群等生物群觅食行为机制的优化算法[12]，其基本原理是通过群体中不同的粒子的相互竞争与合作从而在寻优空间中找到所求问题的最优解。该优化方法具有构造简单、调节参数少、收敛速度快、易于实现的优点。

4.1 带压缩因子的粒子群算法原理

基本的粒子群算法首先是在寻优空间中随机生成一组初始粒子，每个粒子的位置代表一种可能的解。通过目标函数计算每个粒子的适应度，适应度的大小代表了粒子的优劣，并以此为依据选出目前粒子本身的最好位置（个体极值）与种群的最好位置（群体极值）。通过这两个极值改变粒子的飞行速度，从而更新粒子的位置直至到达规定的迭代次数。

设粒子群的规模为n，粒子的维数为m，最大迭代次数为p，其中在第t 次迭代中，第i 个粒子的位置表示为（t），…，xim（t）］，粒子速度表示为该粒子个体极值为pi=［pi1，pi2，…，pim］T，群体极值为pg=［pg1，pg2，…，pgm］T。

通过添加压缩因子的方式来提高粒子群算法的收敛速度和收敛精度[12]，在每次迭代中，粒子的速度与位置按照式（11）、式（12）进行更新：

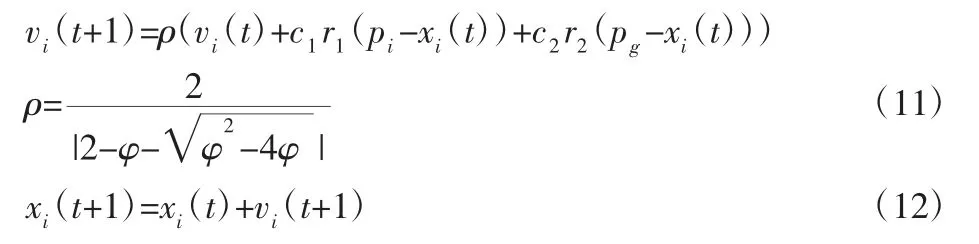
式中：ρ—压缩因子，满足ρ=c1+c2>4；c1，c2为学习因子，c1的值过大不利于算法的全局搜索，c2的值过大则容易陷入局部最优；r1，r2是范围在［0，1］之间的随机数。粒子速度更新的公式由三部分组成，第一部分是延续粒子上一次运动的惯性量；第二部分是向个体历史最优位置运动的个体认知量；第三部分是向群体最优位置运动的社会认知量。

对于轮对选配而言，粒子飞行改变的是零件编号的顺序，因此粒子群中解的更新应满足以下条件：①速度应该是在规定范围内的整数，即按式（12）求出速度值后四舍五入取整，由于速度值在编号的范围以内，据此再将超出范围n 的速度值除以n 取余数作为速度值；②由于解应在编号范围n 内，对于超出范围的解，小于0 的加上n，大于n 的减去n；③由于一个零件只能使用一次，每个编号在一个解中只能出现一次，因此在更新粒子群的位置后，需要判断是否存在重复与缺失的情况，并使用缺失的编号替换重复编号。

4.2 算法实现流程

带压缩因子的粒子群算法具有收敛速度快，精度高，适于求解轮对选配问题的特点，而通过综合目标函数的提出，使得该优化算法能够兼顾零部件质量损失的平衡、封闭环质量损失的缩减以及轮对装配率的保证。改进粒子群算法求解轮对选配问题的步骤如下，其具体流程，如图1 所示。（1）初始化种群。随机生成规定数目的粒子，从而形成初始种群，粒子的初始速度为0，个体极值为当前粒子本身，迭代次数为0。对于轮对选配问题而言，不同的粒子代表了不同的组合方式，即种群初始化时生成的是零部件不同顺序的排列情况。（2）更新群体极值。计算每个粒子的目标函数值，选择值最小的粒子作为群体极值。（3）粒子飞行。根据群体极值与个体极值，通过相应计算公式更新粒子的速度与位置。（4）更新个体极值。计算到达新位置的粒子当前的目标函数值，与原个体极值的目标函数值进行比较，将值较小的一个作为该粒子的个体极值。（5）判断迭代次数。达到要求次数则终止算法，输出群体极值作为优化结果，否则迭代次数加1，重复步骤（2）到步骤（5）的操作。

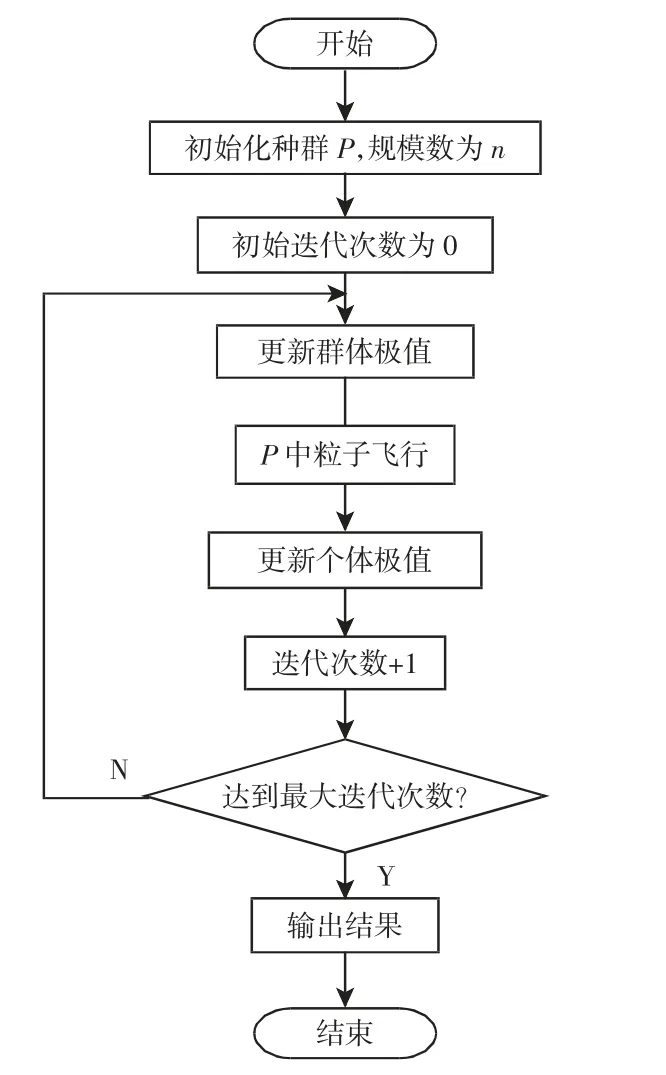
图1 改进粒子群求解轮对选配算法流程Fig.1 The Process ofImproved Particle Swarm Optimization Algorithm for Wheelset Selection

5 实例分析

为了验证第3 节中提出的方法的有效性，选取CRH2 的轮对作为研究对象，选择一定数量的车轴、车轮与制动盘进行优化计算。根据第2 节中轮对选配问题数学模型的描述，按照第3 节中的改进粒子群算法流程进行计算。在规定范围内随机生成的部分零件参数数据，如表1～表3 所示。根据选配过程中三个要素的重要程度，设定综合目标函数中权重值分别为a=0.1，b=0.6，c=0.3。改进的粒子群算法中的各项参数值分别为：c1=2.05，c2=2.05，由于问题规模较大，情况复杂，为了达到较为稳定的收敛结果，设定种群规模为100，迭代次数为400。使用python3.6.5 编写改进的粒子群程序进行相应的优化计算，在400 次迭代之后，结果收敛，得到一套综合最优的选配组合，如表4 所示。对应的轮对选配综合目标函数值为0.5814，对应的装配率为100%，零部件质量损失波动值为0.0472，封闭环的质量损失值为0.6820，目标函数值的优化趋势，如图2 所示。

表1 部分车轴参数Tab.1 Partial Axle Parameters

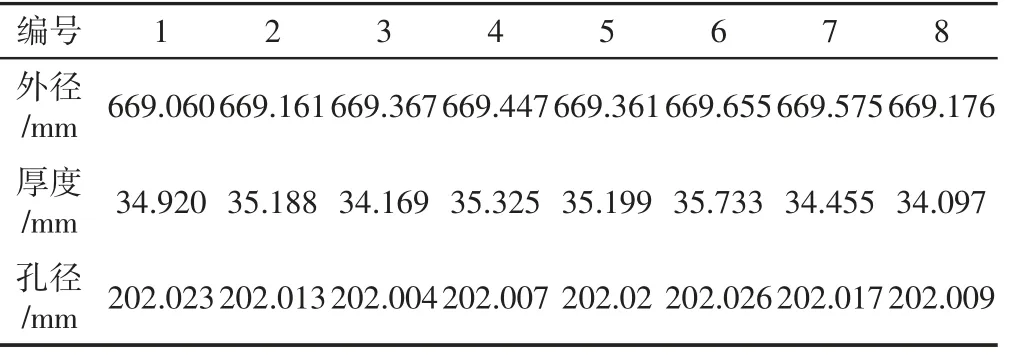
表2 部分制动盘参数Tab.2 Partial Brake Disc Parameters

表3 部分车轮参数Tab.3 Partial Wheel Parameters

表4 多目标优化选配结果Tab.4 Optimizing Selection Result with Mutil-objective

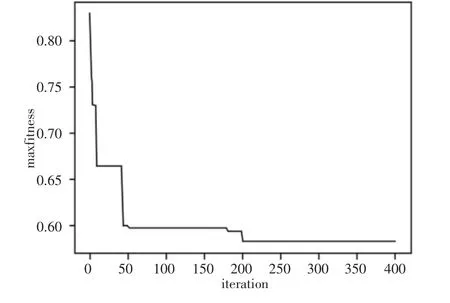
图2 目标函数值趋势图Fig.2 Trend of Object Function Values

由于实际生产中的轮对选配一般是单个轮对逐步进行选配，为了能够进行比较，随机生成一组选配组合，其组合方式，如表5 所示。该种选配的轮对选配综合目标函数值为1.2626，对应的装配率为75%，零部件质量损失波动值为1.4508，封闭环的质量损失值为1.2203。

通过图2 可以发现：

（1）粒子群算法梯度下降寻优；

（2）在给出的轮对零部件数据与相应权重下，通过选配优化方法能够在较大程度上同时提高了多个轮对的质量（相比随机选配，零部件质量损失波动下降了96.75%，封闭环质量损失下降了44.11%），并且保证装配率（优化后全部零件均能进行装配），减少零件浪费；

（3）多次实验的结果表明该方法在轮对零部件尺寸参数波动较大的情况下能得到更稳定的结果，参数波动小时结果虽然会产生多种组合情况，但每种组合的装配质量都能达到满意的结果；

（4）实验结果表明该方法能在较短的迭代次数（400 次）与较短时间内得到优化结果，可以应用在实际生产之中。

实验结果表明，在装配率、零部件质量损失波动与封闭环质量损失三个指标中，研究中提出的优化方法均得到了良好的优化结果。

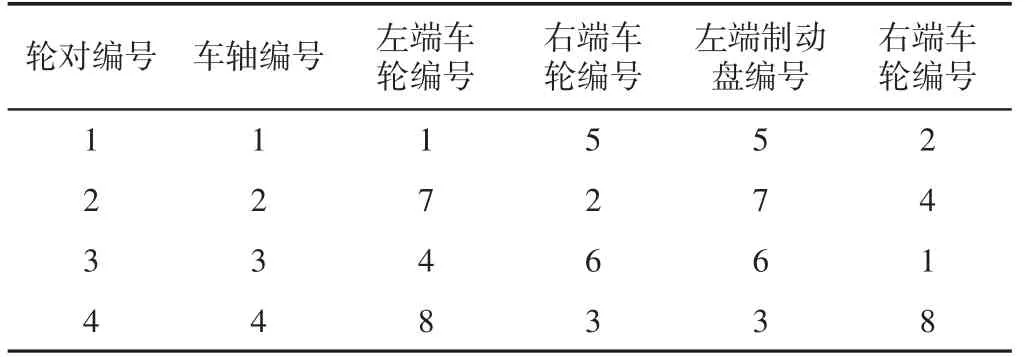
表5 随机组合选配结果Tab.5 Selection Result of Random Combination

6 结论

提出的高速列车轮对多目标选配方法能够在合理的时间内得到多组质量较均衡、装配质量高的轮对，零部件参数波动越大，优化效果越好。适合在实际生产中用于提高工厂装配质量与效率，尤其适用于新旧混用的轮对装配中。根据使用情况的不同，需要相应地改变权重值从而得到更合适的优化结果。但在零部件参数波动很小时得到的优化解较难稳定，在接下来的研究中需要解决这一问题。

为了优化轮对选配的效率与质量，提出了一种综合考虑零部件质量损失波动、封闭环质量损失与装配率的数学模型，通过带压缩因子的改进粒子群优化算法进行轮对选配问题的优化，通过轮对选配实例验证了该模型与算法的有效性，并且最终取得了良好的优化效果。建立的模型实现了多组轮对同时优化，在保证选配质量的同时也能达到较高的装配率，同时该模型对于其他复杂零部件的选配优化也有一定参考价值。