探究无穷限广义积分的计算方法

陈 飞

(商丘职业技术学院，河南 商丘 476100)

微积分学习中,广义积分的概念比较抽象,与定积分的求法差异较大，是微积分学习的一个难点.无穷限广义积分计算的方法多种多样,合理的运用计算方法可以降低求解问题的难度.本文就无穷限广义积分常用的求解方法进行分析探讨,并结合具体例题进行讲解.

1 无穷限广义积分的概念

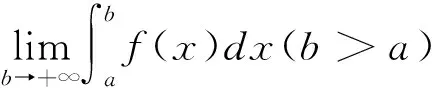
2 几种计算方法的解析

2.1 运用定义进行求解

无穷限广义积分的求解可以借助其定义,按照求定积分的方法求出原函数,然后取极限,进而判断其敛散性及求值.

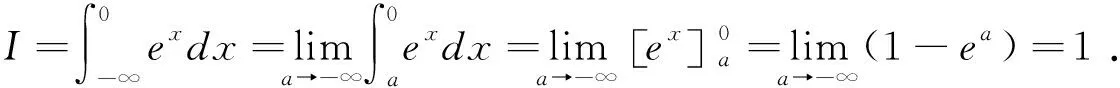
为了书写简便,广义积分的计算过程可仿照牛顿—莱布尼兹公式简记为

其中F(x)是f(x)的一个原函数.

按照这种简便书写格式，例1的计算过程可写为

2.2 运用等量代换进行求解

在运用定义法求广义积分时,有时被积函数不容易求得,这时,可以借助等量代换的方法.在等量代换时,要注意被积函数和积分上下限的变换.

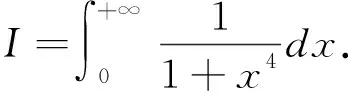
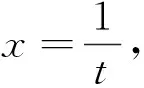
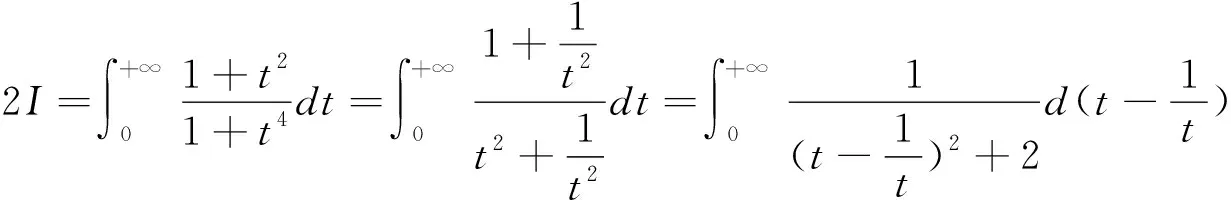
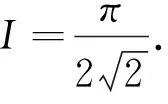
2.3 运用二重积分进行求解

对于一些类型的广义积分,可以通过变换，把广义积分巧妙地化为一个二重积分.然后,计算二重积分,从而间接地计算出广义积分的值[2]19-22.

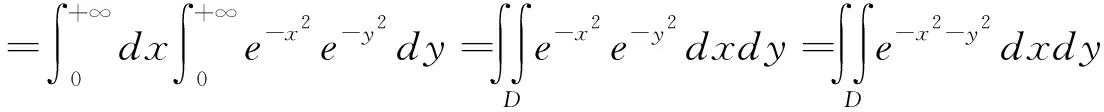
再转化为二重积分的极坐标进行计算

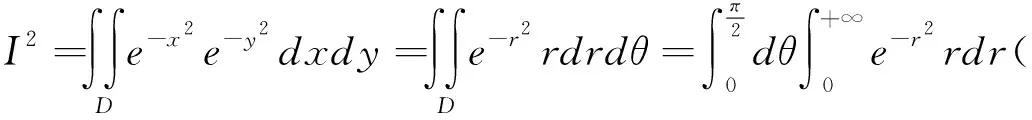
2.4 积分号下求导法计算无穷限广义积分

这种方法是对被积函数引入一个收敛因子,因子中有一个参数,对参数求导,有时可求得原积分的值.在此情况下引入的收敛因子加强了原积分的收敛性.这样使积分号下求导条件得以满足.一般采用e-kx(k>0)作为收敛因子[3]84-86.

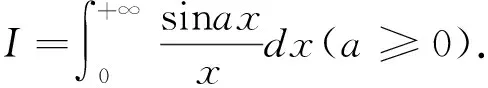
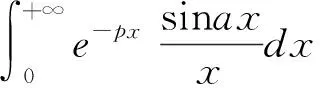
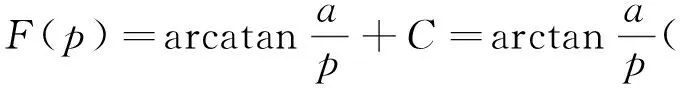
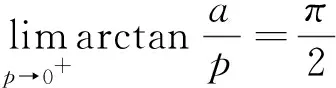
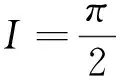
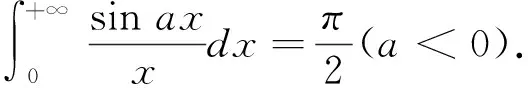
2.5 积分号下求积分法计算无穷限广义积分

这种方法是将被积函数中某一因子表示为一个适当的积分.于是将原积分化成二次积分，交换这两个积分的顺序,就可求出所给的积分.

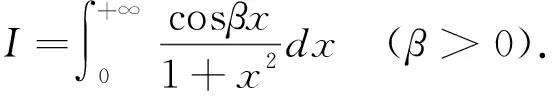
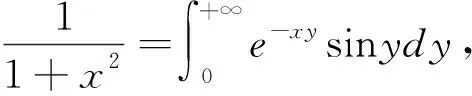
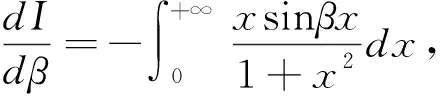
所以I=Ce-β，为了确定C,令β=0.

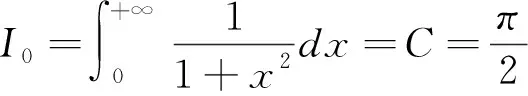
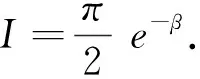
2.6 运用Laplace变换进行求解

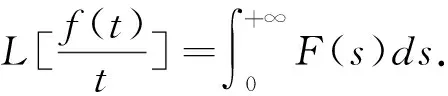
由Laplace变换的定义及积分性质可得

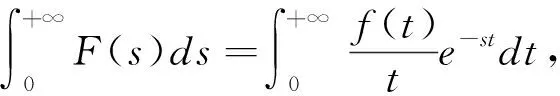
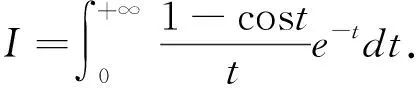
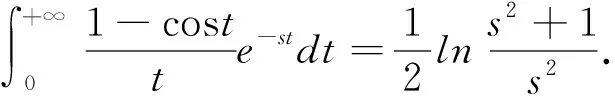
2.7 运用级数展开法进行求解

对于一些类型的广义积分,可以通过将被积函数展成级数,或者将无穷区间上的广义积分表示成级数的形式进行求解[5]67-69.

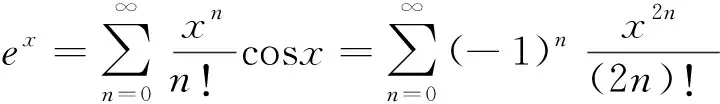
2.8 运用概率密度函数性质进行求解

设连续型随机变量X,服从参数μ,σ2(σ>0)的正态分布[5]67-69.

其概率密度函数为

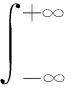
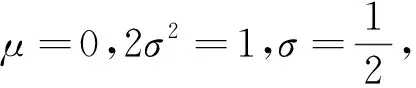
2.9 运用留数计算进行求解

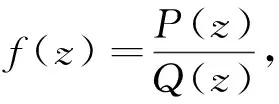
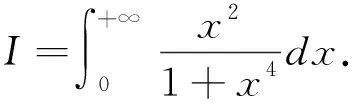
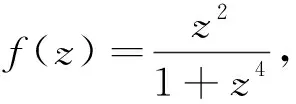
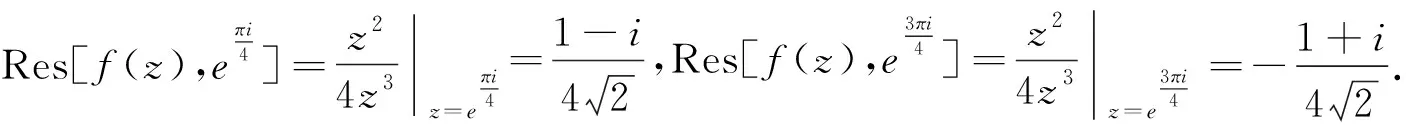
由于被积函数为偶函数,故

3 结语

无穷限广义积分是积分知识的一个难点.针对不同形式的无穷限广义积分,在求解过程中,我们可以借助相关的数学知识,采用多种方法进行求解.本文介绍了几种常用的求解方法,对解决相同类型的无穷限广义积分具有现实意义.