非溶解性危险化学品在内河中的泄漏扩散规律

詹水芬，王明超 ，陈学民 ，蒋文新

（1. 兰州交通大学 环境与市政工程学院，甘肃 兰州 730070；2. 交通运输部天津水运工程科学研究院，天津 300456；3. 天津东方泰瑞科技有限公司，天津 300192）

非溶解性危险化学品（危化品）一旦在内河中泄漏将形成危化品泄漏团，造成水体以及沿岸环境的污染［1］。开展内河船运危化品泄漏扩散规律研究，预测危化品泄漏区域变化范围，对于事故应急处置及危化品回收等具有重要的意义。KACHIASIVILI等［2-3］利用扩散模型对危化品在水体中的扩散情况进行了研究。DUAN等［4］设计实验模拟了危化品在弯曲水槽中的流动和扩散过程。部分学者对内河溢油的特殊情况建立了扩散模型，采用不同方式对数值模型进行求解［5-7］。SONG等［8］探讨了柴油泄漏事故对河水及周围环境的污染情况。有学者探讨了感潮河网和河口溢油事故的扩散运输过程［9-10］，但研究成果主要针对海上溢油事故［11-15］。屈长龙等［16-17］对甲醇泄漏进行了数值模拟研究。王冰等［18-19］利用IWIND-LR模型对油品在内河中的迁移过程进行了快速模拟。闫洁洁等［20］使用ALOHA软件对泄漏的液氯进行量化模拟，可准确快捷地评估液氯泄漏对周边环境的影响。但内河危化品泄漏扩散的研究仍存在不足：1）内河水面危化品的泄漏扩散研究较少；2）危化品泄漏团的尺寸、个数以及影响范围等未做深入研究。

本工作对非溶解性危化品在内河中泄漏扩散过程进行数值计算，对危化品的泄漏、漂移和扩散过程进行研究，分析危化品泄漏扩散范围随时间的变化规律。

1 危化品泄漏扩散模型

1.1 泄漏区域

内河中危化品运输船舶与其他物体（船舶、桥墩等）发生剐蹭/撞击后，可能会将船舶撕开一个泄漏口。此时，船舶内储存的危化品将从泄漏口流出，进入内河水体。当危化品密度小于水的密度且不溶于水时，泄漏的危化品将漂浮在水面，形成危化品的泄漏团，并随河水向下游流动。针对内河船舶危化品泄漏扩散问题，同时考虑到河道边界的不规则性，本研究利用地图软件获取河道区域的卫星地图，采用绘图软件对河道、船舶以及建构筑物等进行准确刻画，获得了完整的二维内河危化品运输船舶泄漏扩散区域。危化品内河运输泄漏扩散区域见图1。由图1可见：黄色实线围成的区域为危化品泄漏扩散区域，长度约4.0 km，河面宽度约1.0 km；河道中有一艘3 000 t的危化品运输船舶，位于区域上游，船舶长宽分别为81.0 m和13.6 m；由于船舶碰撞剐蹭等原因，船尾部出现了1.0 m的泄漏口。

图1 危化品内河运输泄漏扩散区域

1.2 数学模型

内河非溶解性危化品泄漏后将漂浮在河面上，形成危化品泄漏团的泄漏带。采用流体体积（VOF）方法捕捉危化品泄漏团的泄漏、漂移和扩散过程。内河危化品运输船舶的实际尺寸较大，危化品泄漏过程中雷诺数Re较高，流动过程属于湍流。例如，对于3 000 t级的柴油船舶，当泄漏口尺寸为1 m、泄漏流速为1.5 m/s时，危化品泄漏过程Re约为4.0×105，流动属于湍流。基于此，本研究采用标准k-ε模型模拟其湍流过程。内河危化品泄漏扩散控制方程见式（1）～（3）［21］。

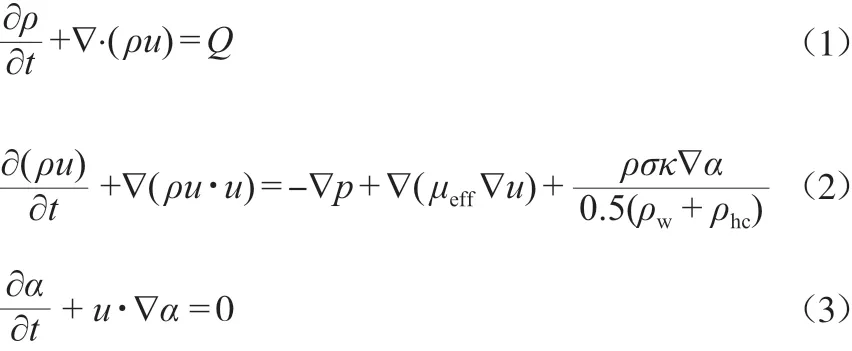
式中：ρ为危化品密度，kg/m3；t为泄漏时间，min；u为危化品泄漏扩散速度，m/s；Q为危化品泄漏流量，kg/s；ρw为水的密度，kg/m3；p为水的压力，Pa；ρhc为危化品密度，kg/m3；μeff为有效黏度，Pa·s，由μeff=μ+μtur计算，其中，μ为流体动力黏度，μtur为湍流黏度；σ为危化品表面张力，N/m；κ为界面曲率，1/m，κ= Δ·n，n为界面法向量，由计算［19］；α为控制容积中水相的体积分数，%。

内河危化品泄漏过程中，计算区域的危化品体积分数将发生变化，从而导致区域流体物性密度、黏度发生变化，本研究中将采用式（4）和式（5）来计算。

式中，μw和μhc分别为水和危化品的黏度。

计算区域内的流动状态属于湍流，可采用标准k-ε方程分别计算湍动能k、湍动能耗散率ε和湍流黏度μtur，见式（6）～（8）。

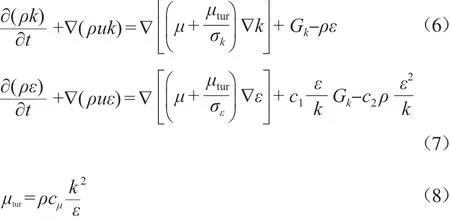
式中：c1，c2，cμ，σk，σε均为常数，其取值分别为1.44，1.92，0.09，1.0，1.3；Gk为湍动能生成项，其计算式为Gk=μturS2，其中，S为平均形变速率张量的模，Sij为形变速率张量，s-1。

1.3 边界条件和初始条件

1.3.1 边界条件

边界条件包括河流边界条件和船舶边界条件。对于河流边界条件，计算区域左边界为速度入口边界且入口流速恒定，河流沿岸为无滑移边界，计算区域右边界为速度出口边界。对于船舶边界条件，船尾部危化品泄漏口为速度入口边界，船体其余部分为无滑移边界。

1.3.2 初始条件

初始时刻，危化品还未泄漏，计算区域内只有河水流动，且流动过程达到稳定。在某个时刻，船尾部泄漏口处开始有危化品流出，计时从此开始。

2 数值计算方法和算例设置

2.1 数值计算方法

在本文计算中，压力和速度采用SIMPLE算法耦合，对流项和扩散项分别采用二阶迎风格式和中心差分格式离散，非稳态项采用全隐格式离散，收敛标准为连续性方程余量和动量方程余量同时小于1.0×10-5。

2.2 算例设置

在算例设置之前，首先要选取计算区域。本研究中选择长江主干线南京段八卦洲北汊河段为计算区域，如图1所示。其中，河流上游为散货码头，河流下游为中国石化扬子石化公司危化品运输码头，主要开展石油类危化品储存、运输以及装卸等作业。以长江水上事故救援机制和能力作为参考，本研究中设置危化品泄漏时间为30.0 min。

采用三角形网格离散整个计算区域，计算区域的网格分布见图2。如图2所示，在船舶附近尤其是船尾泄漏口处网格加密，泄漏口处网格尺寸取0.05 m。通过对多套网格和多组时间步长试算结果的比较，选取总网格数为199 615，时间步长为0.1 s。

3 计算结果与分析

3.1 模型验证

液态非溶解性危化品在水体中泄漏、扩散数值模拟的关键是两种非互溶液体物质的相互作用。本研究采用标准k-ε模型描述这一泄漏、扩散过程，并采用经典的方腔内液柱倒塌算例来验证模型的正确性。本文计算的液柱底部水平方向长度随时间的变化曲线见图3。由图3可见，本文计算结果与文献结果［22-23］吻合良好。

3.2 危化品泄漏扩散规律研究

危化品泄漏扩散范围的准确确定对于泄漏危化品的围控、事故应急处置以及后续连锁事故的预防具有重要的意义。对危化品泄漏扩散过程进行计算的模拟结果见图4。由图4可见，在泄漏初期，最大泄漏团面积随泄漏时间的延长近似均匀增大，增长率约为34.42 m2/min，到泄漏25.0 min时，最大泄漏团面积已经超过900 m2。由图4a可见，危化品从泄漏口流出后，在河水冲击作用下在船尾部堆积、拉伸，最终形成椭圆形的危化品泄漏团。此时危化品泄漏团尚未脱离泄漏口，如图4b所示。随着泄漏过程的继续进行，泄漏出来的危化品在泄漏速度和水流速度的共同作用下开始顺时针旋转，并向河流下游漂移，如图4c和图4d所示。在这一阶段，椭圆形的危化品泄漏团继续快速旋转，逐渐恢复成圆形，直径达到20 m，直至完全脱离泄漏口。从泄漏口释放的危化品泄漏团为主泄漏团。当主泄漏团脱离泄漏口后，位于边缘处的部分危化品将被甩出，在泄漏团周围形成一圈规则的危化品液滴尾迹，如图4e所示。随着泄漏过程的进行，河水也会被卷入危化品主泄漏团中，形成危化品与河水的混合物。随着泄漏团的旋转，泄漏团被撕裂，河水又被释放，不规则的危化品泄漏团逐渐形成，见图4f～图4h。此时，主泄漏团及其周围的危化品液滴出现了分裂和融合，危化品与河水的流动过程趋于复杂。总体来看，危化品持续不断地从泄漏口流出，在下游河道中形成了一系列近似规则的危化品泄漏团分布，如图4e～图4h，直至船舶内危化品完全泄漏。

图2 计算区域的网格分布

危化品泄漏区域长度和宽度随泄漏时间的变化见图5。由图5可见，随着泄漏时间的延长，危化品泄漏团泄漏区域的长度和宽度均逐渐增大，平均增长速率约为0.65 m/s和0.10 m/s。分析其原因可知，泄漏团释放后漂浮在水面，且以顺时针旋转的方式随水流向河流下游流动，因此，泄漏区域长度平均增长速率与水流速率（0.5 m/s）存在一定的差异。而且，当泄漏团到达河道转弯处时（距离泄漏口约900 m），在离心力、泄漏团内聚力以及泄漏团之间的黏滞力的共同作用下，泄漏区域长度增长过程明显变慢。在泄漏区域宽度变化方面，由于危化品泄漏团在向内河下游漂移时会发生顺时针的旋转并甩出危化品液滴，同时因受到河水流动的冲击作用，主泄漏团和危化品液滴的纵向扩散过程受到抑制。此外，危化品泄漏团在漂移时还会发生泄漏团的融合。在这些因素的综合作用下，泄漏区域宽度表现出波动式增长的特点。

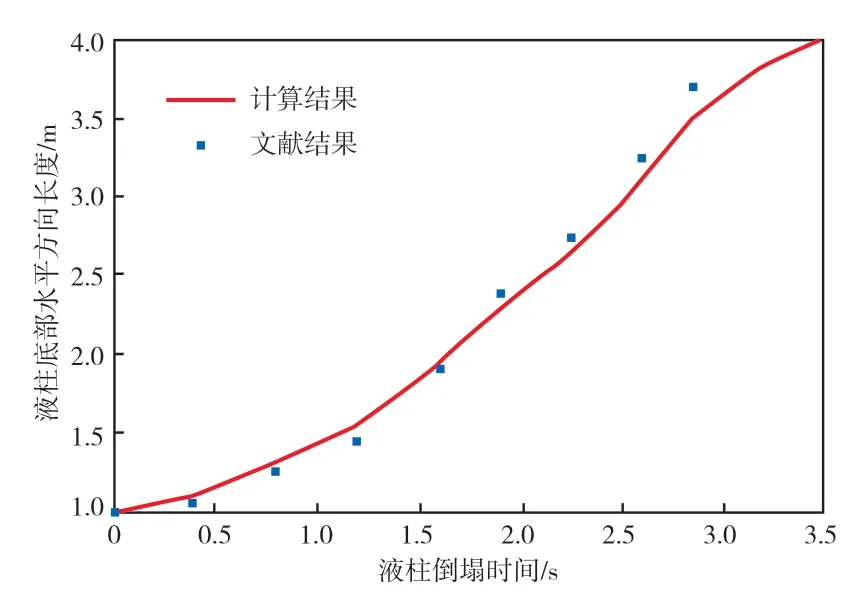
图3 液柱底部水平方向长度随时间的变化曲线

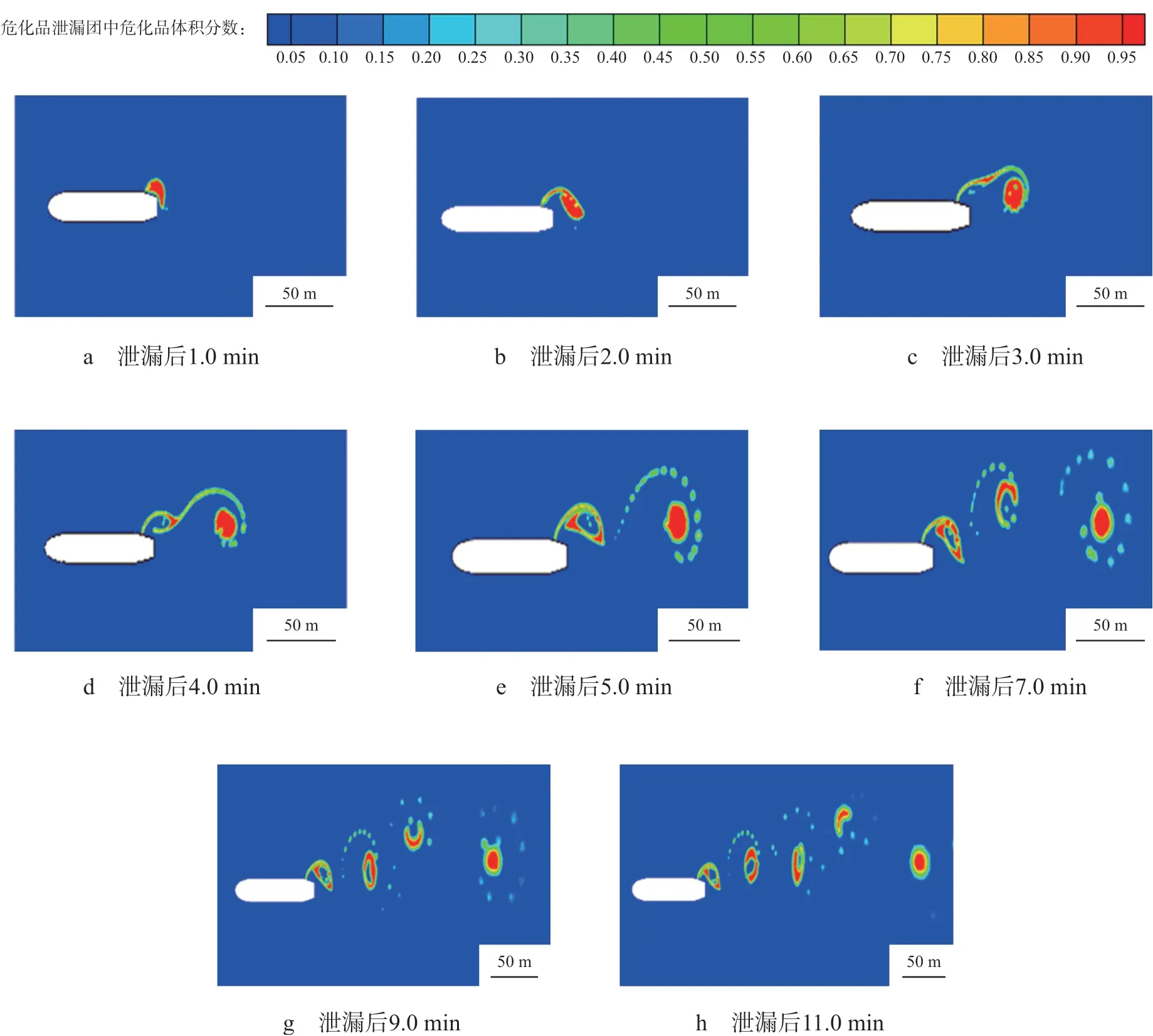
图4 危化品泄漏和扩散过程模拟结果

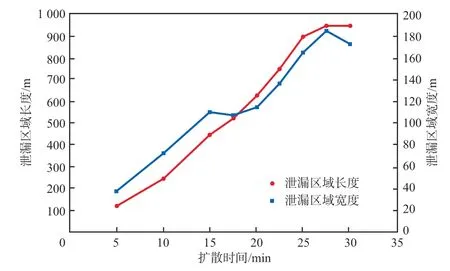
图5 危化品泄漏区域长度和宽度随泄漏时间的变化

危化品泄漏团数量和最大泄漏团面积能够反映泄漏危化品的危险程度。危化品泄漏团数量随泄漏时间的变化见图6。由图6可见，泄漏危化品泄漏团数量随泄漏时间表现出逐渐增加的趋势。

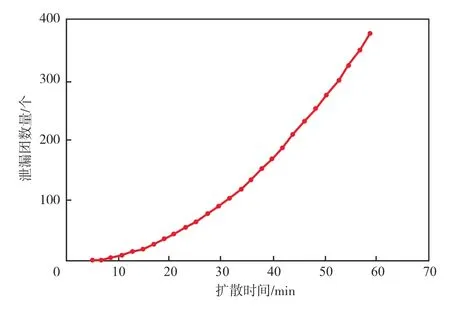
图6 危化品泄漏团数量随泄漏时间的变化

危化品泄漏后泄漏团数量和最大泄漏团面积的变化见图7。

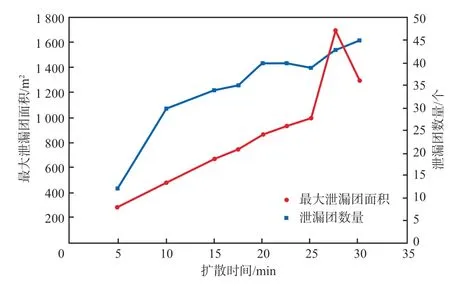
图7 危化品泄漏后泄漏团数量和最大泄漏团面积的变化

由图7可见：在泄漏初期，泄漏团面积较小，旋转速率较大，泄漏团融合仅发生在主泄漏团和被甩出的危化品液滴之间，泄漏团面积变化不大；随着泄漏时间的延长，泄漏团旋转速率逐渐减小，泄漏团面积逐渐增大，主泄漏团之间的融合过程加速，导致泄漏团数量增长率逐渐减小，最大泄漏团面积快速增大；到泄漏27.5 min时，泄漏团数量超过40个，最大泄漏团面积接近1 800 m2，事故风险增大。随着泄漏时间延长，泄漏团在多个作用力下逐渐分解成多个小的泄漏团，最大泄漏团面积逐渐减小。

4 结论

a）针对内河非溶解性危化品运输船舶泄漏后危化品的泄漏扩散规律进行数值模拟计算，计算结果与文献记录结果吻合度高。将该法应用到内河化学品泄漏扩散结果的预测和评估过程，有利于发生泄漏后应急措施的尽早决策。

b）危化品从船尾泄漏口流出后将形成一系列大小不一、形状各异的泄漏团。泄漏团释放后，将以顺时针旋转的方式向河流下游漂移，并甩出大量危化品液滴。随泄漏时间的延长，泄漏团面积逐渐增大，到泄漏25.0 min时，未融合的最大泄漏团面积超过900 m2。此外，当泄漏团靠近河道转弯处时，泄漏团将发生融合。泄漏后27.5 min时，泄漏团数量超过40个，最大泄漏团面积接近1 800 m2，次生事故风险显著增加。

致谢 本研究得到中央级公益性科研院所基本科研业务费专项资金项目（TKS190114）支持。