计及电动汽车充电与可再生能源协同调度的负荷特性分析

赵滨滨，王莹，徐晓萌，王彬，宣文博，雷峥，葛磊蛟

(1.国网天津市电力公司，天津300055;2.国网天津市电力公司 经济技术研究院，天津300171;3.天津大学 电气自动化与信息工程学院，天津 300072)

0 引 言

近年来，我国的间歇式可再生能源发展迅速,截至2018年6月底，我国的风电装机容量超过了1.7×108kW，光伏发电装机容量超过了1.5×108kW，风电、光伏发电装机容量均位居世界第一。然而，风电、光伏等具有强随机性的可再生能源发电并网后会对电网功率产生波动，如何平抑大规模可再生能源入网引起的功率波动和提高可再生能源消纳能力，是一个亟待解决的问题[1-2]。

另外，电动汽车作为一种绿色环保的交通工具，近年来得到国家政策的大力扶持。截至2017年底，我国电动汽车保有量已超过150万辆，到2020年预计超过500万辆。然而，电动汽车的充电时间具有一定的随机性和聚集性，大规模电动汽车无序接入，可能会加大电网负荷的峰谷差，增加电网运行的成本。因此，如何通过协调控制电动汽车的充电过程，减少其对电网的影响，也是值得研究的问题[1，3]。

针对上述两个问题，学者们提出如下解决思路：通过协同调度电动汽车充电与可再生能源发电，引导电动汽车有序充电以减少其对电网的冲击，同时平衡可再生能源发电对电网造成的波动[4-8]。于大洋等[5]以减少电网等效负荷的波动为目标，提出电动汽车与风电协同调度的数学模型，分析了调度电动汽车充电以平滑电网负荷波动、消纳风电的可行性；谢小英等[6]将电动汽车可用充放电容量作为快速响应的可调度负荷，以净负荷波动差最小为目标，提出了一种电动汽车有序充放电策略；葛少云等[1]建立了峰谷电价模型，从需求侧管理出发，引导电动汽车有序充电，达到平抑电网因大规模风、光发电接入而产生的波动和优化电网峰谷差的目的；侯建朝等[7]建立计及需求响应的风电与电动汽车协同调度的多目标优化模型，通过价格机制引导电动汽车入网，以负荷方差最小为主要目标，协调优化电动汽车和发电侧资源，以实现消纳风电和平抑负荷波动；段小宇等[8]在建立节点充电负荷模型的基础上，提出了电动汽车充电负荷、可再生能源与无功补偿装置的配电网两阶段优化策略，利用电动汽车的灵活充电特性减少配电网的波动。上述研究针对如何应用电动汽车平抑可再生能源和负荷波动的问题进行了有益的探索，然而，这些研究仅侧重于从调度控制或需求侧响应的角度分析电动汽车有序充电的方案，并未对电动汽车有序充电后电网和电动汽车的负荷特性进行研究，从而无法准确评估电动汽车与可再生能源协同调度的效果和影响。

基于以上分析，本文针对电动汽车与可再生能源协同调度后电网和电动汽车的负荷特性进行研究。首先，分析电动汽车无序充电和可再生能源接入对电网负荷特性的影响；其次，以减小净负荷波动、降低峰谷差为目标，建立电动汽车与光伏发电协同调度的数学模型；然后，建立负荷特性评价指标体系，用以评价电动汽车响应电网调度、平抑可再生能源出力波动的效果；最后，通过天津市某区域的实际数据进行仿真试验，验证所提电动汽车与光伏发电协同调度数学模型的有效性，并基于所建立的负荷特性评价指标体系，分析协同调度后电网和电动汽车的负荷特性。

1 电动汽车无序充电和可再生能源接入对电网负荷特性的影响

1.1 电动汽车无序充电对电网的影响

电动汽车作为一种特殊的负荷，在充电方式、充电地点及充电时间等方面都有很大随机性，其充电状况与车主用户行为、电力价格及政府调控策略有很大联系，负荷特性较为复杂[9]。当大规模电动汽车进行无序充电时，会对电网负荷产生极大冲击。以每个季节中的最大负荷发生日作为各季节的典型日，以天津市某区域的商业负荷、工业负荷、居民负荷之和为基础负荷数据，当该区域的电动汽车无序充电时，分析该区域各季度典型日的负荷波动，具体如图1所示。

由图1可看出，该算例中电动汽车无序充电的负荷需求峰值均出现在各季节典型日基础负荷的峰值附近，使电网的最大负荷产生一定增长，导致电网峰谷差变大。经统计，电动汽车接入后，该区域峰谷差平均增加了10.4%，峰谷差最大增加比达27.8%，负荷率平均下降了4.7%，电网负荷特性恶化。可见，如果不对电动汽车的充电加以引导，在电动汽车大规模无序接入的情形下，有可能会拉大电网的峰谷差，这不仅增加了电网正常备用容量的需求，而且也对输配电网络的容量提出了更高要求，导致电网运行的经济性下降。

1.2 可再生能源接入对电网的影响

风电、光伏发电等可再生能源受地理位置、气象因素等影响，往往具有较强的波动性和不确定性，其大规模并网可能影响电网的安全稳定运行[10]。本文以光伏发电为例，分析其接入电网后对电网负荷特性的影响。以天津市某区域各季度典型日负荷曲线为基础负荷曲线，结合接入该区域的光伏发电功率曲线，得到电网净负荷曲线，如图2所示。

其中，净负荷为

图2 光伏发电接入后电网的负荷曲线

Fig.2 Grid load curves after PV power generation accessed

Pnet=Pl-Ppv，

(1)

式中，Pnet、Pl、Ppv分别为叠加光伏发电功率后的电网净负荷、基础负荷和光伏发电功率。

由图2可看出，光伏在白天输出功率，且功率曲线波动较大。接入光伏后，与原基础负荷曲线相比，电网的净负荷曲线在部分时段幅值有所下降，负荷峰值及其出现的时间发生了改变，负荷曲线发生较大的波动。

1.3 电动汽车无序充电和可再生能源接入下电网的净负荷特性

当同时考虑电动汽车无序充电和光伏发电接入时，电网的净负荷曲线如图3所示。此时，叠加光伏发电功率和电动汽车无序充电负荷后的电网净负荷为

Pnet=Pl+Pev-Ppv，

(2)

式中，Pev为电动汽车无序充电功率。

由图3可看出，在电动汽车无序充电，同时考虑光伏发电接入的情况下，电网净负荷曲线峰值增高，波动性变强。经统计，两者同时接入使该区域负荷峰谷差平均值增加了8.8%，负荷率下降了3.9%。此时的净负荷与仅考虑电动汽车无序充电的情况相比，负荷特性稍好，说明该区域中电动汽车充电行为与光伏发电有一定的天然耦合性。但与基础负荷相比，同时考虑电动汽车无序充电与光伏发电接入的情况下，净负荷特性仍然较差。

图3 同时考虑无序充电和光伏发电接入的净负荷曲线Fig.3 Net load curves considering disordered charging and PV power generation

由以上分析可知，光伏发电并网和电动汽车无序充电使电网调度面对的净负荷曲线峰谷差变大，波动性也变强，这增加了电网调度的难度，降低了电网运行的稳定性和经济性。

2 电动汽车与可再生能源协同调度模型

已有文献统计表明，每辆电动汽车平均每天将有95%以上的时间是处于空闲状态的，具备较强的可调度性[11-13]，若能够对其充电过程加以引导，在电网净负荷低谷时充电，不仅可以起到削峰填谷的作用，而且还可以平衡可再生能源带来的功率波动[14-16]。对此，本文以电动汽车和再生能源中的光伏发电为研究对象，研究电动汽车有序充电方案，提出电动汽车-光伏发电协同调度模型。

结合电动汽车充电负荷、光伏发电和电网常规基础负荷之间的协同性和互补性，通过调控电动汽车的充电行为，实现电动汽车-光伏发电协同调度，可以提高光伏发电的利用率，减少电网的峰谷差率。以净负荷方差最小为目标函数，建立电动汽车有序充电模型如下，

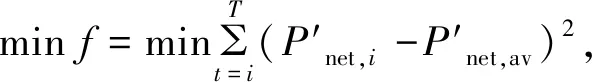
(3)

(4)

P′net，i=Pl，i+P′ev，i-Ppv，i，

(5)

式中：t为电动汽车参与协同调度的起始时刻；T为一个协同调度的周期；P′net，i为电动汽车有序充电时系统净负荷在i时段的功率值；Pl，i为系统基础负荷在i时段的功率值；P′ev，i为电动汽车有序充电在i时段的功率值；Ppv，i为光伏系统出力在i时段的功率值。

模型中，电动汽车电池剩余能量可表示为

Si+1=Si+λchaP′ev，iΔt-Pdch，iΔt，

(6)

式中：Si+1和Si分别为第i时段和第i+1时段电池剩余能量；Δt为时间间隔；λcha为电动汽车的充电效率；Pdch，i为i时段电动汽车的耗电功率。

第i时段电池剩余能量的不等式约束为

Smin≤Si≤Smax,

(7)

式中，Smax和Smin分别为电池存储能量的上、下限。

每个时段可调度的电动汽车充电功率有一定的限制范围，该范围取决于各时段可调度的电动汽车数量，由可自由充电情况下的电动汽车充电功率乘以一定的裕度表示，即

ηmin.Pev，i≤P′ev，i≤ηmax.Pev，i,

(8)

式中：ηmax和ηmin分别为充电裕度的最大、最小值；Pev，i为电动汽车无序充电在i时段的功率值，该值可由对电动汽车充电功率进行日常预测得到。

在一个调度周期内，电动汽车无序充电与有序充电的充电总需求相等，约束等式为

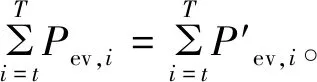
(9)

综上，由式(3)～(9)构成了电动汽车-光伏发电协同调度模型。模型中，P′ev，i为优化变量，其余的参数均假定为已知量。

3 电动汽车协同调度的负荷特性指标

电动汽车可以通过上文建立的协同调度模型来响应电网的调控信号，从而实现有序充电，平衡可再生能源给电网带来的波动。然而，对于电动汽车响应的效果，现有文献大多仅用负荷的峰谷差这单一指标表示，难以准确反映电动汽车响应后负荷的特性，也无法全面评估电动汽车响应的效果和影响。对此，本文提出电动汽车响应效果评价指标体系，以期能全面准确地评价电动汽车协同调度的效果。

3.1 电网负荷特性指标

本文采用负荷率、峰谷差、负荷波动率这3个指标反映电网的负荷特性。通过对比电动汽车响应前后电网负荷这3个指标的变化，就能得到电动汽车与可再生能源协同调度后电网负荷特性的变化情况。

3.1.1 负荷率

负荷率K用于描述负荷曲线特性，表征一天中负荷的不均衡性，较高的负荷率有利于电力系统的经济运行。负荷率定义为平均负荷与最大负荷的百分比，即

(10)

式中，Pl，av、Pl，max分别为负荷平均值与最大值。

负荷率变化量定义为电动汽车响应后与响应前的负荷率之差，即

ΔK=K′-K。

(11)

式中，K、K′分别为电动汽车响应前后的负荷率。ΔK越大，则说明协同调度对负荷率的改善效果越好。

3.1.2 峰谷差

峰谷差H的大小反映了电网所需要的调峰能力，峰谷差越小，越有利于电网运行的经济性。峰谷差H定义为最大负荷与最小负荷的差值，即

H=Pl，max-Pl，min。

(12)

峰谷差变化量定义为电动汽车响应前后电网净负荷峰谷差之差，即

ΔH=H-H′，

(13)

式中，H、H′分别为电动汽车响应前后的峰谷差。ΔH越大，则说明协同调度降低电网峰谷差的效果越好。

3.1.3 负荷波动率

负荷波动率[17]L的定义为负荷的标准差与负荷平均值之比，即

L=σ/Pl，av，

(14)

其中，

式中：σ为负荷标准差，反映了负荷功率的分散程度；pl，i为N点功率曲线中第i点的功率值。负荷波动率L能反映负荷分散程度的相对大小，L越小，说明负荷越平缓，越有利于电网的调度运行。

波动率变化量定义为电动汽车响应前后净负荷波动率之差，即

ΔL=L-L′，

(16)

式中，L、L′分别为电动汽车响应前后的波动率。ΔL越大，则说明协同调度平抑净负荷波动的效果越好。

3.2 电动汽车协同调度效果的衡量指标

本文采用电动汽车互动潜力、电动汽车与可再生能源出力耦合度、峰谷差变化比这3个指标评价电动汽车参与协同调度的程度和效果。

3.2.1 电动汽车互动潜力

Seepage calculation and discussion of double drainage blind ditch in finite thickness aquifer YE Kun WANG Xian-neng(68)

电动汽车互动潜力I描述电动汽车参与互动后功率增加或减少的最大值，用于表征电动汽车参与互动的能力，其定义为电动汽车参与互动后的最大功率改变量与相应时段其无序充电时功率的比值，即

(17)

式中：ΔPe，max为互动后电动汽车充电负荷最大功率变化值；Pe，0为对应时段无序充电状态下的功率值。电动汽车互动潜力I越大，说明电动汽车可参与协同调度的容量越大，其应对可再生能源波动的能力就越强。

3.2.2 耦合度

如果电动汽车充电能与可再生能源发电特性相配合，即电动汽车充电功率曲线与可再生能源发电功率曲线如果相似，将会有助于消纳可再生能源，平抑可再生能源带来的功率波动，提高电力系统运行的经济性。本文采用电动汽车充电负荷曲线与光伏出力曲线的相关系数，构造电动汽车充电负荷与光伏出力耦合程度指标C。通过对比电动汽车协同调度前后耦合度的变化，可以得知电动汽车可消纳新能源出力潜力的变化情况。

电动汽车充电功率与光伏发电的耦合度定义为

(18)

3.2.3 峰谷差变化比

(19)

D如果为正值，其值越大，则说明电动汽车与可再生能源协同调度的削峰填谷作用越明显。

4 仿真分析

4.1 算例说明

为了验证本文所提出的电动汽车-光伏发电协同调度模型的有效性，并分析应用该模型对电网负荷特性的改善效果，采用天津市某区域的数据作为算例，进行仿真实验。算例中，采用该区域2017年夏季典型日的48个测试点实际负荷曲线作为模型中的基础负荷曲线，即Pl。由于实际数据中电动汽车充电功率和光伏发电功率的数值较小，若直接使用实际的电动汽车充电功率和光伏发电功率代入模型进行计算，则协同调度后电网的负荷特性变化不明显，无法真实反映本文所提协同调度模型的效果。对此，将实际的电动汽车充电功率曲线和光伏发电功率曲线乘以一定的系数，使它们与负荷曲线的比值为某一比例，并将该比例称为渗透率。这样，就可以获得一定渗透率下的电动汽车充电功率和光伏发电功率曲线，分别作为模型中的Pev、Ppv。算例中该地区的电动汽车种类复杂，难以对电池剩余电量、充电功率等参数进行准确设置，在仿真时假设各时段电动汽车剩余电量均已满足约束，以便于计算。由于本文仿真中的Pev采用已知实际数据，因此，这样的假设具有合理性。模型的约束条件为式(4)、(5)、(8)和(9)。

根据天津市该区域电动汽车的增长趋势，未来该区域电动汽车充电功率峰值预计可达到电网总功率的20%左右，因此，本文中电动汽车的渗透率设置为20%。当前天津市可再生能源发电规模不断扩大，该市“十三五”规划中提出，到2020年可再生能源发电量占全社会用电量的10%，预计该市局部地区可再生能源占比可达30%左右。因此，本文将光伏发电的渗透率分别设为10%、20%、30%，并研究在这3种光伏发电渗透率下应用本文所提电动汽车-光伏发电协同调度的影响和效果。

4.2 仿真结果与分析

应用上述模型进行仿真试验，式(8)中电动汽车有序充电功率裕度ηmax和ηmin分别设置为0.1和1.2。采用MATLAB调用Yalmip工具箱的方法求解该模型，得到电动汽车渗透率，为20%、光伏发电渗透率分别为10%、20%、30%下的电动汽车与光伏发电协同调度的结果，如图4～6所示。

图4 光伏渗透率为10%时协同调度结果Fig.4 Result of cooperative dispatching with PV penetration of 10%

图5 光伏渗透率为20%的协同调度结果Fig.5 Result of cooperative dispatching with PV penetration of 20%

以图4为例进行分析。图4中，原净负荷曲线即为电动汽车无序充电时的净负荷曲线，由原始负荷曲线Pl减去渗透率为10%的光伏发电功率曲线得到。可看出原净负荷曲线的谷值出现在8:00附近，峰值出现在18:00附近，且在光伏发电接入的时间段(8:00—18:00)，该部分的负荷曲线有较大波动。而相比于原净负荷曲线，电动汽车有序充电后的净负荷曲线的谷值有所提高(对应图3中8:00附近的负荷)，而峰值有所下降(对应图3中18:00附近时刻的负荷)。可见，通过本文所提模型的协同调度，可减少净负荷的峰谷差。

图6 光伏渗透率为30%的协同调度结果Fig.6 Result of cooperative dispatching with PV penetration of 30%

对比图4中电动汽车有序充电和无序充电功率曲线可发现，在夜间净负荷功率较低的时间段(如1:00—7:00)，电动汽车有序充电功率略高于其无序充电时的功率，而在净负荷较大的时间段(如10:00—16:00)，电动汽车有序充电功率略低于其无序充电时的功率，这说明本文所提的协同调度模型能引导电动汽车在夜间电网负荷较低时多充电，而在负荷高峰时少充电，实现削峰填谷。

图5、图6分别为光伏渗透率为20%和30%时的电动汽车与光伏发电协同调度结果。由图5～6可看到与图4相似的现象：电动汽车有序充电后得到的净负荷曲线相比于原净负荷曲线，曲线的峰值下降而谷值上移。说明在光伏渗透率为10%、20%、30%的情况下，应用本文所提出的协同调度模型均能达到削峰填谷的效果。

为定量分析该电动汽车-光伏协同调度模型对电网负荷特性的影响，计算不同光伏渗透率下协同调度后电网的特性指标，结果如表1所示。

表1 电网净负荷特性指标Tab.1 Net load characteristic index of grid

由表1可看出，当光伏渗透率分别为10%、20%、30%时，电动汽车有序充电情况下电网的负荷率均高于无序充电时的负荷率，而峰谷差和波动率均比无序充电情况下的低。这说明在不同光伏渗透率下，应用该电动汽车-光伏协同调度模型均可以提高电网的负荷率，降低峰谷差，并减少净负荷的波动性。且随着光伏渗透率的提高，负荷率、峰谷差和波动率的变化量在增大。这意味着光伏并网的渗透率越高，该模型调度电动汽车进行削峰填谷、平抑波动的作用就越强，其改善负荷特性的效果就越明显。

由表2可看出，在电动汽车渗透率一定的情况下，随着光伏渗透率的提高，净负荷峰谷差变化比增大，电动汽车有序充电功率与光伏发电功率的耦合度也越高。这说明光伏接入电网的比例越高，本文所提出的电动汽车与光伏协同调度模型的削峰填谷作用越明显，电动汽车充电功率与可再生能源发电的耦合性越强，越有利于消纳可再生能源、抑制净负荷波动。同时可看到，在有序充电后电动汽车充电功率与光伏发电功率的耦合度并没有大幅度提高。这是因为该地区的电动汽车无序充电与光伏出力已经具有较强的耦合度，在运用本文模型对算例进行优化后，二者耦合度提升的空间有限。

表2 电动汽车协同调度效果的衡量指标Tab.2 Indicators for cooperative dispatching of electric vehicles %

5 结 论

本文以电网净负荷方差最小为目标函数，建立了电动汽车有序充电与光伏发电协同调度的模型，并提出定量分析协同调度后电网和电动汽车负荷特性的指标。通过天津市某区域电网的历史负荷数据进行算例仿真，验证了模型的有效性。研究结果表明，在不同的光伏渗透率下，本文所提出的电动汽车有序充电机制均能够平抑光伏发电的随机性对电网净负荷带来的波动，提高负荷率，降低负荷的峰谷差。