核电站冷却剂平均温度系统的模糊PI并行控制研究

王 科, 潘瑾宜

(1.江苏元洲生物工程有限公司, 江苏 镇江 212000; 2.上海电力大学, 上海 200090)

PI控制是根据偏差负反馈来调节参数的经典控制方案,优点是算法简单,有较好的稳定性和可靠性,已被广泛应用于一些过程控制中。传统核电站的冷却剂平均温度控制系统也采用PI控制策略,当负荷需求与堆芯功率不匹配时,冷却剂平均温度测量信号与设定值将产生温度偏差,温度偏差信号反映了当前的功率失配情况,由此会产生相应的控制棒(R棒)控制信号,实现对冷却剂平均温度的调节。这个控制过程体现了PI控制的基本思想。

文献[1]在负荷阶跃变化时对核电机组的冷却剂平均温度控制系统进行了仿真,以观测冷却剂平均温度系统的调节性能;文献[2]在核电站甩负荷状况下进行了冷却剂平均温度系统的模拟;文献[3]对大型压水堆负荷跟踪模式下冷却剂平均温度的变化进行了仿真。以上文献的仿真结果表明,PI控制下的系统具有一定的自调节能力,但调节效果有待改善。PI控制器参数的整定常常采用人工整定的方法,而实际的工业生产过程往往具有非线性以及时变性,PI控制难以对其产生理想的控制效果。另外,上述文献考虑的均是控制棒棒位输入信号下对系统的影响,将控制棒的动作当作瞬时完成的,而从实际工程角度来说,忽略了控制棒自身的延迟性。

为了研究针对控制棒棒速的冷却剂平均温度控制器,提升控制效果,达到节省能源、控制发电成本的目的,本文将冷却剂平均温度差值的大小作为模糊控制与PI控制切换的条件,融合PI控制的控制精度高以及模糊控制能较快提升控制速度的优点,实现模糊PI并行控制。依据秦山二期核电站的运行参数以及相关动力学方程搭建冷却剂平均温度被控系统,并且将模糊PI并行控制实验结果与传统PI控制实验结果进行对比,用以验证模糊PI并行控制的控制效果。

1 冷却剂平均温度被控系统模型的建立

1.1 中子物理学模型

反应堆堆芯通过中子裂变反应产生能量,所以首先需要建立系统的中子物理学模型,用以表示反应性与堆芯热功率的关系。根据单群扩散理论,将整个堆芯当作点堆模型,那么考虑6组缓发中子的点堆动态方程组[4]为

(1)

式中:P——堆芯热功率;

ρ——反应性;

βi——第i组缓发中子有效份额;

λi——第i组缓发中子衰变常数;

Ci——先驱核衰变功率;

l——中子代时间。

1.2 堆芯热力学模型

堆芯化学反应产生的热量需要传递给二回路,以便二回路蒸汽发生器工作。根据堆芯到冷却剂的3个传热过程:燃料芯块与包壳之间的热传导过程、元件壁面与冷却剂之间的对流传热过程以及利用冷却剂将堆芯热量传到堆外的输热过程,建立起对应这3个传热过程的机理模型[4]:

(2)

式中:c1——单位长度燃料芯块比热容;

Tf——燃料平均温度;

Tcd——包壳平均温度;

R1——芯块与包壳之间的等效热阻;

rf——燃料芯块半径;

qv——燃料的体积释热率;

c2——单位长度包壳比热容;

Tm——冷却剂平均温度;

R2——包壳与冷却剂之间的等效热阻;

cpm——冷却剂比热容;

M——堆芯冷却剂装量;

F——燃料元件释热比;

h——对流换热系数;

Acs——总传热面积;

Tin,Tout——冷却剂入口和出口温度;

1.3 温度反馈模型

核反应堆的反馈作用极其复杂,与热工水力以及堆芯物理特性和结构特点相关。本文考虑其中主要的两种反馈:燃料温度负反馈和冷却剂温度负反馈。当核反应堆的功率发生变化时,燃料温度也随之发生改变。当燃料温度发生变化时,促使冷却剂温度变化,但因为冷却剂热容量较大,所以燃料温度负反馈效应有一定的延迟。温度反馈模型[4]为

[ρf(t-1)+αfΔTf]+ρm(t-1)+

αmΔTm

(3)

式中:ρrod——控制棒反应性;

Rs——R棒棒速;

ρI——R棒组的微分价值;

ρf——燃料温度反馈反应性;

αf——燃料温度反馈系数;

ΔTf——燃料平均温度变化量;

ρm——冷却剂温度反馈反应性;

αm——冷却剂温度反应性系数;

ΔTm——冷却剂温度变化量。

1.4 冷却剂平均温度系统模型

秦山二期核电站是装机容量为2台600 MW的压水堆核电机组[5]。秦山二期核电站的主要堆芯参数如表1所示。

表1 秦山二期核电站堆芯参数

由于压水堆是一个复杂的工程系统,在仿真过程中忽略一些非线性因素的影响,将其余参数取工程整定值,例如,燃料温度反馈系数取-1.0×10-5,冷却剂温度反馈系数取-8.0×10-5,控制棒微分价值取3.5 pcm/步。将相关参数代入式(1)～式(3)中,得到冷却剂平均温度被控系统模型。冷却剂平均温度被控系统整体结构如图1所示。

图1 冷却剂平均温度被控系统模型

图1表示了输入为棒速Rs和系统输出为冷却剂平均温度Tm的被控系统结构图。由图1可知,系统具有较强的非线性,结构也相对较为复杂。

2 模糊PI并行控制器

2.1 模糊控制

模糊控制是基于模糊推理,模仿人类思维的一种现代智能控制方法,具有较强的鲁棒性,能够解决一部分无法建立起精确数学模型的控制问题[6],为非线性、干扰性较强的工业制造过程提供具有优良效果的控制策略。模糊控制一般分为以下几个流程:确定控制量与观测量;确定输入隶属度函数;确定输出隶属度函数;建立规则库以及反模糊化处理[7-8]。

本文取控制量为Rs,观测量为ΔTm。当冷却剂平均温度小于设定值时,控制棒需要向上提升使反应性增大;当冷却剂平均温度大于设定值时,控制棒需要向下插入使反应性减小,从而使冷却剂平均温度实时跟踪设定值变化。为了扩大模糊控制的适应范围,将控制量与观测量进行标准化变换。本文将Rs标准化变换到[-1,+1]区间,将ΔTm标准化变换到[-3,+3]区间。处理方式为

(4)

将控制量以及观测量的模糊子集均划分为负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB)5个。在MATLAB工具箱内有一些常用的隶属度函数,如三角形隶属度函数、梯形隶属度函数、高斯型隶属度函数以及z型隶属度函数和s型隶属度函数等。若隶属度函数较为尖锐,则其分辨率较高;若隶属度函数较为平缓,则分辨率较低[9]。本文利用MATLAB仿真平台搭建一维模糊控制的隶属度曲线。经过论域变换后的ΔTm在相应模糊子集中的隶属度函数如图2所示。Rs在相应模糊子集中的隶属度函数如图3所示。

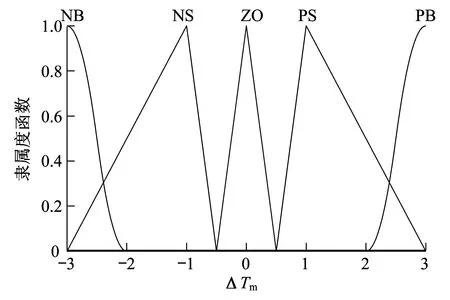
图2 ΔTm隶属度函数

图3 Rs隶属度函数

模糊规则库的建立由一系列语言表达式构成,常用的有IF-THEN语句、ALSO语句和AND语句等。这些语句需要利用相应的模糊推理机制进行数值化,才能得到模糊矢量。本文采用IF-THEN语句制定模糊规则表,如表2所示。

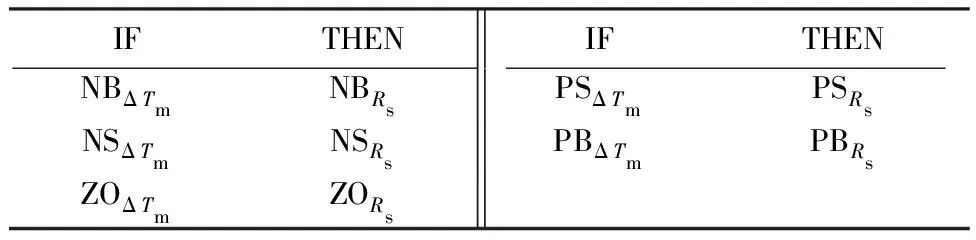
表2 模糊规则

常用的反模糊化方法有最大隶属度平均法、面积重心法、面积等分发等。本文采用常用的最大隶属度平均法进行反模糊化处理,由模糊矢量求解得到控制棒棒速输入量。

若仅利用模糊控制对冷却剂平均温度进行控制,则依照上述规则选取模糊控制相关参数。冷却剂平均温度模糊控制系统结构如图4所示。

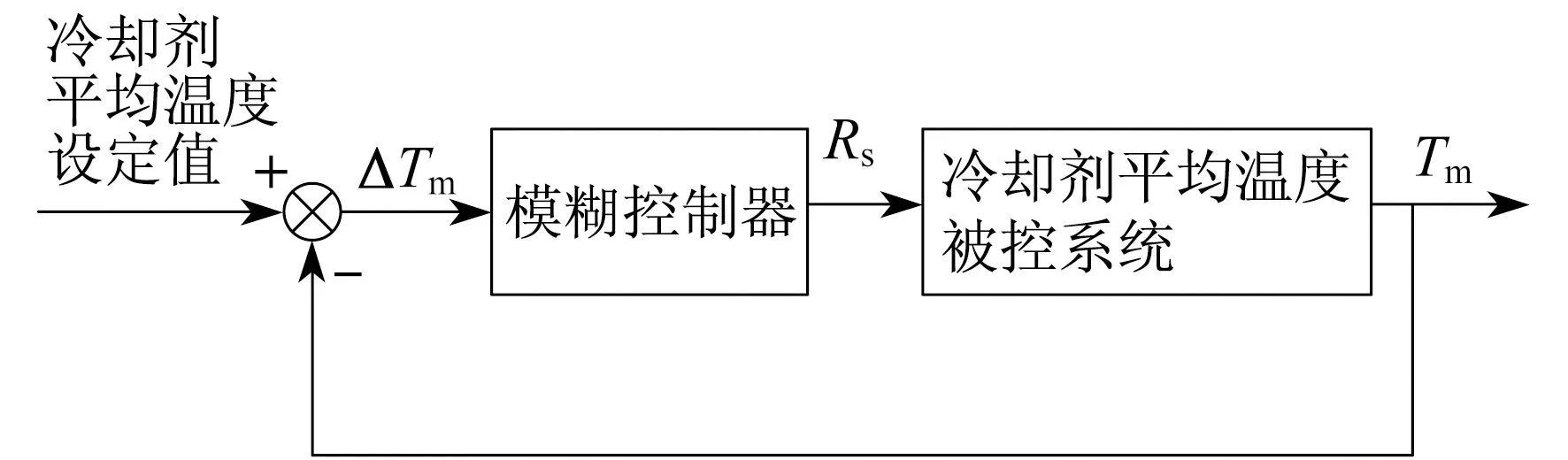
图4 冷却剂平均温度模糊控制系统结构

2.2 模糊PI并行控制

模糊控制虽然能够较好地提升非线性复杂系统的控制速度,但是其很难在被控量接近设定值时进行精准控制。为了解决这一矛盾,利用PI控制对控制系统的精度进行弥补,设计模糊PI并行控制器,经过多次仿真试验后,确定了一个ΔTm相对合适的切换范围。当冷却剂平均温度设定值与实时值之差达到-0.06～0.06 ℃时切换为PI控制,而ΔTm的值不处于此范围时切换为模糊控制。其中,PI控制参数分别取kp=1.2,ki=0.6。冷却剂平均温度模糊PI并行控制系统结构如图5所示。

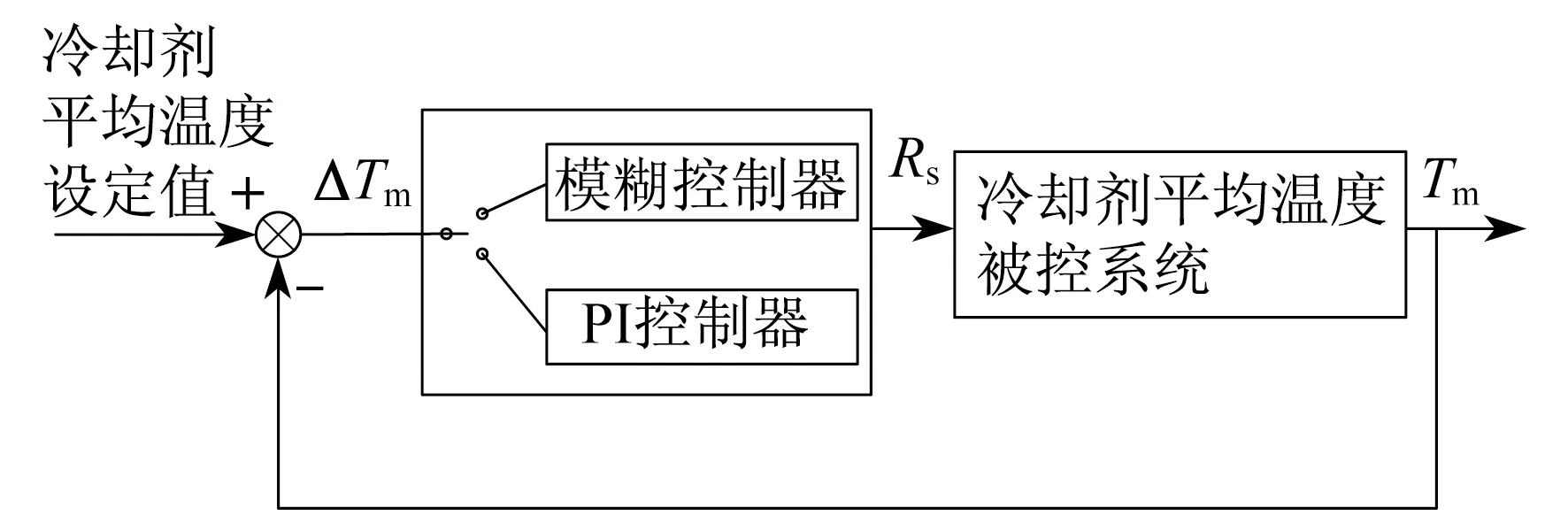
图5 冷却剂平均温度模糊PI并行控制系统结构

3 MATLAB仿真结果

满功率工况下,冷却剂平均温度值为306.9 ℃。为了检测控制器对冷却剂平均温度的调节能力,在0～250 s给定309.9 ℃的阶跃信号,250～520 s给定308.4 ℃的阶跃信号,作为冷却剂平均温度的设定值。

基于MATLAB仿真平台,分别搭建冷却剂平均温度模糊控制系统以及模糊PI并行控制系统,进行冷却剂平均温度的实时控制。模糊控制器的控制效果如图6所示。

图6 模糊控制器的控制效果

由图6可知,模糊控制器对冷却剂平均温度的调节过程效果不是特别理想,调节时间较长,但在0～250 s的上升速度和250～500 s的下降速度比较快,上升时间为60 s左右,下降时间为50 s左右。因此,为了弥补模糊控制在被调量接近设定值时控制精度不高的问题,利用图5所示的模糊PI并行控制对模糊控制器进行改良。

将由模糊并行控制器与两组PI控制器的控制效果进行对比。第1组PI控制器的控制参数取kp=0.14,ki=0.1;第2组PI控制器的控制参数取kp=0.28,ki=0.22,仿真结果如图7所示。

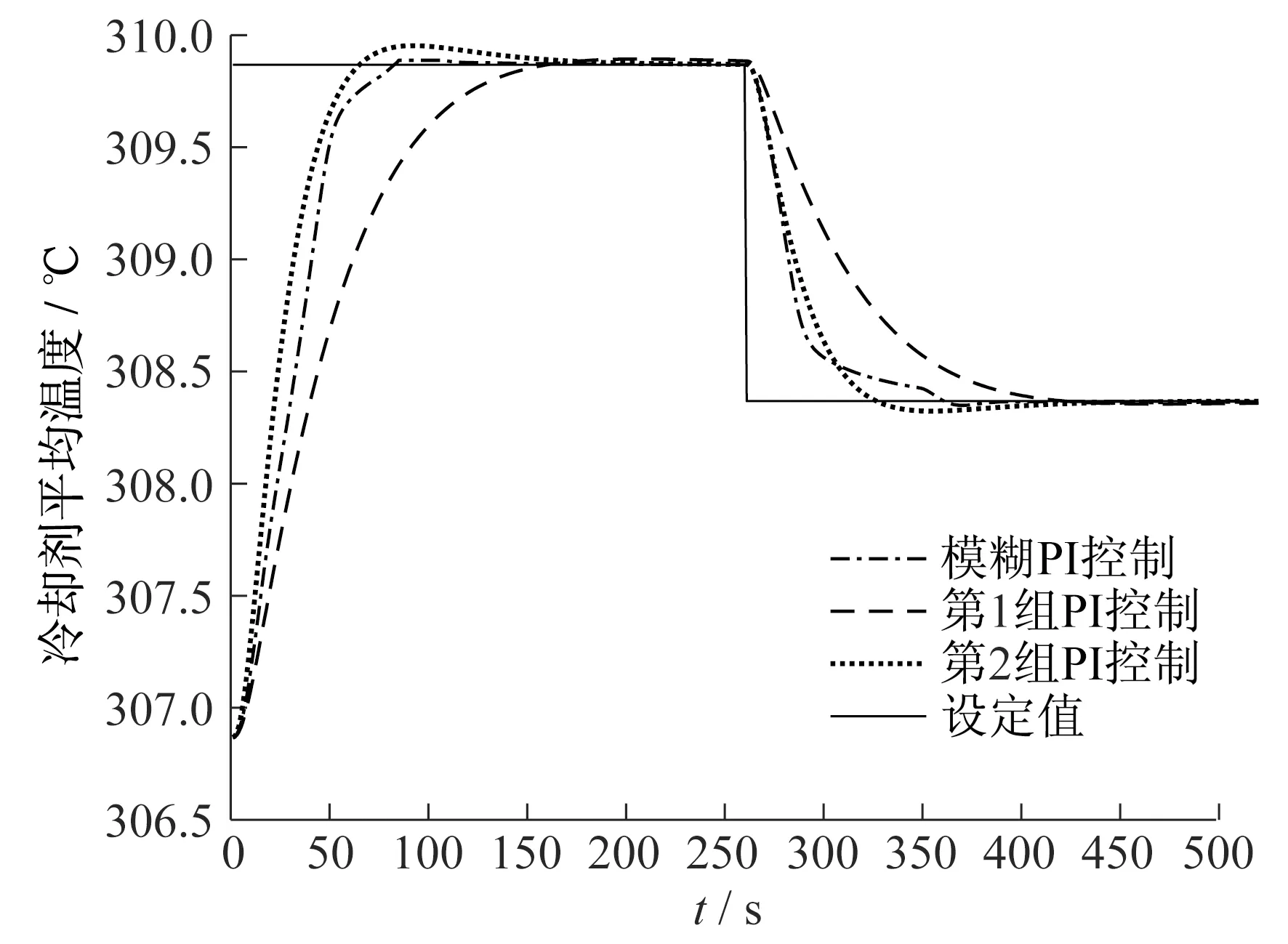
图7 模糊PI并行控制器与两组PI控制器效果对比

由图7可知,在第1组PI控制器作用下,0～250 s控制期间的上升时间为120 s,250～500 s控制期间的下降时间为105 s。在模糊PI并行控制器作用下,0～250 s控制期间的上升时间为60 s,250～500 s控制期间的下降时间为50 s。由动态特性参数的对比可知,模糊PI控制的调节时间更短。在第2组PI控制器作用下,系统上升时间、下降时间与模糊PI控制相同,但具有一定的超调,在0～250 s控制期间超调量为3%,250～500 s控制期间超调量为2.4%;而模糊PI并行控制下系统无超调。综合上升时间、下降时间以及超调量等系统动态性能指标表明,模糊PI并行控制下冷却剂平均温度系统具有更好的调节性能。

4 结 语

本文根据秦山二期核电站相关数据搭建了冷却剂平均温度MATLAB控制系统模型,建立了基于控制棒棒速输入下的冷却剂平均温度被控系统。利用冷却剂平均温度与设定值的差值大小进行模糊控制与PI控制并行切换的方法,弥补了模糊控制以及传统PI控制的缺陷。与传统PI控制效果的仿真对比表明:在相同的冷却剂平均温度设定值下,模糊PI并行控制与模糊控制相比精度更高,与PI控制相比系统超调量更小,调节速度更快;模糊PI并行控制在冷却剂平均温度的调节速度和精度上均有较大提升,验证了该控制器具有良好的控制性能。