（五年级）怎么做能更好地探索和理解等式的性质

□蓝海鹏

小学生处于算术思维阶段，探索和理解等式的性质是由算术思维到代数思维转换的重要过程，以等式的基本性质为例，教师在教学中可采用如下教学环节。

一、操作探索，感知算理

教师呈现图片：1个天平，8个砝码（5g、50g、100g各1个，20g共2个，10g共3个），2瓶饮料（重量均为xg）。请学生思考：要使天平平衡，你有哪些放置方法？能用图示、文字或算式表示吗？学生独立操作时教师巡视并收集典型作品。

二、借图探索，探明算理

1.理解“天平平衡”的内涵。教师呈现图1至图4，提问：它们平衡吗？看天平图你能写出哪些算式？

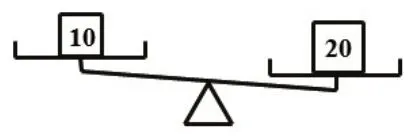
图1

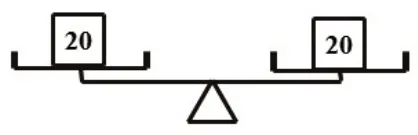
图2

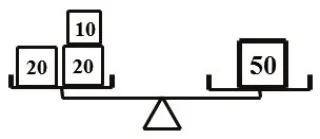
图3

图4

结合屏幕上的天平图，引导学生思考什么情况下天平会平衡或者不平衡，帮助他们逐步明晰要使“天平平衡”，需要“左右两边物体质量相等”。

2.理解“不平衡到平衡”的本质。教师请学生思考并操作：①如图2，在左托盘添加1个10g的砝码，右托盘（），天平才能保持平衡？②如图3，从左托盘取走1个10g（或1个20g）的砝码，要使天平平衡，右托盘应该怎样放？③如图4，在左右托盘各添加1个砝码，要保持天平平衡，你会怎样做？

以上问题，你能画图并用算式表示吗？让学生逐步体会到平衡的天平两边“同时加上（或减去）”同一个量，天平仍然保持平衡。

三、借式探索，深化算理

教师出示任务：观察图5至图9，在括号中任意填一个数或字母，使得等式或不等式成立。归纳：等式两边同时加上（）的数或字母，等式仍然成立。

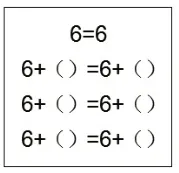
图5

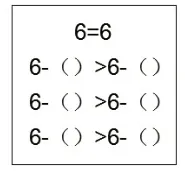
图6

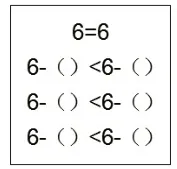
图7

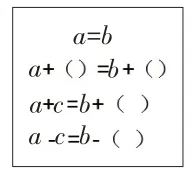
图8

图9

四、模型探索，解释算理

教师请学生根据“如果a=a，则a-2=a-2（a为任意数或字母）”编一道应用题。学生独立编题，或根据教师提供的模型材料编题。

（1）质量模型：形如上述天平。

（2）数目模型：①甲乙两队进行拔河比赛，各有9人，如果甲队减少2人，要使游戏公平，乙队也要减少2人。②分物游戏等。

（3）面积模型：如图10。

（4）体积模型：如图11。

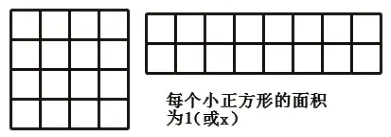
图10

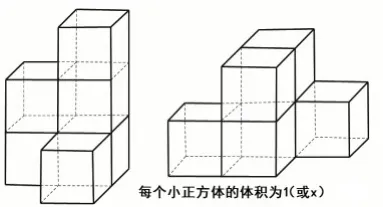
图11

以上教学过程，学生借助操作，用图示、算式和文字等方式表征、归纳性质，不仅提高了数学知识探索能力，而且有效地发展了数学建模思想。