非饱和土力学行为的三维离散元分析

周凤玺 ， 赵 曼， 应 赛

(1. 兰州理工大学土木工程学院， 甘肃 兰州 730050； 2. 西部土木工程防灾减灾教育部工程研究中心， 甘肃 兰州 730050； 3. 兰州理工大学技术工程学院， 甘肃 兰州 730050； 4. 长江师范学院土木建筑工程学院， 重庆 408100)

0 引言

非饱和土在自然界中广泛存在， 尤其是在干旱与半干旱地区. 由于受气候条件的影响， 存在着若干种具有特殊性质的土类， 如膨胀土、 黄土与残积土等特殊土， 它们均具有非饱和土的基本特性. 在工程实践中， 如在路堤及土坝工程的建设过程中， 通常涉及到膨胀土、 湿陷性土的变形分析以及边坡稳定与滑坡等问题. 但由于土体通常处于非饱和状态， 孔隙水和孔隙气共存， 使得非饱和土的力学特性与饱和土相比较显得非常复杂. 以往大都通过室内直剪试验与三轴试验， 来获得非饱和土的强度参数以及应力-应变曲线等宏观力学性质， 或通过离散单元法， 从细观角度分析土颗粒的运动规律以及孔隙水的作用力. 其中， 三轴剪切试验的优点在于可以控制围压， 应力状态、 应变测量方便可靠， 能够反映试样受力变形直到破坏的全过程， 但是， 室内三轴剪切试验成本高、 制样复杂， 技术要求高， 且耗时长. 相比之下， 三维离散元数值模拟不仅能通过控制颗粒级配、 孔隙率等生成数值试样， 通过借助标定细观参数的方式考虑含水率、 剪切强度等因素， 还具备成本低、 效率高、 易建模等明显的优势.

离散单元法是从细观尺度分析颗粒材料力学性质以及解决非连续介质力学问题的数值计算方法. 自从Cundall等[1-2]提出离散单元法后， 利用离散单元法对土体力学的研究已经取得一系列成果[3-7]. Liu等[8]通过离散单元法对非饱和土在各向同性压缩和双轴剪切过程中的破坏机理进行数值模拟， 确定颗粒间不同毛细黏聚力下的屈服应力； Jiang等[9]应用二维离散元法研究非饱和土的抗剪强度并提出两个能够考虑大吸力范围和颗粒级配影响的抗剪强度函数； 蒋明镜等[10]应用三维离散元法， 考虑毛细水的作用， 研究吸力对密实和松散颗粒材料强度的影响； 在此基础上， 许自立[11]通过三维离散元法建立非饱和土三轴剪切试验和单轴拉伸试验的离散元计算模型， 研究非饱和土的强度问题.

在非饱和土离散元数值模拟的过程中， 大多采用颗粒流软件PFC中内嵌的线性平行黏结模型或线性接触黏结模型来模拟土中的基质吸力， 这两种模型适用于模拟黏结材料的力学行为. 但是， 在程序运行的过程中， 需要人工不断地调节黏结参数来近似模拟土中的吸力， 其本身不符合实际中非饱和土的基质吸力. 对于蒋明镜等[9-10]所提出的毛细水模型， 是将毛细水作用考虑入颗粒间作用力， 在PFC3D中编写fish语句， 每当有新的颗粒接触时， 将新产生的接触模型变为毛细水模型. 然而， 对于这种用户自定义的接触模型， 需要基于第三方编译平台编写准确且符合实际的程序代码， 其技术难度高， 且耗时长、 难推广.

本文基于颗粒流理论， 借助离散元数值模拟工具PFC， 综合考虑非饱和土的孔隙水压力、 含水率等因素， 基于Hill接触模型， 建立非饱和土的颗粒流模型， 并从细观角度深入分析非饱和土的力学特性， 旨在对利用数值方法高效解决非饱和土强度相关问题进行探索.

1 离散元模型

1.1 Hill材料

Hill材料被定义为颗粒集合体， 且Hill接触模型存在于所有的颗粒-颗粒间接触处， 所组成的Hill材料类似于不饱和的颗粒材料. 首先， Hill接触模型可能只存在于颗粒-颗粒间的接触处， 可将水分添加到Hill材料中， 如果水分状态是湿的， 则颗粒间存在液桥， 如果水分状态干燥， 则不存在液桥. 其次， Hill接触模型提供了一个微小的、 非线性弹性(无张力)和摩擦界面， 具有压缩表面相互作用力的行为， 并可携带吸力， 故采用Hill接触模型来考虑湿颗粒材料.

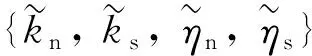
Hill模型是在液桥模型的启发下建立的， 这种模型机械地捕捉颗粒间分散的液体对颗粒系统宏观响应的影响. 只有当水分状态为湿时， 才会出现吸力Fm， 这是一种在法线方向的吸引力. 当颗粒接触时最大， 并且呈指数形式衰减， 直到接触间隙达到一个临界值2scr时， 液桥破裂， 此时水分消失吸力减小为零. 在不饱和的颗粒材料中， 考虑到与表面张力有关的吸力， 即在颗粒间接触处保持孔隙水的作用， 从而考虑了水分效应在Hill材料中的作用. 通过以下方法可在选定的颗粒之间加入吸力来模拟Hill材料中的水分. 每个Hill接触都有水分状态， 可以是湿的， 也可以是干的， 当颗粒-颗粒间产生新的接触时， 被指定为干的Hill接触模型， 在模拟的过程中， 通过调用函数@him_makeWet(ψ,gm)， 可以将水分随时加入到Hill材料中， 其中ψ为吸力，gm为粒间距离. 在此函数被调用后， 具有吸力的Hill接触模型将存在于彼此的粒间距离内的所有颗粒之间.

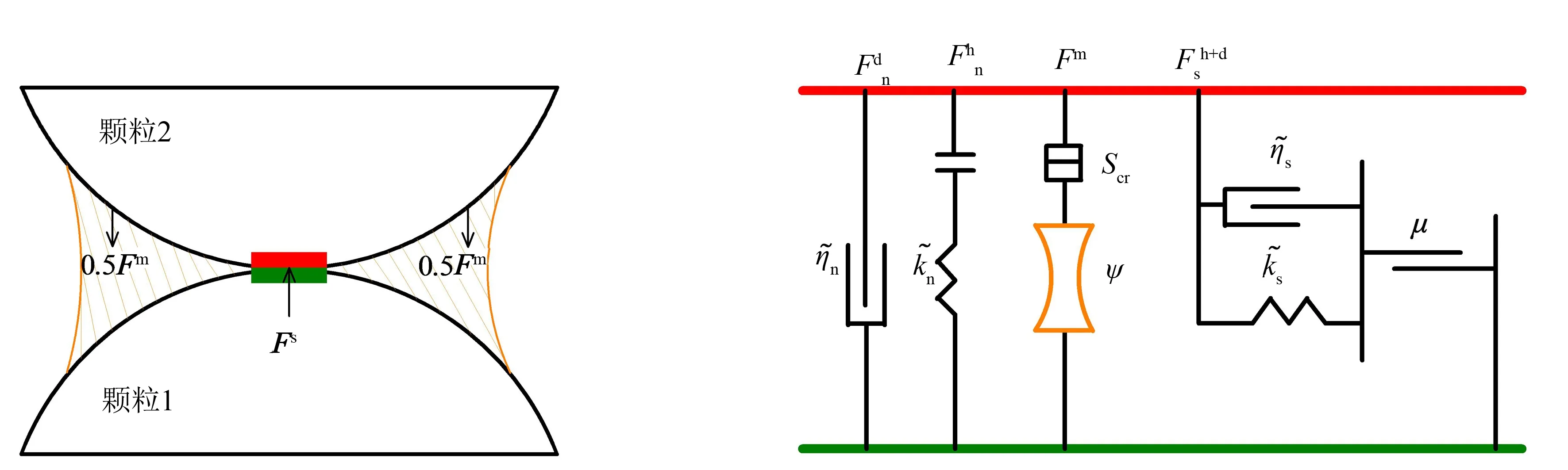
(a)颗粒-颗粒接触示意图 (b)Hill’s法向和切向方向流变接触模型图1 湿的Hill接触模型的力学行为和流变特性Fig.1 Behavior and rheological components of the wet hill contact model

1.2 力-位移定律

Hill接触模型的力-位移定律：

Fc=Fs+Fm;Mc≡0

(1)

式中：Fs为颗粒间的表面相互作用力；Fm为吸力. 表面相互作用力由赫兹力和阻尼力组成：

Fs=Fh+Fd

(2)

另外， 表面相互作用力Fs可分解为法向力和切向力：

(3)

吸力作用在法线方向：

Fm=-Fmnc

(4)

式中：Fm>0为张力(吸力)且Fm≥0.

2 非饱和土室内三轴剪切试验的离散元模拟

2.1原型试样颗粒级配

本文使用的试验数据来自室内非饱和重塑黄土三轴剪切试验[12]， 该试验采用FYS30型应力-应变控制式非饱和三轴仪， 进行非饱和黄土等吸力三轴剪切试验. 试验中选用新疆西部伊犁地区重塑黄土， 天然含水量为4%～16.1%， 主要以粉土为主(含量高达81.5%)， 含有少量的砂粒(0.5%)和黏粒(18%)， 其基本物理性质见表1.

表1 伊犁黄土试样基本物理性质

2.2 离散元模型

建立三轴剪切试验的颗粒流模型可分为试样生成、 预固结和竖向加载3个阶段. 以室内非饱和土重塑黄土三轴剪切试验为基础， 进行离散元模拟. 模型边界由圆柱筒和上下两面墙体组成， 墙体尺寸与室内试验中所制备的土样大小相一致， 直径39.1 mm， 高80 mm， 土粒相对密度为2.72. 由于试样尺寸与颗粒粒径相差较大， 直接生成颗粒工作量大、 计算时间过长， 且生成模型不够直观， 因此考虑对颗粒粒径进行适当比例放大， 当模型最短边长度为颗粒平均粒径的30倍以上时， 可忽略尺寸效应[13]. 本文离散元试样颗粒级配如图2所示， 颗粒粒径在0.6～6.0 mm之间， 颗粒总数在5 000～8 000之间.

通过伺服机制， 以迫使模型接近真实的物理过程， 即通过对模型边界条件的调整， 使得颗粒体系间的接触尽可能快地达到理想状态， 然后在其基础上进行加载分析， 完成模型试样的预固结过程. 在PFC3D中， 由于墙体在其接触处是允许发生一定重叠的刚体， 故减小侧面墙体的刚度来模拟橡皮膜的柔性边界， 墙体刚度取试样颗粒刚度的1/10[14]. 在数值模拟的过程中， 颗粒与墙体之间通过接触发生作用， 设颗粒与墙体间的摩擦系数为零， 采用线性接触模型， 颗粒与颗粒间采用Hill接触模型. 对于每一个颗粒， 都能满足运动定律， 由于刚性墙体没有质量， 因此墙体受到的不平衡力无法影响墙体的运动， 即墙体不符合运动定律， 不能直接施加外力， 只能施加速度， 在PFC三轴剪切试验中， 通过对墙体施加速度来达到相应的围压. 非饱和土三维离散元试样数值模型如图3所示.

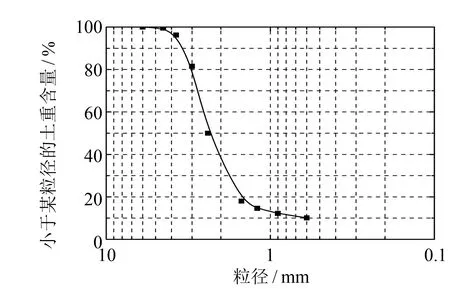
图2 离散元试样颗粒级配曲线Fig.2 Particle size distribution of numerical sample

图3 非饱和土三维离散元试样数值模型Fig.3 Numerical model of three-dimensional discrete element specimen of unsaturated soil

剪切阶段中， 墙体内部上、中、下分别设置半径为19.55 mm的测量圆， 记录并监控不同时步下模型内部应力、 应变、 孔隙率以及配位数等变化过程. 此外， 控制侧面墙体的围压恒定， 对固结后的模型试样在垂直方向上施加竖向应力. 此时上下墙体按恒定的速率对模型试样进行加载， 使得试样在周围压力和竖向应力共同作用下产生竖向和径向变形， 从而获取模型试样的应力-应变关系曲线. 当竖向应力出现峰值或轴向应变达到15%时， 则认为试样已经发生破坏[15].

2.3 模型参数标定

图4给出干密度ρd=1.39 g·cm-3， 饱和度Sr=60%的试样， 在相同吸力不同围压下应力-应变曲线的离散元数值结果， 并与室内三轴剪切试验结果进行比较. 从图4可看出， 数值模拟结果与室内试验实测曲线较为吻合， 可模拟非饱和土的三轴剪切试验. 离散元分析中的材料参数如表2所示.

(a) 吸力与黏聚力的关系

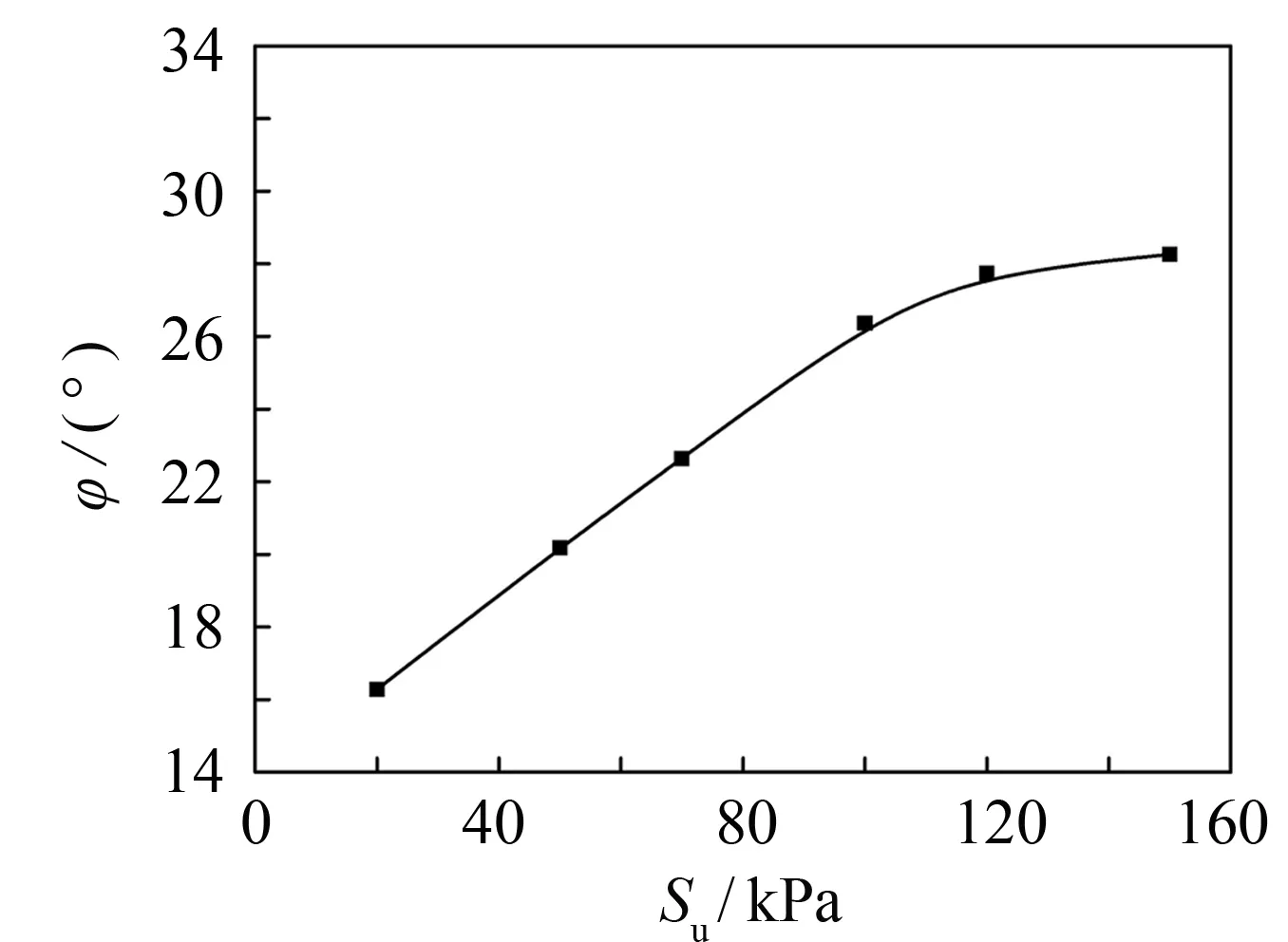
(b)吸力与内摩擦角的关系

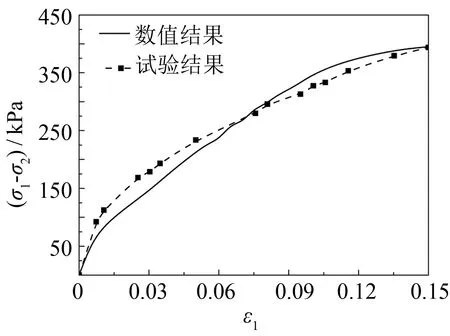
(c) Su=70 kPa， σ3=300 kPa

PFC模型中的细观参数与宏观参数之间具有高度非线性的关系， 且相互之间具有一定耦合性， 即使只调整一个细观参数也可能会同时影响到多个宏观特性. 因此， 细观参数的标定顺序至关重要. 对于Hill接触模型， 首先， 确定模型所处的围压和吸力的大小； 其次标定杨氏模量和泊松比， 二者是通过控制颗粒法向和切向刚度的大小， 进而影响曲线的斜率； 最后， 对摩擦系数进行标定， 控制曲线峰值高度. 另外， 局部阻尼系数根据工程实践经验所得取常数值0.7[16]， 其他值与室内试验各参数相对应. 此时三轴剪切试验数值模型所表现出的宏观特性， 将与相应的室内试验结果接近或基本吻合， 再根据宏细观参数之间相互影响的一般规律， 对细观参数做进一步调整， 即可快速标定出数值模型细观参数.

表2 离散元试样细观参数标定结果

3 非饱和土离散元分析

3.1 应力-应变关系曲线

对于干密度ρd=1.39 g·cm-3， 饱和度Sr=60%的试样， 在吸力Su=70 kPa和各级围压(100， 200和300 kPa)下， 按恒定的加载速率进行竖向压缩， 通过调节模型参数， 得到同密度、 同吸力， 不同围压下的应力-应变曲线. 在此基础上， 改变吸力的大小， 根据应力-应变曲线的变化规律， 分别研究围压和吸力对非饱和土抗剪强度的影响.

图5(a)所示为ρd=1.39 g·cm-3的试样在吸力Su=70 kPa时不同围压下的应力与应变关系， 该试样呈应变软化特性. 当围压σ3=100 kPa时， 最大主应力差值在100 kPa附近， 当围压σ3=200 kPa时， 最大主应力差值在250 kPa附近， 当围压σ3=300 kPa时， 最大主应力差值在400 kPa附近， 说明围压对试样的影响较为明显. 试样达到相同轴向应变时， 围压σ3=300 kPa的情况下施加的竖向应力大于围压为200 kPa下施加的竖向应力; 同样， 围压σ3=200 kPa下施加的竖向应力大于围压为100 kPa下的情况， 即增大围压有利于提高土样的强度. 对比图5(a)～(d)， 当吸力从70 kPa逐步增加到200 kPa， 试样的应力-应变曲线由应变软化向应变硬化发展， 说明增大吸力可以改变应力-应变特性.

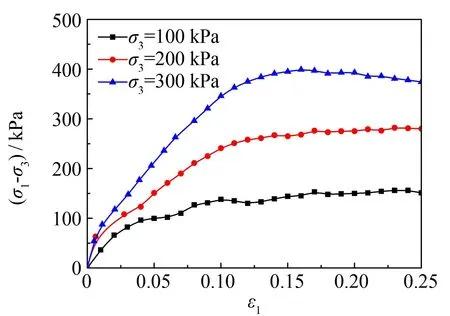
(a) Su=70 kPa， ρd=1.39 g·cm-3

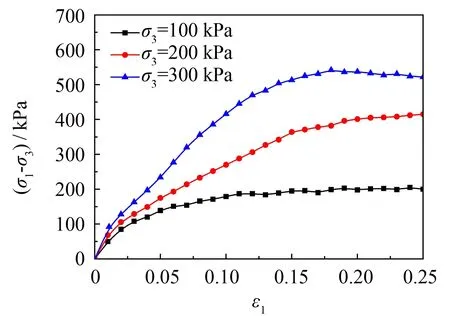
(b) Su=100 kPa， ρd=1.39 g·cm-3

(d) Su=200 kPa， ρd=1.39 g·cm-3

3.2 强度特性

根据密度ρd=1.39 g·cm-3的试样， 在吸力Su=20、 50、 70、 100、 120和150 kPa下的应力-应变曲线， 利用莫尔-库伦强度理论， 获得不同吸力下试样的抗剪强度包线， 从而得到非饱和土模型试样的抗剪强度参数， 如图6所示. 同一密度的试样， 随着吸力的增加， 其黏聚力和内摩擦角均呈非线性增加， 在高吸力段， 黏聚力增加的速度大于低吸力段， 此外， 随着吸力的增大， 内摩擦角增加速度放缓.

(a) 吸力与黏聚力的关系

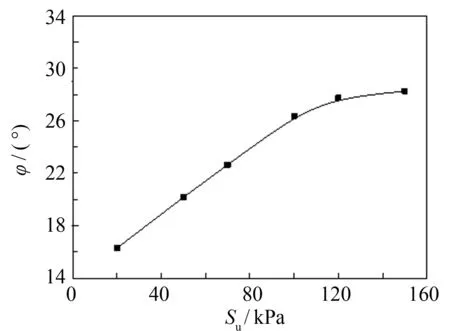
(b) 吸力与内摩擦角的关系

3.3 吸力与含水率的关系

以干密度ρd=1.39 g·cm-3， 饱和度Sr=60%的离散元试样， 在吸力Su=70 kPa、 围压σ3=200 kPa的条件下所得的应力-应变曲线为基础， 结合室内试验中非饱和土试样在相同密度不同饱和度下的应力-应变曲线， 对离散元试样的吸力值进行调整， 标定饱和度为40%和20%时的应力-应变曲线， 从而获得不同饱和度下离散元试样的应力-应变关系曲线， 如图7所示.

由数值模拟所得的离散元试样在不同饱和度下的吸力值， 可绘制出Hill接触模型下吸力与含水率的关系曲线， 如图8所示. 在7%～21%的变化范围内， 含水率随吸力的增大呈线性递减.

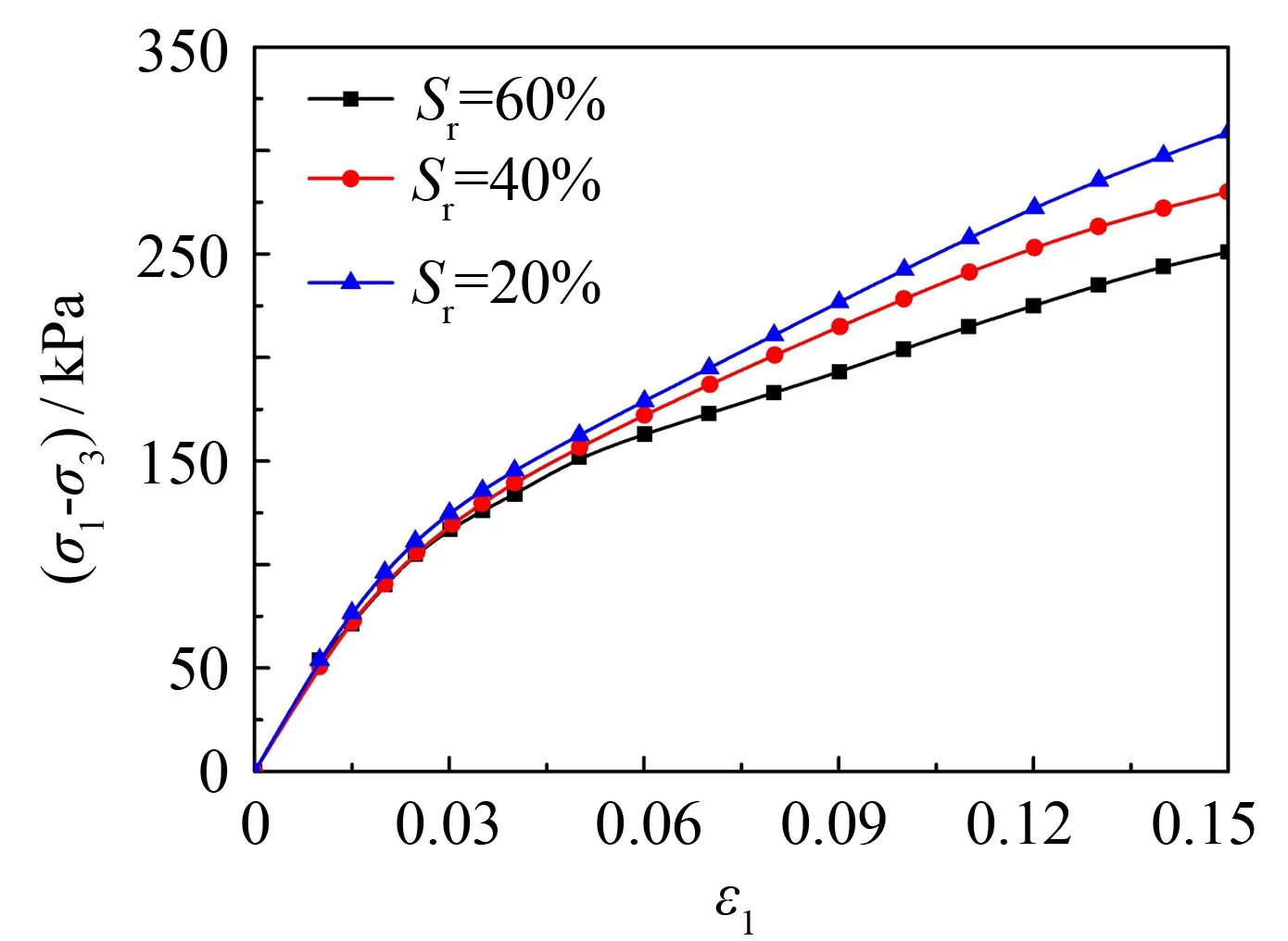
图7 不同饱和度下离散元试样的应力-应变关系曲线Fig.7 Stress-strain curves of discrete element specimens under different saturation

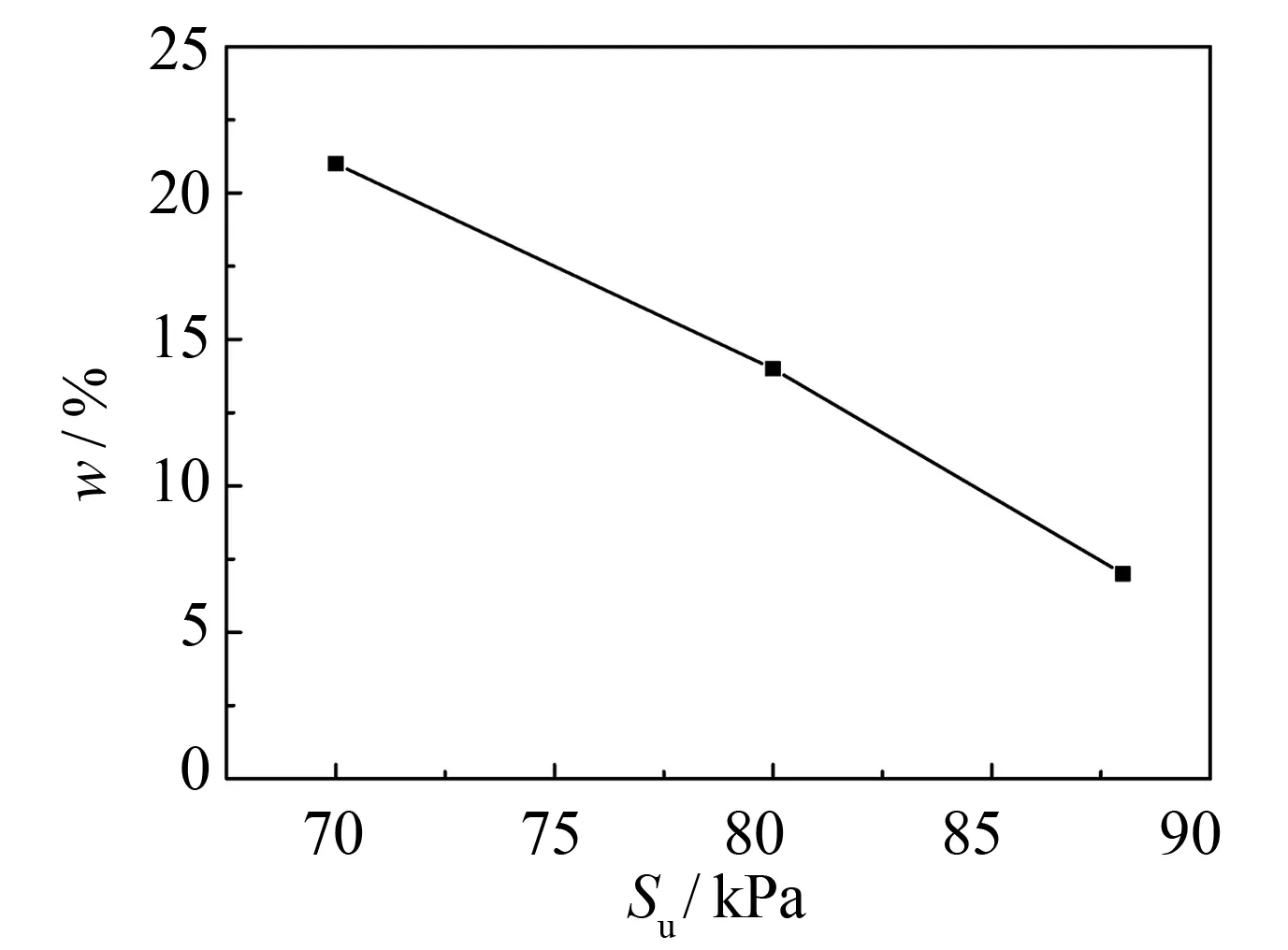
图8 吸力与含水率的关系曲线Fig.8 Relationship between suction and water conten

4 结语

1) 在剪切过程中其抗剪强度随围压和吸力的增大显著提高， 且随着吸力的增大， 应力-应变曲线由应变软化向应变硬化发展.

2) 黏聚力和内摩擦角均随吸力的增大呈非线性增加， 低吸力段黏聚力增加速度缓于高吸力段， 且随吸力的增大内摩擦角增大速度变缓.

3) 随着模型试样含水率的减小， 吸力线性增大， 应用Hill接触模型的颗粒流模型可以较好模拟非饱和土的力学行为.