基于Trefftz法的沿海越流含水层系统地下水研究
杨鹭茜, 苏 燕, 顾承宇
(1. 福州大学土木工程学院, 福建 福州 350108; 2. 台湾海洋大学工学院, 台湾 基隆 20224)
0 引言
Trefftz法是快速求解边界值问题最常用的边界无网格法之一, 其应用越来越广泛, 近似解可表示为满足控制方程函数的线性组合[1]. 根据Kita和Kamiya的研究, Trefftz法分为直接法和间接法[2]. Kita等[3]描述Trefftz法在求解三维Poisson方程中的应用, 使用笛卡尔坐标系中的多项式函数来近似含有未知函数的不均匀项, 从而确定泊松方程的解. Trefftz法在工程中的应用主要有Laplace方程、 双谐波方程和二维边界检测问题[4-5]. Li等[6-7]对Trefftz法、 配点法和其他边界方法进行全面比较, 总结出Trefftz法是求解方程最简便的计算方法, 该法提供最精确的方程解和最佳的数值稳定性. 为了获得线性方程组的精确解, Liu[8-11]对 Trefftz法做出改进, 将单个特征长度合并到T型完整基底中, 使得到的线性方程组的条件数明显减少. 除单尺度Trefftz法外, Ku等[12]基于标量同伦方法提出一般动力学法, 并证明求解线性代数方程组的数值稳定性, 尤其是对于病态问题系统, 可得到病态条件极大的线性方程组在三维 Laplace问题上的解. 当前针对沿海地区地下水的研究较少, 其演化规律对许多滨海工程具有重要影响. 沿海越流含水层系统的承压含水层为自由含水层所覆盖, 且在它们之间存在着垂直方向的弱透水层. Jiao等[13]提出一个解析解, 用于描述沿海越流含水层地下水受潮汐影响. Li等[14]依据线性Boussinesq方程提出另一个近似解析解, 用于研究沿海越流含水层地下水动态. Li等[15]将推导的解析解用于研究越流含水层的渗漏和储水系数对地下水位变化的影响, 并发现来自含水层的渗漏会对承压含水层的地下水位产生较大的影响.
由于Trefftz法最初是用于处理欧氏空间的边界值问题, 因此难以找到Trefftz法应用于求解与时间相关的问题. 本文用Trefftz法首次建立沿海越流含水层系统中承压地下水流的暂态模型, 在时空坐标系统的基础上, 假定时间为自变量, 时空坐标系中的初始条件和边界条件均可视为时空边界上的边界条件, 通过对满足部分边界配点控制方程的Trefftz基底进行迭加, 来逐步近似在时空坐标系中得到的数值解. 文中还运用该方法对一些问题进行验证, 包括数值解与解析解的比较和精度研究, 以及沿海地下水的数值模拟.
1 Trefftz法基础理论
1.1 Trefftz基底推导
在均质、 各向同性、 等厚的越流含水层系统中, 承压地下水控制方程如下:

(1)
式中:h为承压含水层总水头;x为距离;t为时间;T为导水系数;L为越流系数;S为储水系数.
为了求得上述控制方程的暂态解, 应用分离变量法做出以下假定
h(x,t)=X(x)K(t)
(2)
将式(2)代入式(1), 得

(3)
为了简单易行地推导, 首先引入以下形式

(4)
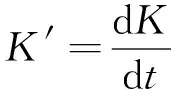
(5)
将式(4)与式(5)代入式(3), 得

(6)

为求得该方程的特征值, 采用常数p保证常数的正负. 分λ>0,λ=0,λ<0等3种情况.
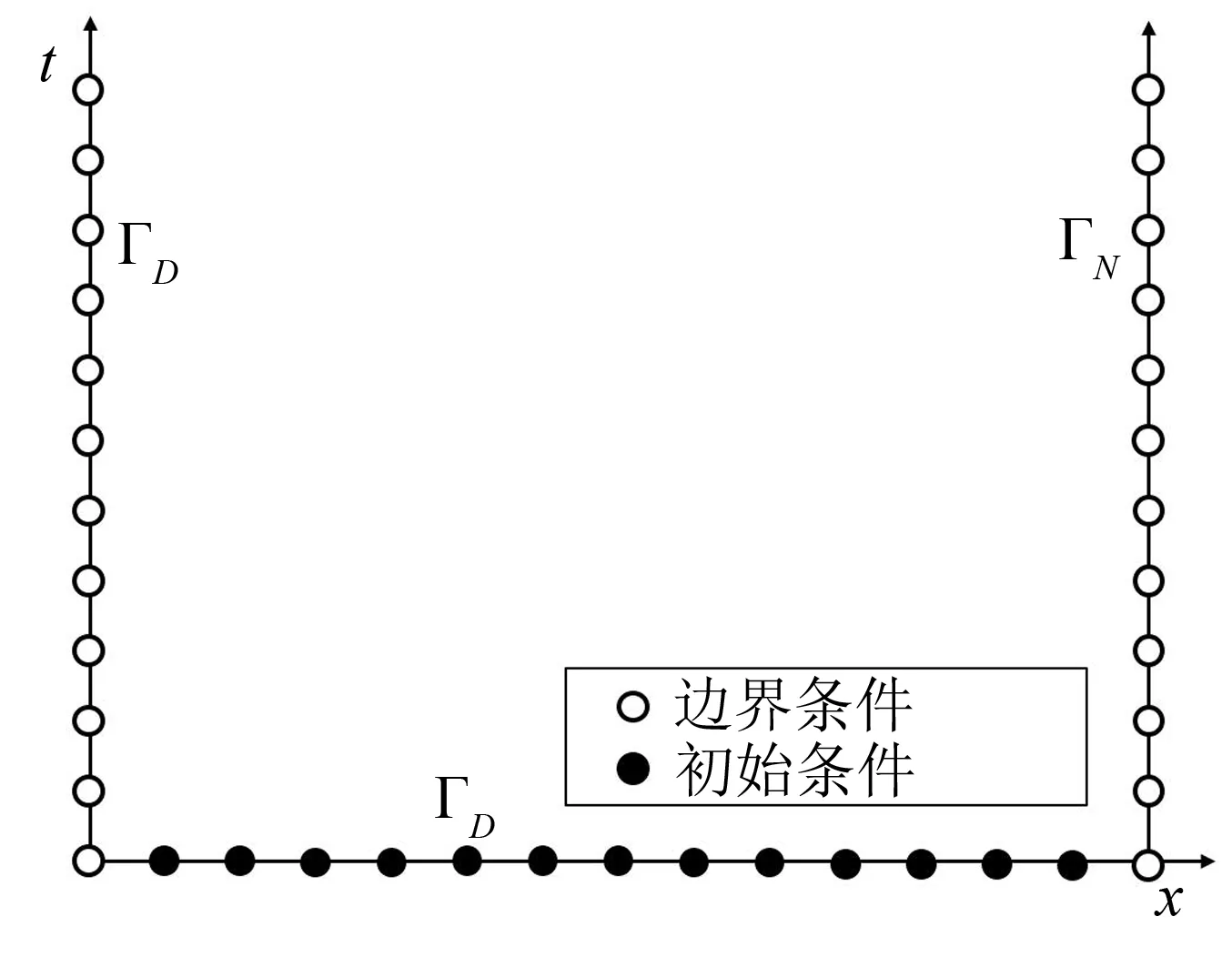
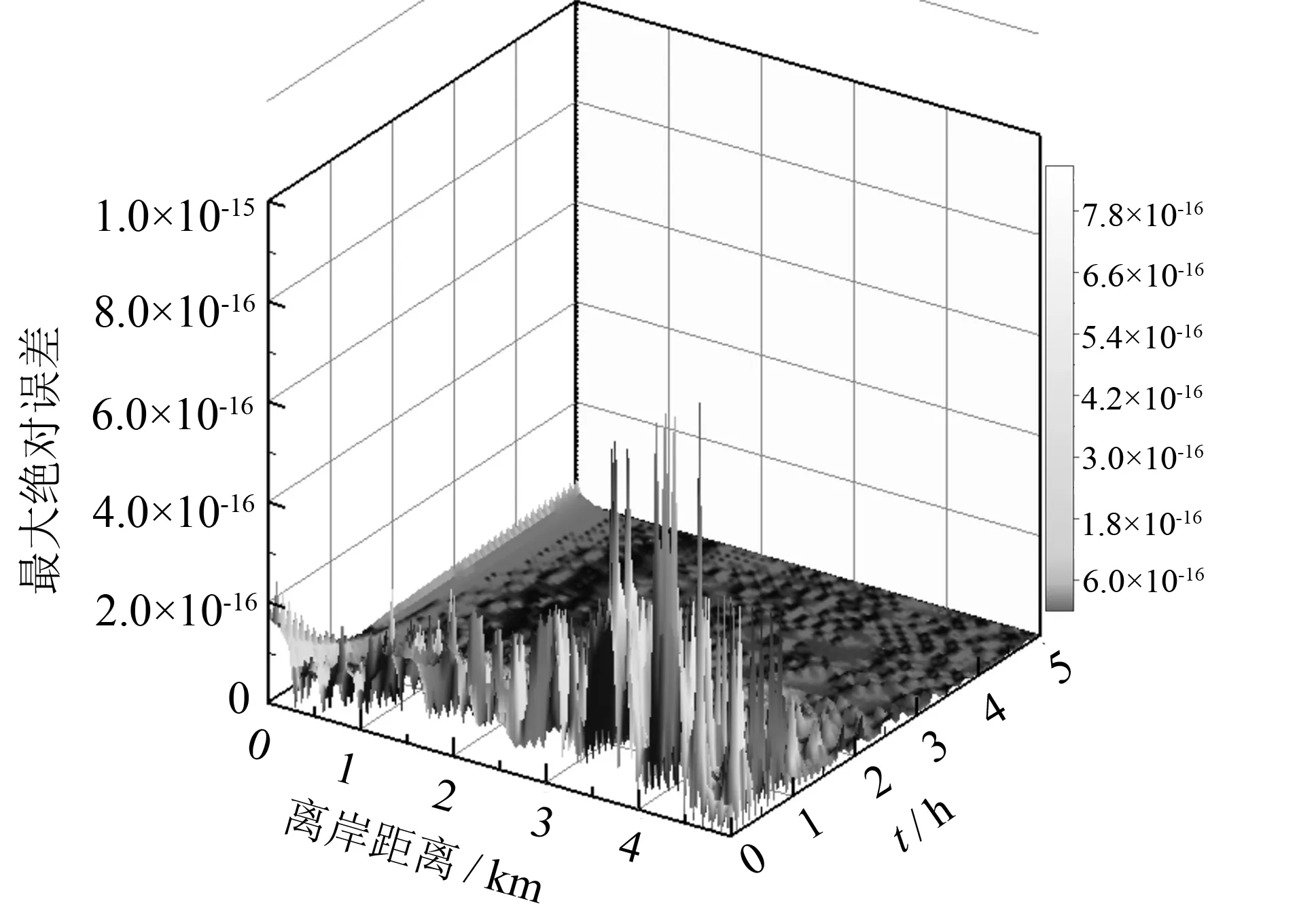
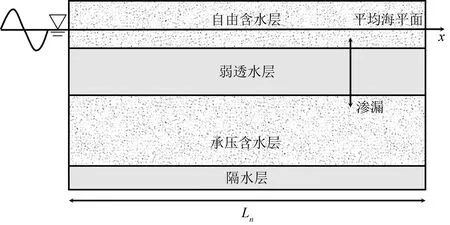
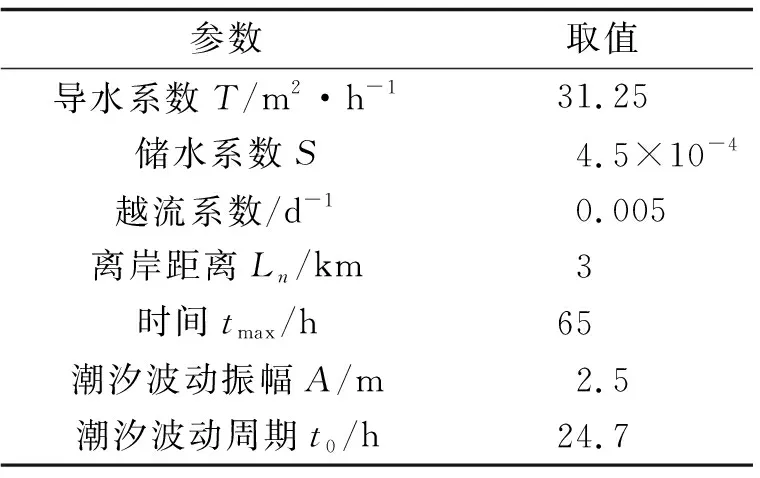
情况1λ>0, 即λ=p2(0 (7) 因此 X(x)=c1exp(px)+c2exp(-px) (8) (9) 将式(8)与式(9)代入式(2), 得 (10) K=d2 (11) 将式(9)与式(13)代入式(2), 得 (12) 式中:c1,c2,d1,d2,A1,A2,B1,B2为任意常数. 情况2λ=0 (13) 因此 X(x)=c3x+c4 (14) (15) 将式(14)与式(15)代入式(2), 得 (16) 式中:c3,c4,d3,A3,B3为任意常数. 情况3λ<0, 即λ=-p2(0 (17) 所以 X(x)=c5cos(px)+c6sin(px) (18) (19) 将式(18)与式(19)代入式(2), 得 (20) 式中:c5,c6,d4,d2,A4,B4为任意常数. 综上三种情况的分析, 利用加法定理对上述所有解进行迭加, 得到一个线性无关的沿海地下水控制方程的近似解 (21) 式中:A01,B01,A02,B02,A1p,B1p,A2p,B2p为任意常数;w为适用于控制方程近似解基底函数的阶数. 基于时空坐标系, 本文将时间定义为自变量, 采用时空坐标系对沿海地区地下水进行暂态建模. 本文建立的二维坐标系, 包括时间上的一维和空间上的一维, 以求解一维的沿海地区地下水问题, 时间和空间边界处的水头值均在研究域内的时空边界上给出, 从而使原始的一维问题转化为二维问题. 从越流含水层系统地下水控制方程式(1)开始, 边界条件与初始条件如下 图1 Trefftz法时空配点示意图Fig.1 Schematic diagram of Trefftz method with the space-time collocation method 式中:f(x,t)为给定的定水头边界条件函数;v(x, 0)为给定的初始条件函数; ΓD为定水头边界条件所在边界. 在时空坐标系统中, 将空间轴(x轴)的初始边界离散为n1点, 将时间轴(t轴)的边界离散为n2点, 如图1所示. 根据不同的边界条件, 分别将离散后的空间边界点代入给定的定水头边界条件函数f(x,t), 空间边界点代入给定的初始条件函数v(x, 0), 将计算出的边界值和初始值代入控制方程的近似解表达式(21), 并联立线性代数方程组, 以Aα=B的矩阵运算形式表示. (23) 式中: 矩阵A是由Trefftz基底所组成的尺度为aa×bb矩阵, 矩阵B是由边界值和初始值所组成的尺度为aa×1的矩阵, 待定系数α为尺度为bb×1的矩阵. 其中aa=2n1+n2,bb=4(w+1). 因为Trefftz基底本身满足沿海地区承压地下水控制方程, 所以只要时间轴的边界点和空间轴的初始边界点满足各自的边界条件, 通过Matlab左除运算, 由α=Α/Β即可求解待定系数. 将时空坐标系统内任意点代入Trefftz基底所构成的近似解中, 由Β=Αα即可计算出任意位置的水头值h(xi,tj). 本案例通过一维均质越流含水层地下水的模型, 以定水头作为边界条件进行数值验证, 说明了Trefftz法与时空坐标系统相结合求解一类边界条件下承压地下水问题的可行性. 研究区域表达式如下: Ω={(x,t)|0≤x≤Ln} (24) 下式是满足越流含水层地下水控制方程式(1)的解析解, 将其作为研究区域Ω的第一类边界条件与初始条件, 以验证数值模式. (25) 现设5 km的承压含水层的导水系数T=1.25 m2·h-1, 储水系数S=2×10-4, 越流系数L=0.005 d-1. 利用Trefftz法计算0~5 h内承压地下水位的变化过程, 并与解析解(25)进行比较, 得到二者的最大绝对误差. 其中, 数值验证的空间边界点n1与时间边界点n2均取51点,阶数为10阶. 图2显示了0~5 h范围内地下水问题数值解和解析解的变化情况, 从图2可看出, 数值解与解析解的变化趋势非常吻合, 有力地说明Trefftz法应用于研究越流含水层地下水的可行性. 在不同时间内, 承压地下水位与距离均呈现线性增长关系, 且随着时间的延长, 地下水位逐步降低至零, 达到稳定状态, 这符合实际地下水流动的演变规律. 为验证Trefftz法求解结果的准确性, 将数值解与解析解进行比较, 见图3, 结果表明, 二者的最大绝对误差8.90×10-16, 仅在初始时刻存在轻微的误差波动, 且随着时间和距离的增加, 其误差始终维持在10-16的高精度范围内, 未出现不收敛的现象. 图2 数值解与解析解的变化情况Fig.2 Change in numerical solution and analytical solution 图3 数值解与解析解的误差分析Fig.3 Error analysis of numerical solution and analytic solution 本案例假设某沿海地区越流含水层系统均质、 各向同性, 其自由含水层与承压含水层的地下水通过中部弱透水层在垂直方向发生渗漏[13]. 考虑到自由含水层的厚度远大于海洋潮汐波动的幅度, 合理地忽略自由含水层所受的潮汐波动的影响, 并假定其地下水位与平均海平面保持一致, 将平均海平面作为含水层系统的基准面, 选择x轴原点位于平均海平面和海滩的交界处, 向内陆延伸方向为正方向, 见图4. 图4 沿海越流含水层示意图Fig.4 Schematic diagram of coastal leakage aquifers 采用Trefftz法对该沿海越流含水层系统的承压地下水进行波动特性模拟测算, 并与有限差分的计算结果进行趋势拟合, 验证Trefftz法应用于沿海地下水模拟的准确性. 由越流含水层地下水控制方程式(1)出发, 将潮汐波动以正弦函数概化, 当含水层系统距离海岸足够远时, 地下水将逐渐趋于稳定, 直至与平均海平面一致, 整个含水层系统在时间t=0时刻的初始地下水位与平均海平面相同, 当t>0时, 自由含水层的地下水位依然保持恒定. 故潮汐边界条件、 内陆边界条件和初始边界条件表示如下 (26) 式中:A为潮汐波动振幅;t0为潮汐波动周期;Ln为越流含水层系统的离岸距离. 表1显示各项计算参数的取值情况, 该案例空间边界点n1离散为31点,每点间距100 m,时间边界点n2离散为66点,每点间隔1 h,阶数为25阶. 沿海地区含水层地下水初水位水平的情况如图5所示. 表1 沿海地下水模拟参数表 图5 Trefftz法与有限差分法地下水位波动曲线对比Fig.5 Comparison of groundwater level fluctuation curve between Trefftz method and finite difference method 图5中直观地反映了, 由Trefftz法计算得到的波动曲线与后项有限差分法计算得到的结果基本一致, 能够进行密切拟合, 在进一步证明Trefftz法于沿海地下水模拟研究适用的同时, 也直观地描述了沿海地区地下水位的波动特性. 由于受潮汐波动的影响, 不仅与潮汐具有相似的正弦函数波动特性, 始终在海平面附近上下波动, 还与潮汐波动具有相同的周期. 同时随着潮汐波不断向内陆传播, 近海水位变化比远岸水位变化更加明显, 直至离岸距离为1.5 km, 远岸水位的波动振幅已经逐渐稳定, 趋近于零. 1) 针对越流含水层系统中承压地下水建立模型, 无需使用传统的时间推算法就可以解决暂态问题. 通过数值验证表明, Trefftz法的数值结果不仅与解析解高度吻合, 而且能够产生极高精度的数值解, 从而证明该方法可便捷地应用于解决越流含水层系统地下水问题. 2) 沿海地区地下水的演化规律对许多滨海工程有着重要影响, 以越流含水层系统的概念模型为基础, 利用Trefftz法研究沿海地区越流含水层地下水的水位变化和波动, 并且和有限差分法的计算结果进行比较, 二者结果均反映了沿海地区地下水位随时间的波动和离岸距离的增大而逐渐衰减的高度拟合情况. 验证了Trefftz法应用于沿海越流含水层的可行性与高效性. 因此, Trefftz法的适用范围可能会在不久的将来扩展到沿海工程问题.
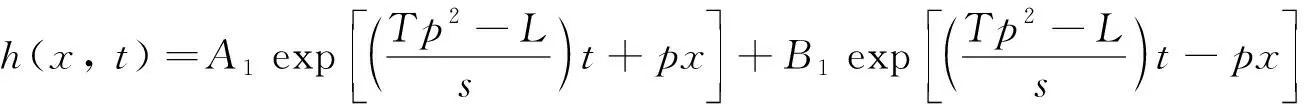

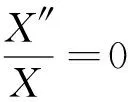
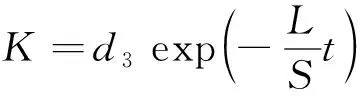

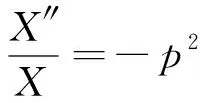
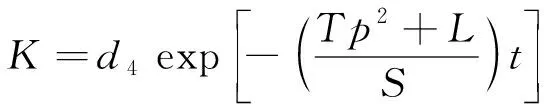

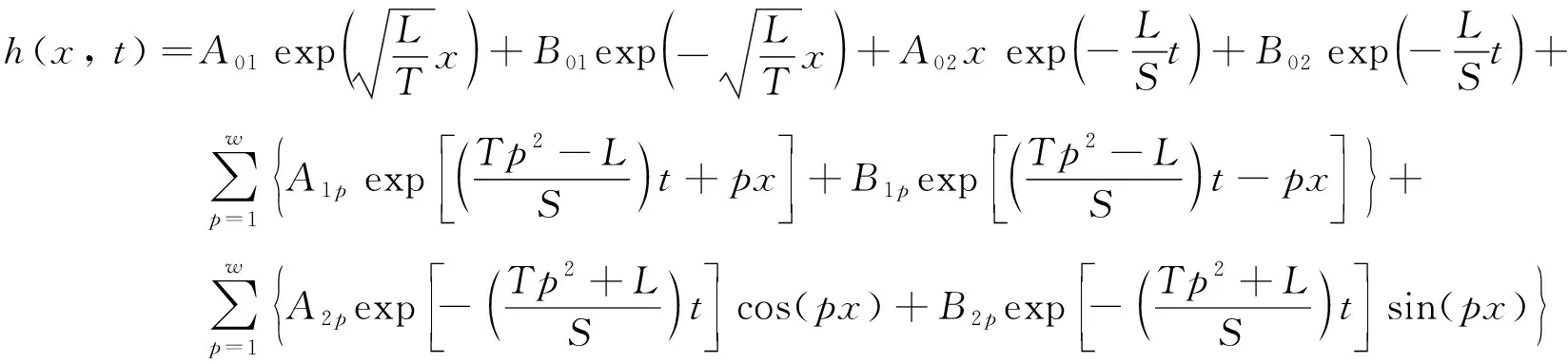
1.2 时空配点原理
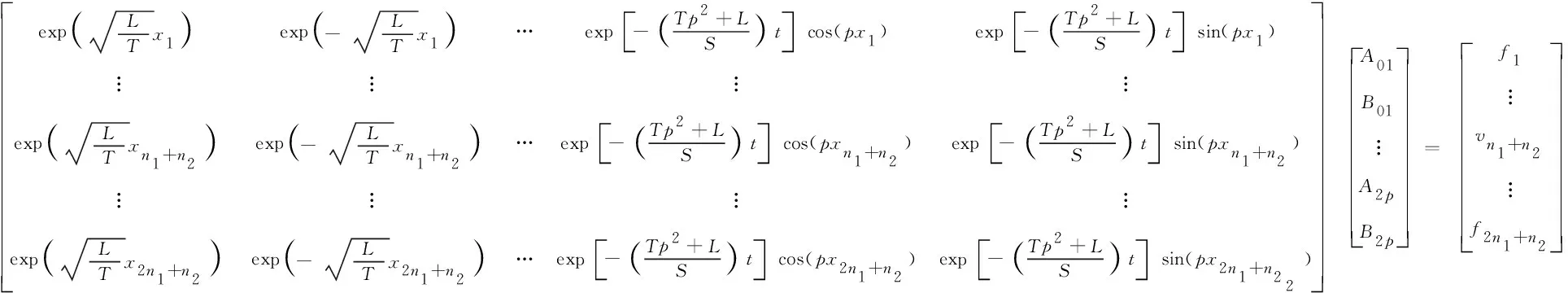
2 数值模拟分析
2.1 解析解数值验证


2.2 沿海地下水模拟
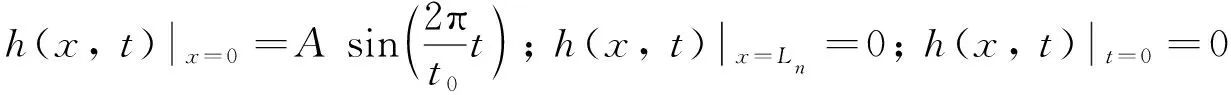

3 结语

