组基数约束指数跟踪问题的梯度投影算法

黄晓鑫, 吴景岚, 朱文兴*

( 1.福州大学 数学与计算机科学学院， 福建 福州 350116；2.闽江学院 计算机与控制工程学院， 福建 福州 350108 )

0 引言

如今, 基数约束优化的应用越来越多, 比如推荐系统、 压缩感知、 图像处理和计算机视觉等。 其目标是选择一部分的分量, 在满足基数约束的同时达到损失函数的最小值, 例如, 基数约束优化问题中的稀疏最小二乘回归问题：

其中A ∈Rm×n, 被广泛应用于压缩感知。 近些年, 基数约束投资组合优化问题因其广泛的应用面(如核密度学习[1]、 指数跟踪[2]、 投资组合再平衡[3]、 投资问题[4]等) 吸引了越来越多的关注, 该问题可以描述为：

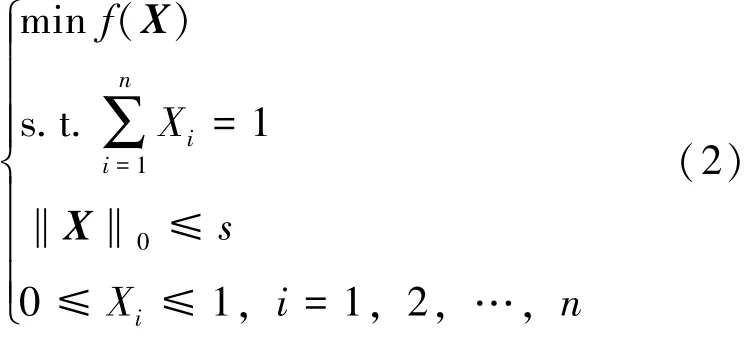
现有一些关于问题(2) 的算法, 比如梯度投影下降算法[5]、 非单调梯度投影算法[4,6]等。

基于先验知识, 可以把所有n 个分量分为N个不相交的大小相等的组, 每组有n0个元素,其中N 由具体场景确定。 本文中, 不失一般性,2, …, N 。 X 的组稀疏性可以通过l1,0范数来衡量, 其中：

当问题(1) 中的基数约束被换为组基数约束时, 有以下问题：

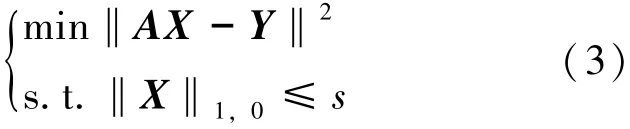
由于组基数约束优化问题不能直接描述投资组合优化问题, 且基数约束投资组合优化问题的算法不能求解组基数约束优化问题, 本文考虑如下组基数约束投资组合优化问题：

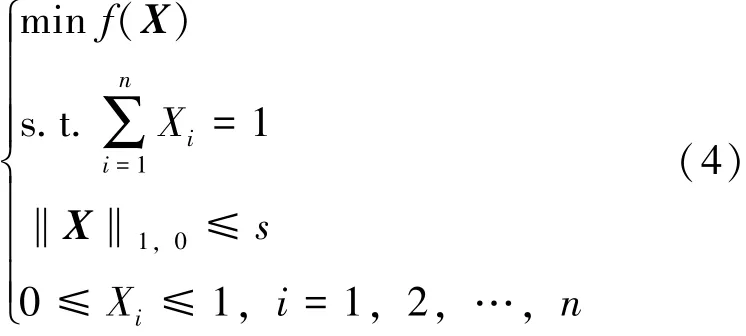
该问题结合了组基数约束优化问题和投资组合优化问题, 在金融和投资领域有现实意义, 如将产品分组, 并选择一些组进行投资等。

针对带组基数约束的指数跟踪问题(4),本文结合拉格朗日方法和梯度投影算法, 提出一种非单调迭代组软阈值算法, 而且证明了算法的收敛性。 实验表明算法性能较好。

1 拉格朗日方法

本文中, 范数‖⋅‖ 默认是欧氏范数。 假设函数f： Rn→R 的梯度是李普希茨连续的, 即存在Lf∈R, 使得对任意X, Y∈Rn有‖∇f(X) -∇f(Y)‖ ≤Lf‖X - Y‖。 且假设X ∈Rn存在不相交的组等分结构, 即X 的指标集{1, 2, …, n} 被分为不相交的大小相等的N 组, 分别是G1,G2, …, GN。 从而X = (XTG1, XTG2, …, XTGN)T,其中 XTGi= (Xj)Tj∈Gi= (XGi,1, XGi,2, …,XGi,n0)T, i = 1, 2, …, N。 这里XT表示向量X的转置。 用Xk来表示算法在第k 轮的迭代点。

记{X ∈R： ‖X‖1,0≤s, 0 ≤Xi≤1, i =1, 2, …, n} 为Ω, 则问题(4) 的拉格朗日对偶问题为：

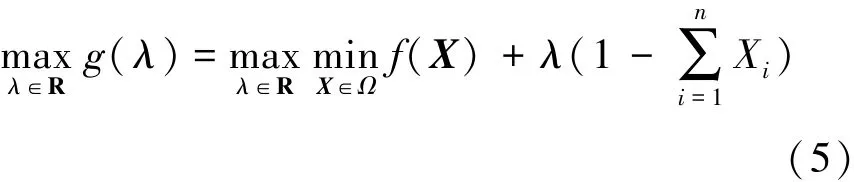
求解问题(5) 的内部问题等价于求解下面的问题(6)：

因为问题(6) 是NP 难的, 用f(X) 在当前解Xk处的二阶展开做近似, 即：

2 问题(7)的闭式解与迭代算法

首先, 对于给定的λ, 给出问题(7) 的最优解, 并证明其最优性。

证 对任意的X ∈Ω, 对任意的有且仅有s个元素的指标集B ⊆{1, 2, …, N}, 若X 的非零组指标集取B, 则有：

其中上述第二个不等式成立是基于Bk(λ) 的定义。 原因是这里要确定一个组指标集使得问题(7) 中的目标函数值最小, 而对于所有N 组中的第i 组, 若选中它, 则第i 组在问题(7) 中的目标函数值的最小值为选中第i 组比不选中第i 组, 问题(7) 中的目标函数值减少因此, 为了使问题(7) 中的目标函数值最小, 这里选择最大的s 个H(YkGi+的指标集。 在此基础上, 为了唯一确定指标集, 选指标最小的一个, 得到Bk(λ)。 进而从上述不等式及X 和B 的任意性可推出

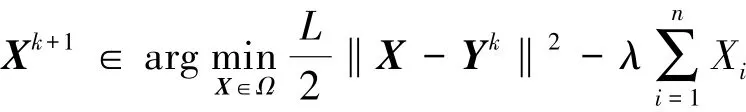
证毕。

根据定理1 给出的问题(7) 的最优解, 给出下面的组软阈值(Group Soft Thresholding,GST) 算法1, 用于求解问题(6)。

算法1X*←GST(L, λ, X0)

输入： L(L ＞Lf), λ, X0；

输出： X*；

1： 初始化： k ←0；

2： 重复

3： Xk+1←Γλ(Xk)；

4： k ←k + 1；

5： 直到满足终止条件；

6： X*←Xk。

下面给出算法1 的收敛性证明。

定理2令η = L - Lf, {Xk} 为算法1 产生的序列, 则有：

(1) 序列{Fλ(Xk)} 是单调不增的, 且以下不等式成立

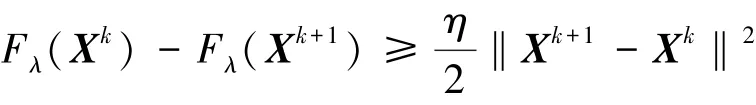
(2) 序列{Xk} 是收敛的。

证 因为∇f(X) 是李普希茨连续的, 所以有：

又L ＞Lf, 则有：

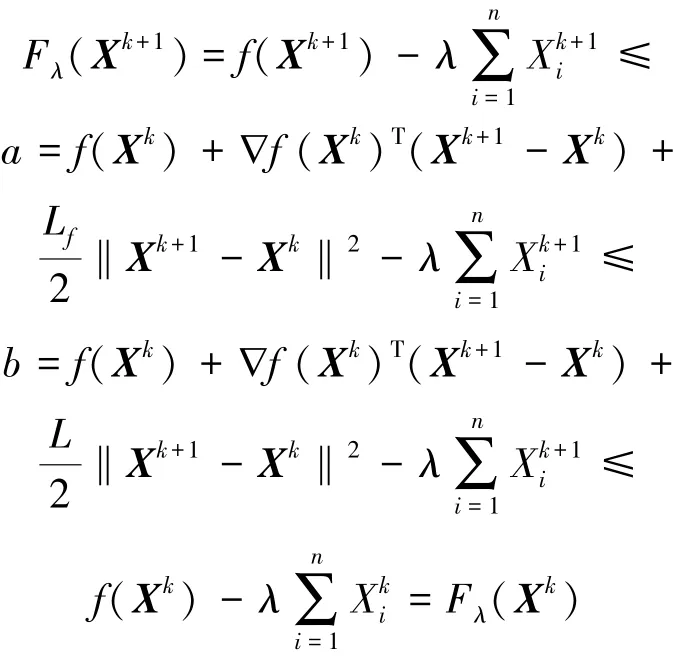
最后一个不等式成立是因为Xk+1是问题(7)的最优解。 进而有：

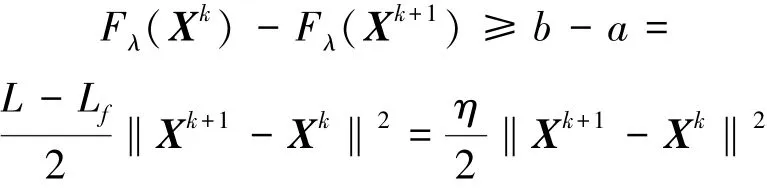
这说明序列{Fλ(Xk)} 是单调不增的。

因为f(X) 在[0, 1]n上有下界, 所以Fλ(X) 在[0, 1]n上也 有下 界。 结合 序 列{Fλ(Xk)} 的单调性可知, 序列{Fλ(Xk)} 是收敛的, 再根据上述最后一个不等式可得：

结合序列{Xk} 的有界性可得序列{Xk} 是收敛的。 证毕。

引理1假设是问题(6) 的一个最优解, {Xk} 是算法1 生成的序列, 若存在k ∈N 使得, 则有。

证 因为X*λ是问题(6) 的一个最优解, 所以对问题(6) 的任一可行解X 有：

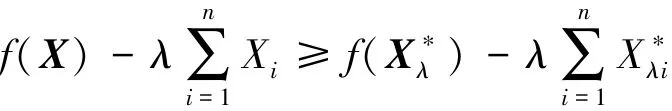
因为∇f(X) 是李普希茨连续的, 则有：

根据这两个不等式, 可得：

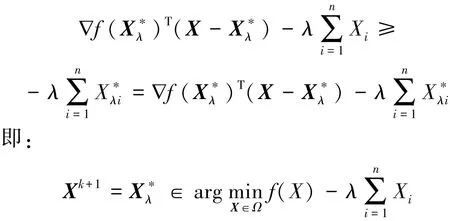
根据上式可知, 若存在k ∈N 使得Xk= X*λ, 则根据算法1 的第3 行有Xk+1= X*λ。 证毕。

定义1对给定的常数L ＞0, 向量X ∈Ω1称为问题(4) 的一个L- 稳定点, 如果：

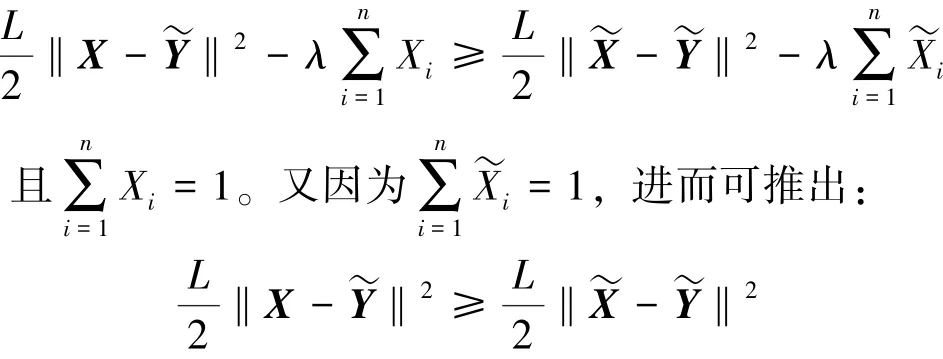
这说明X˜是问题(4) 的一个L- 稳定点。 证毕。

证 根据函数h(⋅) 的定义和投影函数∏[0,1](⋅) 的性质, 可知h 是一个分片线性单调不降的连续函数, 且{ - L(- ω)： ω ∈{0,1}, i ∈Bk, j ∈{1, 2, …, n0}} 是它的所有连接点。 因为：

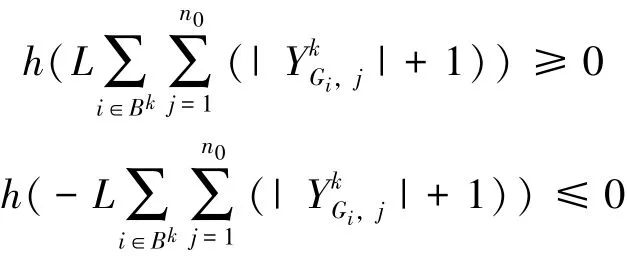
所以h 在R 中必有一个根λk。 将h 的所有连接点去重并假设去重后连接点的个数为l, 按升序排列, 得到{ci： i = 1, 2, …, l, c1＜c2＜… ＜cl}。 再用二分搜索找p ∈{1, 2, …, l - 1} 满足h(cp) ≤0 且h(cp+1) ≥0。 若h(cp) = 0 或h(cp+1)= 0, 找到λk。 若h(cp) ≠0 且h(cp+1) ≠0, 此时有h(cp) ＜0 ＜h(cp+1), 则由下式

找到λk。 证毕。

基于算法1 和定理4, 提出一种启发式算法求解问题(4), 用启发式算法来确定组指标集Bk和λk, 用算法1 来确定Xk+1。

算法2

输入： L(L ＞Lf), λ, X0；

输出： X*；

1： 初始化： k ←0；

2： 重复

3： Bk←最大的s 个H(YkGi) 的指标集中指标最小的一个；

4： λk←根据定理4 寻到的根；

5： Xk+1←Γλk(Xk)；

6： k ←k + 1；

7： 直到满足终止条件；

8： X*←Xk。

3 数值实验

算法2 中, 每一轮迭代都用固定的L, 这显然不是最优的方式。 若Lf设置得过大则步长过小, 需更多轮迭代。 然而, 要确定一个一般形式的函数的最小李普希茨常数Lf是困难的, 为此在算法2 的基础上, 结合了非单调线搜索算法来动态更新L 的值, 给出下面的非单调迭代组软阈值算法 (Nonmonotone Iterative Group Soft Thresholding,NIGST), 其中Sk= ∇f(Xk) - ∇f(Xk-1), ΔXk= Xk- Xk-1。

算法3X*←NIGST(L, λ, X0)

输入： Lmin, Lmax, L0, X0, ε ＞0, 最大迭代轮数；

输出： X*；

1： 初始化： k ←0, L0∈[Lmin, Lmax],L0＞Lf；

2： 重复

3： Bk←最大的s 个H(YkGi) 的指标集中指标最小的一个；

4： λk←根据定理4 寻到的根；

5： 重复

10： k ←k + 1；

11： 直到满足终止条件；

12： X*←Xk。

下文将算法3 用于模拟数据的组指数跟踪实验, 来展示算法3 的性能。 所有的实验都在一个带双Intel Xeon 处理器E5-2665, 16cores, 2.4GHz,32GB 的平台的软件Matlab R2017b 上执行。

组指数跟踪的目的是复现给定市场指数的表现和风险概况, 并构建一个组稀疏指数跟踪投资组合, 使得投资组合的表现尽可能接近市场指数的表现[2,4,7], 要解决的问题如下：

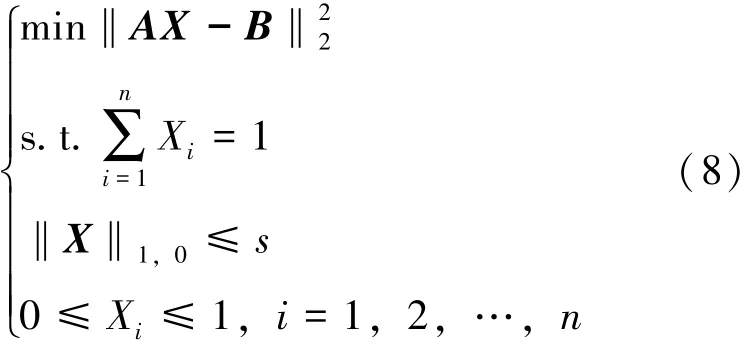
其中A∈Rm×n是收益矩阵, Aij是第j 个资产在第i个阶段的收益, B∈Rm是市场指数的收益向量,X∈Rn是想要找的比例向量, Xi表示第i 个资产占总投资额的比例。 X 满足至少N-s 组元素为零组。

算法3 的最大迭代轮数为5000。 关于非单调线搜索的参数, 设置M = 6, c = 10-6, γ = 2,Lmin= 10-8, Lmax= 108。

对所有实验的模拟数据, 分别记真实比例向量和恢复比例向量为X+和X*。 生成服从独立同分布的高斯矩阵A+∈Rm×n(m＜＜n) 和真实比例向量X+∈Rn, 其中X+的元素被分成N 组, 每组有n0个元素, 即n = Nn0。 随机选取N 组中的s组作为可能的非零组, 同时令其余N-s 组为零组。 在s 组可能非零的组中, 每个元素都服从均匀分布, 且对于X+, 这s 组所有元素的和为1。接着通过B = AX+来生成B。 实验参数( A 的行数,A 的列数,X+元素的组数,每组的元素个数,非零组占比最大值)用元组(m,n,N,n0,s)表示。

若无额外说明, 对于给定的参数组, 每个实验结果都是取100 次相同实验结果的平均值。 衡量实验结果质量的指标有3 个, 分别是相对误差‖X*-X+‖ /‖X+‖, 恢复的成功率和CPU 耗时。 一次成功恢复的定义为相对误差小于预设的ε, 这里设ε= 10-6。

下面通过1 组实验来展示算法3 的性能(见表1), 固定采样率m/ n 分别为1 / 4 和1 / 3, 测试算法3 在不同的规模和稀疏度下的性能。

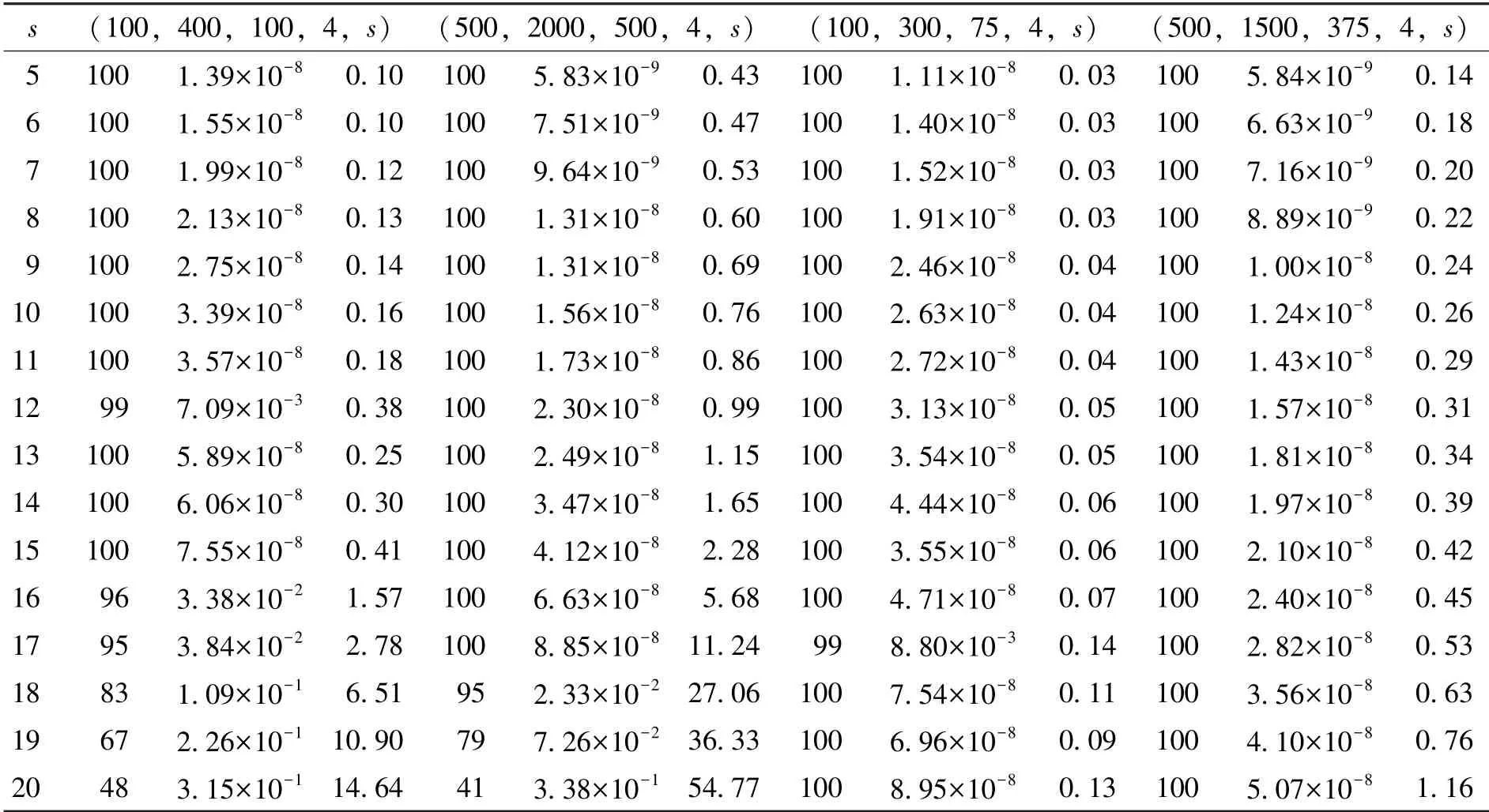
表1 不同采样率和规模下的成功率、 相对误差、 CPU 耗时

根据表1, 可以得出两个结论： 1) 规模更大的例子, 结果更加准确, 有更高的成功率； 2)采样率更高的例子, 成功率更高, 相对误差更小, 耗时更短。

4 结论

对带组基数约束的投资组合问题, 本文将其拉格朗日对偶问题的内部问题近似转化为可用迭代软阈值算法求解的形式, 证明了对于给定的拉格朗日乘子, 文中的算法1 在一定条件下收敛到原问题的一个L-稳定点。 为使得算法每轮的迭代点满足分量和为1 的约束, 在算法1 的基础上,结合一种寻找的启发式算法, 来满足根据定理1中的阈值算子求得的解分量和为1, 并提出启发式算法2。 在算法2 的基础上, 结合非单调线搜索算法, 得到算法3。 从模拟数值实验的结果观察到, 在采样率不低于1 / 4 且稀疏度不高于15%时, 算法3 实验结果的相对误差基本上能下降至10-8以下, CPU 耗时较短且算法结果稳定。