BP 神经网络预测复杂聚合物体系浊点数据

何素贞

( 莆田学院 机电工程学院， 福建 莆田 351100 )

0 引言

高分子聚合物是由键重复连接而成的高分子量化合物[1], 而聚合物分离膜是一种具有选择透过性质的膜, 利用该性质可实现物质的分离、提纯以及浓缩等。 目前, 聚合物分离膜的主要制作方法是采用浸没沉淀法[2], 该方法的制备前提是要选择合适的铸膜液； 为此, 很多学者对铸膜液的性质进行了研究。 研究表明, 三角相图可直观地表征铸膜液的热力学性质, 而三角相图的绘制需要准确获得体系在特定温度下的浊点线,因此获取体系的浊点数据成为绘制三角相图的关键之一[3]。 目前, 获取体系的浊点数据通常采用浊点滴定实验法和热力学计算法[4-5]。 但对于复杂的高浓度聚合物体系的热力学理论模型, 因其非线性约束十分复杂, 上述两种方法仍难以获得较为准确的浊点数据。 为此, 何雪忠等利用基于Levenberg-Marquardt (LM) 算法的BP 神经网络成功地预测了复杂聚合物体系的浊点数据[6-7], 但该算法模式识别处理较弱, 易产生过拟合。 基于此, 本文提出一种基于贝叶斯正则化(Bayesian regularization, BR) 算法[8]训练神经网络的方法来获得聚合物溶液体系的浊点数据,并通过模拟验证了该方法的有效性。

1 BP 神经网络与BR 算法

1.1 BP 神经网络

BP 神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络[9]。 BP 神经网络工作的主要流程： 1) 输入的信息数据通过映射得到一组输出数据, 然后将该输出数据与期望输出数据进行比较得出误差； 2) 利用误差对权重求偏导得出梯度, 然后再利用梯度不断调整网络权值和偏置, 直到误差达到最小或者达到最大迭代次数, 以使网络的最终输出与期望输出尽可能接近, 从而达到训练的目的。 图1 为多层神经网络结构及其训练流程图。 该神经网络由多层神经元组成, 第1 层是输入层, 中间层为隐含层, 最后1 层为输出层。

图1 BP 神经网络简要结构和流程图

令输入值为：

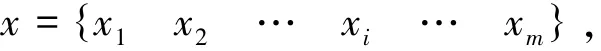
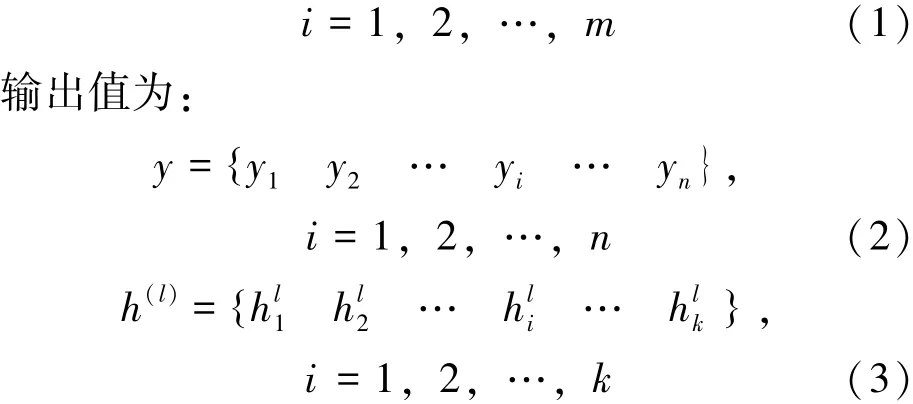
式(1) ～(3)中： m、 n 分别为输入层和输出层的节点数； k 为各隐含层神经元的个数； hli=f(netli), hli为第l 隐含层第i 个神经元的输出, f为神经元的激活函数,为第l 隐含层第i 个神经元的输入, Wlij为第l - 1隐含层第j 个神经元与第l 隐含层第i 个神经元之间的连接权重, bli为第l 隐含层第i 个神经元偏置。 因为BP 神经网络的误差函数的梯度值是由反向传播算法来计算的, 所以BP 神经网络会存在以下问题： 基于多层网络的梯度下降训练易使网络陷入误差曲面上的某个局部极小值； 当网络中隐藏节点过多时, 因空间维数过高易导致训练后期出现过拟合[10]。

1.2 BR 算法

因传统BP 神经网络在训练过程中会对训练样本中包含的抽样误差进行拟合, 这会使网络出现过拟合现象, 即在训练集上表现出误差较小,而在测试集上表现出误差较大。 BR 算法是一种基于贝叶斯框架选取正则化参数的算法, 它可以通过修正神经网络的误差函数来防止过拟合的出现[11]； 因此, 本文利用BR 算法来控制模型复杂度以及约束要优化的参数, 以此提高模型的泛化能力。

一般情况下, 神经网络的误差函数采用均方误差函数(Emse), 表示为

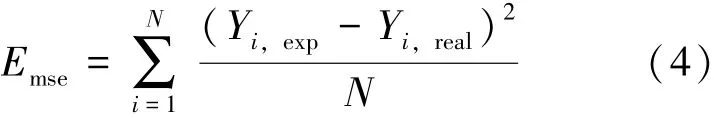
式(4)中： Yi,exp表示期望输出值, Yi,real表示实际的输出值, N 表示样本数。 在BR 算法中, 网络误差函数F 是在上述误差函数后加上权衰减项Ew, 即

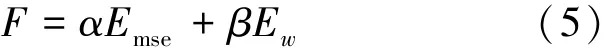
2 预测与分析

2.1 水-二甲基乙酰胺-聚砜成膜体系的BP 神经网络预测

根据水-二甲基乙酰胺-聚砜成膜体系的构成, 以体系的温度和聚砜的质量分数作为网络输入、 以体系中的水和二甲基乙酰胺的质量分数为网络输出构建BP 神经网络, 算法流程如图2 所示。 该神经网络隐含层有10 个神经元, 其传递函数为tansig()； 输出层有2 个神经元, 其传递函数为线性purelin ( )。 模型的训练函数采用trainbr(), 表明采用基于BR 算法的BP 神经网络。 神经网络预测前需要归一化数据, 以避免因输入输出数据数量级差别较大而造成网络预测误差较大, 训练终止误差≤10-5, 本文采用文[12]中的实验数据实现训练与预测, 其中55 组数据为训练样本, 剩下33 组数据为测试样本。

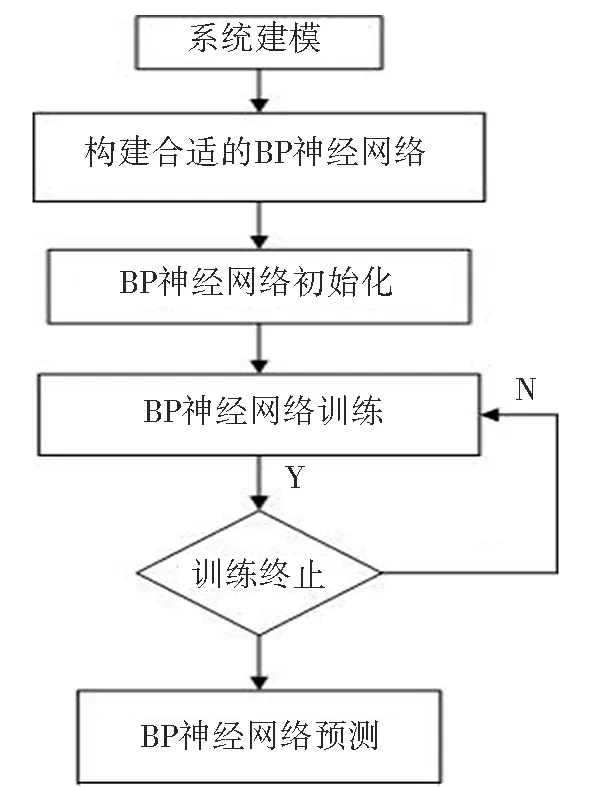
图2 算法流程图

2.2 结果分析

分别利用基于BR 算法和基于LM 算法的BP神经网络对水和二甲基乙酰胺的质量分数进行预测, 结果如图3～图6 所示。 由图3～图6 可直观地看出, 利用基于BR 算法的BP 神经网络对水和二甲基乙酰胺质量分数的预测数据更多地落在y=x 直线上, 这表明该算法预测的数据与真实的实验数据更为接近。

图3 基于BR 算法的BP 神经网络对水质量分数的预测结果

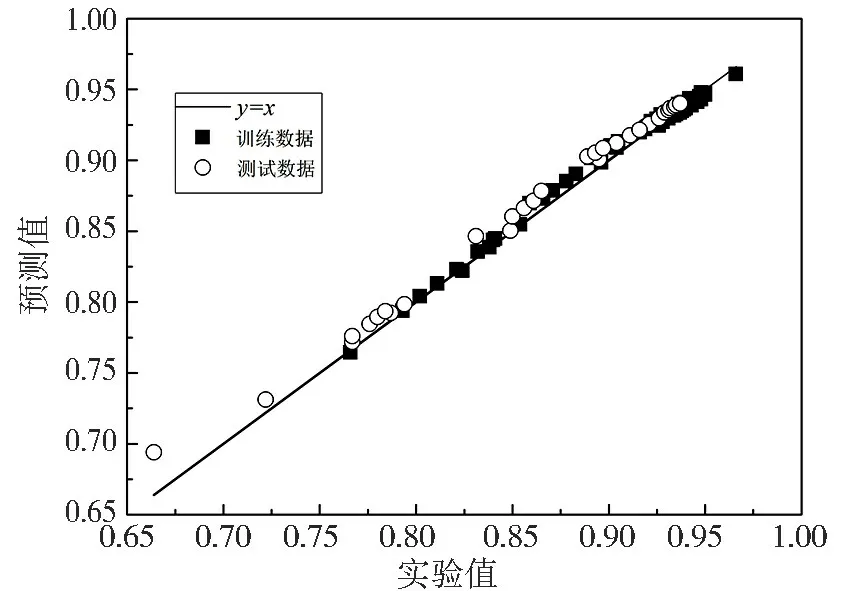
图4 基于BR 算法的BP 神经网络对二甲基乙酰胺质量分数的预测结果

为了定量比较基于这两种算法的预测性能,本文采用平均相对误差( MRE) 来衡量这两种算法。 误差的计算公式为

表1 为利用式(6) 计算所得的基于LM 算法和基于BR 算法的BP 神经网络预测相对误差。 从表1 可以看出, BR 算法在对水和二甲基乙酰胺质量分数的预测上明显优于LM 算法。 表2 为LM算法和BR 算法的收敛速度。 由表2 可以看出,BR 算法的收敛速度明显快于LM 算法。

图5 基于LM 算法的BP 神经网络对水质量分数的预测结果

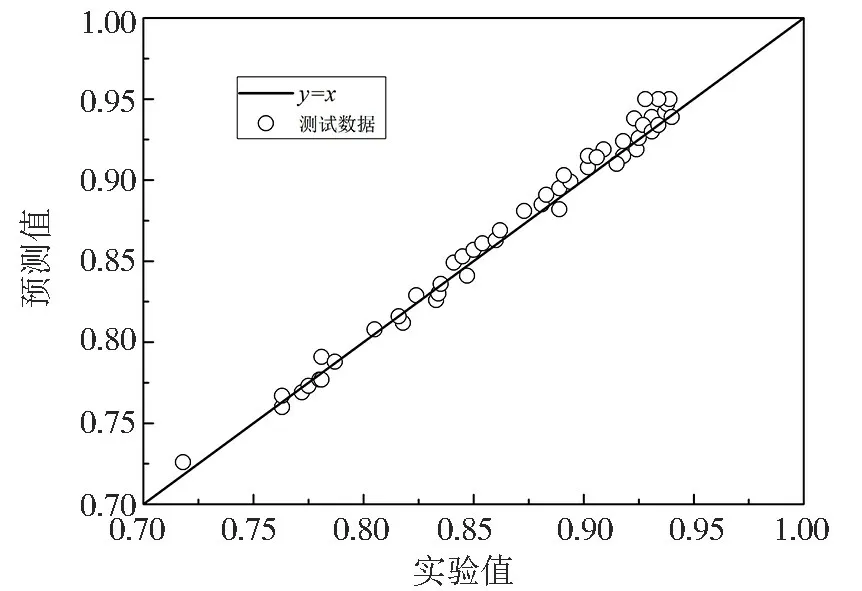
图6 基于LM 算法的BP 神经网络对二甲基乙酰胺质量分数的预测结果

表1 基于LM 算法和BR 算法的BP 神经网络预测的相对误差

表2 LM 算法和BR 算法预测不同物质的收敛速度(迭代次数)

3 结论

本文利用基于BR 算法的BP 神经网络对水和二甲基乙酰胺的质量分数进行预测, 结果表明该方法在准确度和速度方面明显优于基于LM 算法的BP 神经网络, 因此该方法可以为成膜体系的相平衡研究以及膜制备提供更为准确的数值依据。