挖掘教材价值 培育数学思维之花
——小学数学教学中学生数学思维能力培养的策略
江苏省盐城市第一小学教育集团聚亨路校区 刘海萍
教材呈现的是静态的基本素材、基本内容和基本方法,教师在教学时应充分挖掘学生身边的暗含着某种数学现象或数学规律的数学问题,关注学生的障碍点和发展点,引导学生用数学方法描述变量之间的数量关系。苏教版《义务教育教科书·数学》六年级上册第42 页思考题,主要是让学生在探索和应用计算规律的过程中,体会分数乘法中存在的一些有趣现象,发展学生的数学思维能力,感受数学的结构美,激发学生学习数学的兴趣。我在教学时既基于教材又高于教材,使静态的文本材料演示成动态的教学过程,真正体现为学习而教,为生长而教。结合这道“思考题”,我做了精心的设计,开发成一节有梯度的思考题专题课。教学设计环环相扣,层层递进,引导学生深度学习,培养学生深度思维,体现了探索精神,真正促使学生形成数学素养。
一、基于经验,让学生的思维有根
杜威指出:“一盎司的经验胜于一吨的理论,只是因为在经验中,任何理论才具有充满活力和可以证实的意义。”数学的学习要基于学生已有的知识经验和认知水平,基于学生已经具备的基础知识、基本技能。规律的探究要以经验为根系、以旧知为土壤,让经验之根更深。
片段一:唤醒经验,导入新课
出示四道计算题。
请学生口答每道题的结果。追问:运用什么方法可以使计算简便?
小结:整数的运算律和一些性质对于分数同样适用,巧用运算律和性质可以使计算更加简便。其实,分数运算中的技巧还有很多,今天这节课我们就来研究分数运算中的巧算。
【思考】通过口答四道简便计算题,我让学生再一次感受整数中的运算律和一些性质在分数计算中可以使计算简便,引出分数运算中的巧算,唤醒学生已有的经验,引发学生对分数运算中的技巧的探究兴趣,揭示本节课的研究课题。
二、基于方法,让学生的思维有干
小学生学习数学是一个思考的过程,思考是学生学习数学认知过程的本质特点,是数学的本质特征。可以说,没有思考就没有真正的数学学习。在平时的教学中,我发现:学生能够发现看似简单的算式背后隐藏的规律,但是却不能利用规律解决复杂的分数运算,究其原因,是因为解决这类问题时只注重了“巧”的教学,而忽略了“理”的教学。在课堂教学中,我试图在学生的学和思上做文章,在课堂中引发学生思考,让学生自主探究,把学生的思维引向深处。学生理解了规律形成的原因,发展学生的符号意识,体会分数运算中存在的一些有趣的现象和数学规律的探究方法,积累了探索经验,学生的思维顺着枝干发展,生长出了崭新的枝叶。
片段二:探究规律,解决问题
(一)探究规律
出示思考题。学生口算,提问:仔细观察,你有什么发现?同桌互相说一说。
思考:是不是所有的分数都有这样的规律呢?为什么分子是1,分母是相邻自然数的两个分数会有这样的计算规律呢?
学生结合算式解释规律形成的原因,再举例。
明确:因为这两个分数的分母是相邻的两个自然数,所以在求差时,它们的公分母就是这两个数的乘积,即求差的分母和求乘积的分母相等;再观察它们的分子,由于分子是1,所以两个分数的分子就是相邻两个自然数的差(也就是1),与积的分子相等。
引导学生用简洁的方式表示发现的规律,并利用发现的规律说出一组得数相等的式子。
(二)应用规律
出示:
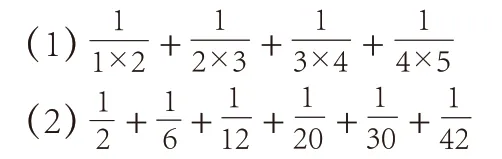
提问:仔细观察这两道题,有什么特点?利用通分的方法能解决吗?
小组讨论:有什么好的办法?能否利用我们发现的规律来解决?
揭示:像这样,把一个分数拆成两个分数相减的形式,然后再进行计算的形式,叫作拆分法。
变式练习:
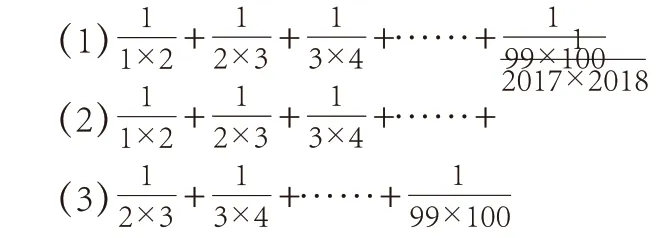
(三)回顾反思
提问:回顾我们刚才的学习过程,是怎么研究的?
小结:从简单的算式入手,观察算式的特点,发现隐藏的规律,并应用规律解决问题。
【思考】通过一组有价值的口算,产生研究需求和研究素材。引导学生通过计算、观察、比较,发现算式背后所隐藏的规律。引发思考:为什么分子是1,分母是相邻自然数的两个分数会有这样的计算规律,理解了规律形成的原因。并适时引导学生用数学符号语言来表示规律,发展学生的符号意识。接着,利用规律说出一道得数相等的式子,加深学生对数学算式中的规律的理解,体会分数运算中存在的一些有趣的现象,这是对规律认识和理解的拓展,对学生思维的要求更进一步。再通过讨论交流,自主尝试,并汇报交流,揭示复杂的分数运算可以运用规律利用拆分的办法转化成简单的运算。加数由少变多,由完全直观到部分直观,对学生想象能力、分析能力提出了较高的要求。我最后组织学生进行了有效的回顾与反思,使学生对数学规律的探究方法有了清晰的认识,也为接下来的探究提供了方法,积累了经验。
三、基于数学思想,让学生的思维开花
数学思维的训练要有机渗透数学思想方法。怎样才能既在数学教学中渗透数学基本思想,又能注意在数学思想的渗透时做到自然贴切、不露痕迹?在教学设计中,教师要恰当把握数学思想的渗透,提升学生的数学素养,让学生的思维“开放出娇艳的花朵”。
片段三:回顾反思,深化理解
出示:
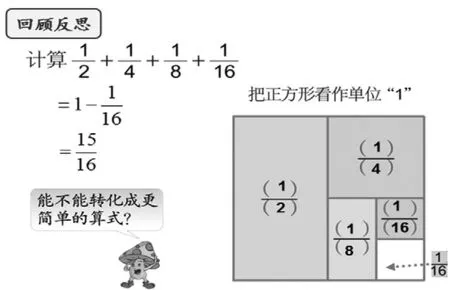
回顾:这是我们五年级的时候做过的一道题,我们原来是怎么解决的?
小结:把算式和图形联系起来,也就是数形结合思想的运用。
引发思考:这道分数计算的算式有什么特点?利用拆分的办法如何解决?
【思考】通过回顾五年级解决过的数学计算题,揭示无论是用拆分的方法还是数形结合的方法,都可以把复杂的算式转化成简单的算式来解决,学了新方法,不忘老方法。我在带领学生探索规律并运用规律解决问题的过程中,有机渗透了等值转化、数形结合等数学思想。
四、基于数学文化,让思维之花更艳
兴趣是学习的前提,是思维的动力。数学文化的渗透,可以激发学生学习数学的兴趣。通过介绍“埃及分数”,渗透数学文化,让学生了解“埃及分数”与所学知识的关系,并进一步拓展延伸,鼓励学生课后进一步研究有关“埃及分数”中所隐藏的知识和规律,学生的思维之花更加艳丽。
片段四:总结全课,文化渗透
交流:通过今天的学习,你有哪些收获?
引出“埃及分数”,埃及同中国一样,也是世界上著名的文明古国。人们在考察古埃及历史时注意到像阿基米德这样的数学巨匠,居然也研究过“埃及分数”。原来古代埃及人没有几分之几的概念,在他们的心目中,当东西分不出整数个时,就先分出几分之一,再分出几分之一,古埃及人很早使用的分数都是分子是“1”的分数,所以分子是“1”的分数称为“埃及分数”。
【思考】计算教学,以知启智。数学教学的核心目标是培养学生的思维能力,通过计算发展学生的创新思维,这既是计算教学的重要目标,也是数学教育的永恒追求。我试图通过思考题的教学研究,彰显思考题的教学价值,让学生在有梯度的引导下,经历思考的过程,将学生的思维引向深处,使学生的数学思维在课堂中生长。借助这个载体让学生感悟、掌握其中的思考元素,从而获得更有意义的思维发展,这样的课堂才会展现出数学教学最本真的价值。

