基于蚁群算法的起重机变幅控制系统动态特性研究*

张 锦，唐友亮

(宿迁学院,江苏 宿迁 223800)

0 引 言

汽车起重机作为工程机械重要组成部分之一，被广泛应用于路面、桥梁等各种大型工程中，为适应各种复杂施工工况，汽车起重机朝着智能化方向发展[1]。汽车起重机变幅液压缸位置控制性能是实现汽车起重机智能控制的重要方面。

魏乐[2]对50 t汽车起重机的变幅系统进行了分析，基于AMESim软件对其进行建模仿真，对不同工况下的仿真结果进行了分析，重点对影响变幅性能的主要元件—平衡阀的相关物理量进行了分析研究，论证了其在变幅系统中的重要作用；张平格等[3]以50 t汽车起重机变幅液压系统为研究对象,基于AMESim软件建立变幅液压系统仿真模型，以平衡阀中液控口阻尼孔和控制弹簧腔阻尼孔的动态平衡为切入点，进行了仿真分析与研究，为液压起重机的优化设计提供了参考；姚泽光等[4]以QY8A汽车起重机的变幅机构为研究对象，利用AMESim建立了其液压系统模型，通过设置主要参数，实现了液压系统的仿真；仿真结果直观地反映了起重机变幅起升过程中系统的动态特性,以便对其进行优化设计；张振伟等[5]通过AMESim软件进行了仿真分析，分析了平衡阀控制特性，以及控制腔压力阶跃上升、下降响应和抑制负载波动响应，并进行了平衡阀台架试验，试验数据与仿真数据的数值误差较小，平衡阀开闭特性、过补偿能力和微动特性较好，但平衡阀抗干扰能力、对负载波动抑制能力还有待进一步改善。

对汽车起重机变幅系统的研究可知，目前关于汽车起重机变幅系统的研究较多，但主要集中于系统中平衡阀的研究，针对提高变幅液压缸位置控制精度的研究较少。

因此，笔者设计汽车起重机变幅液压缸位置控制系统，在建立控制系统数学模型基础上，分别采用Ziegler-Nichols算法、蚁群算法和果蝇算法对PID参数进行优化，并对加入不同算法优化的PID参数的系统控制性能进行仿真分析。

1 变幅液压缸位置控制系统

汽车起重机变幅系统主要由起重臂和变幅液压缸组成，如图1所示。

图1 汽车起重机起重机构组成

变幅液压缸活塞杆伸出，起重臂仰起，幅度减小；变幅液压缸活塞杆缩回，起重臂下降，幅度增大。

笔者设计的控制变幅液压缸活塞位移的电液控制系统，如图2所示。

图2 控制变幅液压缸运动的电液控制系统

笔者将汽车起重机常采用的电磁换向阀换成控制精度更高的比例换向阀，变幅液压缸的运动由比例换向阀阀芯运动进行控制，从而实现对起重臂仰起幅度和下降幅度的精确控制。

2 位置控制系统数学模型

液压缸活塞与汽车起重机起重臂一端连接，活塞带动起重臂运动，实现起重臂幅度的调整。该系统为典型的液压缸位置控制系统，其数学模型建立方法比较完善，本文列举系统关键环节数学模型[6]。

比例放大器数学模型为：

I=K1Δu

(1)

式中：Δu—输入电压；I—输出电流；K1—放大系数。

比例换向阀数学模型为：

(2)

式中：xv—阀芯位移；Kb—阀芯位移与电流增益系数；wm—比例阀固有频率；ξm—为比例阀阻尼比。

位移传感器数学模型为：

Uf=Kfxp

(3)

式中：Kf—位置反馈增益；Uf—反馈电压；xp—活塞输出位移。

活塞杆伸出时活塞杆位移xp对阀芯位移xv的传递函数为[7]：

(4)

活塞位移Xp对负载干扰FL的传递函数为：

(5)

3 位置控制系统控制器设计

液压缸位置控制常采用PID控制器，因此本文采用适应于计算机控制的增量式PID控制器[8]，该控制器表达式如下：

PID控制器中，最重要的是对比例、积分和微分3个参数的优化[9]。PID参数优化方法很多，本文分别采用Ziegler-Nichols算法、蚁群算法和果蝇算法，对PID控制器的3个参数进行优化。

笔者首先采用Ziegler-Nichols算法[10]。具体过程为：把积分系数和微分系数置零，逐渐增大比例系数，当系统产生振荡时，此时Kp就等于Kmax，系统振荡周期为Tc；其次，将比例系数缩小一个设定量，再按振荡周期Tc设置积分系数和微分系数。

经Ziegler-Nichols算法优化后得到的PID参数结果，如表1所示。

表1 Ziegler-Nichols算法优化PID参数结果

其次笔者采用果蝇算法优化PID参数[11]，其结构框图和流程图如图3所示。

其具体过程如下：设置果蝇初始种群大小为30，迭代次数200；滚筒位置调节器3个参数Kp、Ti和Td的初始取值为20、0.5和0.05，搜索范围设置为(0，100)；并采用ITAE作为指标函数，即：

(7)

经过200代迭代，果蝇适应度提高，可获得果蝇算法优化后的PID参数，如表2所示。

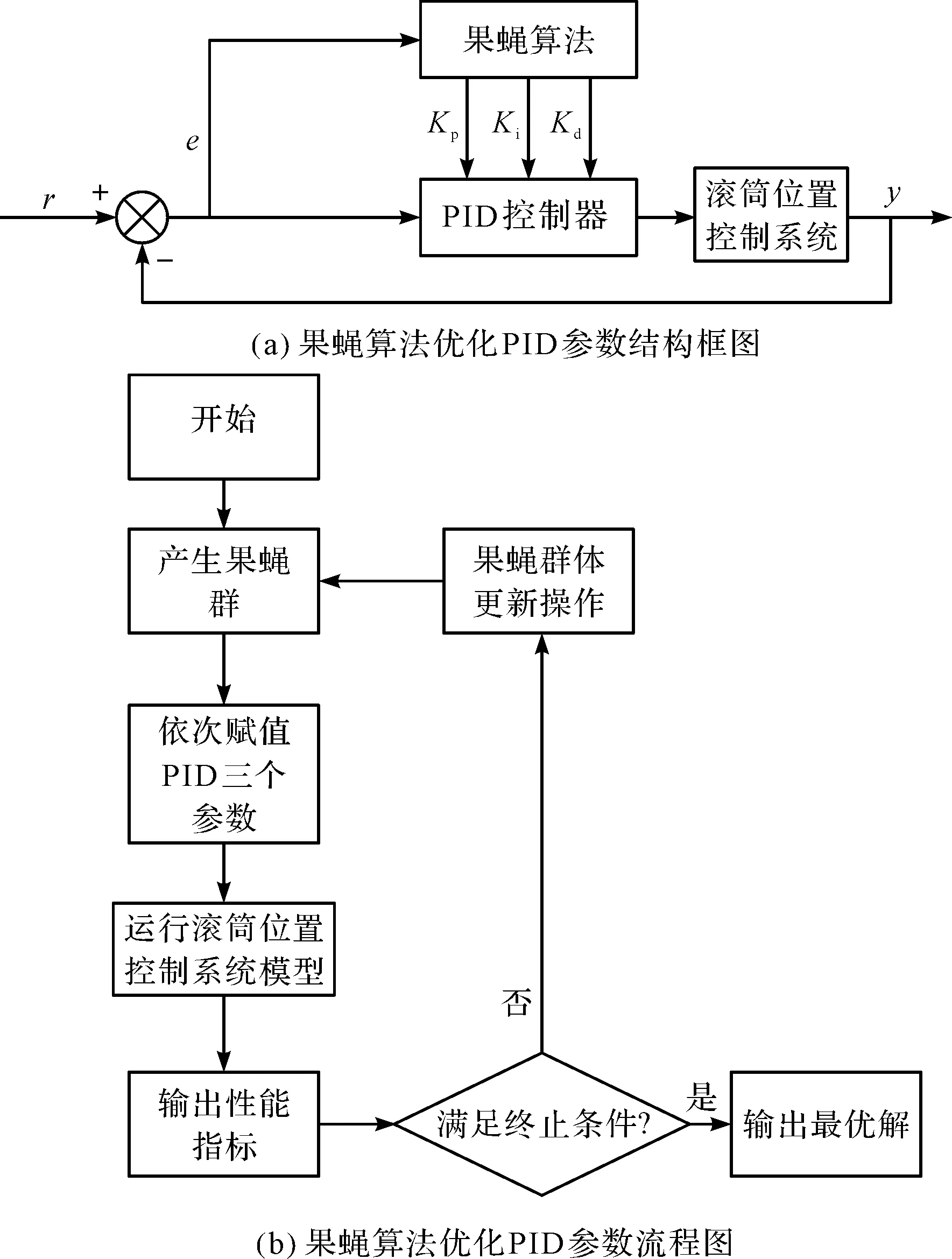
图3 果蝇算法优化PID参数结构框图及流程图

表2 果蝇算法优化PID参数结果

最后，笔者采用蚁群算法优化PID参数[12]，其结构框图和流程图如图4所示。

图4 蚁群算法优化PID参数结构框图

其具体优化过程为：设置蚂蚁数量为30，挥发系数ρ取0.8，信息启发因子α取0.3，最大迭代次数NC取200；限定起重臂幅度调节器3个参数Kp、Ti和Td范围设置为(0，20)；同样，采用ITAE作为目标函数。

经过200代迭代，可获得蚁群算法优化后的PID参数，如表3所示。

表3 蚁群算法优化PID参数结果

4 位置控制性能仿真分析

本文基于MATLAB/Simulink建立变幅液压缸位置控制系统仿真模型。为了对比仿真结果，在仿真模型中加入了基于果蝇算法、蚁群算法和Ziegler-Nichols算法优化的PID参数。

变幅液压缸位置控制系统仿真参数如表4所示。

首先对系统施加阶跃信号，经仿真得到系统阶跃响应曲线，如图5所示。

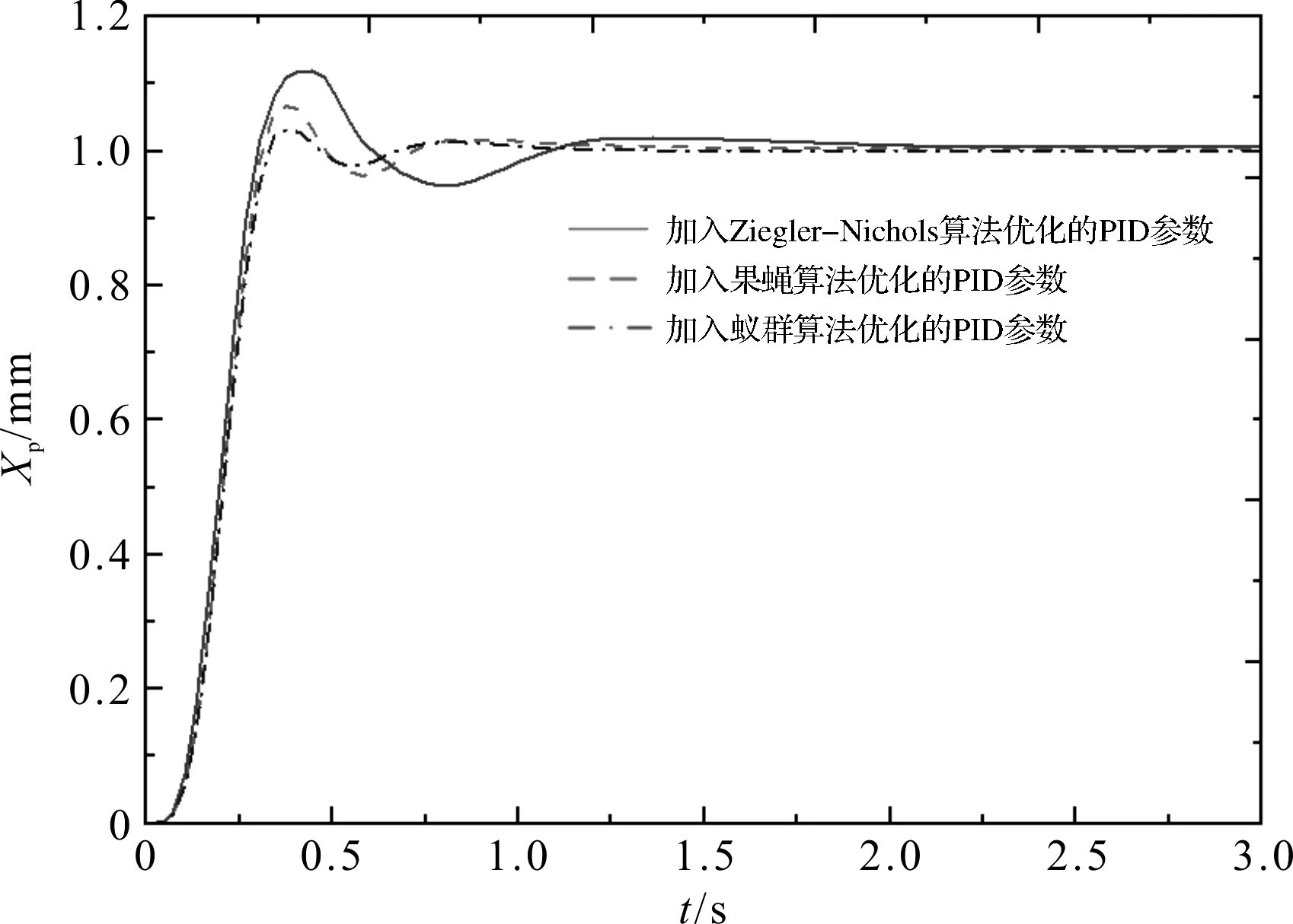
图5 阶跃相应曲线

加入3种算法优化PID参数后，系统阶跃响应曲线的超调量、调整时间和稳态误差对比情况，如表5所示。

表5 阶跃响应仿真结果

由表5可知：加入蚁群算法优化的PID参数的系统相比加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统，响应曲线超调量缩小了43.75%和20.59%，调整时间下降了49.82%和25.32%，稳态误差降低了53.57%和23.53%。

可见，加入蚁群算法优化的PID参数的系统阶跃响应性能，强于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统性能。

其次，对系统施加阶跃信号的同时，对系统施加随机干扰力信号，采用Simulink中的Uniform Random Number模块对系统施加0.01 kN～0.03 kN之间的随机干扰力，然后比较加入3种算法优化的PID参数的系统抗干扰性能。

仿真得到在随机干扰力作用下的系统阶跃响应曲线，如图6所示。

图6 加入随机干扰力的阶跃相应曲线

同样，采用超调量、调整时间和稳态误差3个指标，对加入随机干扰力信号的阶跃响应曲线进行评价，如表6所示。

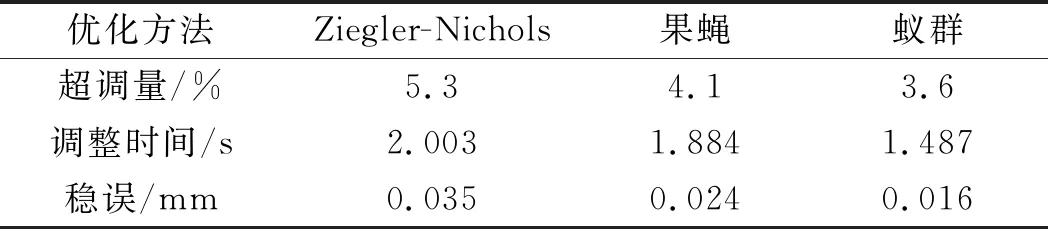
表6 加入随机干扰力的阶跃响应仿真结果

由表6可知：加入干扰力信号的变幅液压缸位置控制系统，加入蚁群算法优化的PID控制参数的系统相比加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统，响应曲线超调量缩小了32.08%和12.20%，调整时间下降了34.70%和26.67%，稳态误差降低了54.29%和33.33%。

可见，对比加入干扰力信号的变幅液压缸位置控制系统，加入蚁群算法优化的PID参数的系统抗干扰能力强于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统。

取液压弹簧刚度最小时的液压缸活塞杆位置作为初始位置，并对系统施加0.25 Hz正弦信号。

仿真得到加入不同PID参数的系统正弦响应曲线，如图7所示。

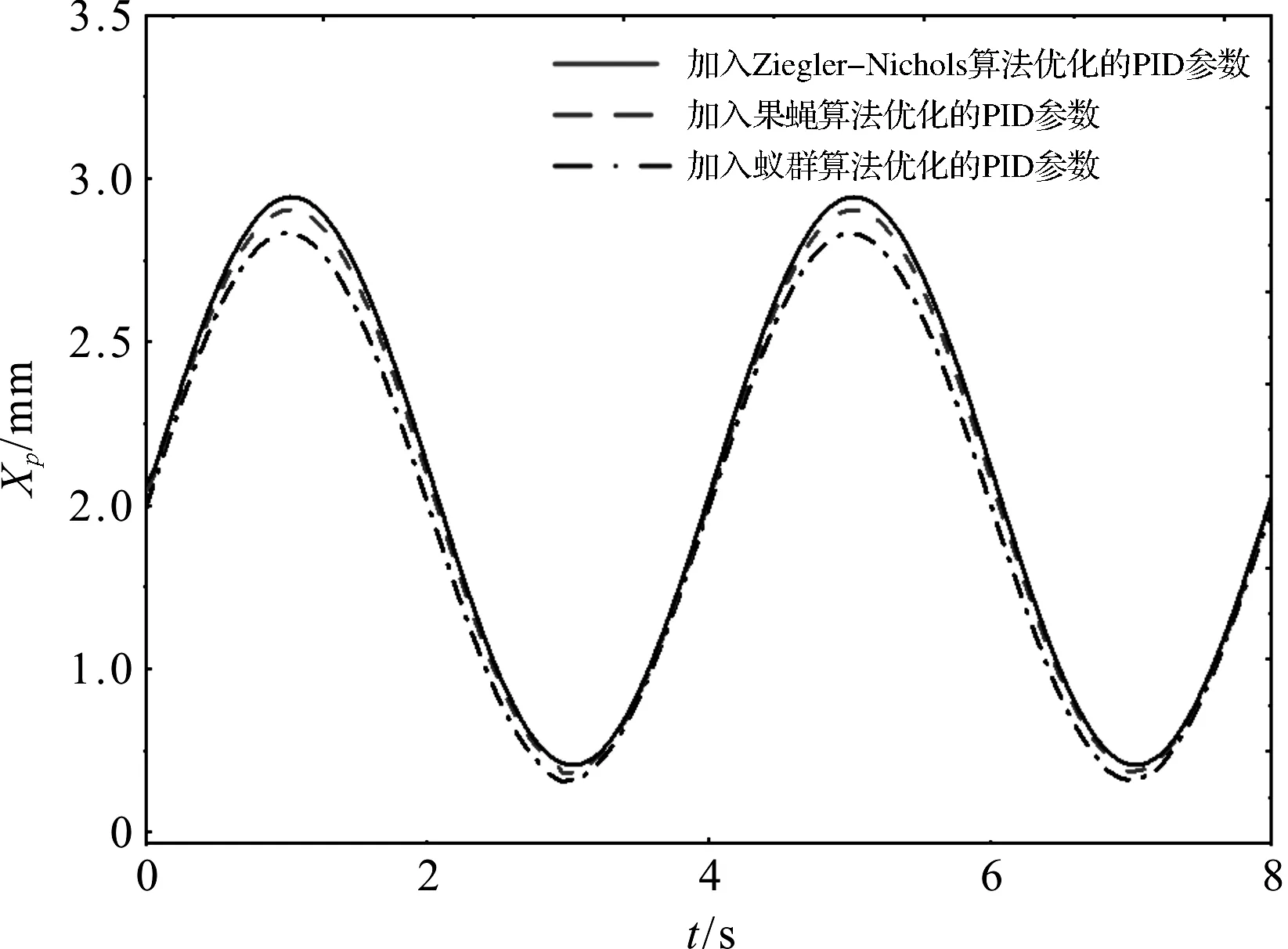
图7 正弦响应曲线

在0.25 Hz正弦信号下，加入不同PID参数的系统响应性能对比结果，如表7所示。

表7 正弦响应仿真结果

从表7可得：在0.25 Hz正弦信号下，加入蚁群算法优化的PID参数的系统相比于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统，最大跟踪误差缩小了44.737%和27.586%，平均跟踪误差缩小了47.059%和28.000%。

可见，对于0.25 Hz正弦信号后，加入蚁群算法优化的PID参数的系统响应性能优于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统。

其次，笔者在对系统施加正弦信号的同时，对系统施加随机干扰力信号(与阶跃信号所加随机干扰力信号相同)，并比较加入不同算法优化的PID参数的的系统抗干扰性能。

仿真得到在随机干扰力作用下的系统正弦响应曲线，如图8所示。

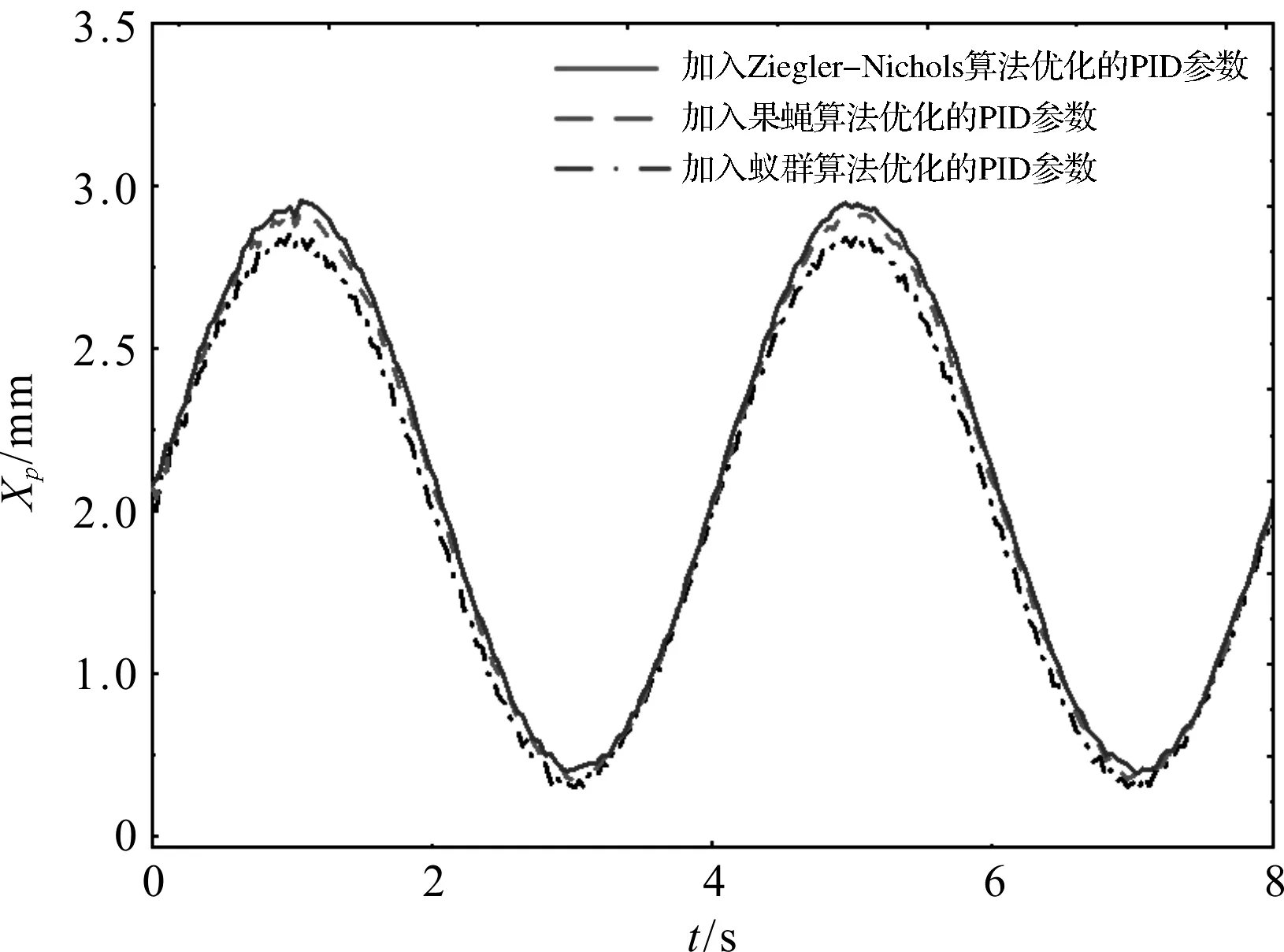
图8 加入随机干扰力的正弦响应曲线

在随机干扰力作用下，加入不同PID参数后的系统响应性能对比结果，如表8所示。

表8 随机干扰力作用下正弦响应仿真结果

从表8可得，在随机干扰力作用下，加入蚁群算法优化的PID参数的系统相比于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统，最大跟踪误差缩小了34.884%和22.222%，平均跟踪误差缩小了43.590%和29.032%。

可见，加入蚁群算法优化的PID参数的的系统抗干扰性能优于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统。

5 位置控制系统试验

为了验证加入蚁群算法优化的PID参数的系统实际控制性能，本文在XCT8L4_1型徐工汽车起重机试验台上进行试验，如图9所示。

图9 起重机变幅控制系统试验台

首先，进行阶跃信号响应试验，对系统输入幅值为1 mm的阶跃信号，进行起重机变幅控制系统响应特性测试和数据采集，得到系统阶跃响应性能实验曲线，如图10所示。

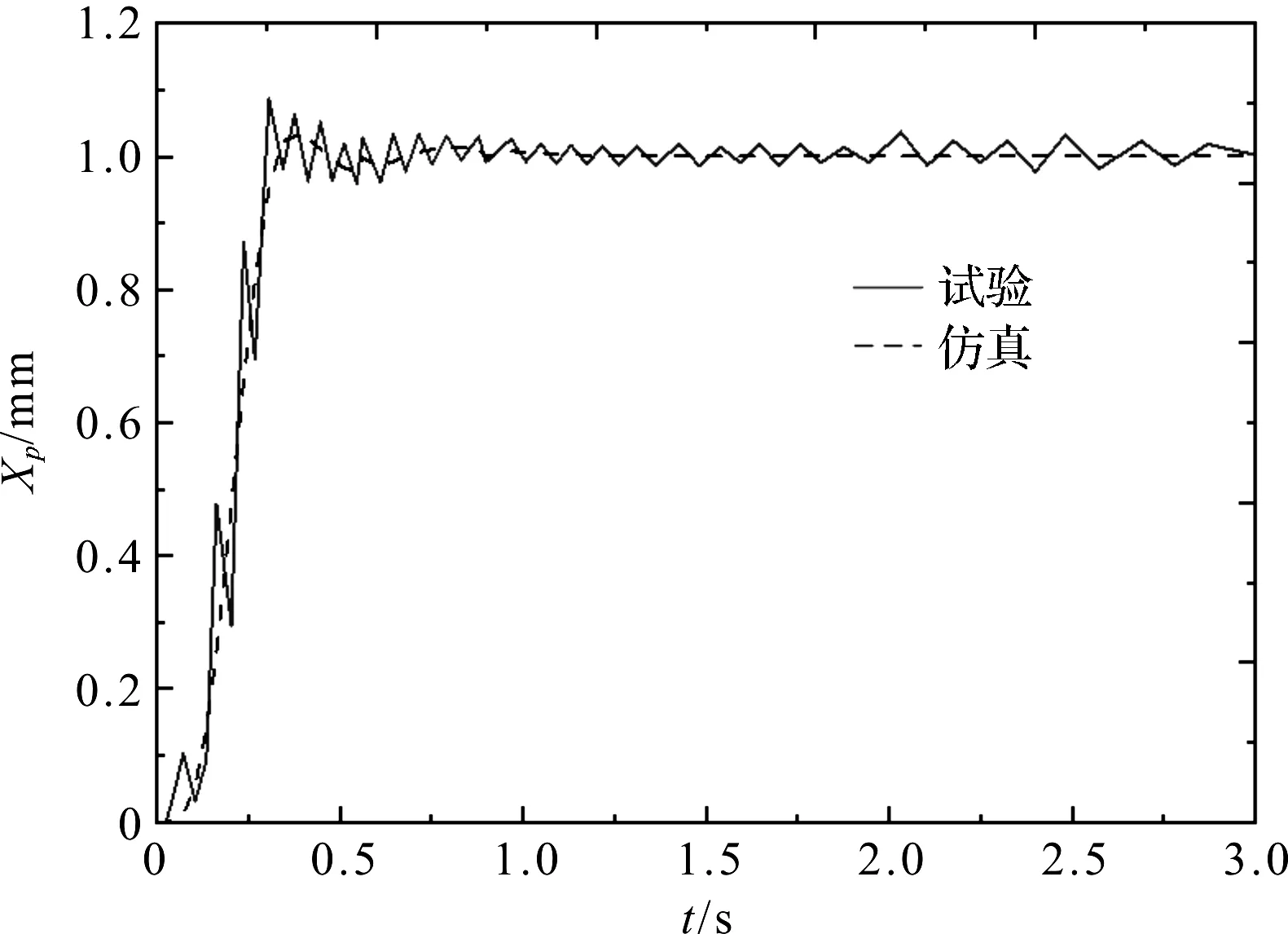
图10 系统阶跃响应性能实验曲线与仿真曲线

其次，对系统施加0.25 Hz正弦信号，得到系统正弦响应性能实验曲线，如图11所示。

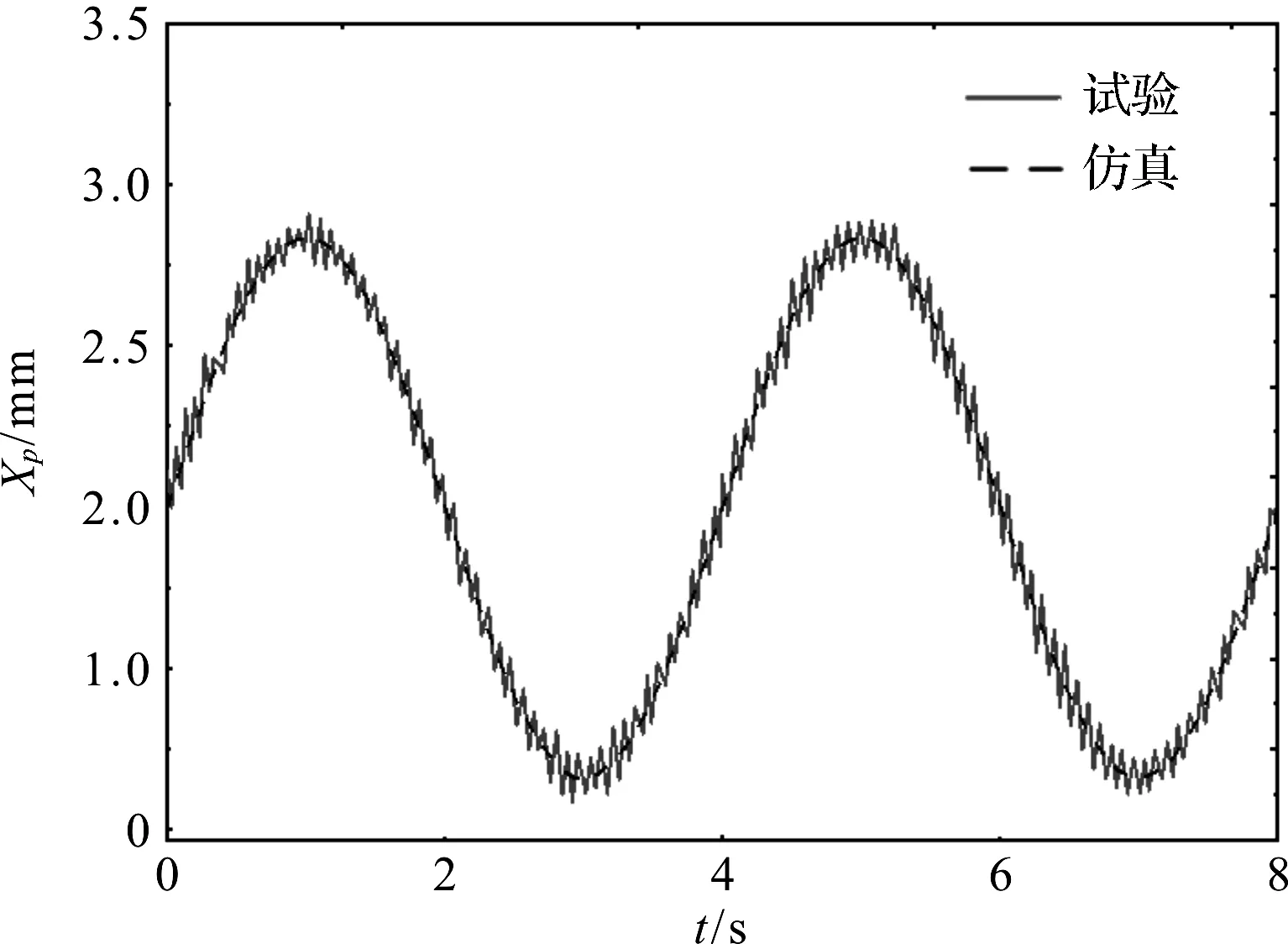
图11 系统正弦响应性能实验曲线与仿真曲线

本文使用相对误差e(i)，来评价经蚁群算法优化的系统阶跃响应性能和正弦响应性能。

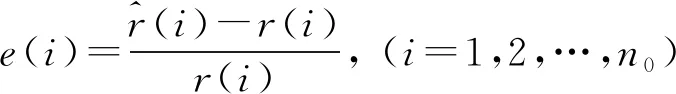
(8)

经数据整理后，可得到系统响应性能参数误差，如表9所示。

表9 系统响应性能参数误差

表9中，各误差为仿真与实验得到的系统性能参数误差。由表9可得：仿真得到的系统性能参数与实验得到的系统性能参数的误差不超过7%。

可见，加入蚁群算法优化的PID参数的的系统仿真结果和实验结果吻合度较高，很好地验证了仿真结论的正确性。

6 结束语

为提高汽车起重机变幅液压缸位置控制精度，笔者设计了汽车起重机变幅液压缸位置控制系统，在建立变幅液压缸位置控制系统数学模型基础上，分别采用Ziegler-Nichols算法、蚁群算法和果蝇算法对PID参数进行了优化，并对加入不同PID参数的系统控制性能进行了仿真分析，并通过试验台对系统实际控制性能进行了试验。

研究主要得到以下结论：

(1)从仿真结果看：加入蚁群算法优化的PID参数的的系统对阶跃信号和正弦信号的响应性能以及对随机干扰力的抗干扰性能均优于加入Ziegler-Nichols算法、果蝇算法优化的PID参数的系统；蚁群算法优化的PID参数相比Ziegler-Nichols算法、果蝇算法优化的PID参数，在加随机干扰力和不加随机干扰力两种情况下，系统阶跃响应超调量分别缩小了32%以上和12%以上，调整时间分别下降了34%以上和25%以上，稳态误差分别降低了53%以上和23%以上；对于正弦信号的最大跟踪误差分别缩小了34%以上和22%以上，平均跟踪误差分别缩小了43%以上和28%以上；

(2)从试验结果看：仿真得到的系统性能参数与实验得到的系统性能参数的误差不超过7%，加入蚁群算法优化的PID参数的系统仿真结果和实验结果吻合度较高，验证了仿真结论的正确性，说明加入蚁群算法优化的PID参数的系统更能满足汽车起重机对于变幅液压缸控制精度的要求。