关于泰勒公式的应用探究

周敬人

（湛江开放大学，广东 湛江 524000）

1. 泰勒公式[1]

2. 泰勒公式的应用

2.1 泰勒公式在计算函数极限中的应用

2.2 泰勒公式在近似计算中的应用

在高等数学学习中，利用带有拉格朗日余项的泰勒展开式作近似计算时，为定数，则其余项不会超过，从而可近似计算出某些数值，且估计出误差。

例3 计算 的值, 使误差不超过0.00001。

2.3 泰勒公式在正项级数敛散性判定中的应用

级数的通项公式可由不同类型的函数表达式所构成，而函数的表达式又非常复杂与繁琐，这时，可利用泰勒公式来简化级数，让运算过程更加简便。例5 讨论级数的敛散性解 利用泰勒公式展开，有

2.4 泰勒公式在广义积分的敛散性中的应用

在判断广义积分的敛散性时也可以利用泰勒公式进行判断，达到简化运算过程的效果。

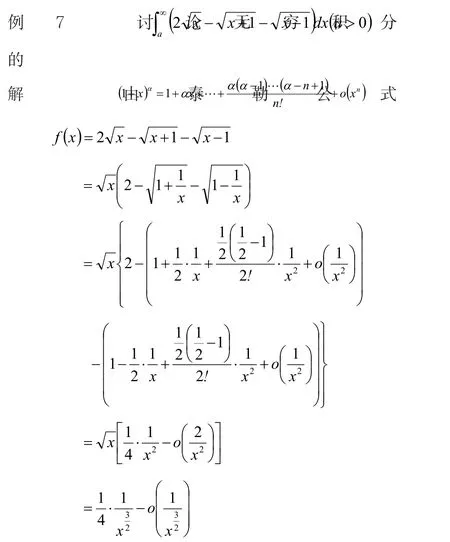
2.5 泰勒公式在求高阶导数及含有高阶导数的有关证明中的应用

2.5.1 泰勒公式求高阶导数

由于函数在某一点的带有佩亚诺型余项的泰勒公式是唯一的，因此，可利用这一性质求得函数在某一点的高阶导数。

2.5.2 证明与高阶导数有关的命题

当问题涉及函数的二阶或二阶以上导数的证明时,可根据题意对函数进行泰勒展开, 从而达到解决问题的目的。

3. 结论

文章对函数极限计算、误差的估计、级数与广义积分敛散性的判断、求高阶导数及含有高阶导数的有关证明等五个方面进行论述,探讨了泰勒公式的相关应用。