基于群体智慧的排序任务多聚合方法比较研究

杨 雷, 蔡依陶

(华南理工大学 工商管理学院, 广州 510640)

0 引 言

早在1906年, 伽尔顿把英国观众对一头牛的估计质量数值进行平均, 发现平均值非常接近于这头牛的真实质量。后来许多学者的研究表明, 汇总一群人的判断能产生一个比大多数个人更接近真实答案的估计, 这种现象被称为群体智慧[1]。群体智慧效应在单一数值估计的问题中(例如猜测玻璃瓶中红豆的数量)和多项选择问题中(例如在几个选项中选择某个国家的首都)得到了大量应用, 并取得不错的成果。群体智慧理论逐渐被运用于社会管理、 环境治理、 远程教育、 政治和经济预测以及电子商务等多方面领域。

然而许多现实实践形式的问题不能用一个连续的或离散的答案表示, 比如涉及多个元素排名的顺序问题, 笔者把群体智慧现象扩展到这种更复杂的排序任务问题中。排序问题起源于古时的政治投票体系, 早期的民主政体使用标准的简单多数投票方法, 每位投票人只能对偏爱的候选人投出一票, 得到票数最多的候选人获胜。简单多数投票方法存在很大的争议, 学者提出偏好排序投票取代前者。在偏好排序投票中, 投票者把候选人按照个人偏好列出顺序, 将所有投票者的偏好排序通过某种方式汇总以确定最终获胜者。十八世纪法国思想家孔多塞(Condorcet)提出著名的关于民主排序表决的“投票悖论”[2]。有甲乙丙3人对3个备选项a、b、c进行投票排序, 其投票结果为： 群体偏好a高于b、 偏好b高于c、偏好c高于a, 显然这种所谓的“群体偏好次序”存在内在的矛盾。从传递性的个体偏好出发, 按照少数服从多数的原则, 却得到非传递性的群体偏好, 这就是典型的孔多塞悖论。后来肯尼斯·约瑟夫·阿罗(Kenneth J．Arrow)对悖论进行数学论证, 并在1951年提出阿罗不可能定理： 在3个或更多的备选项情况下, 任何多于2人参与的表决系统都不可能同时满足4条准则： 无限制域准则(每个人都能按照其偏好对备选项进行排名)、 无关选择的独立性(只要所有人对a和b的偏好不变, 不管对a和c或其他备选项的偏好如何变化, 则社会对a和b的偏好不变)、 帕累托法则(如果所有人都偏好a高于b, 则社会也偏好a高于b)、 非独裁性(社会偏好不被1个人或少数人的偏好所决定)。

投票是表达个人偏好的手段, 没有基本事实, 对存在基本事实的排序聚合问题, Steyvers等[3]提出基于瑟斯顿方法和马洛斯方法的概率模型, 对存在基本事实的排序问题进行研究, 这两个模型虽然提取出群体的排序, 并表示出与这个排序相关联的不确定性, 但这两个模型并没有完胜启发式聚合方法。笔者在借鉴前人研究的基础上, 引进6种不同的聚合方法进行比较, 以期在这6种方法中找到群体智慧最佳排序聚合方法, 但缺点在于也许还存在另外还没被研究发现的更佳的聚合方法。

两个排序之间偏差距离计算的传统方法为肯德尔τ秩相关测度法, 用以测量两个长度相等排序之间的相关性, 是使用较为广泛的经典测度方法, 公式为

(1)

肯德尔τ秩中存在一个尚未解决的问题, 就是仅使用了简单的计数值nc和nd对两个个体排序间的不吻合之处加以惩罚, 未考虑到这些不吻合之处出现的相对位置造成的影响, 即默认排序排在靠后和靠前位置上的不一致性所造成的影响相同。而在现实排序中, 排在不同位置的影响往往不一样, 比如在某个多选项排序问题中, 其中两个选项分别被排在第1、 最末和分别被排在第1、 第2对于排序的总体影响是不一样的, 运用肯德尔τ秩计算时这两种排法都被识别为排名顺序一致的选项对, 没有体现出差别。故笔者在计算排序之间距离时使用一种更为严谨的测量方法即加权简捷测度法, 此法给予不同位置选项对相应的加权值以体现出排序的差别[4-6]。笔者使用新颖的加权偏差距离测量方法对排序之间的偏差进行计算, 定义群体智慧测量指标的概念, 并探讨现有排序任务问题群体智慧中的最佳聚合方法, 为群体智慧的研究以及排序任务问题的聚合策略提供参考意义。

1 实 验

1.1 实验操作

进行两个实验测试, 测试1的群体是华南地区某高校80名MBA硕士, 测试2的群体是华南地区某高校77名在校大学生, 测试题目如表1所示。排序测试问题有1个已知的基本事实答案, 测试1中各城市人口数量采自《中国产业信息网》上公布的官方统计数据, 真实排序为4-6-1-3-5-2； 测试2中6种类型的死亡人数数据采自《国家统计局》, 根据统计数据得到的真实排序为3-6-2-4-1-5。为保证每个参与者的排序答案都是独立且分散的, 在实验测试中不允许个体之间进行沟通交流和查阅资料, 仅限独立完成。测试前告知受试者作答最接近真实答案的个人将获得奖品, 激励他们认真思考作答。

表1 测试题目

合理控制受试者的作答时间在90 s左右, 避免由于时间过短导致受试者胡乱填写, 也避免作答完成后受试者之间的交头接耳。测试1总共派发80份答卷, 回收79份, 其中2份无效(一份的回答中有两个选项的排序数字相同, 另一份字迹模糊不清), 有效答卷为77份。测试2总共派发77份答卷, 回收77份, 全部有效。由于MBA学员来自不同的地方， 从事不同的工作, 学生来自全国各地, 在严格控制实验环境的条件下, 实验测试符合群体智慧发生所要满足的多样化、 独立性和分散化条件。

1.2 实验数据

两次测试回收的数据总体情况如表2和表3所示。测试1中排位标准偏差最大的为洛阳, 在6个城市中洛阳的人数真实排位在第6, 而真实排位在另一端的第1的苏州标准偏差比洛阳小, 说明受试者对洛阳人数排位猜测的差异性比苏州的大, 并反映出群体对于洛阳人数排位的不确定性最大, 排位标准差最小的青岛人数排位最集中。测试2中各选项排位标准偏差相差不远, 说明各选项排位比较集中, 意见差异性比较小。

表2 测试1统计量

表3 测试2统计量

排序数据的具体情况如图1和图2所示。测试1的各选项在1～6各个排位上都有出现。相比其他城市, 多数人把长沙放在第1或第2、 把洛阳放在第6的排位, 说明这个群体中大多数个体认为长沙城市人口最多, 洛阳城市人口最少, 事实确实是洛阳人口最少, 而长沙人口仅高于洛阳。

测试2中受试者对艾滋病死亡人数排位猜测比较集中, 多数人把其排在末几位, 人们对这个危害性极大的传染病情况了解比较相近。受试者给出的排位最一致的是对交通事故死亡人数, 把其排在第1位的人数超过了一半, 真实排位在第1和第2的脑血管疾病和火灾却被大大低估了。

图1 测试1各选项的频率分布直方图

图2 测试2各选项的频率分布直方图

在数据处理中发现无论是测试1还是测试2, 都没有1个个体排序与真实排序完全一致, 说明多选项排序题目的难度比较大。在测试的结果中可以看到排序的每个选项都有被排在正确的和错误的位置, 则如果利用不同的聚合方法把这些个体的排序聚合成一个群体的排序, 会产生怎样的效果, 不同的聚合方法得到的群体排序又是否相同, 下面将详细阐述不同的聚合方法及其应用到测试数据中的表现。

2 群体智慧效度

群体智慧是指由组成群体中的个体贡献自身的知识、 技能和经验, 将其转化为群体的并优于大部分个体的现象[7]。詹姆斯[8]提出在适当的环境下, 团体在智力上表现非常突出, 而且通常比团体中最聪明的人还要聪明； 即使有个别团体中绝大多数人都不是特别地见多识广或富有理性, 但仍能做出一个体现出集体智慧的决定。他总结了群体智慧发挥作用的条件： 观点的多样性(人们各自拥有不完全相同的知识和信息)、 决策的独立性(人们的观点不受周围人的意见所左右)、 权力分散化(人们依赖自己拥有的信息知识作答)、 集中化机制(将个体判断聚合为群体判断的机制)[9-11]。

关于群体智慧的定量测量指标, 尚未有准确定义, 笔者创新性定义评估群体智慧的概念----群体智慧效度, 并统一计算群体智慧效度的方法, 使群体智慧抽象概念得以量化研究。

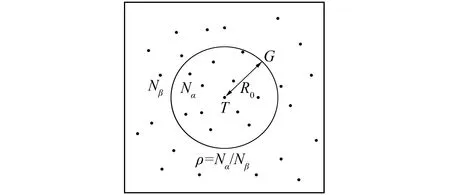
图3 群体智慧效度定义图

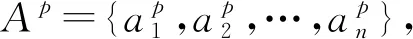
定理1 当0≤ρ<1, 则群体智慧存在；ρ→0, 群体智慧效应越显著。0≤ρ≤0.5时, 群体智慧为强效应； 0.5<ρ<1时, 群体智慧为弱效应。

在定义1里涉及测量排序之间偏差距离的方法为加权简捷测度法[12-13]。偏差值Rp由两个排序之间的距离除以不一致性在排序中出现位置进行相应惩罚的加权值得到, 计算公式为

(2)

其中1(i)为选项i在排序1中的排名, 1′(i)为选项i在排序1′中的排名, 分母为选项i在两个排序中排名靠前的排名位数(在两个排名中取小值)。1≤min{1(i),1′(i)}≤n,Rp≥1, 因此测度值越小, 两个排序就越接近。

3 聚合方法及应用比较分析

集中化机制作为群体智慧发挥作用的前提条件, 其作用十分重要。若没把群体里零散个体的信息汇聚成群体总信息的机制, 则无法考量群体与个人的关系, 更别提测量群体智慧的强度。笔者使用以下6种排序聚合方法对排序测试数据进行聚合比较。

3.1 中位数法

这里的中位数是指把选项排位的频率分布直方图分成两个面积相等的平行于Y轴的直线横坐标, 满足公式P(X≤x)=1/2。求出各个选项排位频率分布直方图的中位数, 并进行升序排序即可得到各选项的群体排序。

3.2 众数法

构建位置次数矩阵N=niL,niL为i选项被排在第L个位置的所有个体的数量,i1L1为第1个被确定的i选项和L位置,imLm为第m个被确定的i选项和位置L。排序时最大元素矩阵Max1niL=1,Max2niL=2, (其中Max1niL=1所在的行和列元素∉niL)；Max3niL=3, (其中Max1niL=1、Max2niL所在的行和列元素∉niL), 以此类推, 即可得到对应的群体排序。

3.3 Kemeny-Young方法

构建个体排序距离矩阵R=RP,RP为个体排序两两之间的偏差距离, 矩阵R的所有行和最小数所对应的个体排序即作为群体排序

(3)

3.4 波达记数法

构建排序位置矩阵L=LPi,LPi为个体p把选项i排在L的位置。根据L的列和进行升序排序即可得到各选项的群体排序

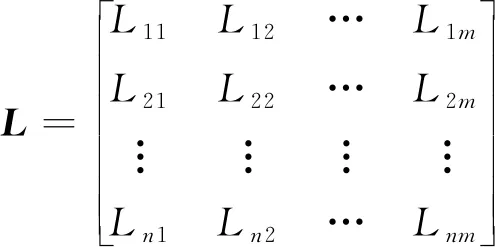
(4)

3.5 模拟比赛法

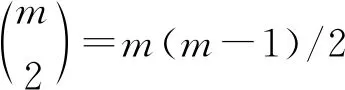
3.6 图论法

图4 图论方法原理

图4为图论方法原理。 由图4可见, 每个选项分别对应图中1个节点, 箭头指出为出链, 指入为入链。各边的权值Wij与Wji来自所有个体排序,Wij为选项i排名在选项j之后个体排序中两者名次差的总和,Wji为选项j排名在选项i之后个体排序中两者名次差的总和,i≠j。括号里面的数值为Wij与Wji的归一化数据, 对图上的归一化数据使用PageRank法(一种节点排名方法), 便得到一个PageRank向量, 最后根据此向量进行降序排序, 即可得到各选项的群体排序。

3.7 约束条件法

令常量cij=(i的排名在j之前的排名数量)-(i的排名在j之后的排名数量), 得到一个n×n的斜对称矩阵C。矩阵C是由衡量一致性的常量构成, 然后是产生这n个选项的排名, 使一致性达到最大, 故定义决策变量

(5)

最后的聚合排名对应矩阵X, 把X矩阵的列和进行升序排序, 便得到选项的排名。最优化问题： 希望最大化输入列表之间的一致性, 用常量和变量表示为

(6)

约束条件：

1) 对所有不同的对象对(i,j), 有Xij+Xji=1(反对称性)；

2) 对所有不同的三元组(i,j,k), 有Xij+Xjk+Xki≤2(传递性)；

3)Xij≥0(连续形式)。

上述为完整的二值整数线性规划问题(BILP： Binary Integer Lnear Pogramming), 实质是对孔多塞悖论的一个解决方法, 在孔多塞方法的基础上定义常量和变量, 添加约束条件, 使最后的聚合结果不可能出现悖论。

3.8 聚合方法比较分析

根据前面7种排序聚合方法和群体智慧效度概念对实验测试的数据进行处理得到结果分别如表4和表5所示。表4、 表5中给出了测试的真实排序以及利用不同聚合方法得到的对应群体排序,RP为群体排序与真实排序之间的偏差距离, 排位百分比(%)表示RP在所有个体排序与真实排序之间的偏差距离中的排位, 百分比越低, 表示排位越高。ρ为群体排序表现出的群体智慧效度。

表4 测试1各种聚合方法的表现

在表4中7种聚合方法表现里, 图论法的表现最差, 得到的群体排序的排位百分比在54.55%, 落后于群体中超过一半的个体,ρ=1.2>1没有表现出群体智慧。波达计数法、 模拟比赛法以及约束条件法得到的群体排序相同, 0.5<ρ=0.71<1, 表现出的群体智慧为弱效应。K-Y方法表现稍好于前者, 同为群体智慧弱效应。中位数法和众数法得到的群体智慧排序偏差距离最小,ρ=0.17≤0.5表现出群体智慧强效应。

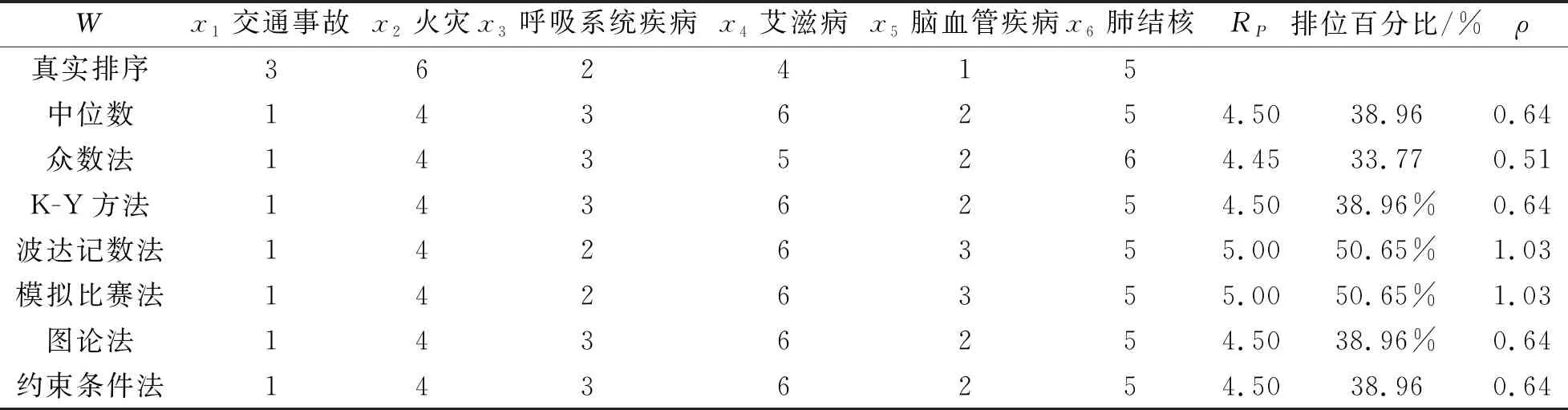
表5 测试2各种聚合方法的表现

表5中各种聚合方法的表现比较相近, 偏差距离RP均在4.45～5范围内, 在表5中可以发现, 虽然RP=0.45的4个聚合方法与RP=5的波达计数法、 模拟比赛法仅相差了0.5, 但是却表现出完全不同的效果。前者表现出群体智慧弱效应, 后者没有表现出群体智慧效应, 说明此次测试的受试者作出的个体排序与真实排序的偏差距离一致性程度比较高, 出现不少偏差距离相同的情况。在此次测试中表现最好的仍然是众数法ρ=0.51, 虽然是弱效应, 但与强效应相近。

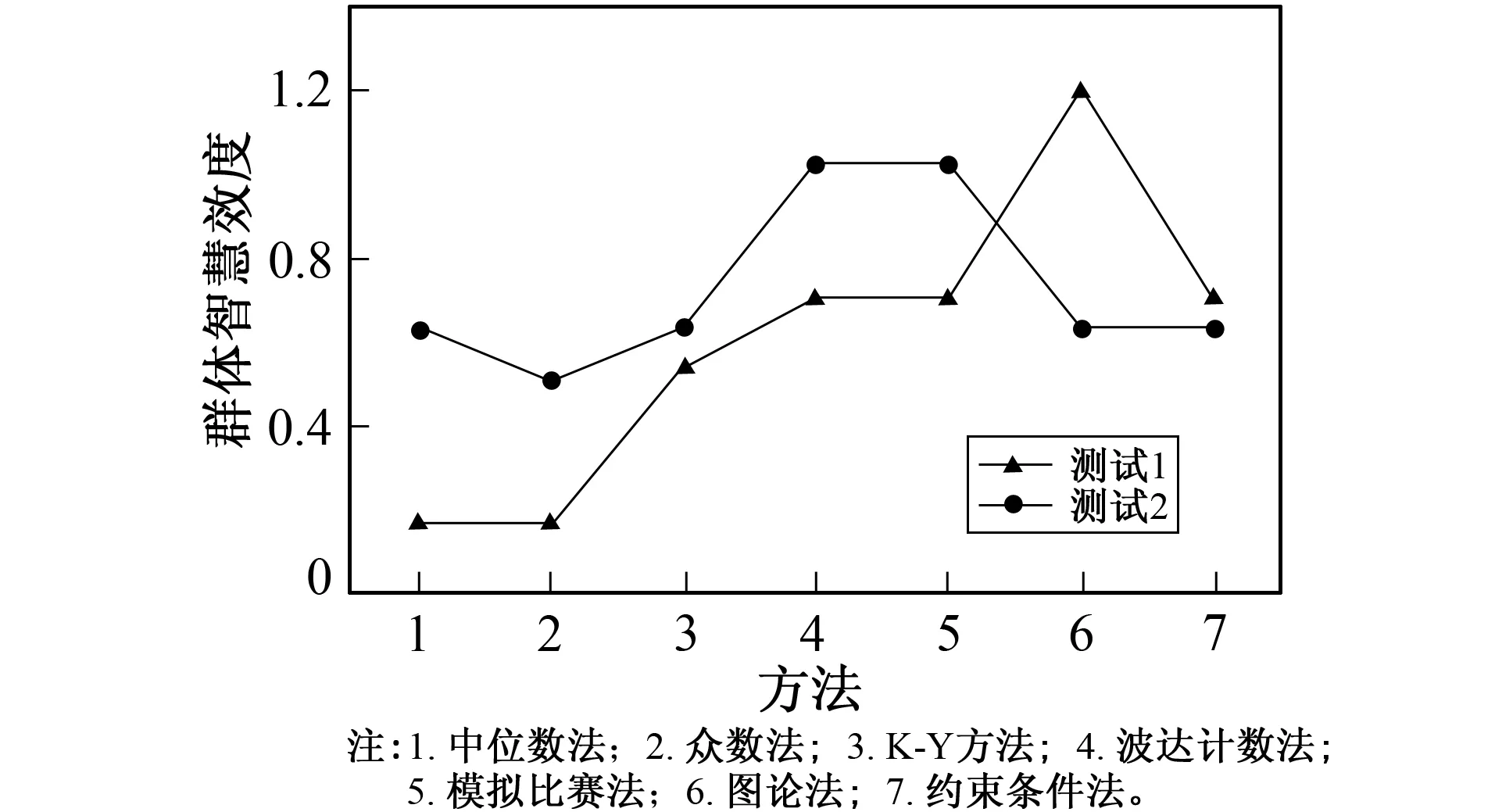
图5 不同聚合方法群体智慧效度比较

将两次测试的群体智慧效度整合成折线图如图5所示。从图5中可以看出, 在同一个测试中, 使用不同排序聚合方法得到的群体智慧效度不尽相同, 即使在一个测试里表现相同的方法在另一个测试里的表现也不相同, 只有波达计数法和模拟比赛法在两次测试里都有着相同的表现, 说明这两种聚合方法的效果类似。不过相比其他方法, 这两种方法得到的群体智慧效度比较高, 在表现上较差一些。众数法的表现是最好的, 在两个测试里都得出了最低的群体智慧效度, 其次是中位数法和K-Y方法, 图论法和约束条件法表现一般且不太稳定。

4 结 语

笔者在群体智慧背景下, 对排序任务问题的7种排序聚合方法进行比较研究, 找到其中使排序任务问题群体智慧效应最显著的排序聚合方法。并定义了群体智慧测量指标的概念----群体智慧效度ρ, 以定量分析群体智慧效应的强度。当0≤ρ<1, 则群体智慧存在；ρ→0, 群体智慧效应越显著, 0≤ρ≤0.5时, 群体智慧为强效应； 0.5<ρ<1时, 群体智慧为弱效应。做出两个实验测试收集群体对于排序任务的选项排位数据, 对数据使用7种排序聚合方法进行处理, 最后得到对应的群体智慧效度。比较结果显示, 在排序任务问题下, 通过对不同排序聚合方法得到的群体智慧效度的比较发现, 众数法的表现最好, 中位数法和K-Y方法稍弱于众数法, 波达计数法和模拟比较法表现相似皆为一般, 孔多塞悖论的改进方法----约束条件法虽然与个体排序的一致性程度最高, 但其表现也是一般, 图论法的表现较差且不稳定。目前使用最广泛的排序聚合方法为波达计数法, 而笔者通过对7种排序聚合方法比较分析, 找到对于已知事实的排序任务问题群体智慧效应的研究中比波达计数法的表现更好的方法----众数法, 此研究结果为后者进行排序任务问题的群体智慧相关研究作出参考价值, 也为各个领域设计寻求群体智慧涉及排序聚合的工作(比如决策排序、 预测排序等)作出一定的贡献。