基于负半熵 下半方差 近似偏度的投资组合模型及应用

欧 攀，王 沁，段静静，周文浩

（西南交通大学数学学院，成都 611756）

在全球经济一体化的推进下，中国金融市场的波动日益加剧，金融风险也随之不断增加，因此对金融市场风险进行度量和控制是非常有必要的。1952年Markowitz［1］以投资组合收益率的方差作为风险度量，提出了均值方差投资组合模型（mean variance portfolio model，M-V），开创了投资组合量化风险的先例。我国证券市场历史较短，存在不成熟性和多变性，如何在一定约束条件下得到最优投资决策，进一步修正M-V模型，使其应用于我国证券市场，这在理论研究和实际应用中都有重要意义。

均值 方差模型中方差作为风险度量指标，既包含收益向下的波动，也包含向上的波动。而投资者在实际投资时，更关心资产收益低于预期收益的那部分风险，因此提出了下半方差风险度量方法。J.Bi［2］给出了均值半方差投资组合模型；Rui Pedro Brito［3］提出了下半方差和偏度双目标优化的投资组合模型；Yan W［4］考虑在多期情况下建立了多周期下半方差投资组合模型；王延章［5］构建了下半方差的债券投资组合模型；李慧敏［6］构建了下半方差的地产投资组合模型。半方差模型中下半方差度量风险，只说明了收益率的偏离方向，而未反映证券组合的损失具体大小。信息熵也代表一种不确定性，风险的本质是回报的不确定性。近年来很多学者考虑用信息熵度量资产风险，Philippatos［7］首先将熵引入投资组合模型，用熵代替方差度量风险。其后，更多学者用熵作为风险度量方法，其中，王灿杰［8］建立了均值熵偏度模型；YU J R［9］在熵模型的基础上增加收益预测；张鹏［10］构建了具有熵约束的组合投资模型；吴文娣［11］建立了具有广义熵约束的投资组合模型；李爱忠［12］、Mehmet Aksaraylı［13］、宋燕玲［14］同时考虑方差和信息熵风险度量指标，构建了均值方差熵投资组合模型。

综上所述，国内外学者分别用方差、下半方差、信息熵度量组合资产风险，修正了均值方差模型，建立了多种投资组合模型。本文结合投资者更关注资产收益处于下跌的心理和信息熵的优点，构建了负半熵—下半方差 近似偏度投资组合模型，互补了这些方法单独度量风险时存在的一些缺陷，使模型更具有效性和可行性。

1 模型的建立

1.1 M-V投资组合模型

M-V投资组合模型用方差度量风险，期望度量收益，在同时考虑资产风险和收益中寻找一种平衡。假设现有n种风险资产，rj表示第j（j=1，…，n）种风险资产的收益率，wj表示第j种风险资产的投资权重（其中n），则组合资产收益率为rp=w1r1+w2r2+…+wnrn。期望收益率、方差风险分别为：

式（1）～（2）中：投资权重向量 w=（w1，w2，…，wn）T；资产收益率向量 r=（r1，r2，…，rn）T；协方差矩阵 Q=（σij）n×n（其中 σij=cov（ri，rj））。

根据式（1）与式（2）可见，当确定了投资权重向量w，组合资产的收益和风险也就确定了。记e=（1，1，…，1）T，参数 r0为预设最小收益率，则M-V投资组合模型如下：

1.2下半方差—近似偏度投资组合模型

资产风险既包含了资产收益高于期望收益的风险，也包含了低于期望收益的风险。而投资者在实际投资时，更关心资产期望收益低于投资者预期收益水平的风险。这样一来，提出了下半方差（lower semi-variance，SV）的概念。如果 SV（rj）=E［（min（rj-Erj，0）2］＜+∞，那么，第 j种风险资产的下半方差定义为：

假设除节假日外的n种风险资产，在一段连续时间内，第 j（j=1，…，n）种资产在第 t（t=1，…，T）天的收益率为rtj，那么第j种风险资产的期望收益率矩估计为，方差、下半方差的矩估计分别为：

偏度衡量了资产收益率分布的不对称，当偏度大于0时，意味着资产收益率大于期望的概率大一些，风险相对小一些。第j种风险资产的偏度Skew（rj）=E［rj-Erj］3，因正态分布的偏度为 0，方差和下半方差比值为2，考虑用方差和下半方差比值与2的差值近似偏度。那么根据式（4）与式（5）得到第j种风险资产的近似偏度矩估计为，由式（6）与式（7）得到 n种风险资产组合的近似偏度矩估计为：

以资产组合的下半方差为目标函数，在M-V模型约束条件上引入偏度系数大于0，得到半方差—近似偏度模型（semi-variance approximate skewness model，SVASM）。那么，SVASM模型可以表示为：

1.3负半熵—下半方差—近似偏度投资组合模型

风险本质上是资产收益率的不确定性。信息熵是系统的无序程度与信息量的有效结合，信息熵数值越小，样本不确定性程度就越小。相比只能反映分布二阶矩特征的方差，信息熵能更加准确度量组合资产的全部风险。假设X是离散型随机变量，其概率分布律为 pi=P（X=xi），pi≥0，i=1，…，n，那么，信息熵为如果X是连续型随机变量，M.Rao［15］给出了一种新的信息度量方法——累积剩余熵，其表达式为：

对于投资者而言，更加在乎组合资产收益低于期望收益的信息。这样一来，根据式（9）提出负半熵（negative half entropy，简称 NE）的概念。负半熵公式为：

负半熵本质是一种期望，它衡量了组合资产收益低于期望收益的信息。基于频率代替概率的思想，可以获得组合资产负半熵的矩估计，步骤如下：

步骤1 将第j种风险资产在第t天的收益率rtj减去样本均值 ¯rj，获得新序列 ytj=rtj-¯rj；

步骤2 将新序列ytj分成长度相等的m个子区间，记载每个子区间中新序列ytj小于0的频数Nij（i=1，…，m，j=1，…，n）；

步骤3 用频率估计概率的方法，获得收益率序列 ytj落在第 i（i=1，…，m）个区间上的概率

步骤5 权重向量为 w=（w1，…，wn）的组合资产收益的负半熵为

下半方差常常受资产变量分布的影响，因而用负半熵补偿下半方差度量组合资产收益低于期望收益的那部分风险，这样一来，在SVASM模型基础上，构建负半熵 —下半方差 —近似偏度模型（negative half entropy lower semi-variance approximate skewness portfolio model，NESVASM）为：

其中 λ为调节参数［16］，需满足 λ＞0；H^-（w）表示n种风险资产组合的负半熵。

2 实证分析

2.1 数据的选取与处理

在实际投资组合中投资资本有限，投资者在考虑选取资产时，既要兼顾分散风险又要考虑自身资本承受能力，因此投资组合中的资产数量不宜过多。根据投资组合原理以及对中国金融市场调查研究得出的经验法则，当投资组合中证券数量过多时，组合对非系统风险的分散作用开始减弱。因此，在组合投资时选择13种风险资产，此时对非系统风险的分散作用较大。从泸深300中，涉及银行、通信、建筑等多个行业选择相对平稳的13只股票进行研究，所选股票见表1。为保证模型的时效性，选取2016年3月1日至2017年3月1日，除节假日外的日收盘价进行实证分析。假设第j只股票在第t天的收盘价为stj，则收益率为rtj=ln stj-ln s（t-1）j，t=1，…，T，j=1，…，n。

2.2 描述性分析

根据定义，计算出各只股票的样本均值与方差、下半方差与负半熵、样本偏度与近似偏度，如表2所示。

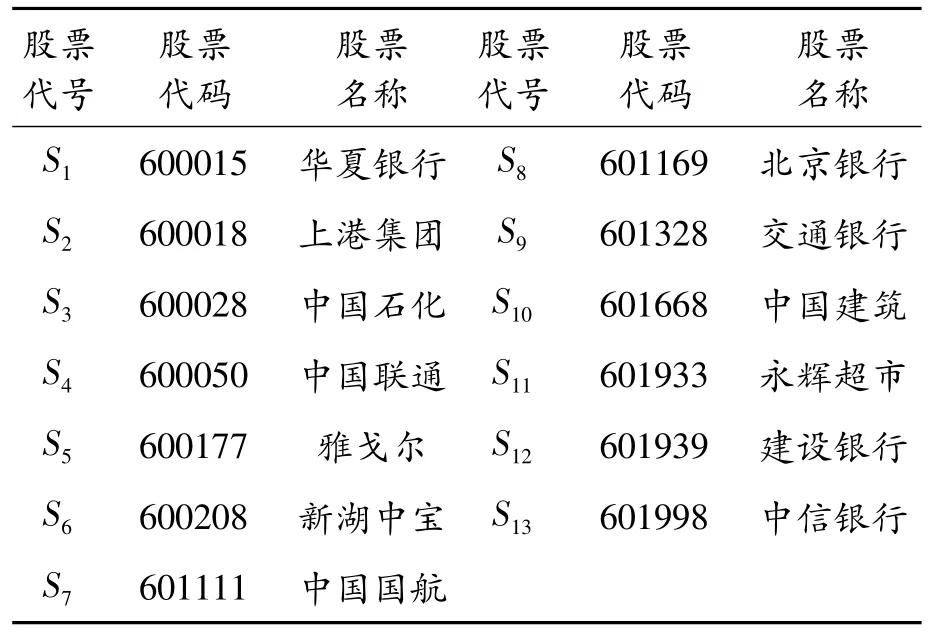
表1 选取的13只股票

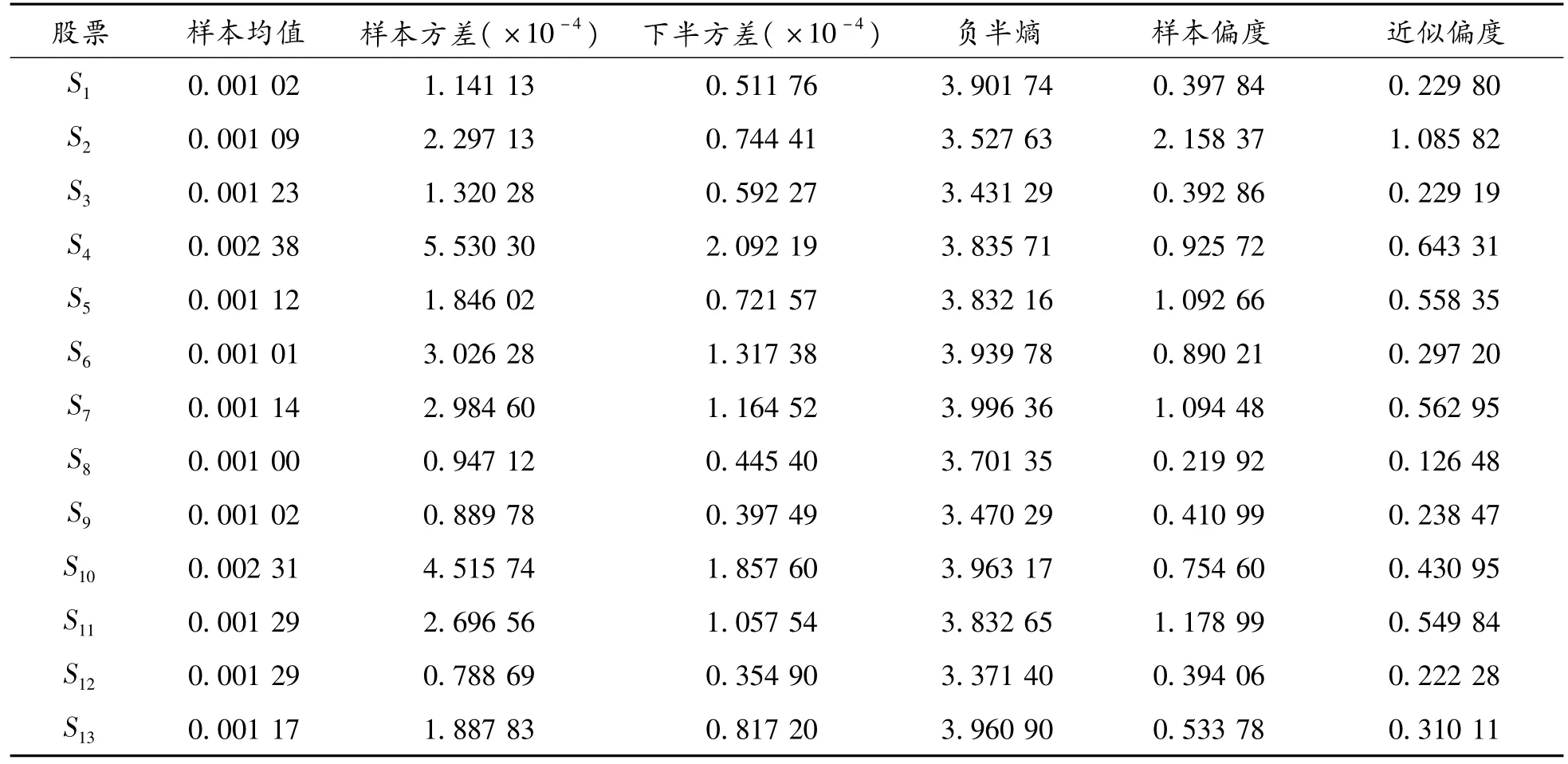
表2 各只股票的样本均值与方差、下半方差与负半熵、样本偏度与近似偏度

从表2可以看出：①在13只股票中，股票S2、S4的下半方差比其方差要小得多，可见下半方差在方差中并非对称的，用下半方差度量风险能更加准确地度量股票收益向下波动的那部分风险；②负半熵与下半方差进行比较，13只股票的负半熵与下半方差有大致相同的增减趋势，这与负半熵和下半方差都是度量低于期望收益风险相吻合；③近似偏度与样本偏度进行比较，股票S2和S8是样本偏度值中最大和最小的2只股票，在近似偏度值中股票S2和S8同样是最大和最小的2只股票，并且近似偏度与样本偏度有几乎一样的大小趋势，这表明近似偏度与真实偏度存在较好的拟合效果。

2.3 模型NESVASM的求解

根据拉格朗日乘子法和梯度下降法对模型进行编程求解，模型NESVASM中存在调节参数λ和收益参数r0，图1给出了模型在相同收益参数、不同调节参数下，13只股票的投资组合情况。

从图1可以看出：①模型求解的投资权重wj分布在第 2、3、8、9、11、12只股票，没有呈现集中分布现象，符合分散投资理念；②随着调节参数λ的逐渐增大，负半熵的作用逐渐显现，负半熵更小的股票S9和S12投资权重呈增加的趋势，负半熵更大的股票S8和S11的投资权重呈减小的趋势，这也表明用负半熵来衡量风险时，股票S8和S11被度量出了更多的风险，模型更看好股票S9和S12。

图2给出了模型在相同调节参数、不同收益参数下，13只股票的投资组合情况。

从图2可以看出：①随着收益参数r0的逐渐增大，呈现股票 S4、S10替代股票 S2、S3、S8、S11的现象，可见股票S4和S10发生超额收益的可能性更大；②调节参数也可看作投资者对负半熵的偏好程度，不同投资者对风险偏好和收益要求不同，调节参数和收益参数可根据实际情况进行适当调整。

表3给出了在不同调节参数λ和收益参数r0下NESVASM模型的收益率、下半方差、负半熵、近似偏度值。

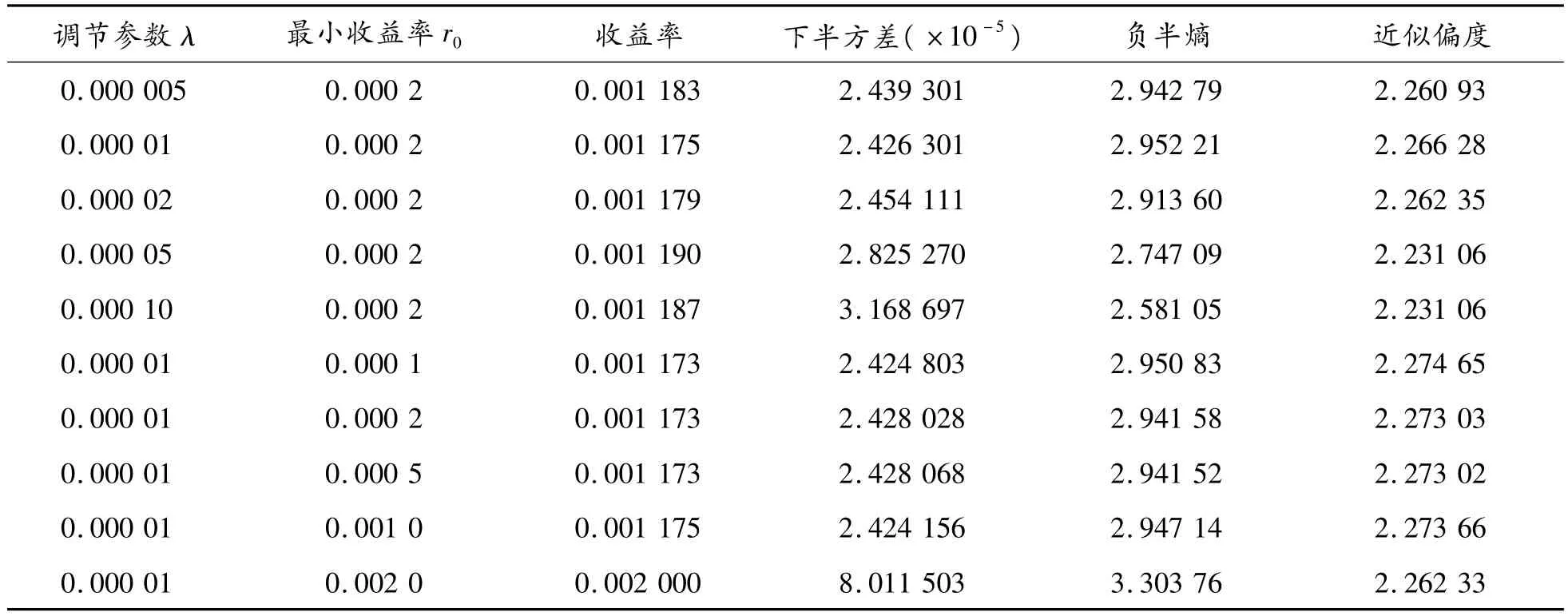
表3 NESVASM模型在不同调节参数λ和收益参数r0下的结果

从表3可以看出：① 在固定收益参数r0时，随着调节参数λ的逐渐增大，下半方差呈增长趋势，负半熵呈减小趋势，这与负半熵在目标函数中比例变大相吻合；② 同样，在相同收益参数r0条件下，NESVASM模型在λ=0.000 01时，负半熵比在λ=0.000 005时的负半熵更大，表明此时负半熵度量出了更多的高阶矩风险，使得本应更小的负半熵出现变大的现象；③ 在固定调节参数λ条件下，随着收益参数r0的增大，下半方差和负半熵呈增大的趋势，这与收益更大风险更大相吻合。

2.4 模型NESVASM与MV模型、SVASM模型的比较

为进一步说明负半熵对投资组合的影响，取定模型NESVASM中参数λ=0.000 01，r0=0.000 2，与M-V、SVASM模型的投资权重进行比较，结果见表4。

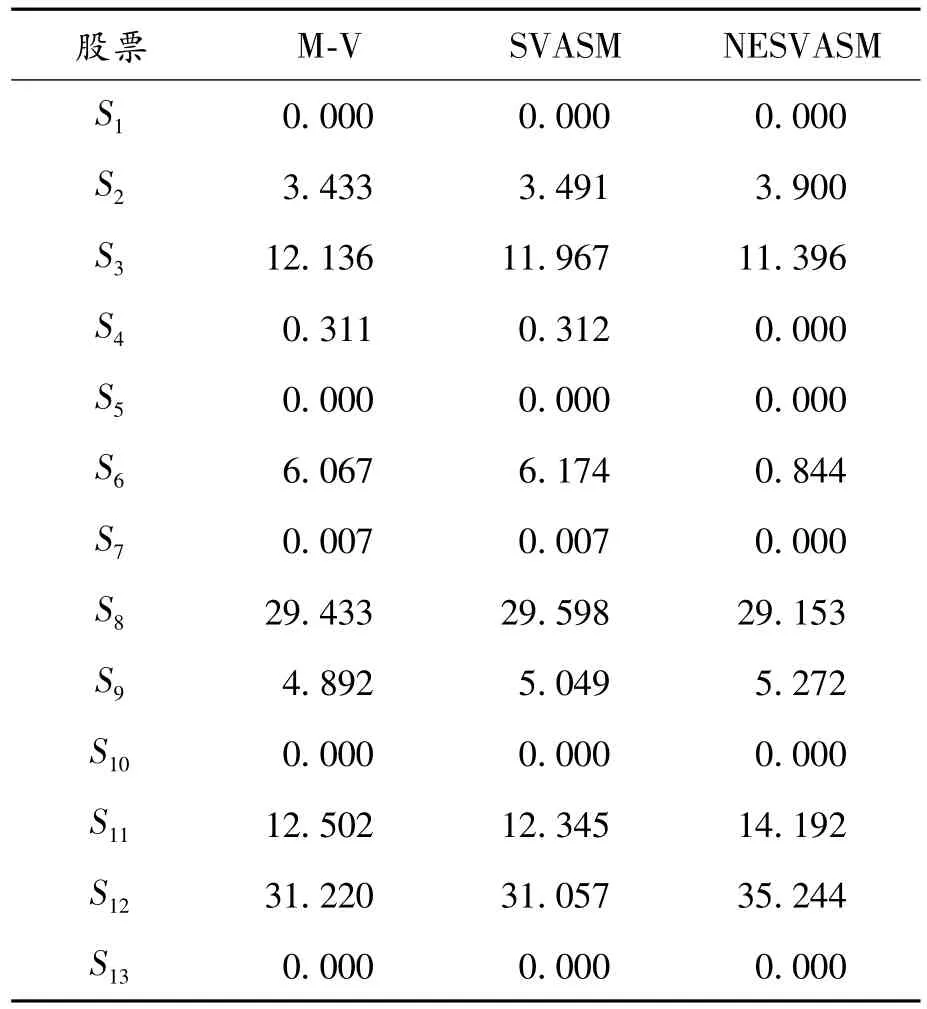
表4 在3种不同模型下的权重情况 %

从表4可以看出：① 与SVASM模型比较，NESVASM模型中股票S3、S6、S8的权重比例有所减小，股票 S2、S9、S11、S12的权重比例有所增加，这可能是负半熵度量出了股票S3、S6、S8的下半方差风险外其他高阶矩风险所导致的结果；②特别是在股票S6、S11、S12上的权重比例存在明显的变化，为投资者进行选股时给予更多理性参考。

通过计算得到3种模型下的收益率、下半方差、负半熵、近似偏度，结果见表5。

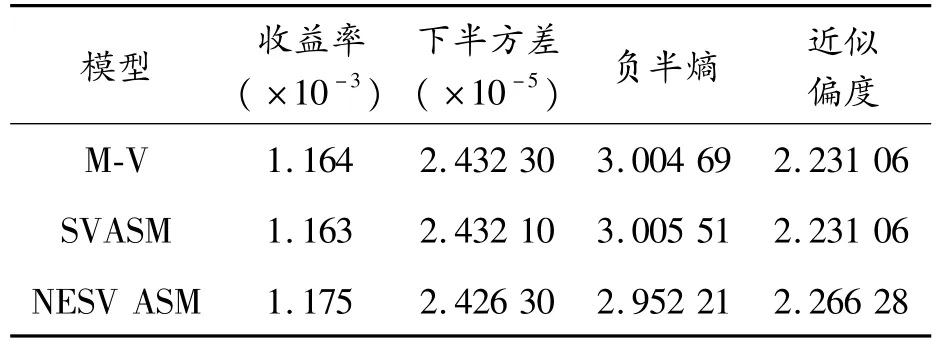
表5 M-V、SVASM、NESVASM模型的结果

从表5可以看出：与M-V、SVASM模型相比，模型NESVASM收益更大，风险度量指标中下半方差和负半熵均更小，并且组合资产偏度也存在明显提升。可见，结合负半熵的NESVASM模型更能反映组合资产所面临的风险，能更有效地规避风险，为投资者在配置资产时提供更加合理的选择。

3 结论

在传统M-V模型的基础上，考虑到投资者更关心资产收益能否达到预期收益的心理，通过用负半熵补偿下半方差衡量资产收益低于预期收益的风险，并在约束条件中引入偏度系数，构建NESVASM模型。通过选取13只股票进行实证分析，发现NESVASM模型能获得更大的收益，能更好地规避风险，并且发生超额收益的可能性更大。在理论上，结合负半熵与半方差度量风险的NESVASM模型，规避了它们单独度量风险存在的缺陷；在实际投资时，NESVASM模型从方差和信息熵的角度度量资产收益低于预期收益风险，给风险厌恶型投资者更多的理性指导，在股票选择和风险预测方面也具有指导意义。此外，模型约束条件也可考虑引入正半熵大于负半熵，本文中实证分析也可考虑期货、期权、债权等衍生产品或流动性因素，使模型更加切合真实的金融市场。