基于改进集束搜索的立体车库库位布局优化研究

常立丹，李建国，李博文

（兰州交通大学自动化与电气工程学院，兰州 730070）

自动化立体车库在解决城市静态交通问题方面起着越来越重要的作用，汽车保有量的日益增长和土地资源的稀缺更推动了自动化立体车库的发展。与此同时，自动化立体车库的出现在一定程度上缩短了车辆的存取时间，降低了资源的浪费。但其也存在一定的局限性，例如存取车效率较低、顾客等待时间长和运行能耗较高等问题。

目前，对自动化立体仓库的研究较多且较全面，在考虑仓储系统内部搬运器与升降机调度问题时，主要将车辆存取过程抽象为旅行售货员问题（travel salesmen problem，TSP）［1］。采用遗传算法［2］、多目标集成优化［3］、系统智能预测［4］对立体仓储系统进行调度分析。

对于立体车库调度优化的研究，吕洪柱等［5］针对大型立体停车库存取车控制问题，设计了一种智能存取车控制算法，解决了多台车辆同时存取的经济效益权衡和安全问题。陈博等［6］通过改机遗传算法对堆垛机运行路径进行了优化。丁彩虹等［7］采用PLC对车库系统进行控制操作。

针对寻找最优路径的研究，李建国等以堆垛机运行最短路径为目标，建立了堆垛机复合作业和单一作业的数学模型，利用改进遗传算法对存取车序列进行优化，并与传统的存取车作业方式进行对比，结果取得了明显的效果［8］。李剑锋等［9］以总存取时间为目标函数建立了数学模型，利用改进遗传算法，采用混合编码、改良的OX交叉算子对车库存取序列进行优化，获得了预期的车辆存取优化序列。黄卫平等［10］以费用最小为目标，将集束搜索算法应用到随机型混合模式装配线平衡问题中，得到了较好的效果。罗晓冬等［11］采用Dijkstra算法并结合深度优先遍历算法筛选出任意2个节点间的所有最短路径，并找出花费代价最小的路径。

本文以北京市某立体车库实际运行数据为依据，以运行时间最短为目标，提出了一种改进集束搜索算法对立体车库堆垛机作业路径进行建模与优化，并对实验仿真结果进行分析，为立体车库选择合理的布局提供参考。

1 背景介绍

1.1 立体车库实体模型

立体车库主要由车厅、巷道、停车位、堆垛机和搬运器等组成，可以根据场地和高度的不同要求建成多种结构形式。立体车库本身是三维实体［12］，本文将堆垛机选择巷道的操作方向定为x轴方向，将堆垛机选择所要进行存取操作列的方向定为y轴方向，将选择所在层的操作方向定为z轴方向。

由于存取车作业是三维运动［13］，即在巷道内所进行一次存取车操作可分解为3个分方向上的运动：巷道方向上的水平运动X，用来选择巷道，并实现存取操作；垂直升降运动Z，即存取车位点所在的层j，用来选择车位所处的层；横向存取运动Y，即存取车位点所在的列i。对于不同的车位而言，X方向上的操作相同，因此可将模型简化为单巷道内（Y，Z）的二维运动，即寻找存取车位点（i，j）。由立体车库简化成的单巷道实体模型进行分析，将立体车库模型简化，取I/O口位置为坐标原点O，取选择存取位置所列的方向为i轴，取选择存取位置所在层的方向为j轴，取单侧车位进行分析，立体车库立体示意图如图1所示。

《车库建筑设计规范（2015）》规定，1个 I/O口对应约50个停车位，I/O口处应设置不少于2个的候车位，当I/O口分开设置时，候车位不应少于1个。考虑立体车库整体的造价，立体车库建造的最低层数为3层。堆垛机水平速度v1=80 m/min，垂直速度v2=20 m/min。车库车位的长L0=5 m，宽W0=2 m，高H0=1.8 m，但是规范中明显缺少了对车位如何进行布局的规定。

1.2 立体车库排队模型

排队论是一套主要研究系统随机聚散现象以及随机服务系统工作过程特点的数学理论和方法，通过对服务对象数量指标的统计，得出服务对象与服务系统之间存在的规律，并根据规律重新调整服务机构及组织服务对象，使得保证服务对象在满足需要的基础上服务系统的经济效益得到优化［14］。

结合北京市某医院自动化立体车库，它作为一个服务机构，到达的车辆可视为顾客，且车辆到达和服务时间均是随机的。根据排队论基本思想，可将立体车库存取车辆的过程看作1个排队系统，该系统主要由输入过程、服务机构和排队规则3部分组成，如图2所示。

自动化立体车库对车辆进行存取操作时，考虑复合作业方式。当对A车辆进行存储后，若B位置随即有出库任务，则堆垛机执行取车操作，即每次车库的作业方式为复合作业方式，如图3所示。若完成车辆入库后，无出库任务，则堆垛机返回出入口待命。

在车库排队系统中，其运行参考指标主要包括：

1）顾客到达率为λ，顾客服务率为μ；

2）整个车库系统中的顾客平均等待的队长Lq和等待时间Wq；

自动化立体车库有一个排队队列，有s个堆垛机参与存取任务，而且各个堆垛机之间相互独立，定义服务强度 ρs=λ/（sμ）。

则空闲概率P0为：

其中，a表示排队系统中有a个堆垛机正在参与服务，且0≤a＜s。

在排队系统中，只有当准备接收服务的车辆i大于堆垛机的数量s时，才会出现车辆排队等待，所以等待服务车辆的平均数为：

堆垛机将车辆A进行存储所需时间T1为：

堆垛机将车辆A进行存储后，随即对车辆B进行取车，所需时间T2为：

堆垛机将车辆B运送到出入口所需时间T3为：

则堆垛机在库内运行时间T为：

则系统运行时顾客的平均等待时间为：

其中，k表示停放车辆数，M表示车库停车位个数，i、j分别表示车库的列数和层数。

1.3 改进集束搜索算法

集束搜索算法（beam search algorithm，BSA）是一种启发式图搜索算法，其基本思想与分支定界法类似，但二者有一定的区别，主要表现在集束搜索算法不是对所有节点进行分支，为了减少节点搜索过程中所占用的空间和时间，在对每一个节点进行深度扩展时，对一些质量较差的节点进行裁剪，保留一些质量较高的节点。在搜索过程中对节点进行裁剪既节约了空间，又提高了效率。

针对一个搜索树，首先要确定一个叫束宽（beam width，bw）的参数。集束搜索首先根据某种准则，选择bw个最优的节点作为束节点（beam node）。如图4所示，第1层中的2个（bw=2）阴影节点，中间的那个节点就被忽略不计了，不再对其进行分支［15］。

对于每个束节点即阴影节点，以该节点作为搜索起始点，再进行分支，根据某种筛选规则对其子节点进行选择，将其中最优的一个节点作为束节点，而对其余节点不再进行分支。然后，再对选择的最优的节点进行分支，以此类推，直到叶节点。最后，得到bw个代表备选方案的束，对比不同的方案并选择最优的作为输出。

集束搜索方法其实提供了一种找最优解的思路，就是说在适当的情况下，可以剪掉一些可信度低的路径，在实际使用中，可以每层的集束宽度不一致，比如在初始的一些层次中多保留一些结果，在后边就可以放心大胆地进行剪枝。

由于传统集束搜索方法存在常数线宽大小影响求解效果的问题，因此本研究对传统集束搜索算法进行改进［16］，新算法的主要思路是将经典算法中的束进行分组，通过引入惩罚机制，使得每组的相似度尽量低，保证生成的解相互之间差异更大一些，即满足了多样性的需求，在每组束中用经典算法进行优化搜索。

2 立体车库库位布局分析

以北京市某医院自动化立体车库为例，该车库布局为4层7列双排对列布设，单巷道，单I/O口，堆垛机数量为1台。但在该配置及布局下，车库在实际运行过程中，尤其是存取车高峰期，存在排队过长、顾客等待和接收服务时间过长的现象。由此可以看出设备配置及库位布局会在一定程度上对立体车库的整体运行造成影响。因此，为保证立体车库具有较高的运行效率，在对立体车库进行设计时需考虑整体库位布局及合理数量的设备配置。本文将参考该立体车库的设备配置，讨论不同的车库布局对顾客平均等待时间及平均等待队长等因素的影响。

2.1 立体车库运行参数拟合

以该自动化立体车库实际运行数据为基础数据，截取1天24 h时即1 440 min内车辆到达时间，对车辆达到时间间隔进行统计分析，并进行到达概率拟合，如图5所示。

其中横坐标表示车辆到达时间间隔，纵坐标表示车辆到达时间段内的密度，对顾客到达时间进行概率拟合，得出顾客到达率分别服从参数λ为0.5辆/分钟的泊松分布。

2.2 改进集束搜索算法搜索最优路径

根据北京市某立体车库实体模型，将该车库的I/O口位置设为改进集束搜索的起始点，即根节点。采用改进集束搜索算法对堆垛机路径进行搜索选择时，首先将束按照临近搜索节点和远离搜索节点分为两组，每组均按照搜索当前距离L不大于2.5 m对路径进行搜索，即惩罚机制为当前搜索距离不大于2.5 m。

改进集束搜索步骤如下：

步骤1 在复合作业任务优先次序图中，生成可分配库位的集合；

步骤2 判断初始节点的数量N是否大于bw，若N＞bw，转向步骤3；若 N＜bw，则对初始节点进行分支；

步骤3 将不完整的分配通过某种派发规则转变成完整分配，并根据惩罚机制对分配进行分支；

步骤4 比较完整分配的目标值，并选择最优的bw个作为初始库位；

步骤5 对束节点进行分支，并计算节点的目标值，选择最优库位；

步骤6 从最终会产生的bw个完整的分配方案中选择最优的搜索的最佳库位。

3 仿真实验与分析

综合分析北京市某立体车库，得出该车库车辆到达时间服从参数为λ=0.5辆/min的泊松分布，车库服务率μ=0.9辆/min，在车库布局为4层7列双排对列布设，单巷道，单I/O口，堆垛机数量为1台的配置下，不同库位布局对整体运行效率产生影响。考虑整个立体车库的造价和安全性能等问题，设置车库的最低层数为3层，最高层数不超过9层，则该立体车库层数可设置为3、4、5、6、7或8层。考虑库容量约为50个，那么层数为3时，列数即设置为8列，此布局下该立体车库共有48个库位，符合约50个库位容量的要求。以此类推，得出不同层数所对应的列数，则可得出表1的立体车库层和列的不同组合。

表1 层和列不同情况的组合

针对上述7种层和列不同情况的组合进行模拟仿真，根据立体车库运行情况，设定束宽bw为4，就近存储规则，搜索最大层数为8层，惩罚机制为当前搜索距离不大于2.5 m，以S3为例，改进集束搜索算法搜索堆垛机路径示意图如图6所示。

采用Matlab进行仿真模拟对比，系统仿真流程如图7所示。

得出在北京市某医院自动化立体车库的配置设备下，不同库位布局下堆垛机作业路径长度、顾客的平均等待时间和平均等待队长，如表2所示。

从表2可以看出：改进集束搜索比集束搜索有较大的改进，堆垛机运行距离缩短约13%，顾客平均等待时间缩短约3.2%，平均等待队长缩短约18.7%。而且无论在任何方式下，S3情况即4层6列的库位布局顾客的平均等待时间、平均等待队长最短，堆垛机运行效率最高；随着层数变大，列数变小，顾客的平均等待时间、平均等待队长逐渐增加。

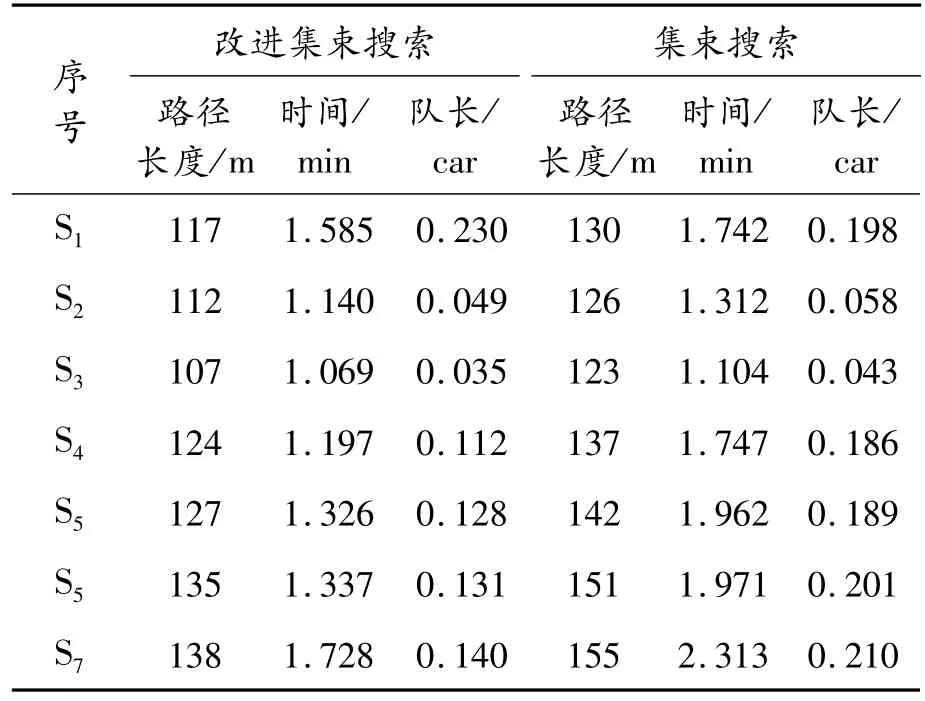
表2 改进集束搜索与集束搜索对比

4 结论

本文中以北京市某立体车库的实际运行数据为依据，提出了立体车库库位布局选择问题的集束搜索算法，并对此进行改进。首先给出集束搜索的路径选择原理过程，针对传统集束搜索方法存在常数线宽大小影响求解效果的问题，引入惩罚机制，对集束搜索进行了改进；然后将改进集束搜索应用到立体车库库位选择问题上，使用改进集束搜索算法对立体车库库位布局进行了优化。算例显示：本文中提出的改进集束搜索算法可以缩短堆垛机运行距离，提高立体车库运行效率，从而对立体车库的布局进行优化。