重叠组稀疏广义全变分图像去模糊方法
肖伟煌,陈颖频
(闽南师范大学物理与信息工程学院,福建 漳州 363000)
0 引言
图像在成像、转换过程中经常受到运动、光学仪器工艺、噪声等因素影响而造成图像降质。因此,图像去模糊是图像处理中的经典问题[1]。
文献[2]中广义全变分(total generalized variation,TGV)模型,对图像的高阶梯度进行稀疏约束,能有效去除阶梯效应,同时保存图像边缘及细节信息,是图像去模糊的重要工具。然而,传统TGV模型仅以L1范数对图像的梯度稀疏性进行刻画,没有充分挖掘图像梯度的邻域结构特性,不能有效刻画图像梯度的局部组稀疏先验,导致传统广义全变分模型在图像边缘保持和阶梯效应抑制能力有一定局限性[3]。
为了充分挖掘图像梯度的局部相似性,本文将一阶梯度和二阶梯度的邻域信息点进行重叠组合,将重叠组稀疏(overlapping group sparsity,OGS)理论[4-9]引入TGV模型,提出了基于重叠组稀疏收缩技术的改进广义全变分(total generalized variation based on overlapping group sparsity,TGV-OGS)图像去模糊模型。通过该模型进一步提高平滑区域与边界区域的差异性,保留图像边缘的有效信息,提高图像去模糊效果。
鉴于提出的图像重构模型较为复杂,计算量较大,本文引入带重启加速交替方向乘子(alternating direction method of multipliers,ADMM)方法[10-12]求解该模型,有效提高了图像去模糊算法收敛速度。
在后续实验中对比了几种图像去模糊方法,从实验结果可以看到,本文提出方法取得了最佳图像去模糊效果。
1 预备知识
1.1 二阶广义全变分去模糊模型
图像降质过程可理解为清晰图像和模糊核卷积运算后再加上噪声的结果[13],即:
G=H*F+N
(1)
式(1)中,G表示观察图像,H表示模糊核,F表示原始图像,N表示高斯噪声,*表示卷积算子。
二阶TGV模型不仅在去噪基础上发挥高阶变分优势,还在去模糊方法中有效地避免了阶梯效应,较好地保护图像边缘和细节部分,从而提高去模糊效果。
标准二阶TGV模型定义如式(2)所示[13]。
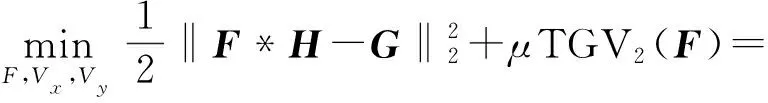
(2)
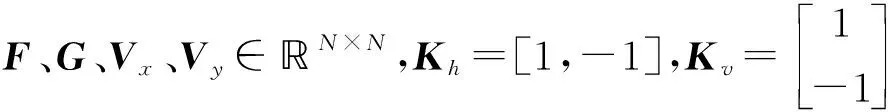
1.2 重叠组稀疏收缩算子
设V0为待收缩矩阵,可得其重叠组稀疏邻近算子记为[6]:
(3)
(4)
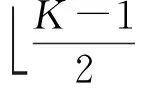
V(k+1)=mat{(I+γD2(V(k)))-1v0}
(5)
式(5)中,I∈N2×N2表示单位矩阵,v0是V0的向量形式,mat表示向量矩阵化算子,D(U)∈N2×N2是一个对角矩阵,其对角元素定义如下:
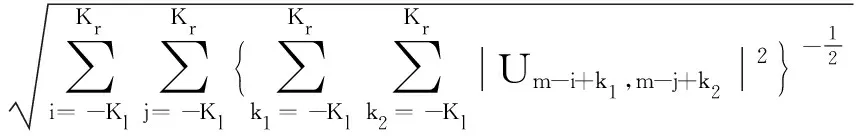
(6)
2 重叠组稀疏广义全变分图像去模糊方法
本章将重叠组稀疏正则项引入二阶广义全变分模型,从而充分挖掘图像梯度的局部组稀疏先验,提高对图像高阶梯度局部结构相似性的刻画能力,然后在带重启加速ADMM框架下,将复杂问题分解成几个解耦合的子问题求解,并加速算法收敛。
2.1 TGV-OGS模型
将重叠组稀疏的约束项来替换TGV模型中L1约束项,改进的TGV-OGS数学模型如式(7)所示:

(7)
式(7)中,TGV2-OGS(F)表示基于重叠组稀疏的二阶广义全变分约束项。
2.2 TGV-OGS模型的ADMM求解
为求解式(7)定义的改进TGV模型,利用ADMM框架对模型进行求解,该方法通过引入去耦合的分裂变量,从而将复杂问题转化为若干个简单的子问题进行求解。分裂变量定义为Z1=Kh*F-Vx,Z2=Κv*F-Vy,Z3=Kh*Vx,Z4=Kv*Vy,Z5=Kv*Vx+Κh*Vy。
将原问题转化为如下问题:
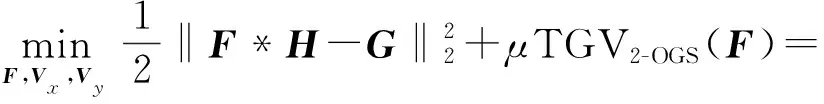
(8)
将式(8)转化为增广拉格朗日函数形式:

(9)
式(9)中,μ1=μα1,μ2=μα2,μ3=μα3,μ4=μα4,μ5=μα5,Λi(i=1,2,3,…,5)是拉格朗日乘子(也称为Ζi(i=1,2,3,…,5)的对偶变量)。〈X,Y〉表示两个矩阵X,Y的内积。
2.2.1F,Vx,Vy子问题求解
在ADMM框架下,分离变量及其对偶变量之间和三元组F,Vx,Vy是去耦合的。
对于F子问题,其子目标函数为:
(10)
利用快速傅里叶变换进行卷积计算式(10)。将式(10)转换为频域表达式得:
(11)
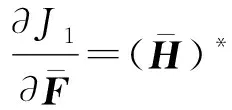
(12)
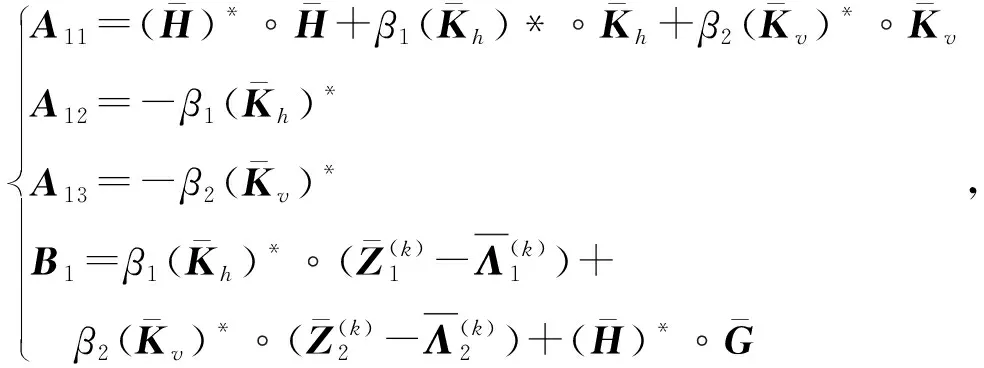
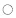
(13)
对于Vx子问题,子目标函数为:
(14)
同理,将式(14)转换为频域表达式得:
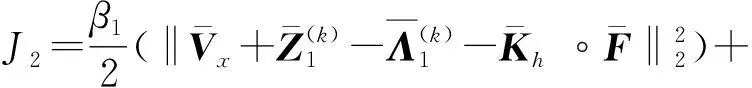
(15)

(16)
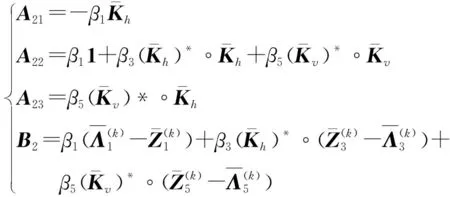
整理得:
(17)
对于Vy子问题,其子目标函数为:
(18)
将式(18)转换为频域表达式得:
(19)


(20)
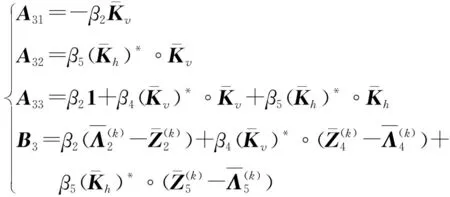
整理得:
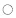
(21)
综合式(13)、式(17)、式(21)得到关于F、Vx、Vy三个变量的方程组,也即:
(22)
利用克莱姆(Cramer)法则与快速反傅里叶变换对F、Vx、Vy分别求解,即:
(23)
2.2.2Zi(i=1,2,…,5)子问题
对于Z1子问题,其目标子函数为:
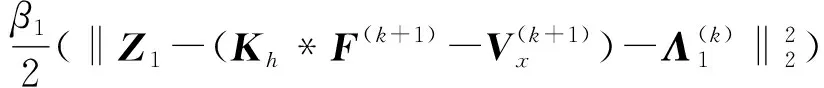
(24)
根据式(3)和式(5),可以得到Z1的更新公式为:
(25)
同理,Zi(i=2,3,…,5)的更新公式为:
(26)
2.2.3Λi(i=1,2,…,5)子问题
Z1的对偶变量为Λ1,其目标子函数为:
(27)
可以利用梯度上升法得其更新公式为:
(28)
式(28)中,γ为学习率。
同理,变量Λi(i=2,3,…,5)的更新如式(29)所示:
(29)
2.3 TGV-OGS模型的带重启加速ADMM求解
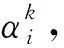
(30)
Zi(i=1,2,…,5)子问题的更新公式如下:
(31)
根据加速ADMM算法框架,Λi(i=1,2,…,5)子问题的更新公式如下:
(32)
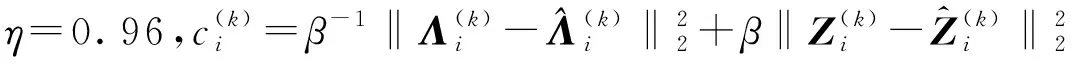
(33)
若重启算法,将下列变量重置:
算法1为所提出模型的求解流程。
算法1 带重启加速ADMM框架下的TGV-OGS去模糊算法。
Input:观测图像G,模糊核H。
Output: 去模糊图像F。
Initialize:
tol,Max(i=1,2,…,5).
1) While‖F(k+1)-F(k)‖2/‖F(k)‖2>tol do
2)B1,B2,B3按式(30)计算;
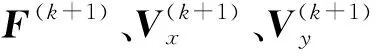
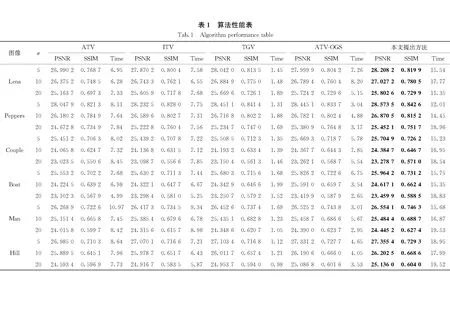
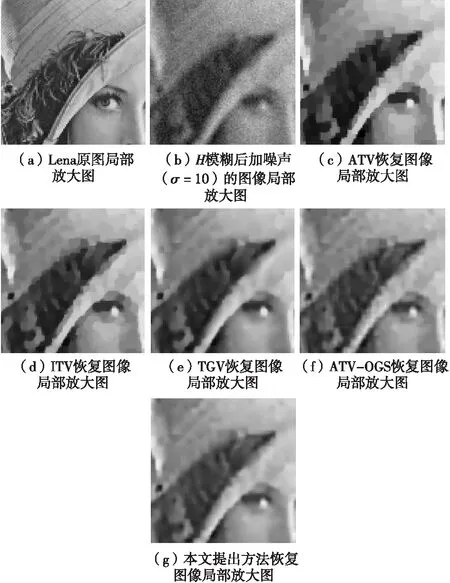
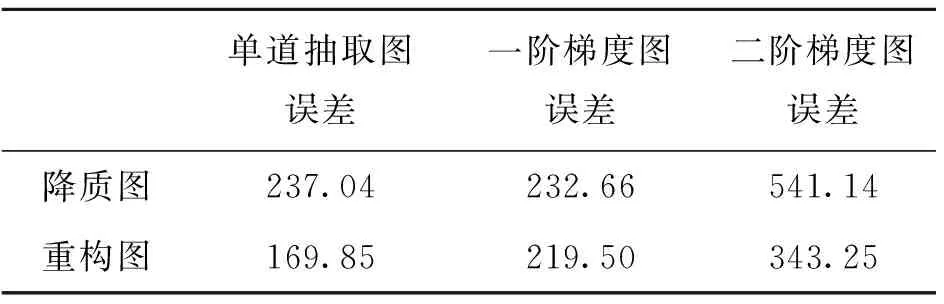
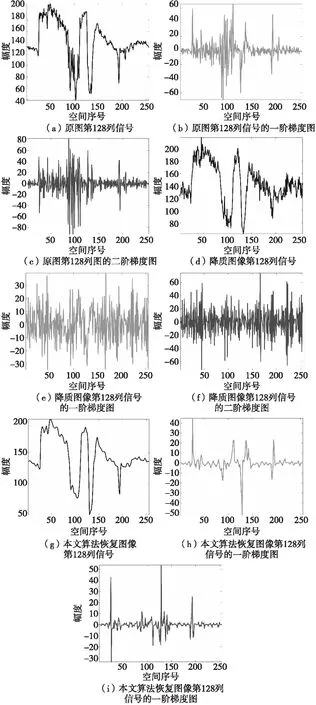
4) Whilen 7)n=n+1; 8) End While 13) Else 15) End if 16)k=k+1; 17) End While 18) ReturnF(k)asF。 本文选取了6幅图进行实验,如图1所示。每幅图像大小为256×256。 图1 测试图像Fig.1 Test images 实验中使用的噪声为高斯随机白噪声。在算法中,模糊核通过psf2otf(point spread punction to optical transform function)点扩散函数来构造,模糊类型为高斯模糊,模糊核大小为5×5,模糊核的标准差为5(利用Matlab指令fspecial('gaussian', [5 5], 5)产生)。实验中,模糊核保持固定不变,将噪声标准差σ分别设置为5、10、20。 本文涉及实验主要对比参数为:峰值信噪比(peak signal-to-noise ratio,PSNR)[5]和结构相似性信息(structural similarity,SSIM)[14]。 以图1为实验测试图像,将提出算法与各向异性全变分(anisotropic total variation,ATV)[15]去模糊方法、各向同性全变分(isotropic total variation,ITV)[16]去模糊方法、TGV[2]去模糊方法及基于重叠组稀疏的各向同性全变分(anisotropic total variation based on overlapping group sparsity,ATV-OGS)[17]去模糊方法进行对比。各比对算法去模糊指标如表1所示。表中黑色粗体标出的指标表示最优图像恢复指标。表1显示,本文提出方法得到的PSNR值和SSIM值均高于其他几种比对方法,说明图像去模糊性能最佳。但是,由于本文提出模型较为复杂,运算速度在比对算法中最慢。 图2和图3分别展示了Lena降质图像的去模糊整体结果和局部放大结果。 图2 Lena五种算法恢复对比图Fig.2 Recovered image comparison 图3 Lena五种算法恢复图的局部放大图Fig.3 Recovered image comparison 图2中,模糊核如图2(c)所示,模糊后的图像被高斯白噪声(σ=10)进一步污染。观察图3可知,本文提出方法相比于其他方法更好地压制了阶梯效应。 图4反映了算法对图像一阶梯度和二阶梯度的约束效果,从图中可以看到,本文提出方法有效压制了受污染图像一阶和二阶梯度的噪声,并保留了原图像一阶、二阶梯度中的最大值,从而较好地恢复出图像。对比图4(a)、(d)、(g)可以发现,该方法有效地去除了尖峰和毛刺,恢复出来的图像去模糊效果相比其他去模糊方法得到了一定程度提升。 表2将图4(d)、(e)、(f)和图4(g)、(h)、(i)关于图4(a)、(b)、(c)的误差进行对比。从表中可以看到,提出方法的单道抽取图、抽取图的一阶梯度和二阶梯度误差均小于污染图像三条曲线关于原图三条曲线的中心误差。 表2 误差对比Tab.2 Error contrast 图4 单道对比图Fig.4 Single signal comparison 图5反映了迭代过程中,恢复图像的相对误差(relative error,RE)变化趋势,其中RE=‖F(k)-F‖2/‖F‖2,F表示原图像,F(k)表示算法恢复图像。从图中可以看到,随着算法不断迭代,恢复图像和原图的误差逐步减小,且算法收敛得非常迅速,在第5次迭代以后,RE曲线就趋于平缓。 图5 算法动态迭代图Fig.5 Dynamic iteration image 本文提出了基于重叠组稀疏收缩技术的改进广义全变分模型去模糊方法。该方法能更充分地挖掘图像一阶和二阶梯度的邻域结构相似性,从而进一步提升了TGV模型的性能。实验结果表明,该方法能有效抑制恢复图像中的阶梯效应,提高对图像高阶梯度局部结构相似性的刻画能力,从而提高图像去模糊效果。数值计算方面,利用带加速重启的交替乘子迭代法求解提出模型,有效提高算法效率。实验结果表明,提出方法的图像重构质量在所有比对算法中达到最佳效果,且算法在迭代少数步数后快速收敛。值得注意的是,本文提出方法也存在一定的局限性,本文算法复杂度较高,在实时处理图像方面存在不足。 本文所提出的正则项可应用于椒盐噪声、指数噪声、柯西噪声等其他噪声背景下图像的去模糊问题,我们将在未来的工作中进一步讨论。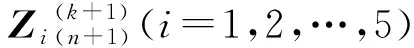
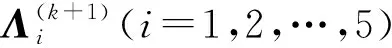
3 实验与分析
3.1 实验说明

3.2 算法性能对比


4 结论

