信道突变对正交调制传输性能影响的分析方法

刘建成，郝学坤，王赛宇，王 超，姜少飞

(1. 中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.中国电子科技集团公司第五十研究所，上海 200331；3. 解放军31634部队，云南 昆明 611731)

0 引言

无线通信是信息时代实现全时全区域消息传输必不可少的通信方式，其传输信道包括空中无线电磁波传输通道和收发信机前端射频有线传输通道，而自然环境和射频器件不确定性对信息的有效、可靠传输造成了严重影响。其中，以卫星通信、深空探测等最为突出，比如电离层闪烁[1]、太阳黑子[2]和核爆[3]等均会引起空中传输信道的突变，而前端射频器件的非理想特性也会引起信号的非线性畸变[4-5]。

针对信道畸变失真问题，学者们近些年开展了大量深入的研究，主要集中于射频非线性预失真处理和空中传输信道特性分析等。文献[4]首先是分析了射频前端非线性，建立对应的数学模型，进而分析了其对大规模MIMO系统上行传输链路传输速率的影响。文献[5]针对5G的大规模MIMO系统发射终端，研究了其射频前端非线性特性及对该系统的影响，以消除射频前端非线性产生的干扰。文献[6]研究了发送端功率放大器非线性的数字预失真补偿方法，预失真以时延线构成的网络结构为基础，使得发送信号较好地抑制了非线性。文献[7]基于瑞利衰落信道，分析了功放非线性消除对MIMO MC-CDMA系统的影响。文献[8]以卫星通信为对象，研究了除功放非线性失真外的传输信道幅频特性和群延迟特性，并进行了基本仿真，为卫星通信传输信道分析提供了参考。文献[9—10]研究了CDMA系统受传输信道非线性失真的影响，利用非线性器件的AM-AM和AM-PM特性预测发送信号的邻道功率抑制比(ACPR)、噪声功率比和二阶交调乘积，为提升CDMA发送信号特性奠定了基础。文献[11]针对OFDMA上行链路的FBMC/OQAM传输信号，从接收端角度出发，分析了强频率选择性和定时误差情况下的非线性失真问题，给出了子载波数目足够大时的脉冲非线性表达式。文献[12]针对发送端功率放大器非线性补偿消除问题，分析了发送端预失真、接收端均衡和码间串扰消除等技术方法，表明判断反馈均衡与非递归结构均衡相比并无明显提升。除此之外，文献[13]研究了信号畸变对卫星导航测距的影响，利用大口径天线接收、高性能滤波和多周期伪码平均等措施恢复发送信号，指出导航信号畸变将带来较大的测距误差。

由上述分析可知，有效分析传输信道不确定性、外界环境和射频器件等突变易对卫星通信链路产生的严重影响，是提升系统应对能力的前提基础。针对该问题，本文提出了信道突变对正交调制信号传输性能影响的分析方法，提供了有力的理论和仿真数据支撑。

1 信道突变下正交调制信号数学描述

数字通信因其传输速率与纠错能力可控，成为目前卫星通信的主要方式，而正交调制又是数字通信中采用最多的0、1比特映射形式，其中以QPSK和QAM应用最为广泛，二者具有实现简单、抗噪性能强等优势，但其信号非恒包络，通过无线和射频通道时易产生非线性失真，对信道突变较为敏感。以π/4QPSK调制和矩形16QAM为例，信号矢量表示分别如图1(a)和(b)所示，其中矢量s表示无失真的调制信号矢量，矢量s′表示突变后对应的信号矢量。对于QPSK调制，只有信号矢量的角度承载了传输的信息，而对于16QAM调制，幅度和角度共同承载了传输的信息。

图1 正交调制信号矢量示意图Fig.1 Vector diagram of quadrature modulation signal

信道突变时可导致信号矢量发生由s至s′的变化，由此我们可进一步将信道异常时刻的信号畸变等价于其幅度陡降、相位突变和频偏突变。对于QPSK和QAM等正交调制信号，其基带信号的复数形式可表示为：s(n)=I(n)+jQ(n)，其中I(n)为同相分量，Q(n)为正交分量，j表示复数算子(j2=-1)。不妨设s(n)的强度归一化，即正交调制信号矢量s幅度的均值为1。假设异常突变所导致的幅度陡降为β(无陡降时β=1，β越小表示陡降越严重)，相位突变为φ，频偏差异为fΔ，则异常时刻的QPSK和16QAM调制基带信号s′(n)均可表示为：

s′(n)=β·s(n)ej(2πfΔnTs+θ+φ)

(1)

式(1)中，Ts表示调制信号的符号周期，θ表示频偏差异的初始相位，为便于分析，可令：

φ′=θ+φ

(2)

在式(2)基础上，则s′(n)可进一步表示为：

s′(n)=I′(n)+jQ′(n)=βI(n)cos (2πfΔnTs+φ′)-
βQ(n)sin (2πfΔnTs+φ′)+
j[βQ(n)cos (2πfΔnTs+φ′)+
βI(n)sin (2πfΔnTs+φ′)]

(3)

由式(3)可见，在信道突变时，正交调制信号的I和Q路均会产生明显失真，且与三个变化参量均有关系。

2 分析方法

信道突变造成的信号失真如何影响信号质量和系统传输性能是我们最关注的，为此本节提出基于信号EVM和系统误码率Pe的分析方法，研究信号三个变化参量与二者之间的关系，并推导数学闭合表达式，为后续分析提供有力的理论支撑。由于QPSK和16QAM应用较为广泛且具有代表性，故本节仍以二者为例进行分析，其具体方法和推导过程可适用于其他正交调制方式。

2.1 突变对EVM影响的分析

根据式(3)可计算，QPSK和16QAM调制信号s(n)与s′(n)之间差异为：

(4)

令：

θn=2πfΔnTs+φ′

(5)

进一步整理可得：

e(n)=I2(n)+Q2(n)+
β2[I(n)cos (θn)-Q(n)sin (θn)]2+
β2[Q(n)cos (θn)+I(n)sin (θn)]2-
2I(n)β[I(n)cos (θn)-Q(n)sin (θn)]-
2Q(n)β[Q(n)cos (θn)+I(n)sin (θn)]

(6)

e(n)=I2(n)+Q2(n)+
[I2(n)+Q2(n)]β2[cos2(θn)+sin2(θn)]-
2β2I(n)cos (θn)Q(n)sin (θn)+
2β2I(n)cos (θn)Q(n)sin (θn)-
2βI2(n)cos (θn)+2βI(n)Q(n)sin (θn)-
2βQ2(n)cos (θn)-2βI(n)Q(n)sin (θn)

(7)

e(n)=I2(n)+Q2(n)+
β2[I2(n)+Q2(n)]·[cos2(θn)+sin2(θn)]-
2βcos (θn)[I2(n)+Q2(n)]=
[I2(n)+Q2(n)][1-2βcos (θn)+β2]

(8)

由式(8)可得异常突变时刻的QPSK和16QAM信号EVM表达式如下：

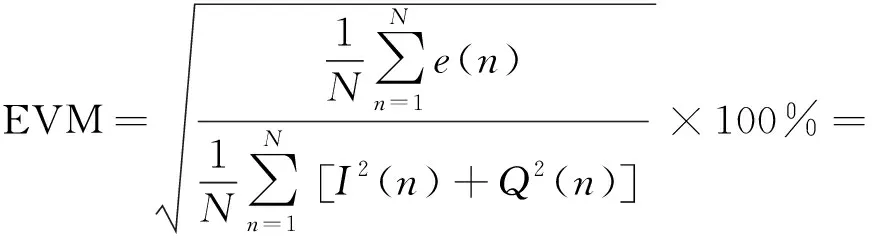
(9)

在信号强度归一化情况下，对于QPSK信号有I2(n)+Q2(n)=1，将式(2)和式(5)代入式(9)，可得突变时刻幅度陡降为β，相位突变为φ，频偏差异为fΔ与QPSK信号EVM之间的数学闭合关系式，如式(10)所示：

(10)

对于16QAM调制，当信号强度归一化时，I2(n)+Q2(n)取值为1/5、1和9/5三种情况，且三种取值出现概率分别为0.25、0.5和0.25。所以，当符号个数N足够大时，可得16QAM信号EVM与幅度陡降β，相位突变φ和频偏差异为fΔ之间的数学闭合关系式：

(11)

分析式(10)和式(11)可见，QPSK和16QAM调制信号EVM值具有相同表达式，与幅度陡降、相位突变以及频偏差异都息息相关，若信号无陡降即β=1，相位无突变φ=0，频偏差异fΔ为0，则理论计算的EVM值为0，与实际相符。当信号存在突变时，随着陡降的加剧EVM值会随之增大，当陡降一定时EVM值也会随着相位突变和频率偏移的变化而增大。

2.2 突变对系统误码率Pe影响的分析

除信号EVM值之外，系统误码率也是反映突变影响的另一个重要指标。为便于分析，假设QPSK和16QAM信号畸变未发生在同步符号传输的时刻，并不影响系统同步定时性能。

对于QPSK和16QAM调制，无突变时系统接收基带信号r(n)均可表示为：

r(n)=s(n)+ε(n)=
I(n)+jQ(n)+εi(n)+jεq(n)

(12)

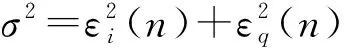
(13)

式(13)中，Es表示符号能量，n0表示符号周期对应的噪声强度，该式中大小等于σ2。

由于突变引起的幅度陡降、相位突变和频偏差异具有随机性，在系统接收端表现出信息符号采样值的无规律变化，近似于接收符号上叠加了系统噪声，所以分析系统误码率变化的核心是推导信号突变对信噪比的恶化。参考突变信号表达式(3)，突变后的接收信号表示为：

r′(n)=s′(n)+ε(n)

(14)

此时接收信号的信噪比等价计算为：

(15)

进一步推导，可得：

(16)

(17)

利用式(5)化简可得：

(18)

所以，由信号瞬时突变引起的系统接收端信噪比恶化可由信噪比差值体现，表达式为：

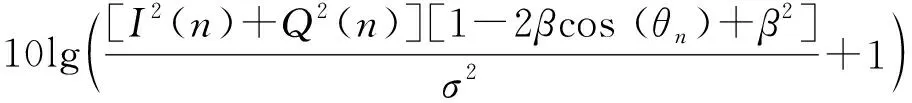
(19)

在式(18)基础上可得突变情况下，将信噪比数值由dB转换为比值，可得QPSK调制系统接收端误码率公式表示如下：

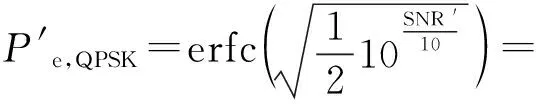
(20)

式(20)中，I2(n)+Q2(n)为原信号强度，通常情况下可将其归一化，则系统误码率变为：

(21)

同理，将信道突变后16QAM信号的信噪比代入其误码率表达式，具体可参考文献[14]，即可求得信道突变时所对应的系统误码率。

可见，幅度陡降越严重，即越β取值越小，相位突变量θn越大，则误码率将越大，所以幅度陡降和相位变化共同决定了信道突变对系统误码率的恶化程度。另外，式(19)所示的有无瞬时变化所对应的接收端信噪比差值也可反映出系统性能，即差值越大表示系统性能恶化越严重，对应的是幅度陡降、相位突变和频偏差异的增加。

3 实验仿真

在上述理论推导基础上，通过实验和仿真进一步分析信道畸变对正交调制传输的影响。利用课题组现有的卫星通信收发终端和仪器，搭建如图2所示的卫星通信正交调制传输链路实验环境。利用外围电路实验环境中的功率放大器，模拟传输信道的突变。以QPSK信号为例，通过矢量分析仪在突变前后观测的信号EVM和星座图如图3所示。

图2 信道突变测试环境Fig.2 Channel break test environment

图3 突变前后信号EVM和星座图对比Fig.3 Comparison of signal EVM and constellation before and after channel break

由图3所示测试结果可知，QPSK信号EVM测量值在信道突变前由于噪声影响约为25%，而伴随信道突变其大小突然猛增，高达95%以上；QPSK信号星座图突变前虽然因噪声影响略有扩散，但仍相对集中于四个象限，而当传输信道发生突变时，星座图发生严重的弥散，随机分布在四个象限，已无法区分判决。可见，当无线通道或者射频通道发生突变，QPSK信号的EVM和星座图将发生显著的失真，进而恶化了其传输性能。

为进一步量化分析信道突变对正交调制传输性能影响，建立仿真模型，通过蒙特卡洛仿真统计不同突变情况下对应的系统误码率。由式(5)和2.2节分析可知突变产生的频率差异与相位变化可相互转换，故仿真设置不同的陡降比η和相位突变为φ两个变量，统计分析信道突变对QPSK和16QAM调制EVM与系统误码率的影响，其中幅度陡降比η由β计算得出，关系为η=(1-β)×100%。同时引入突变出现周期Tp和持续时间td两个参数，信道突变周期表示在时间Tp内随机出现一次信道突变，持续时间为td。仿真环境设置基于以QPSK和16QAM调制为主的卫星通信传输链路，其传输信道多径效应较弱，通常可近似为白噪声信道，设定的信道突变条件下链路参数如表1所示。

表1 QPSK、矩形16QAM调制的链路仿真参数Tab.1 Simulation parameters of QPSK and 16QAM

为分析信道突变对信号EVM值的影响，设定传输信道比特信噪比Eb/N0为12 dB，无信道突变对应的接收端信号EVM值为25.01%，对于不同的幅度陡降比和相位突变对应的信号EVM仿真和理论计算值如表2所示。对比由式(10)和式(11)计算的理论值和统计平均的仿真值可见，仿真结果与理论分析相吻合，对比分析不同参数所对应的信号EVM仿真和理论值变化，进而可知信道突变对链路传输性能的恶化程度。

表2 信道突变对应的信号EVM值Tab.2 Signal EVM value corresponding to channel break

为直观反映信道突变对链路传输性能的影响，设定QPSK和16QAM调制链路比特信噪比分别为6 dB和9 dB，单位时间内有多次信道突变，每次持续时间相同，具体参数设置同表1。统计平均1 000次蒙特卡洛仿真结果，QPSK和16QAM调制链路对应的误码率变化分别如图4和图5所示。

由图4和图5所示的信道突变情况下链路传输误码率结果可见，信道突变将会严重恶化QPSK和16QAM链路的传输性能。以仿真条件中设定的信道突变条件为例，当幅度陡降比为30%，相位突变为10°，由图4(a)和图5(a)可知QPSK和16QAM传输链路误码率均约为10-5，此时链路传输可靠性还能满足大部分应用；而当幅度陡降比增加至50%，相位突变为20°时，QPSK链路传输误码率恶化约为0.004，16QAM链路传输误码率约为0.008，已无法保证信息的可靠传输。另外，分析图4(a)和图5(a)误码率曲线变化趋势，表明无论信道突变是否导致相位突变，只要幅度陡降超过30%则会严重恶化QPSK和16QAM链路传输性能，分析图4(b)和图5(b)可知对于相位突变大于20°时，即使幅度陡降比较小也会造成QPSK和16QAM链路传输性能的严重恶化。

图4 QPSK调制链路受信道突变影响的误码率变化曲线Fig.4 Variation curve of BER of QPSK modulation link affected by channel break

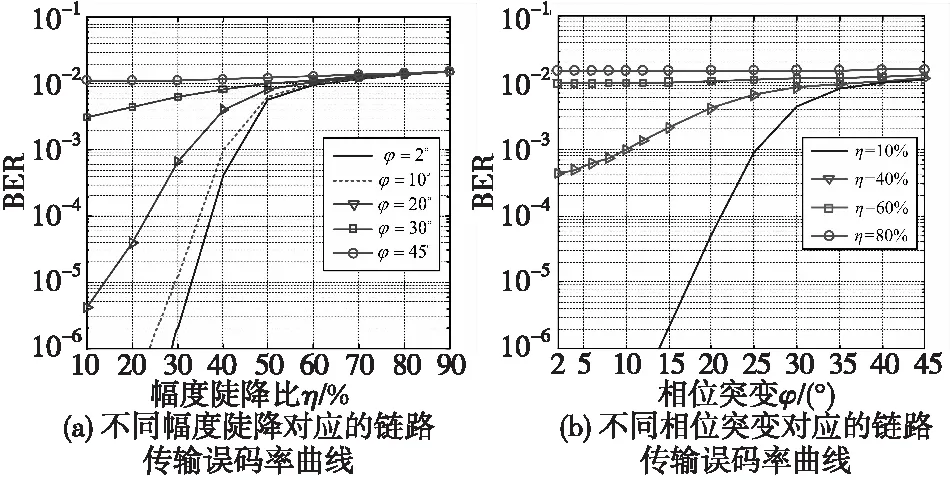
图5 不同相位突变对应的链路传输误码率曲线Fig.5 BERcurves of transmission link corresponding to different phase break

综上所述，对于QPSK和16QAM链路面临信道突变，将严重影响信号EVM值大小，从而显著增加链路传输的误码率，恶化链路传输性能。通过理论和上述仿真分析，可为实际信道突变环境的正交调制传输性能分析提供重要的参考依据。

4 结论

本文提出了信道突变对正交调制信号传输性能影响的分析方法。该方法以QPSK和16QAM等典型正交调制信号为对象，首先建立信道突变时刻对应的信号数学模型，推导得出幅度陡降、相位突变与信号EVM值、信号SNR之间的闭合数学关系式，进而计算对应的系统误码率。仿真实验和理论计算结果表明，幅度陡降高于50%、相位突变大于20°均会严重恶化链路传输性能，误码率逼近10-2，为传输系统有效应对信道突变提供了有力的理论依据和支撑。